Today's Topic
集合\(A\)が集合\(B\)の部分集合であることを示すためには、
$$x \in A ならば x \in B$$
であることを示せば良い。
2つの集合\(A, B\)が等しいことを示すためには、
- 全ての要素を書き上げ、全て一致していることを示す
- \(A \subset B\)かつ\(A \supset B \)であることを示す
のどちらかができればOK(どっちも同じ意味)



この記事を読むと、この問題が解ける!
- 集合\(\left\{a, b, c\right\}\)の部分集合を全てかき出せ。
- 次の2つの集合は等しいか調べよ。
$$A = \left\{ x| xは12の正の約数 \right\}$$
$$B = \left\{ 1, 2, 3, 4, 6, 12\right\}$$

包括関係と部分集合
次のような2つの集合を考えてみましょう。
$$ B = \left\{ 1, 2, 3, 4, 5, 6 \right\} $$
このとき、集合\(A\)に含まれる全ての要素は、集合\(B\)に含まれています。

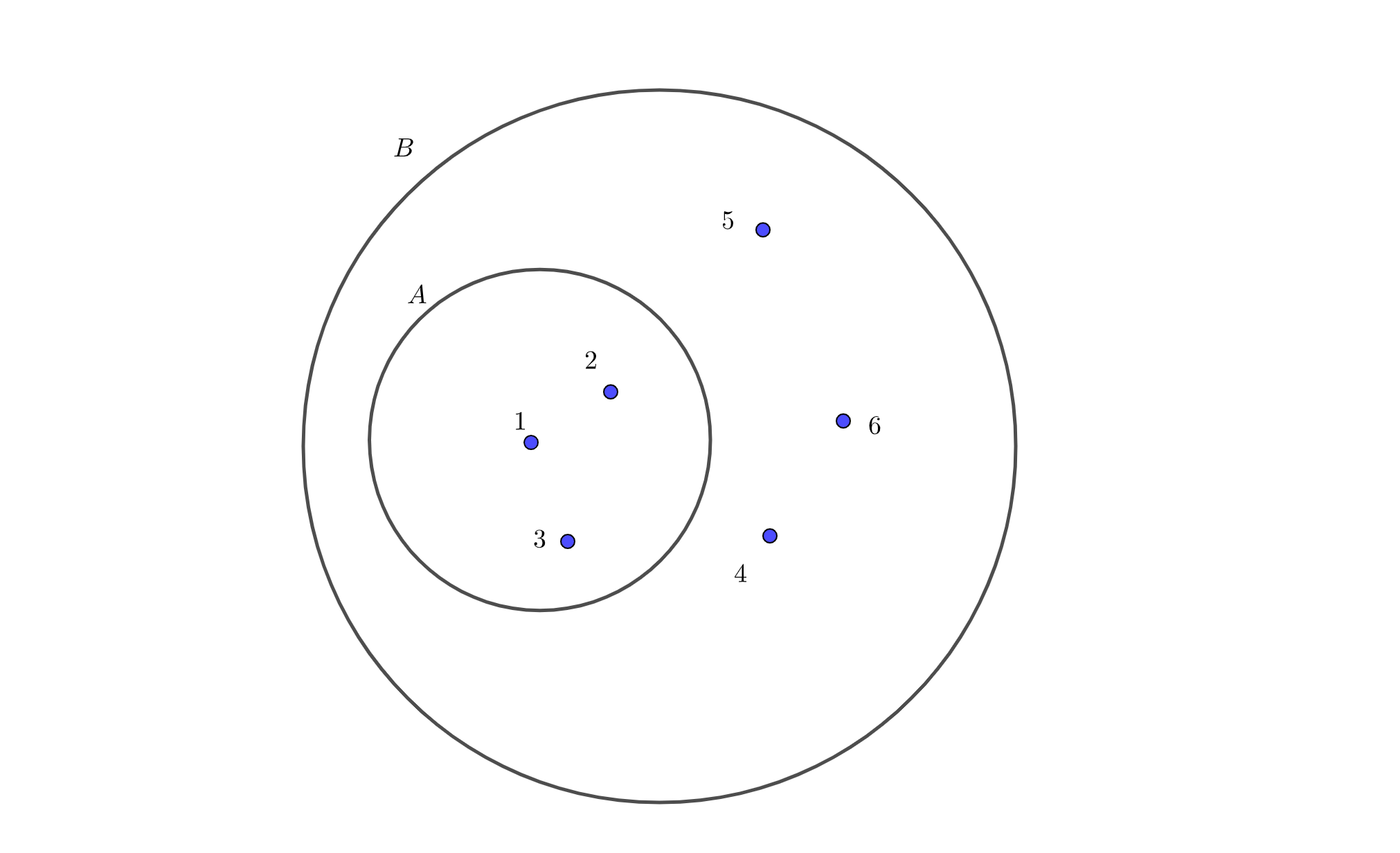
ベン図を見てみるとわかるとおり、集合\(B\)は集合\(A\)そのものを含んでいるように見えます。
ポイント
このように集合\(A\)の全ての要素を、集合\(B\)が含んでいる場合、
- \(A\)は\(B\)の部分集合
- \(B\)は\(A\)を含む
といい、\(A \subset B\)のように書きます。


すなわち、
ポイント
集合\(A\)が集合\(B\)の部分集合(\(A \subset B\))であることを示すためには、
$$x \in A ならば x \in B$$
であることを示す
必要があるということですね。
自分も部分集合!
ある集合\(A\)の部分集合を考えるとき、念頭に置いておいて欲しいのは、\(A\)自身も部分集合としてカウントされるということ。
そのため、常に
が成り立ちます。
空集合
ここで、1つ特殊な集合をご紹介しましょう。
これまで考えてきた集合は、少なくとも1つの要素を持っているものばかりでした。
しかし、「たったの1つも要素を持たない集合」というのも存在します。
それが空集合です。
空集合は\(\phi\)(ファイ)で表す習慣があり、どんな集合に対しても必ず部分集合になるという定義がされています。
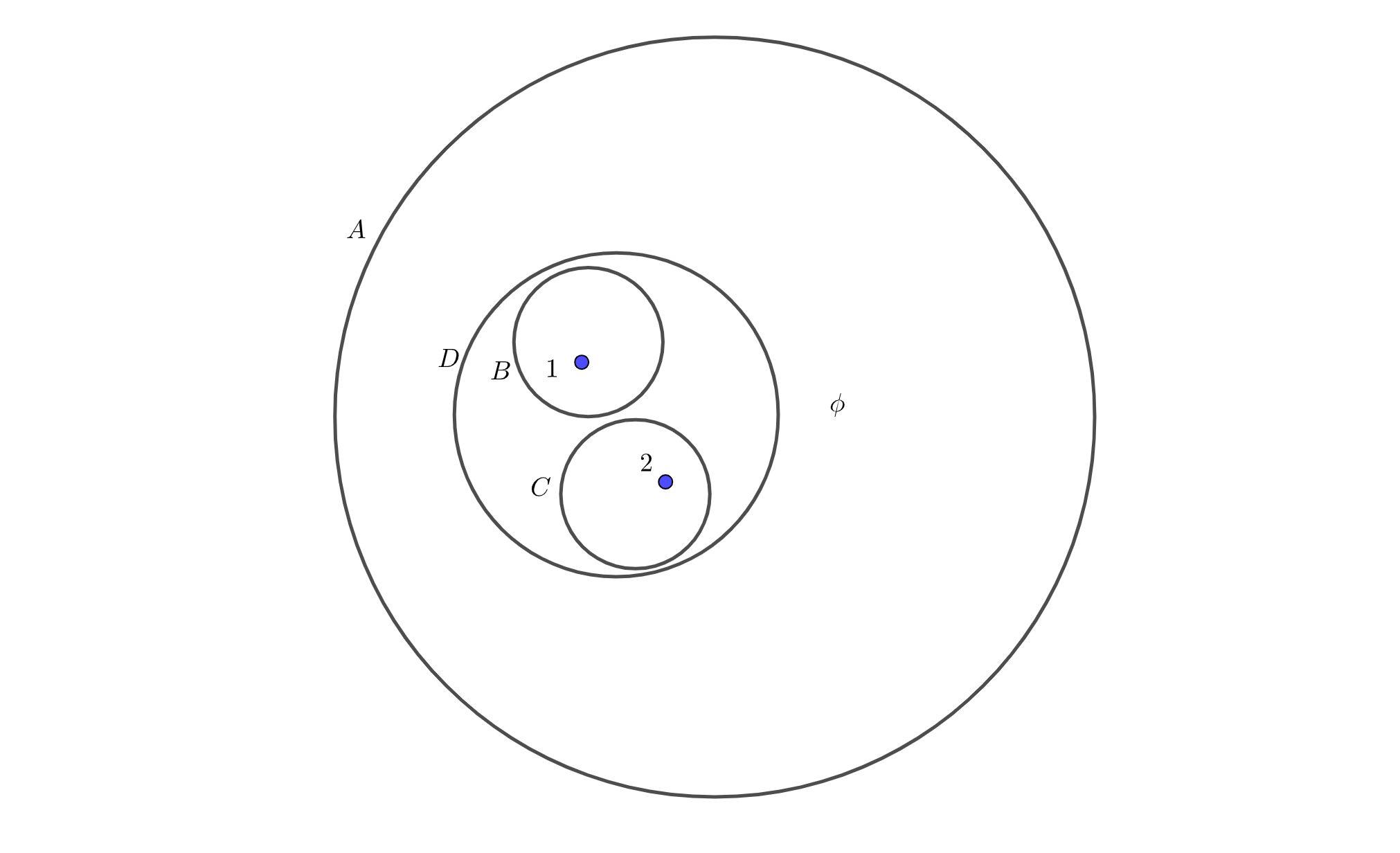
例えばある集合\(A = \left\{ 1, 2 \right\}\)は、
$$C = \left\{ 2 \right\}$$
$$D = \left\{ 1, 2 \right\}$$
$$\phi$$
と、計4つの部分集合を含んでいることになります。

等しい集合とは
2つの集合\(A\)と\(B\)に関して、全ての要素が一致している場合、集合\(A\)と\(B\)は等しいとなります。
2つの集合が等しいことを示すためには、次の2通りがあります。
- 2つの集合の要素を書き上げ、全てが一致していることを示す
- \(A \subset B\)かつ\(A \supset B\)を示す
それぞれ例題を見てみましょう。
全ての要素が一致している
2つの集合が等しいとは、全ての要素が共通であることをいいましたね。
なので、それさえ証明できれば2つの集合が等しいことは認められます。
例題
次の2つの集合\(A, B\)が等しいことを証明せよ。
$$A = \left\{ x | 0以上10未満の奇数 \right\}$$
$$B = \left\{ 2x-1 |xは 0 < x < 6 を満たす整数 \right\}$$
(※見切れている場合はスクロール)
集合\(A\)の全要素は、
集合\(B\)の全要素は、
よって\(A, B\)の全ての要素が互いに一致しているので、\(A=B\)。
互いに包括している
ある集合\(A\)は、部分集合に自分自身も含めるため、\(A \subset A\)が成り立つのでしたね。
そのため\(A = \left\{ 1,2 \right\}\)であれば、その部分集合に\(\left\{ 1,2 \right\}\)を持っているということになります。
これを念頭に、上記の全ての要素が一致している2つの集合\(A\)と\(B\)について考えてみましょう。
$$B = \left\{ 1, 3, 5, 7, 9 \right\}$$
このとき、
- 右辺だけ見ると、全く同じ集合である
- 集合は、自分自身も部分集合としてカウントする
という点から、\(A \subset B\)かつ\(A \supset B \)であることがわかります。
仮に
みたいな集合だと、\(A \subset B\)は成り立つけど、\(A \supset B \)は成り立ちませんね?
よって等しい2つの集合であれば、\(A \subset B\)かつ\(A \supset B \)が成り立つということになります。


まとめ

まとめ
集合\(A\)が集合\(B\)の部分集合であることを示すためには、
$$x \in A ならば x \in B$$
であることを示せば良い。
2つの集合\(A, B\)が等しいことを示すためには、
- 全ての要素を書き上げ、全て一致していることを示す
- \(A \subset B\)かつ\(A \supset B \)であることを示す
のどちらかができればOK(どっちも同じ意味)
今回扱った、集合の含む・含まれるというような関係のことを包括関係と言うことがあります。
集合の包括関係は現代数学の基本として鎮座しており、その重要さを無視することはできません。

ここで苦手意識を持たず、乗り越えていってくれれば、きっと数学の楽しさに気づけます。
以上、「集合の包括関係について」でした。
チェック問題
例題
集合\(\left\{a, b, c\right\}\)の部分集合を全てかき出せ。
$$\left\{ b\right\}$$
$$\left\{ c\right\}$$
$$\left\{ a, b\right\}$$
$$\left\{ a, c \right\}$$
$$\left\{ b,c \right\}$$
$$\left\{ a, b, c\right\}$$
$$\left\{ \phi\right\}$$
例題
次の2つの集合は等しいか調べよ。
$$A = \left\{ x| xは12の正の約数 \right\}$$
$$B = \left\{ 1, 2, 3, 4, 6, 12\right\}$$
よって、\(B\)と全ての要素が等しいので








