Today's Topic
$$\lim_{n\rightarrow \infty}\left(1+\frac{1}{n}\right)^n=e$$




こんなあなたへ
「自然対数って何?」
「ネイピア数\(e\)の意味がわからない。何の数よアレ???」
この記事を読むと・・・
- お金の話を使って、感覚的にネイピア数の定義を覚えられる!
- ネイピア数のメリットや、活躍する場面がよくわかる。
指数・対数を一気に理解したい方への記事は、こちらにまとめてあります。
Contents
ネイピア数講座|ネイピア数の定義
まず最初にネイピア数の定義を確認しておきましょう。
ネイピア数の定義
$$\lim_{n\rightarrow \infty}\left(1+\frac{1}{n}\right)^n=e$$
左辺の式によって求められる数を、ネイピア数\(e\)と定義しているわけですね。
ネイピア数\(e\)は\(e=2.7182818\cdots\)と無理数となっていて、万有率と呼ばれることもあります。


ネイピア数(ネイピア数)講座|借金から作られた経緯
皆さんは借金したことありますか?(しないほうがいいよ。)
借金をするとき、借す側は利率というものを上乗せして返してもらいます。
つまり借りる側は、返すときに借りた時よりも多くのお金を払う必要があります。


100万円渡す際に、以下のように契約を交わしました。
1年後に2倍にして返済すること。

このとき「利率は年100%」と言います。
返済期限は1年間なので、
1年後:\(100万円\times(1+1)=2\times100万円\)
にして返す必要があります。
借金はこのように、お金を借すこと自体に付加価値をつけていきます。




複利とは利子がついた金額に、さらに利子が上乗せされることです。
年率100%の半年複利なので、借りてから半年後に50%上乗せした金額を返済し、さらに半年後その返済した金額に50%上乗せした金額を返済する必要があります。
式でわかりやすく書くと、
(※見切れている場合はスクロール)
となります。
1年で100%利子を上乗せして一回返してもらうと2倍ですが、半年で50%の利子を上乗せして2回返してもらうと2.25倍になります。
つまり返済期間を短くするほど、リターンの倍率が増えるというわけです。
参考複利についてはこちらが超わかりやすいです!→知るぽると|複利とは
そこで借金取りの僕は

と欲を丸出しにし始めます。
例えば、年率100%の4ヶ月複利(1年を3分割)の契約を考えてみましょう。
すると、
8ヶ月後:\(\left(100万円\times\left(1+\frac{1}{3}\right)\right)\left(1+\frac{1}{3}\right)=1.777\cdots\times100万円\)
1年後:\(\left(100万円\times\left(1+\frac{1}{3}\right)\right)\left(1+\frac{1}{3}\right)\left(1+\frac{1}{3}\right)=2.37\cdots\times100万円\)
(※見切れている場合はスクロール)
となり、約2.4倍になって返ってきます。


さらにヒートアップして、年率100%の1ヶ月複利(1年を12分割)を試してみましょう。
2ヶ月後:\(\left(100万円\times\left(1+\frac{1}{12}\right)\right)\left(1+\frac{1}{12}\right)=1.173\cdots\times100万円\)
・・・
1年後:\(100万円\times\left(1+\frac{1}{12}\right)^{12}=2.613\cdots\times100万円\)
(※見切れている場合はスクロール)
となり約2.6倍に!
年率100%の1日複利(1年を365分割)にしてみると、
2日後:\(\left(100万円\times\left(1+\frac{1}{365}\right)\right)\left(1+\frac{1}{365}\right)=1.005\cdots\times100万円\)
・・・
1年後:\(100万円\times\left(1+\frac{1}{365}\right)^{365}=2.714\cdots\times100万円\)
(※見切れている場合はスクロール)
となり約2.7倍になりました。


2秒後:\(\left(100万円\times\left(1+\frac{1}{31536000}\right)\right)\left(1+\frac{1}{31536000}\right)=1.000\cdots\times100万円\)
・・・
1年後:\(100万円\times\left(1+\frac{1}{31536000}\right)^{31536000}=2.718\cdots\times100万円\)
(※見切れている場合はスクロール)


確かに複利は細かく返済期限を設けるほど、元金が多くなって返ってきます。
しかし細かくするほど、その倍率の増え方は緩やかになっていき、利益の差もなくなっていきます。

このように、返済期限を細かく設定しまくると、倍率はある一定の値に近づくことが予想されます。
では年率100%の瞬間複利、つまり\(\infty\)で1年を分割したときのリターンは何倍なのでしょうか。
ポイント
$$\lim_{n\rightarrow\infty}\left(1+\frac{1}{n}\right)^n$$
を計算すれば値が得られますが、これこそネイピア数の定義です。

ネイピア数講座|ネイピア数のメリット
この借金取りが超喜びそうなネイピア数ですが、これが高校数学で扱われる理由は皆さんを借金取りにしたいから、ではありません。
実は数学上、かなり便利な性質があります。
自然対数ln
定義
底が\(e\)の対数\(\log_e x\)を自然対数といい、\(\ln x\)と表すこともある。
ネイピア数\(e\)を省いて、\(\log x\)と表すこともあるのですが、常用対数も同様に表すことがあり、ごちゃごちゃになってしまいます。
常用対数について復習したい人はこちらを参考にしてください。
続きを見る

【感覚で理解できる!】常用対数とは?意味と使い方を徹底解説!!
そこでln(log naturalの略)で表すことの方が多い気がします。


この自然対数、何が自然かというと数学の世界では「あ、また出てきた」的なノリで出てくる数だからです。
トキワの森のキャタピーくらい出ます。
中でも自然対数\(\ln x\)を微分すると、\(\frac{1}{x}\)になることはかなり頻繁に使います。
ポイント
$$\left(\ln x\right)'=\frac{1}{x}$$
無限に微分できる\(e^x\)
\(e\)の指数関数\(y=e^x\)は、かなり便利な関数です。
なぜなら何回微分しても値が変わらないからです。
ポイント
\(y=e^x\)とするとき、\(y'=\left(e^x\right)'=e^x\)
証明自体は非常に簡単なので、リミットさえ理解しておけば3秒でわかります。
大事なのはこの微分しても変わらないという性質が、後々かなり便利になるということです。
\(e^x\)の微分について知りたい人はこちらを参考にしてください。
【大学数学】標準正規分布\(\frac{1}{\sqrt{2}}e^{-\frac{x^2}{2}}\)
社会科学や統計学などで度々目にすることになるのが、この正規分布です。
ポイント
平均を\(\mu\)、分散を\(\sigma^2\)とするとき、確率密度関数
$$f(x)=\frac{1}{\sqrt{2\pi\sigma^2}}exp\left(-\frac{\left(x-\mu\right)^2}{2\sigma^2}\right)$$
に従う確率分布を正規分布という。
※\(e^x\)をexp(x)と表すことがある。
この(標準)正規分布のグラフは、図のようになります。
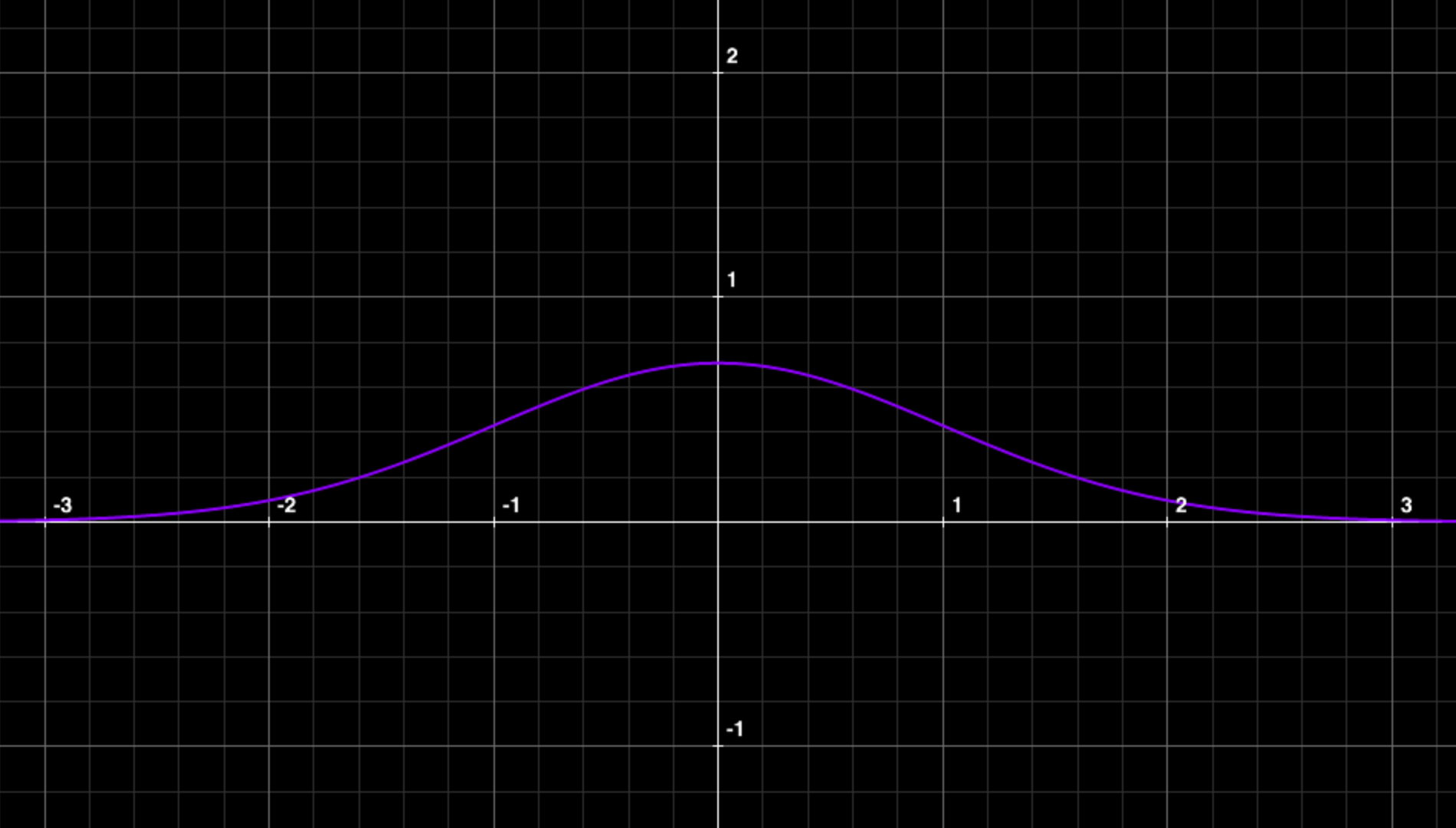

自然界にはこの正規分布に従うものがあり、多数のデータを集約して扱う統計なんかもこれがかなり有用です。
【大学数学】オイラーの公式\(e^{i\pi}=-1\)
数学を極める気がないという人は、ここはすっ飛ばしてください。
理系で数学が好きな方は、大興奮間違いなしの数式がオイラーの公式です。
ポイント
$$e^{i\theta}=\cos\theta + i\sin \theta$$
この記事では証明なんかよりも、この式の美しさに気づいて欲しいです。
まず左辺は自然対数、虚数、そして\(\theta\)という有名な変数たちが指数関数で構成されています。
そして右辺はサインコサインと虚数で構成され、複素数平面を体現してます。
この式は、三角関数と指数関数、そして定数\(e\)と\(\pi\)が複素数の世界では深い関わりがあることを表しているのです。
ネイピア数講座|まとめ
それでは最後にまとめをしておきましょう。
まとめ
- ネイピア数の定義:$$\lim_{n\rightarrow \infty}\left(1+\frac{1}{n}\right)^n=e$$
- 複利計算として考えると、理解しやすくなる。
- 数学の世界ではキャタピーくらい普通に出てくる。
ネイピア数は主に数Ⅲで扱うことが多く、理系学生の人しか馴染みがないかもしれません。
ですがこの世の中で定義されている定数について理解を深めておくことは、あなたにとってもかなり有用な知識となるはずです。
またちょっとだけ紹介した標準正規分布は、文系の方でも学ぶ機会がいくらでもある統計学でも、かなり重要なポジションにあるものだということだけは忘れないでくださいね。
以上、「ネイピア数について」でした。






