Today's Topic
対数関数\(y=\log_a x\)は、
- 指数関数に直して考えるとわかりやすい。
- 底\(a\)が1以下の小数か、1以上か場合分けして考える。
- 底の値によらず、必ず点\((1,0)\)を通る。
- \(y\)軸を漸近線にもつ。
- 指数関数とは、逆関数の関係にある。
- \(x\)が増えても、\(y\)の値がほとんど増えない。




この記事を読むと、この意味がわかる!
- 対数関数の基本性質
- 指数関数との関係性
Contents
対数関数のグラフ
対数関数\(y=\log_a x\)は、指数関数をベースに考えています。
そしてその指数関数は、便宜上
\(0<a<1\)もしくは、\(1<a\)のときのみ考える
ため、対数関数も同様に、\(0<a<1\)もしくは、\(1<a\)のときのみを考えます。

加えて、対数と指数の関係を考えると
\(y=\log_a x \iff a^y = x\)
であることから、\(x\)は正の値しか取りません。


以上、対数関数\(y=\log_a x\)において
- 底\(a\)は\(0.〜\)もしくは、1以上の値
- 真数\(x\)は負の値にはならない→第1、第4象限だけにグラフが描ける
という2点に注意すると、対数関数のグラフは場合分けにより
- 底が0.〜のとき
- 底が1より大きい数のとき
の2つ描けることがわかります。

\(0<a<1\)のとき
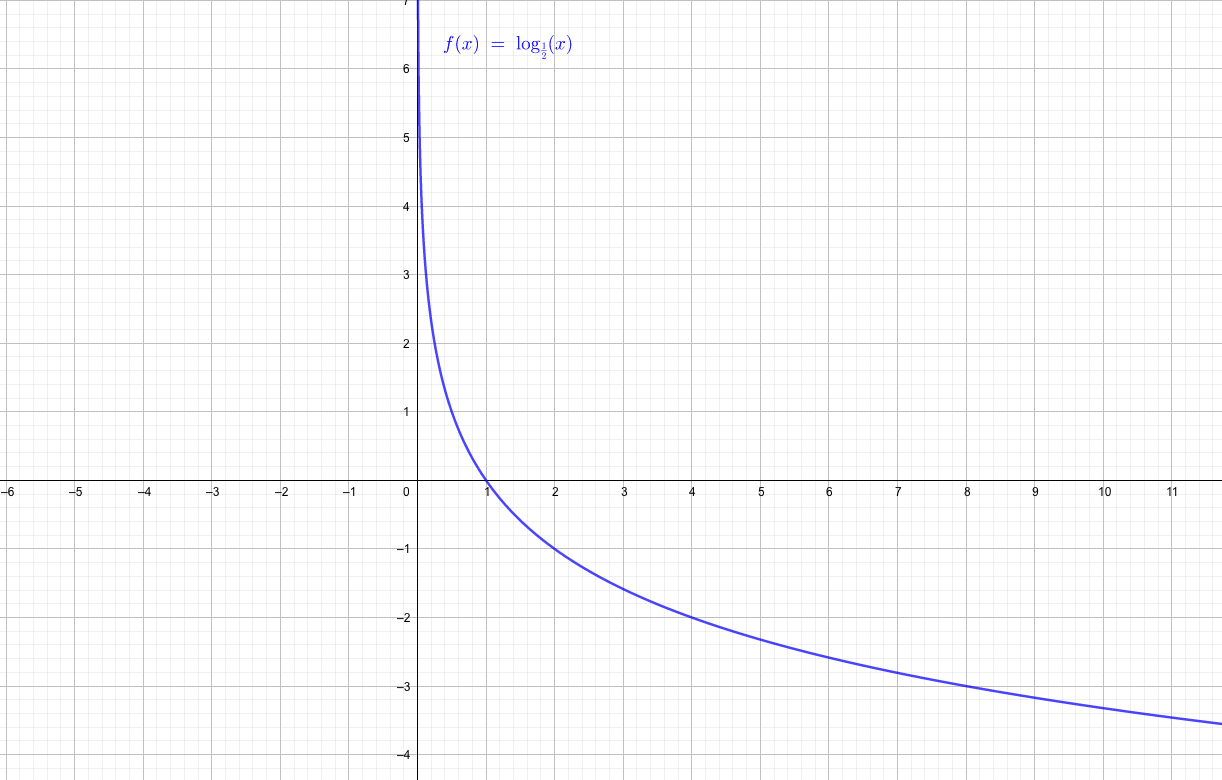

\(1<a\)のとき
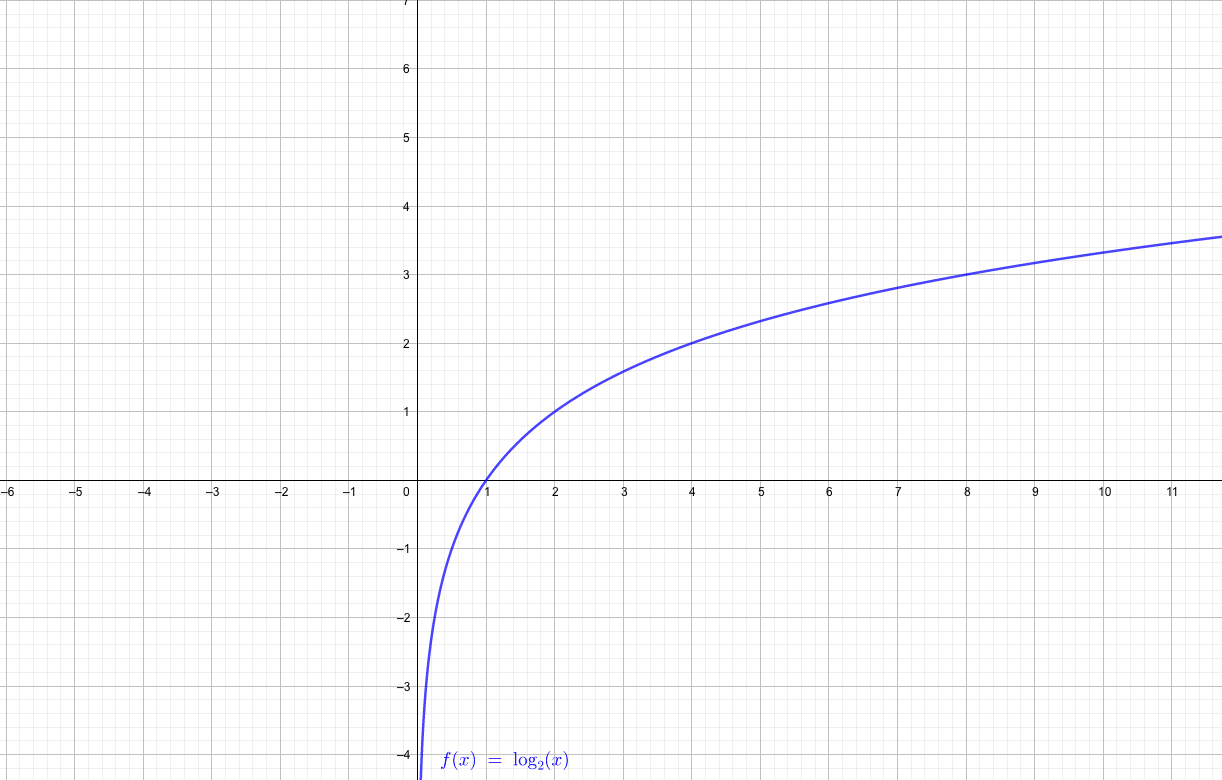

対数関数のグラフ|4つの重要性質
ここでは、対数関数の覚えておきたい4つの性質を押さえましょう。
必ず1を通る
2つの対数関数
- \(y=\log_{\frac{1}{2}} x\)
- \(y=\log_2 x\)
を同時に描いてみると、このようになります。
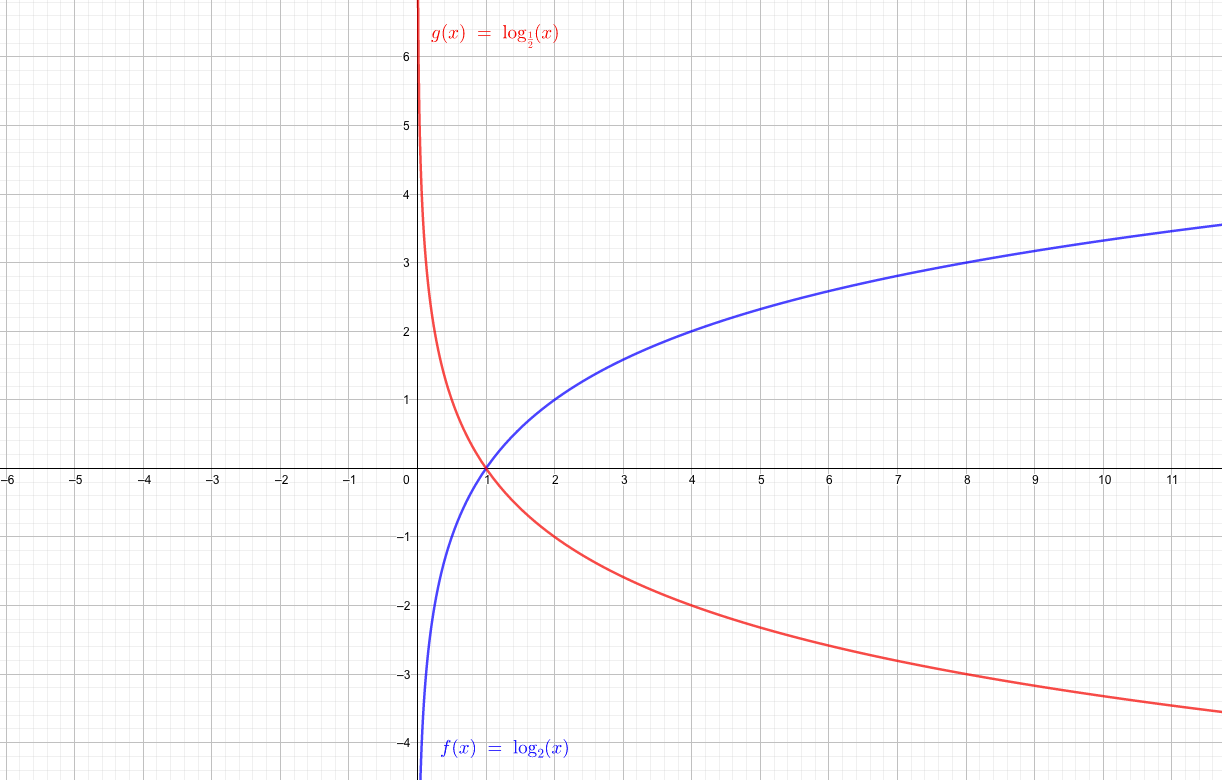

これは対数の定義を思い出してもらえば、当然のことです。
\(y=\log_a x \iff a^y = x\)
を思い出してください。
どんな\(x\)の値でも成り立つように拡張した指数法則では、\(y=0\)のとき、必ず\(x=1\)になる(と定義する)のでしたね。

\(x\)が正のときのみ考え(真数条件)、漸近線(ぜんきんせん)がある
またまた
\(y=\log_a x \iff a^y = x\)
を思い出してください。
底\(a\)の値が正のときのみ、指数関数/対数関数を考えることができ、
正の数\(a\)を何乗しても、正の数にしかならない
という、ムチャクチャ当たり前なことから、\(x>0\)のときしか考えません。
では、\(x\)の値が0に近づくとどうなるのでしょうか。
グラフを見ると簡単で、\(y\)軸に近づきますが、一致することや超えることはありません。



ここで\(a^y = x\)について
- \(a=\frac{1}{2}\)
- \(a=2\)
のときを考えてみましょう。
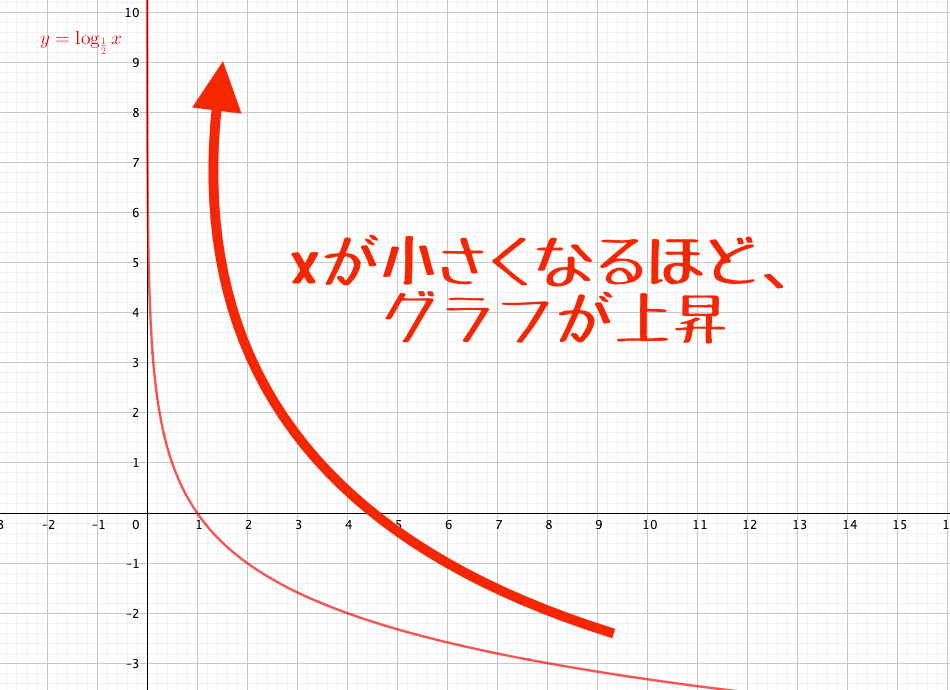
\(a=\frac{1}{2}\)のとき
となることから、\(x\)の値が0に近づく(どんどん小さくなる)とき、\(y\)の値はどんどん大きくなります。

\(a=2\)のとき
\(x\)の値が0に近づいて0.〜と表されるとき、(有理数であれば)分数で\(\frac{1}{ナントカ}\)と表現できます。
この\(\frac{1}{ナントカ}\)を表現するためには、指数\(y\)の値は負となりますね。
そのため、\(x\)の値が0に近づくと、\(y\)の値は次第に小さくなります。
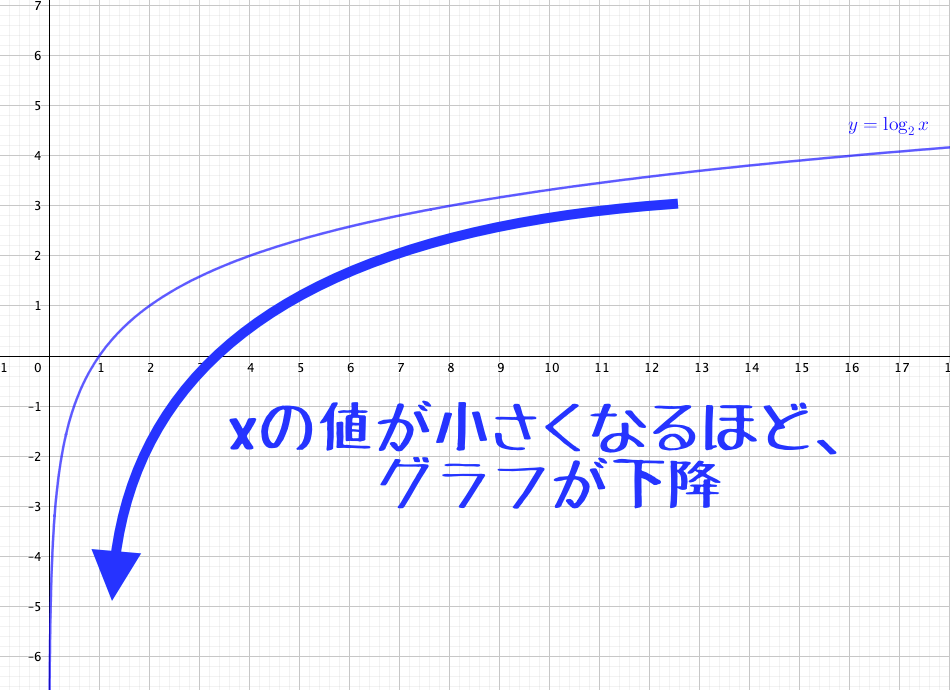
ただどちらの場合も、\(x\)が0になることは決してありません。
小さな数を何乗しても、0になることはないからです。
そのためどちらも\(y\)軸(\(x=0\))に触れることはありません。
ちなみに、この触れてるようだけど、どんなに近づいても決して触れることがない線のことを漸近線(ぜんきんせん)といいます。
指数関数の逆関数
逆関数自体は数Ⅲで登場しますが、指数対数の関係性がよくわかるので知っておくといいでしょう。
参考逆関数とは?グラフから考える『入れ替える』意味とその性質
対数関数\(y=\log _a x\)は
\(y=\log_a x \iff a^y = x\)
であることから、指数関数\(y=a^x\)と見比べてみると、ちょうど\(x\)と\(y\)を入れ替えた関係になっていることがわかります。

実際、2つのグラフを\(a=2\)として描いてみると、\(y=x\)を軸に線対称となっています。
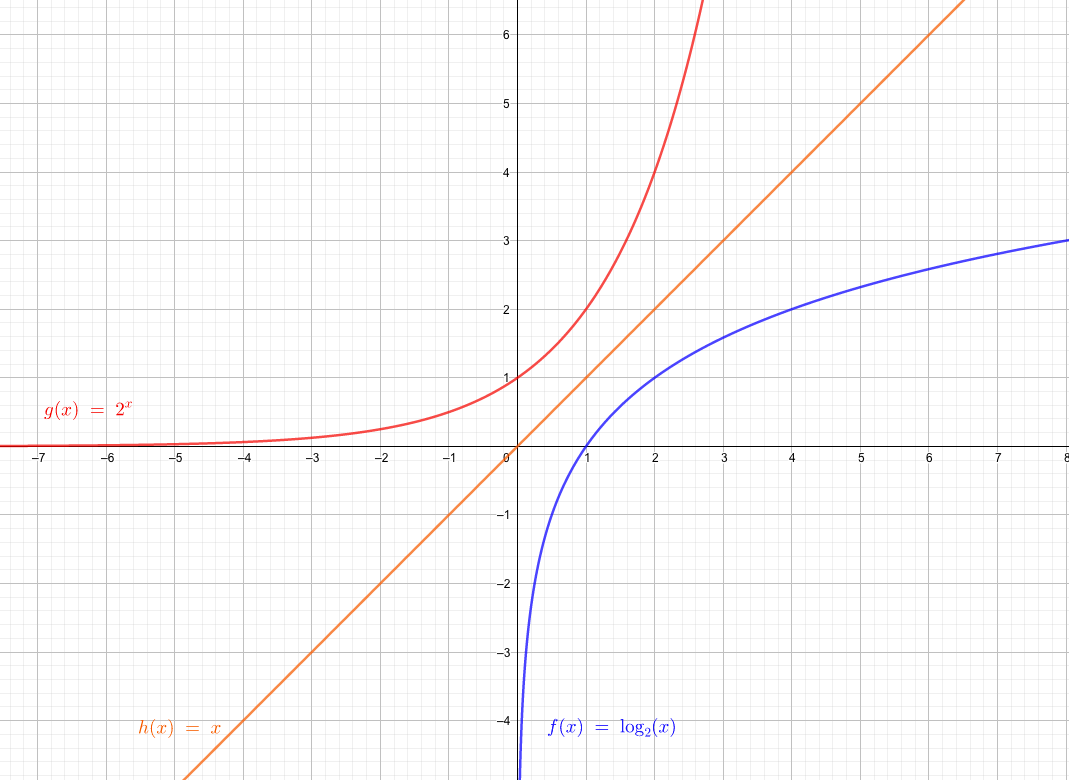

yの増え方がかなり遅い
グラフからもわかる通り、
- \(0<a<1\)(\(a\)の値が0.〜)のとき、\(y\)の値はどんどん小さくなる。
- \(1<a\)(\(a\)の値が1よりも大きい)とき、\(y\)の値はどんどん大きくなる。
という性質があります。
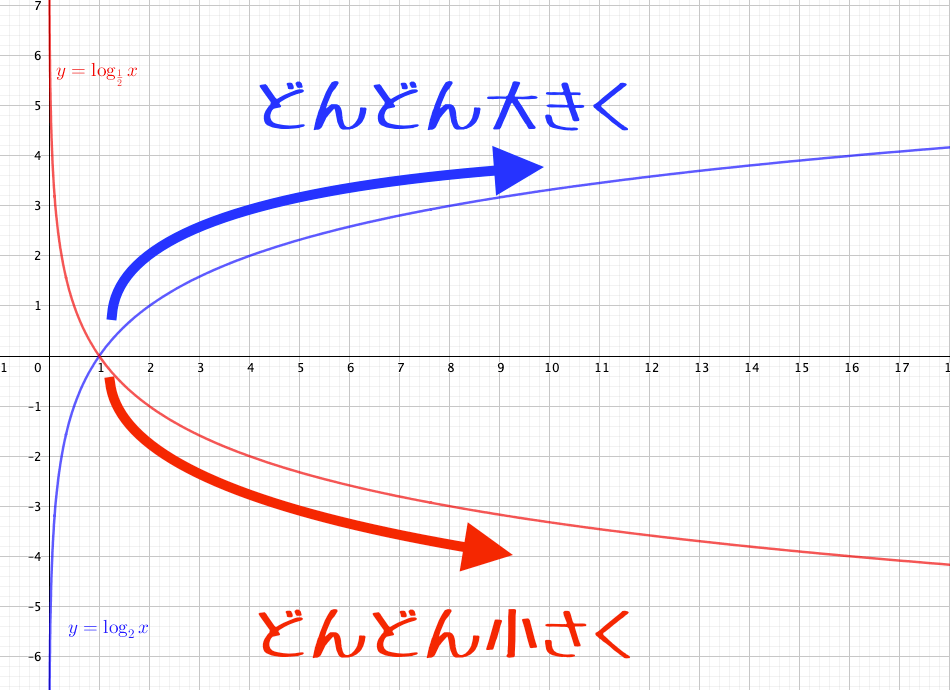
しかし、この\(y\)の値の変化はかなり遅いです。
例えば\(\log _2 x\)において、計算機を使うと
\(x=1000\)のとき、\(\log _2 1000=9.96\cdots\)
\(x=10000\)のとき、\(\log _2 10000=13.28\cdots\)
のように、\(x\)が10倍されていっても、4程度しか増えていません。
ポイント
指数関数は\(x\)が1増えると爆発的に値が上昇するのに対して、対数関数はほとんど増えない。
まとめ

まとめ
対数関数\(y=\log_a x\)は、
- 指数関数に直して考えるとわかりやすい。
- 底\(a\)が1以下の小数か、1以上か場合分けして考える。
- 底の値によらず、必ず点\((1,0)\)を通る。
- \(y\)軸を漸近線にもつ。
- 指数関数とは、逆関数の関係にある。
- \(x\)が増えても、\(y\)の値がほとんど増えない。
対数関数基本的に指数関数との比較や、上記6つの性質がわかっていればそれほど難しくありません。
だからこそ、出題者は複雑な形に見える問題を作るわけですが、対数の演算とグラフを思い浮かべることができれば、全然乗り切れます。

以上、「対数関数について」でした。








