Today's Topic
\(x\)軸となす角が\(\theta\)の直線の傾きを\(\tan\theta\)と表す。



こんなあなたへ
「タンジェントって何?」
「タンジェントの言っている意味がわからない。。。」
この記事を読むと、この意味がわかる!
- \(\tan30^{\circ}\)の値を求めよ。
- 身長168cmのジョナサンの影が56cmの時、南中高度はいくらか。

三角関数を一気に理解したい方への記事は、こちらにまとめてあります。
Contents
タンジェント基本講座|タンジェントの意味を理解しよう
中学校で、こんなグラフを見た記憶はありませんか?
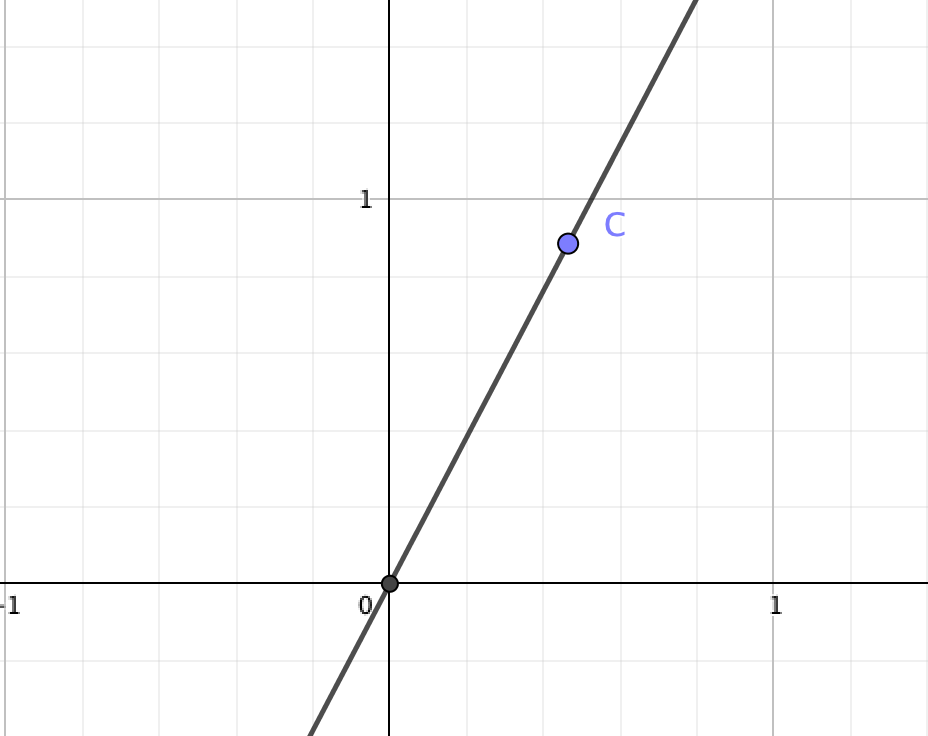









では、この直線\(OC\)と\(x\)軸とのなす角が\(\theta\)だとしましょう。
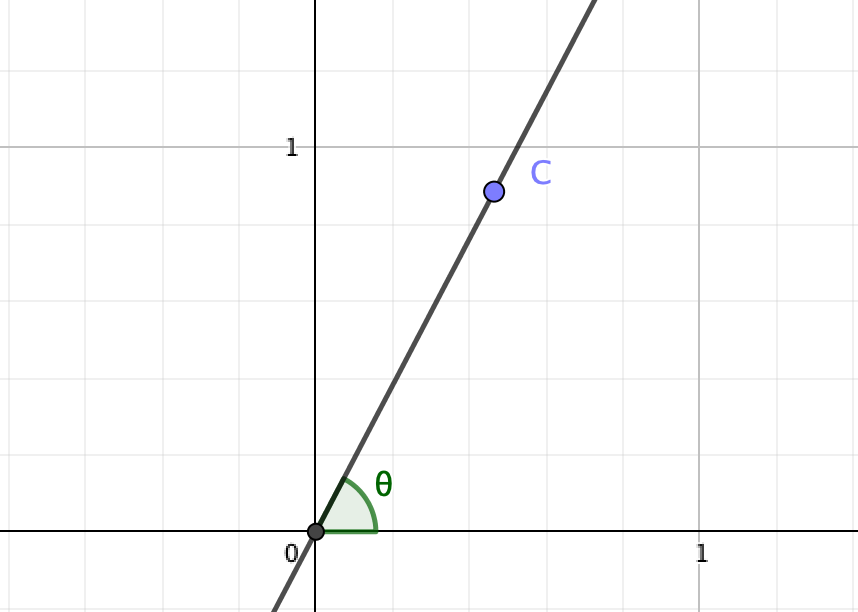

このように、『直線OCと\(x\)軸とのなす角が\(\theta\)』と考えたとき、直線OCの傾き\(a\)は\(\tan\theta\)と表されます。
タンジェントの定義
\(x\)軸となす角が\(\theta\)の直線の傾きを\(\tan\theta\)と表す。




傾きは、このように求められます。
ポイント
$$傾き=\frac{yの増加量\ \ \ \ \ \ }{xの増加量\ \ \ \ \ \ }$$
では原点を基準に、\(x\)の増加量、\(y\)の増加量を考えてみましょう。
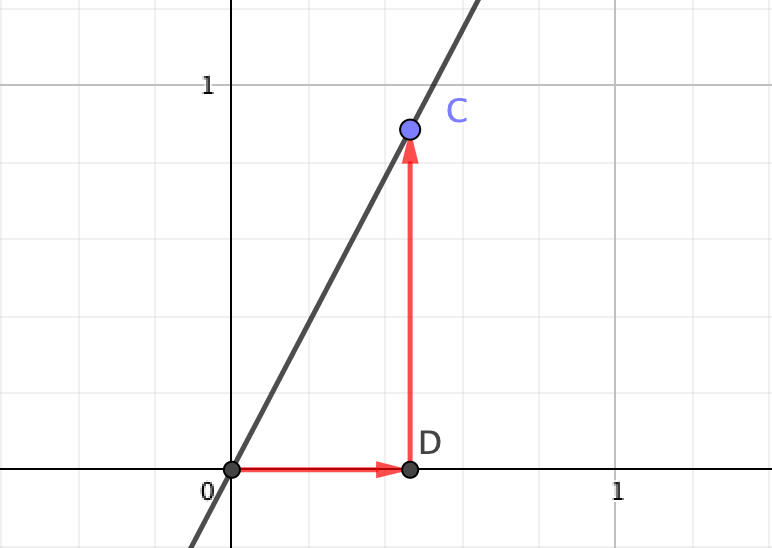



この図にちょっと落書きをしてみると、このようになります。何か見覚えはありませんか?
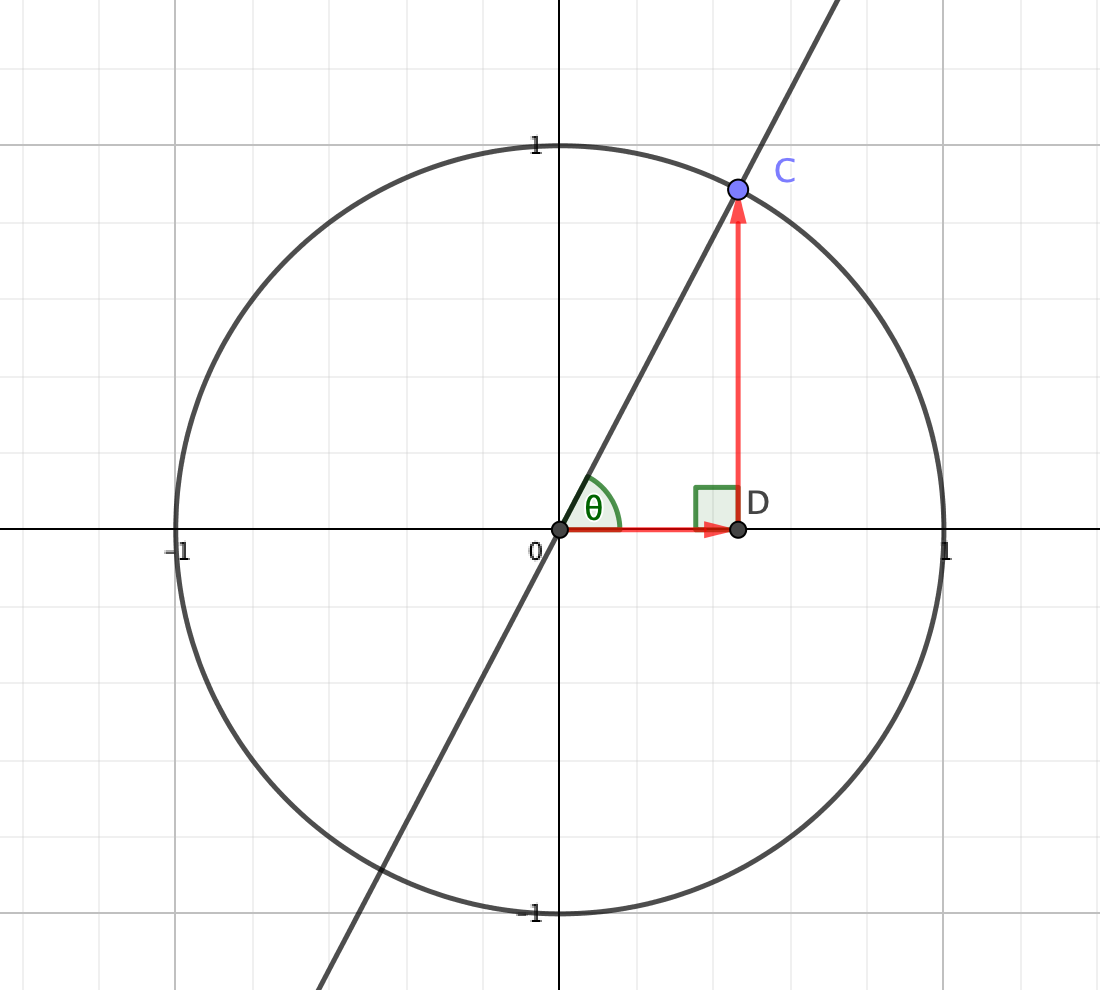





サインコサインについて復習したい人はこちらを参考にしてください。
続きを見る



【中学生でもわかった】サインコサインとは?公式を暗記しなくても、感覚でわかる!
\(\angle DOC=\theta\)とおいたとき、\(OD=\sin\theta,DC=\cos\theta\)と表せます。
傾きを\(\tan\theta\)と表すのですから、
ポイント
$$\tan\theta=\frac{\sin\theta}{\cos\theta}$$
と考えられます。


タンジェント基本講座|【暗記は必要ない】タンジェントの値
の方程式ができたので、ただのあだ名だったタンジェントにも値を定めることができるようになりました。
つまり、タンジェントの値はサインとコサインの値があってのものなんですね。
サインとコサインの講座の時に紹介した、簡単な値表をご覧ください。
| \(\theta\) | \(0^{\circ}\) | \(30^{\circ}\) | \(45^{\circ}\) | \(60^{\circ}\) | \(90^{\circ}\) | \(120^{\circ}\) | \(135^{\circ}\) | \(150^{\circ}\) | \(180^{\circ}\) |
| \(\sin\theta\) | \(\frac{\sqrt{0}}{2}\) | \(\frac{\sqrt{1}}{2}\) | \(\frac{\sqrt{2}}{2}\) | \(\frac{\sqrt{3}}{2}\) | \(\frac{\sqrt{4}}{2}\) | \(\frac{\sqrt{3}}{2}\) | \(\frac{\sqrt{2}}{2}\) | \(\frac{\sqrt{1}}{2}\) | \(\frac{\sqrt{0}}{2}\) |
| \(\cos\theta\) | \(\frac{\sqrt{4}}{2}\) | \(\frac{\sqrt{3}}{2}\) | \(\frac{\sqrt{2}}{2}\) | \(\frac{\sqrt{1}}{2}\) | \(\frac{\sqrt{0}}{2}\) | \(\frac{\sqrt{1}}{2}\) | \(\frac{\sqrt{2}}{2}\) | \(\frac{\sqrt{3}}{2}\) | \(\frac{\sqrt{4}}{2}\) |


このとき、どの値の分母も等しく2で統一されています。
同じ分母を持つ分数同士の割り算は、\(\frac{分子}{分子}\)となります。
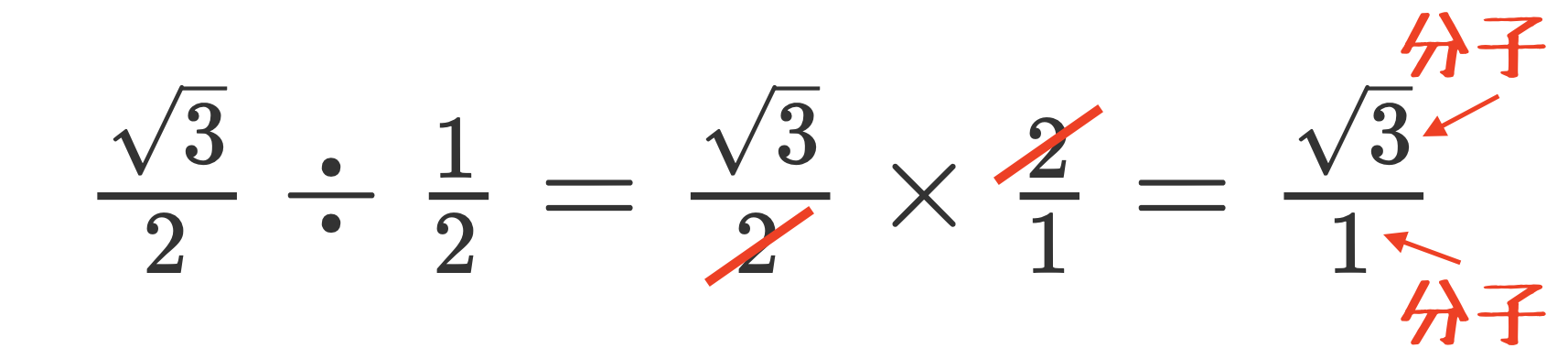
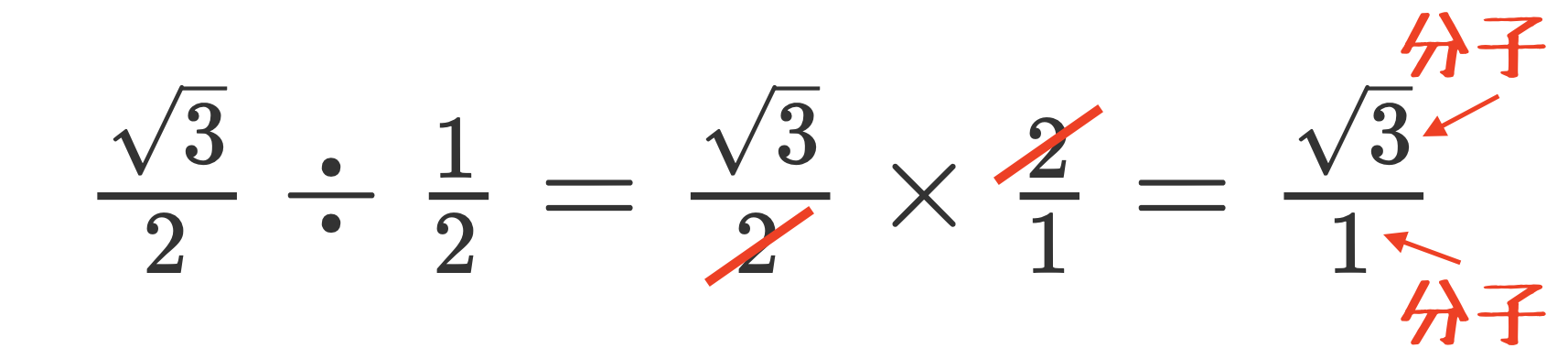
つまりこの表の下に、分子\(\div\)分子をした値を書いてあげればサインコサインタンジェントが一気にわかります。
| \(\theta\) | \(0^{\circ}\) | \(30^{\circ}\) | \(45^{\circ}\) | \(60^{\circ}\) | \(90^{\circ}\) | \(120^{\circ}\) | \(135^{\circ}\) | \(150^{\circ}\) | \(180^{\circ}\) |
| \(\sin\theta\) | \(\frac{\sqrt{0}}{2}\) | \(\frac{\sqrt{1}}{2}\) | \(\frac{\sqrt{2}}{2}\) | \(\frac{\sqrt{3}}{2}\) | \(\frac{\sqrt{4}}{2}\) | \(\frac{\sqrt{3}}{2}\) | \(\frac{\sqrt{2}}{2}\) | \(\frac{\sqrt{1}}{2}\) | \(\frac{\sqrt{0}}{2}\) |
| \(\cos\theta\) | \(\frac{\sqrt{4}}{2}\) | \(\frac{\sqrt{3}}{2}\) | \(\frac{\sqrt{2}}{2}\) | \(\frac{\sqrt{1}}{2}\) | \(\frac{\sqrt{0}}{2}\) | \(\frac{\sqrt{1}}{2}\) | \(\frac{\sqrt{2}}{2}\) | \(\frac{\sqrt{3}}{2}\) | \(\frac{\sqrt{4}}{2}\) |
| \(\tan\theta\) | \(\frac{\sqrt{0}}{\sqrt{4}}\) | \(\frac{\sqrt{1}}{\sqrt{3}}\) | \(\frac{\sqrt{2}}{\sqrt{2}}\) | \(\frac{\sqrt{3}}{\sqrt{1}}\) | \(\frac{\sqrt{4}}{\sqrt{0}}\) | \(\frac{\sqrt{3}}{\sqrt{1}}\) | \(\frac{\sqrt{2}}{\sqrt{2}}\) | \(\frac{\sqrt{1}}{\sqrt{3}}\) | \(\frac{\sqrt{0}}{\sqrt{4}}\) |
ただし、\(\frac{\sqrt{4}}{\sqrt{0}}\)は0で割っているため数として定義できません。


これに注意すると、以下の表ができます。
| \(\theta\) | \(0^{\circ}\) | \(30^{\circ}\) | \(45^{\circ}\) | \(60^{\circ}\) | \(90^{\circ}\) | \(120^{\circ}\) | \(135^{\circ}\) | \(150^{\circ}\) | \(180^{\circ}\) |
| \(\sin\theta\) | 0 | \(\frac{1}{2}\) | \(\frac{1}{\sqrt{2}}\) | \(\frac{\sqrt{3}}{2}\) | 1 | \(\frac{\sqrt{3}}{2}\) | \(\frac{1}{\sqrt{2}}\) | \(\frac{1}{2}\) | 0 |
| \(\cos\theta\) | 1 | \(\frac{\sqrt{3}}{2}\) | \(\frac{1}{\sqrt{2}}\) | \(\frac{1}{2}\) | 0 | \(\frac{1}{2}\) | \(\frac{1}{\sqrt{2}}\) | \(\frac{\sqrt{3}}{2}\) | 1 |
| \(\tan\theta\) | 0 | \(\frac{\sqrt{1}}{\sqrt{3}}\) | 1 | \(\sqrt{3}\) | × | \(\sqrt{3}\) | 1 | \(\frac{\sqrt{1}}{\sqrt{3}}\) | 0 |
このようにタンジェントは自分で出すことが超簡単。
覚えるよりも、導出する方法を身につけることをオススメします。
タンジェント基本講座|タンジェントの公式
サインコサインの関係式にこのようなものがありました。
ポイント
\(\sin^2\theta+\cos^2\theta=1\)
この式の両辺を\(\cos^2\theta\)で割ってみると、
左辺の\(\frac{\sin^2\theta}{\cos^2\theta}\)は、次のように変形できる。
よって
ポイント
$$\tan^2\theta+1=\frac{1}{\cos^2\theta}$$




タンジェント基本講座|【いつ使う?】タンジェントの活用例


タンジェントは値の求め方が非常に簡単で、暗記の必要なんてまるでありません。
ですがタンジェントの考えかた自体には非常に重要な要素が含まれています。
ここでは実際に、タンジェントがどれだけ有用か見ていきましょう。
日常場面からタンジェントを学ぶ:傾きから角度を求める
タンジェントは角度と(直線の)傾きをつなぐ重要なものです。
例として、坂道の傾斜角度を求めてみましょう。
皆さんはこんな標識見たことありませんか?


これは100m進んだ時、9mだけ高さの変わる坂道だということを表しています。
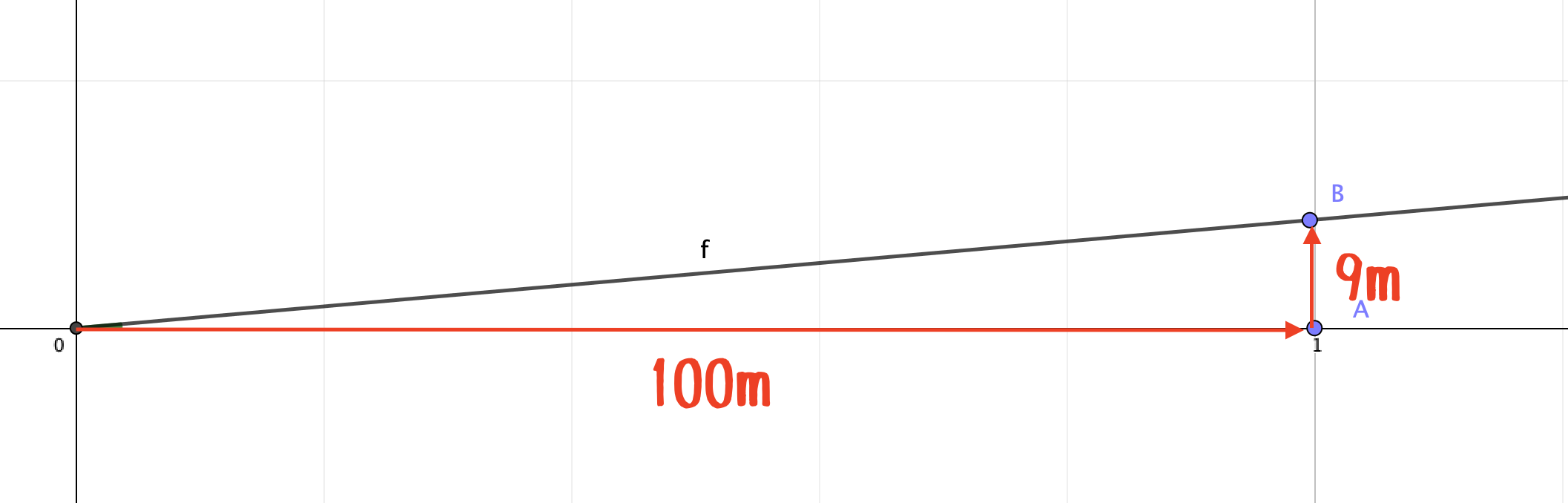



傾きは\(\frac{9}{100}=0.09\)となりますから、傾斜角度\(\angle AOB =\theta\)とおくと、\(\tan\theta=0.09\)と表せます。
この\(\theta\)の値を調べるには、実際に計算機で近い値を探す方が手っ取り早でしょう。すると、
と大体近い値が手に入りました。


つまり例のような坂は、傾斜角度は約5度ということがわかります。
日常場面からタンジェントを学ぶ:影の長さ
皆さんは自分の影で遊んだことがありますか?
影はよく観察すると面白いもので、太陽の位置によって長さが異なります。


身長170cmの男子Aが次のような実験をしました。
- 夏:約33cm
- 冬:約272cm
となった。
影の頭部とAくんの頭部を結んだ直線の傾きを求めてみると、
夏:\(\frac{170}{33}=5.151\cdots\)
冬:\(\frac{170}{272}=0.625\)
となっており、この直線上に太陽があるはずです。
\(\tan\theta=5.151\cdots\)となるような\(\theta\)を探してみると
と比較的近い値がわかりました。
これにより、ある地点の夏の一番高い日の高度(南中高度)は約78.8度とわかりました。
同じように冬の場合も考えてみます。
\(\tan\theta = 0.625\)となるような\(\theta\)を探してみると
と比較的近い値がわかりました。
これにより、ある地点の冬の一番高い日の高度(南中高度)は約32度とわかりました。
このような実験から、夏場の方が冬場よりも南中高度は高い位置にあるということがわかります。


タンジェント基本講座|まとめ


まとめ
- タンジェントは、\(x\)軸と傾き\(\theta\)で交わる直線の傾きを表している。
- \(\tan\theta\)の値を求めるためには、傾きを表していることに着目し、\(\frac{\sin\theta}{\cos\theta}\)を計算すれば良い。
- \(\tan^2\theta+1=\frac{1}{\cos^2\theta}\)を使えば、\(\cos\theta\)の値だけで\(\tan\theta\)の値が分かる。
- タンジェントは角度と長さ、傾きをつなぐ超重要キーワードである。
苦手意識を持っていた人でも、図的な意味さえわかればそれほど難しくないことが理解できたのではないでしょうか。
暗記する部分はかなり少なく、値も公式も自分で導出した方が絶対ラクです!


サインコサインと合わせて理解しておくようにしましょう!
以上、「タンジェントの基本講座」でした。
Q.\(\tan30^{\circ}\)の値を求めよ。
以下のような図を頭の中、もしくはノートやテストの端に描けたら迷うことはないでしょう。
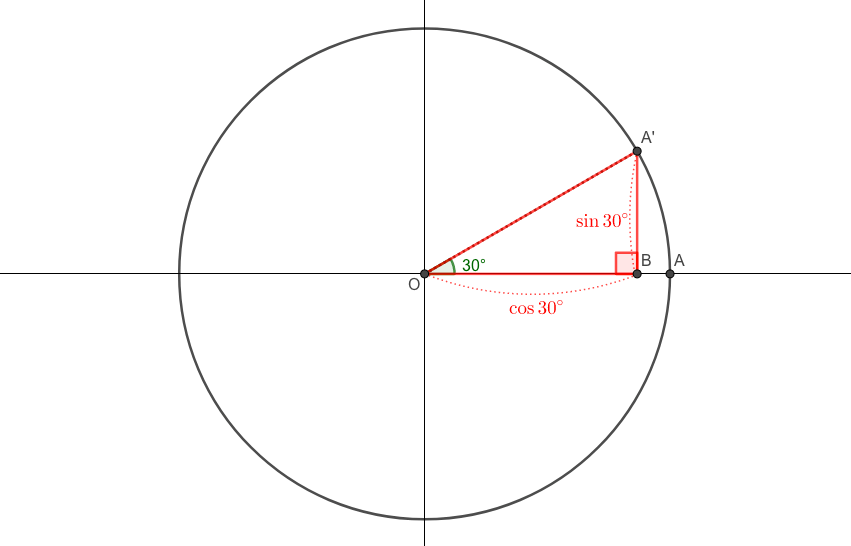

直線\(OA'\)の傾きを求めればいいだけですから、
$$\frac{\sin30^{\circ}}{\cos30^{\circ}}=\frac{1}{\sqrt{3}}$$
Q.身長168cmのジョナサンの影が56cmの時、南中高度はいくらか。
ジョナサンの影の長さをコサインの値、身長をサインの値とみなすと、タンジェントの値は
$$\tan \theta =\frac{168}{56}=3$$
これを満たすような\(\theta\)の値を電卓等で探すと、
$$\tan 71^{\circ}= 2.904\cdots$$
が結構近い。つまり南中高度は約71度。









