Today's Topic
$$y - f(a) = -\frac{1}{f’(a)}(x-a) $$


この記事を読むと、この意味がわかる!
- 法線の方程式の求め方
- 法線と接線の関係とその証明
法線の定義
まず、あなたは法線の定義を説明することができますか?
案外疎かにされがちなので、もう一度確認しておきます。
定義
つまり法線には
- 接線と垂直
- 接点を通る
という2つの条件が必要になるわけです。
法線の方程式の求め方
法線の方程式は、次の公式で求めることができます。
ポイント
関数\(f(a)\)の点\(\left(a,f(a)\right)\)における法線の方程式は、
$$y - f(a) = -\frac{1}{f’(a)}(x-a) $$
で求められる。
接線の方程式\(y - f(a) = f’(a)(x-a)\)と見比べると、傾きが\(-1\)倍した逆数の関係になっていることがわかります。
例題
三次関数\(y = x^3 -2x +1 \)の点\((2,5)\)における法線の方程式を求めよ。
\(y’ = 3x^2 -2 \)より、接点における接線の傾きは\(3\cdot 2^2 -2 = 10\)
よって、法線の傾きは\(-\frac{1}{10}\)
傾き\(-10\)の直線が接点\((2,5)\)を通るように平行移動すれば良いので
$$y - 5 = -\frac{1}{10} (x-2)$$
整理して、
$$y = -\frac{1}{10}x + \frac{26}{5}$$
法線の方程式の証明
図のような直線\(y= mx\)と、それに原点で直交する直線 \(y=nx\) を考える。
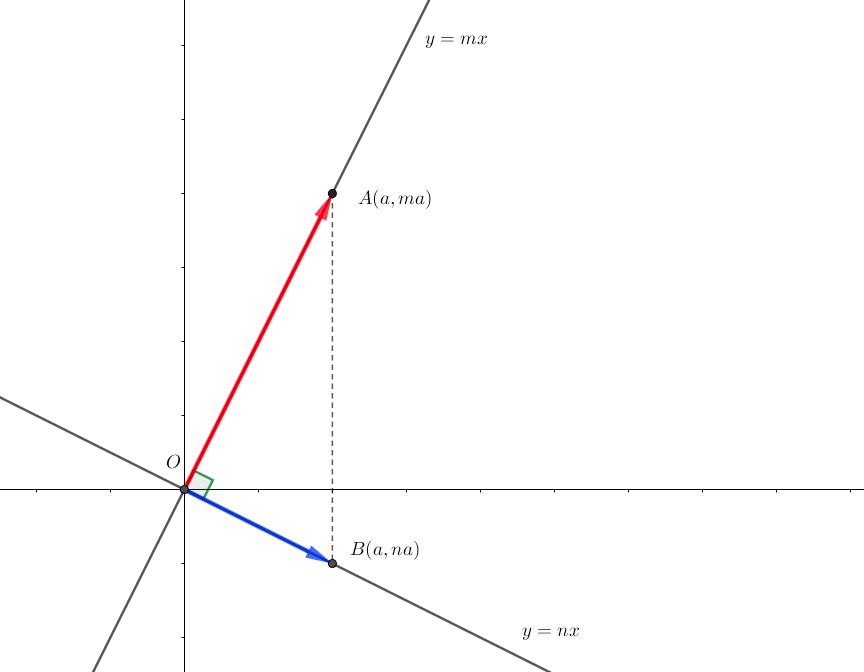
ベクトルの内積を用いると、
図より、
ここで条件より\(a\neq\)なので\(1+mn = 0\)
よって \(n = -\frac{1}{m}\) となるので、直線\(y= mx\)と直交する直線の傾きは\(-\frac{1}{m}\)と表せる。
(証明おわり)
法線って結局、接線と垂直に交わっているというだけなので、証明はこれでOK。
なお「直線\(y= mx\)と直交する直線の傾きは\(-\frac{1}{m}\)と表せる」証明は、他にも何種類か方法があります。
しかしここであえてベクトルを用いたのは、直角という条件とベクトルの内積の相性の良さを知ってもらいたいから。
実は接線の方程式もベクトルを用いたほうが簡単に求まる場合があるので、ぜひ習得しておきたいスキルです。
法線の方程式っていつ使うの?
結論、高校数学ではそれほど重要視されるような場面はないのかなと思います。
応用例はいくらでも作れるため小問として出てくることが多いですが、大学数学では3次元空間における図形や外積と呼ばれるものに応用したりします。

まとめ

まとめ
直線\(y=mx\)と垂直に交わる直線の傾きは\(-\frac{1}{m}\)
法線の方程式を求めるためには、
- 接線の傾きをもとに、直交する直線の傾きを求めて
- 接点を通るように平行移動すればOK
内容自体は難しくないので、接線問題のついで出てくるだろう的な感じで覚えておきましょう。
以上、「法線の方程式について」でした。








