Today's Topic
増減表を描くためには、
- 導関数を求め、微分係数の正負が切り替わる\(x\)の値を探し、
- 右肩上がりか、右肩下がりなのかを書き加え、
- 値を埋めていけば良い。



この記事を読むと、この意味がわかる!
- 増減表を描く最速の方法
- 増減表の弱点
増減表とは
増減表は、曲線のグラフを描く際に使われる、グラフの変化を簡略的に表した表のことです。
曲線のグラフを描く際に重要なことは、
- どの地点でカーブするのか
- どのようにカーブするのか
の2点。
増減表は、微分係数(接線の傾き)を用いて『どの地点でカーブするのか』は評価することができます。


増減表とグラフ
まず例として、次の2次関数を考えてみましょう。
例題
$$y=-x^2+3$$
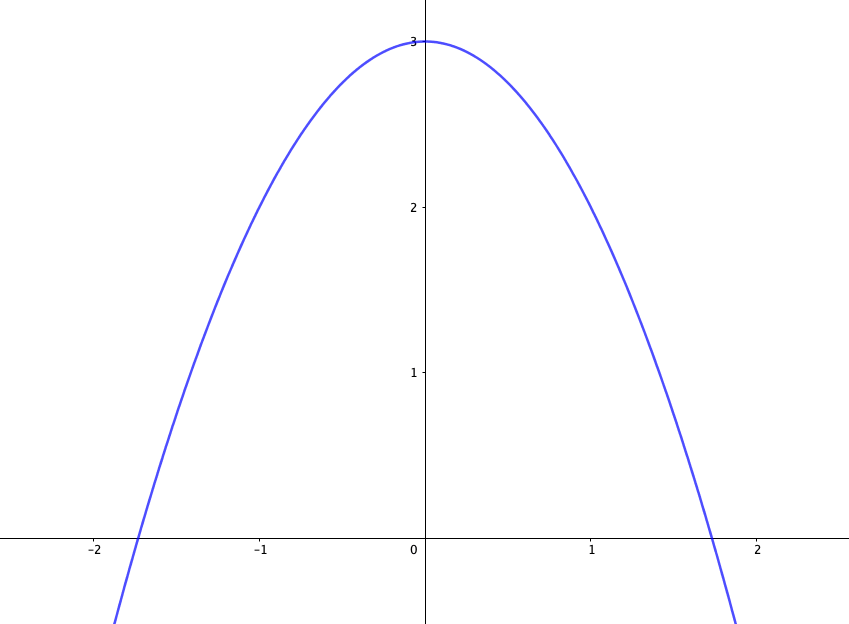
この二次関数の増減表は下記のようになります。
| $$x$$ | $$\cdots$$ | $$0$$ | $$\cdots$$ |
| $$y'$$ | $$+$$ | $$0$$ | $$-$$ |
| $$y$$ | $$\nearrow$$ | $$3$$ | $$\searrow$$ |
増減表とグラフを見比べてみると、あることに気がつきます。
それは・・・。
微分係数\(f’(a)\)の符号が切り替わる点でU字カーブしている
ということ。


では、なぜこの地点でカーブするのでしょうか。
\(y'\)は微分係数、つまりその点における接線の傾きを意味していました。
つまり、\(y'=0\)とは、傾き0(\(x\)軸と平行)の直線になっているということを表します。
また、増減表の\(y'\)の行を見ると
- \(x<0\)の間の\(y'\)は正→\(x<0\)の間は接線の傾きが+
- \(x>0\)の間の\(y'\)は負→\(x>0\)の間は接線の傾きがー
ということもわかります。
つまり増減表を見るだけで、グラフは\(x\)の値が大きくなると、接線が
昇る→平らになる→降る
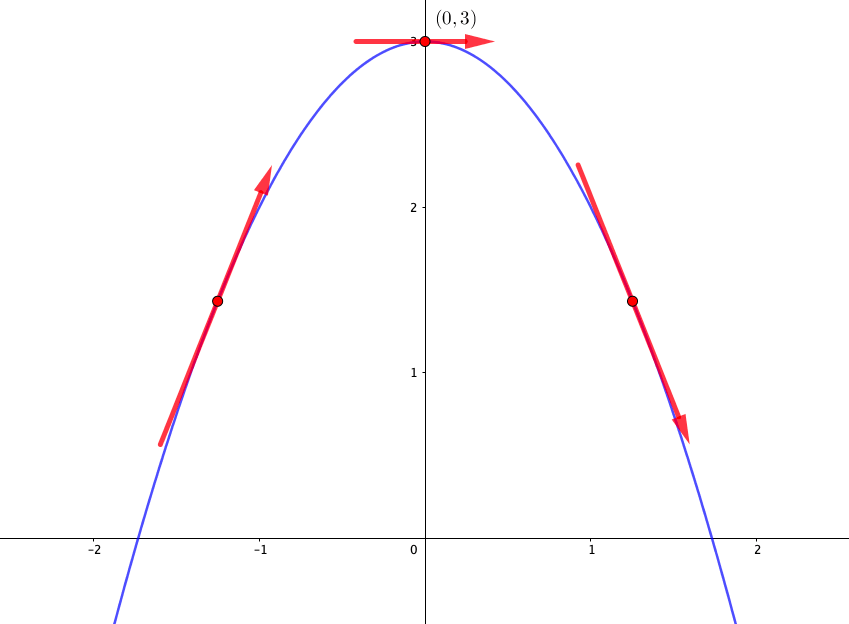
という動きをしていることがわかります。
これにより、増減表だけで、\(y=x^2+3\)は(微分係数の正負が入れ替わる)\(x=0\)を境にカーブしていることがわかるのです。

ちなみにカーブの境となっている\(x=0\)のような点のことを、極値といいます。
極値は曲線のグラフであれば必ず存在するわけではなく、しっかりとチェックする必要があります。
それについては、こちらの記事でご紹介します。
-

-
【極大値・極小値】定義と求め方→最大値・最小値とは求め方が異なる!
続きを見る
増減表の書き方
次のステップで増減表を書くと、最短でグラフの概形を求めることができます。
次の例題をもとに増減表を描いてみましょう。
例題
$$y=3x^3-x+1$$
STEP1:導関数\(f’(x)\)を求め、\(f’(x)=0\)を満たす\(x\)の値を調べる
これにより、極値がわかります。
\(y' = 9x^2-1\)なので、\(y'=0\)となるのは\(x=\pm \frac{1}{3}\)のときです。
STEP2:増減表に定義域と\(f’(x)=0\)を満たす\(x\)の値をかき、間に\(\cdots\)を挟む
この段階までで、次のような増減表が描けます。
| $$x$$ | $$\cdots$$ | $$-\frac{1}{3}$$ | $$\cdots$$ | $$\frac{1}{3}$$ | $$\cdots$$ |
| $$y'$$ | $$0$$ | $$0$$ | |||
| $$y$$ |


STEP3:\(\cdots\)のときの微分係数の正負を調べて\(f’(x)\)の行に書き、\(y\)の行に「右肩上がり」・「右肩下がり」を矢印で描く。
この手順で、どこでグラフがカーブしているのかがおおよそわかります。
| $$x$$ | $$\cdots$$ | $$-\frac{1}{3}$$ | $$\cdots$$ | $$\frac{1}{3}$$ | $$\cdots$$ |
| $$y'$$ | $$+$$ | $$0$$ | $$-$$ | $$0$$ | $$+$$ |
| $$y$$ | $$\nearrow$$ | $$\searrow$$ | $$\nearrow$$ |


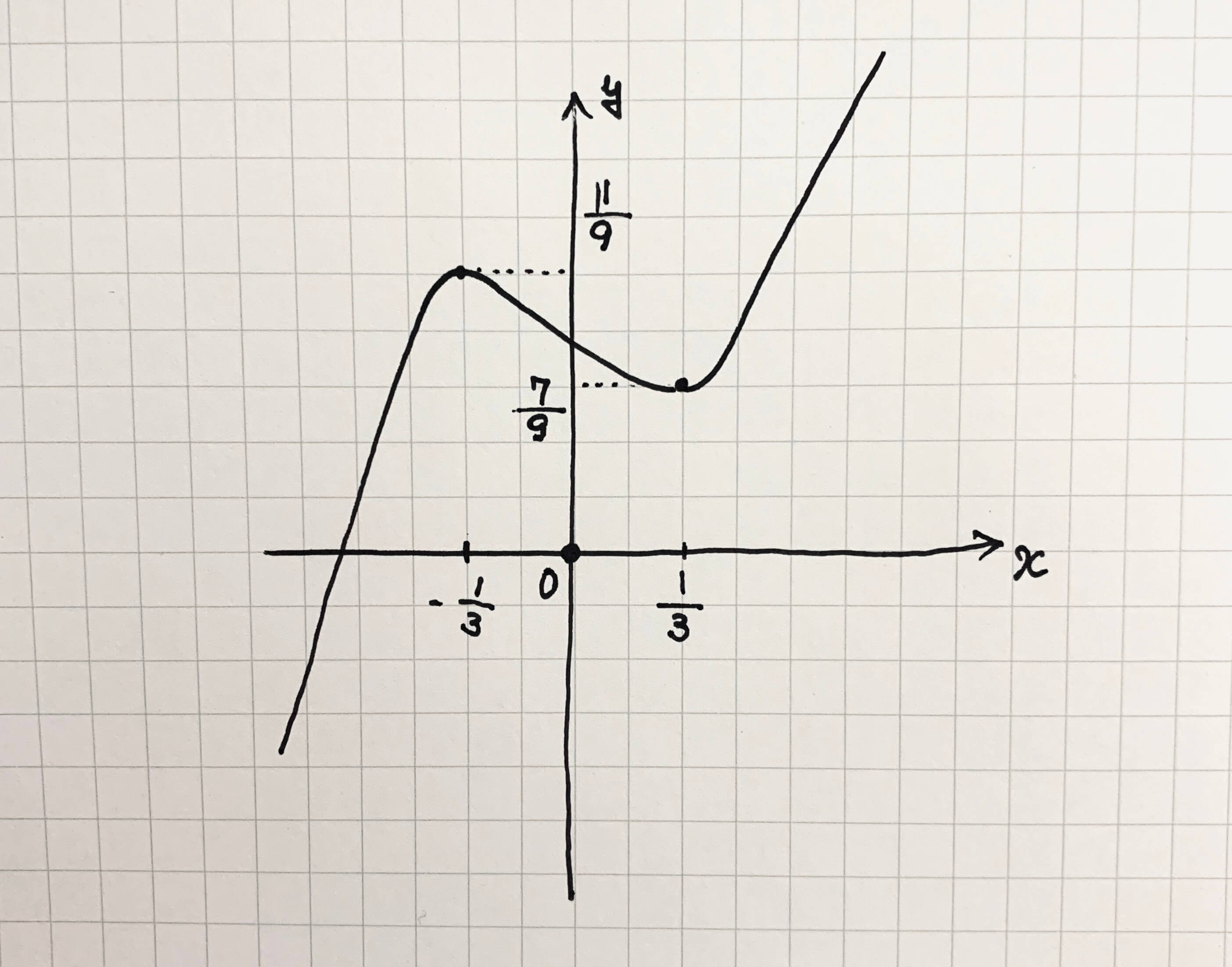
STEP4:値が求められるなら、穴埋めする
残りの空白の部分を計算して埋めていきます。
| $$x$$ | $$\cdots$$ | $$-\frac{1}{3}$$ | $$\cdots$$ | $$\frac{1}{3}$$ | $$\cdots$$ |
| $$y'$$ | $$+$$ | $$0$$ | $$-$$ | $$0$$ | $$+$$ |
| $$y$$ | $$\nearrow$$ | $$\frac{11}{9}$$ | $$\searrow$$ | $$\frac{7}{9}$$ | $$\nearrow$$ |


完成!
完成図(小春作)





【実際のグラフ】
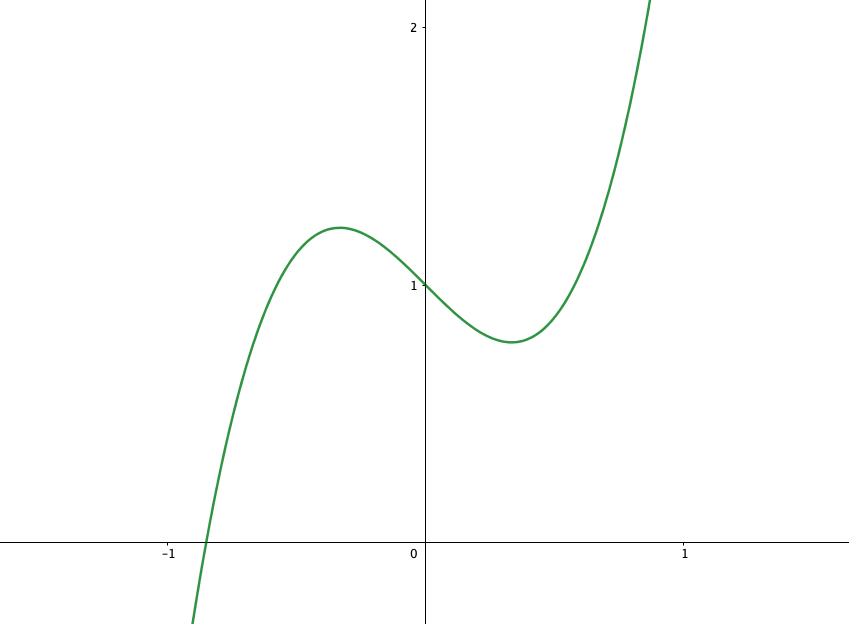
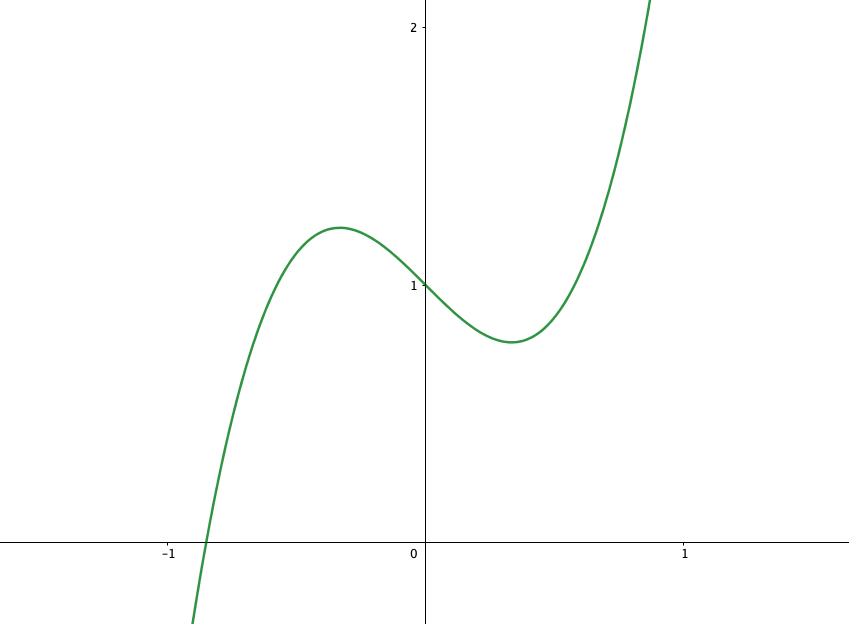
増減表の注意点
さて、このように便利な増減表ですが、あまり教えられることのない弱点がいくつか存在します。




次の例題を参考に解説しますね。
例題
\(-2≦x≦2\)における\(y=x^3-1\)のグラフを描け。
(増減表)
| $$x$$ | $$\frac{1}{2}$$ | $$\cdots$$ | $$0$$ | $$\cdots$$ | $$-\frac{1}{2}$$ |
| $$y'$$ | $$×$$ | $$+$$ | $$0$$ | $$+$$ | $$×$$ |
| $$y$$ | $$-\frac{9}{8}$$ | $$\nearrow$$ | $$-1$$ | $$\nearrow$$ | $$-\frac{7}{8}$$ |
(グラフ)
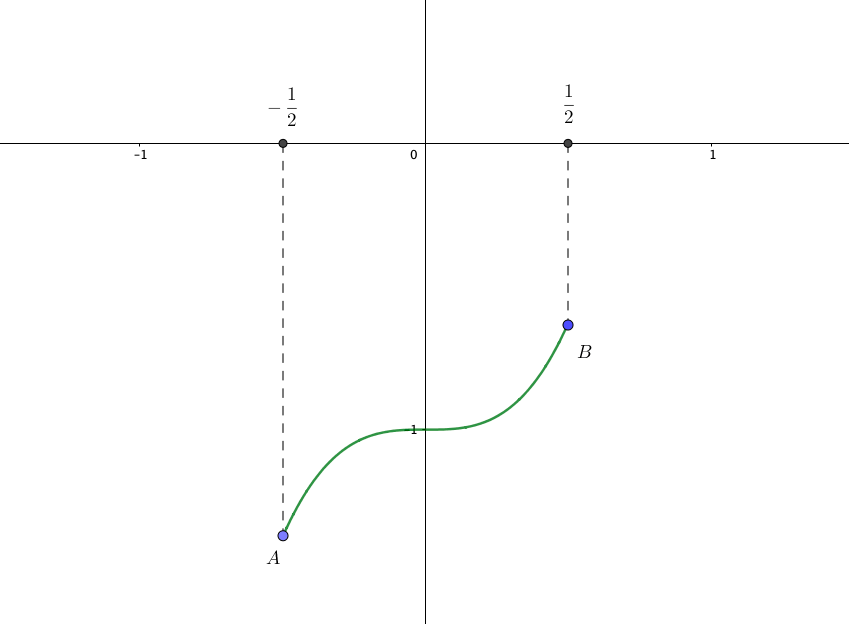

注意1:端点では微分不可
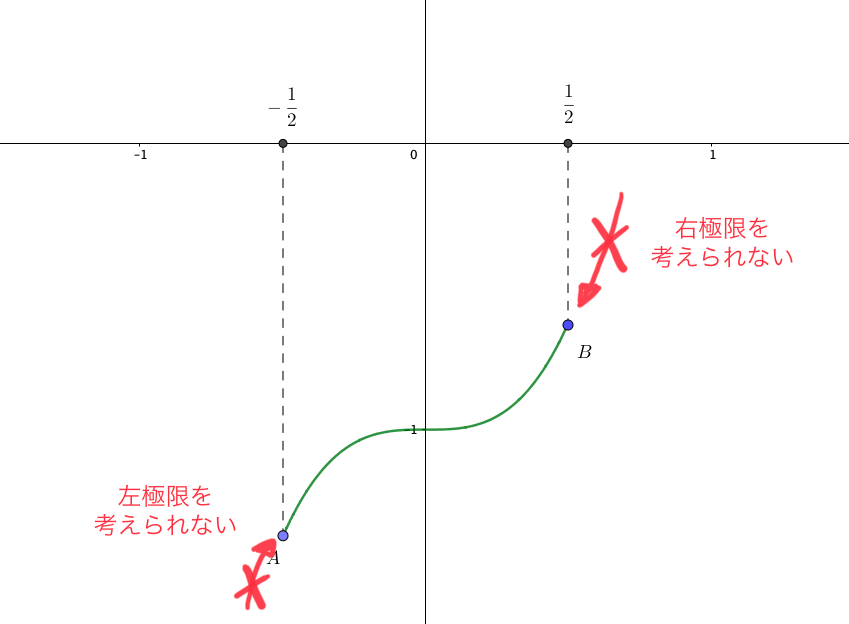
増減表の\(x=\pm\frac{1}{2}\)のとき、\(y'\)の行にバツがついていますね。
このバツは書かなくてOKなのですが、なぜバツなのかはしっかり理解する必要があります。
ここで重要なのは微分(導関数)の定義。
詳しくは微分可能の定義で扱いますが、この極限の値が存在するのは、右極限と左極限の値が一致するときだけ。
しかし、端点ではそれより前、もしくは先の点の存在を考えることができません。
つまり
- \(x=-\frac{1}{2}\)では右極限を考えることができない
- \(x=\frac{1}{2}\)では左極限を考えることができない
ため、微分可能ではないのです。

注意2:曲がり方がわからない
下のように、離れた2点を想像してください。
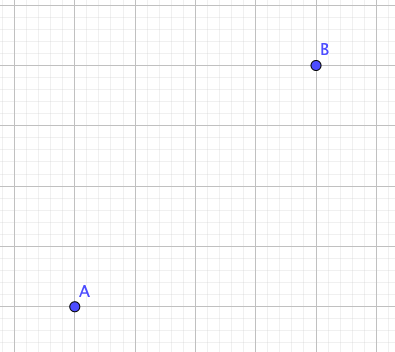

点Aと点Bを結ぶとき、結び方には次の3種類があります。
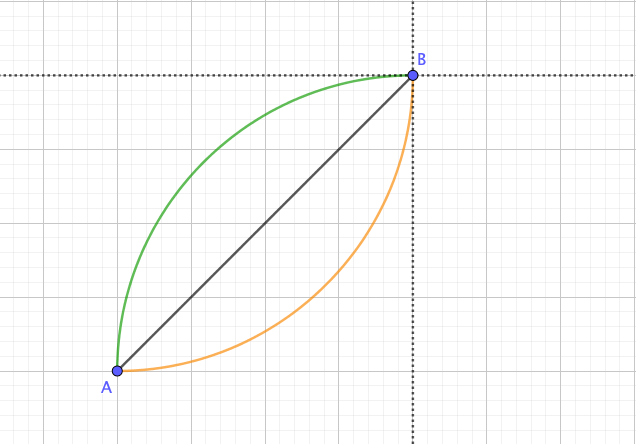

曲線の例で言えば、図の緑色とオレンジの曲がり方がありますね。
しかしながら増減表では、このどちらの曲がり方をするかはわかりません。




曲がり方まで考慮した、より正確なグラフを描くためには、カーブの仕方まで正確に知る必要があり、それは数Ⅲの2階微分を利用した変曲点の話になります。
しかし方程式にはある程度グラフの形が決まっており、「三次関数だからこのカーブの仕方をするだろう」という憶測でグラフを描くことになります。


まとめ


まとめ
増減表は、接線の傾きに着目してグラフの概形を把握しようとしている。
微分係数の正負が切り替わる点で、グラフはカーブする。
増減表を描くためには、
- 導関数を求め、微分係数の正負が切り替わる\(x\)の値を探し、
- 右肩上がりか、右肩下がりなのかを書き加え、
- 値を埋めていけば良い。
今回は増減表について扱いましたが、弱点があるという認識が重要。
数Ⅱで扱うグラフは三次関数や、四次関数程度なので、グラフの概形を覚えておけば問題ありません。
しかし数Ⅲや大学数学で登場するような、複雑な方程式などは一体どんな形をするのか見当もつきません。
数Ⅲでは増減表の弱点を、「変曲点」と呼ばれるもので補います。


以上、「増減表の描き方と弱点」についてでした。









