Today's Topic
平均変化率
$$\frac{f(b)-f(a)}{b-a}$$

小春
楓くん、平均変化率って結局何なの?
傾き

楓

小春
えっ・・・。
傾き

楓
この記事を読むと、この意味がわかる!
- 平均変化率の定義
- 平均変化率を使う場面
平均変化率とは
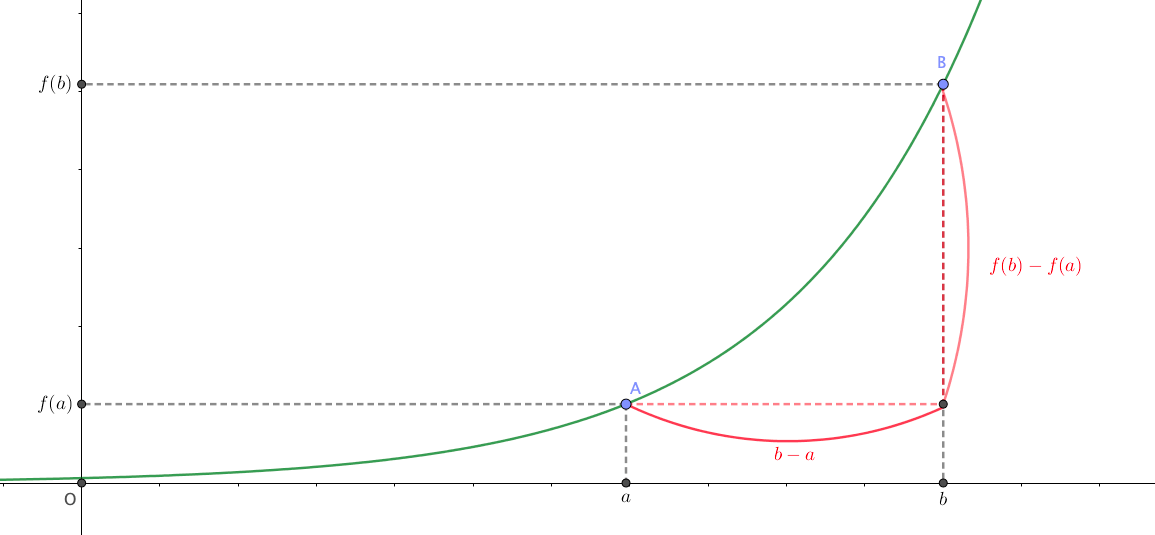
図のような、適当なグラフ上に2点A,Bを考えます。
このとき、平均変化率は
$$\frac{f(b)-f(a)}{b-a}$$
で求めることができます。

楓
分母は\(x\)座標の差分、分子は\(y\)座標の差分になっているね。
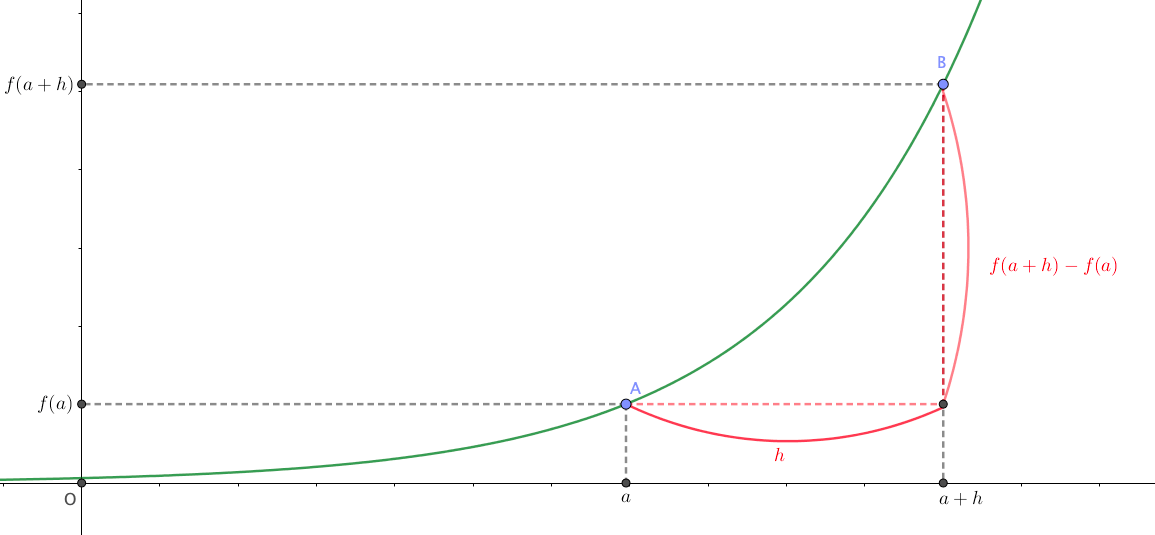
またこの図のように、差分に着目して座標をとった場合、
$$\frac{f(a+h)-f(a)}{h}$$
のように書くこともできます。

小春
言ってる内容は上も下も同じことだね。
つまり平均変化率は、
『\(x\)が■だけ増えたとき、\(y\)は●だけ増える』
ということを表しています。
直線であれば一定ですが、曲線であれば調べる部分によって異なります。
平均変化率、と聞くと不気味ですが、結局これは2点A,Bを結んだ直線の傾きを求めているにすぎません。

楓
難易度的には中学数学ってことね。
言葉の定義は置いといて、平均変化率と聞いたときは傾きと捉えてOKです。
平均変化率を使う場面
平均変化率は、主に微分係数の導出の時に用いられます。
が、平均変化率といわれても「ハイハイ傾きね」と理解してしまえば十分。
具体例
例題
A,Bの平均変化率と、C,Dの平均変化率を求めよ。
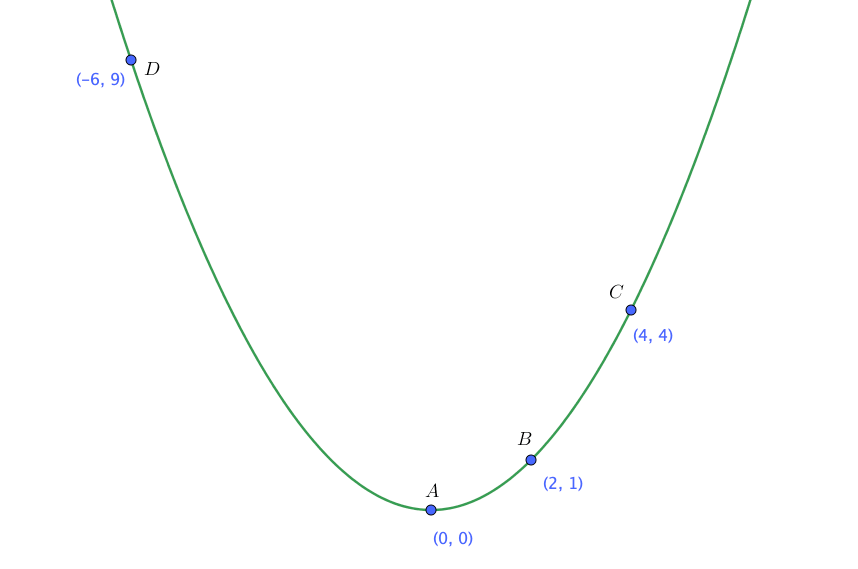
平均変化率は、2つの点を結んだ直線の傾きを求めればOK。
なので、
$$A,Bの平均変化率$$
$$\frac{1-0}{2-0}=\frac{1}{2}$$
$$\frac{1-0}{2-0}=\frac{1}{2}$$
$$C,Dの平均変化率$$
$$\frac{4-9}{4-(-6)}=-\frac{1}{2}$$
$$\frac{4-9}{4-(-6)}=-\frac{1}{2}$$

楓
曲線の平均変化率は、どの2点を結ぶかによって変化することも覚えておこう!
まとめ

小春
ほ、ほんとに傾きのことなんだ・・・
そだよ。経験上、次のようなことが言える!

楓
- 傾き→直線の単元
- 平均変化率→微分の単元

楓
平均変化率は、微分の時にかなり重要な考え方だから、しっかり抑えておこうね。








