Today's Topic
微分係数
$$\lim_{h \to 0}\frac{f(a+h)-f(a)}{h}$$





この記事を読むと、この意味がわかる!
- 微分係数の求め方と、意味
- 微分係数を使う場面
微分係数とは?
微分係数は
で定義された数。
一般にこれを\(f'(a)\)と表します。
これは2点A,Bの距離を、どんどん縮めたときの平均変化率を表しています。


微分係数の意味
まずは2点A,Bの平均変化率
を考えてみましょう。
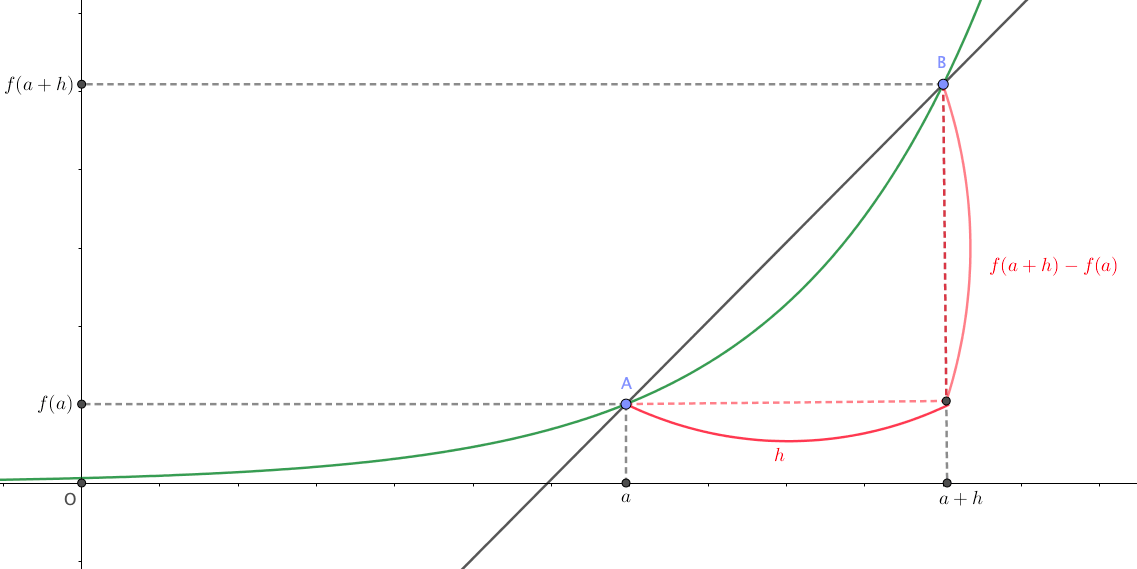
平均変化率は、実際のところ直線ABの傾きを求めているだけでしたね。
この2点A,Bの距離をどんどん0に近づけて(\(h\to0\))みると、直線ABは次のような動きをします。
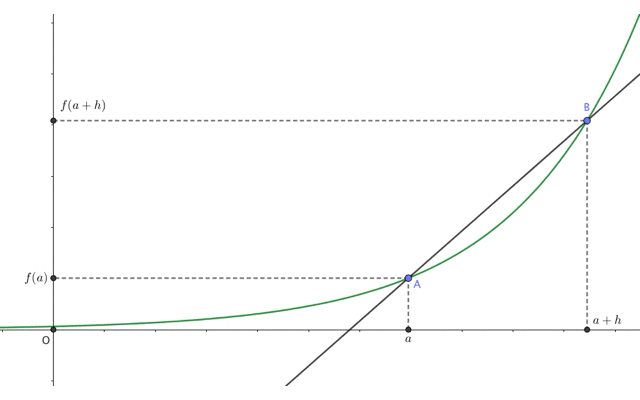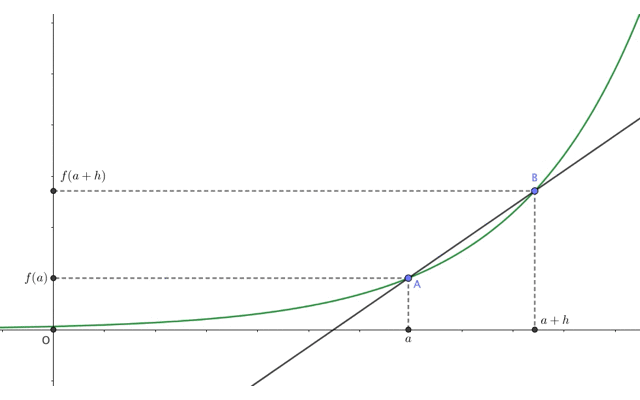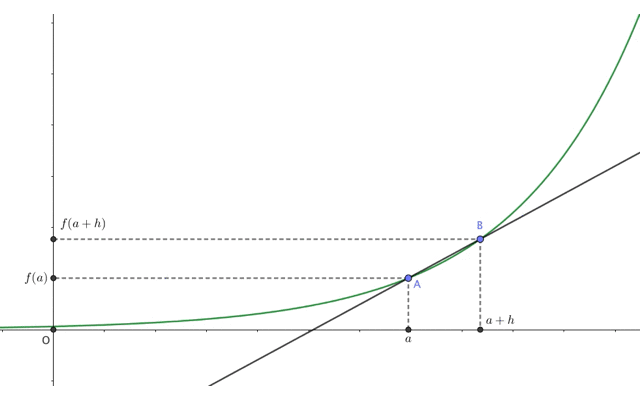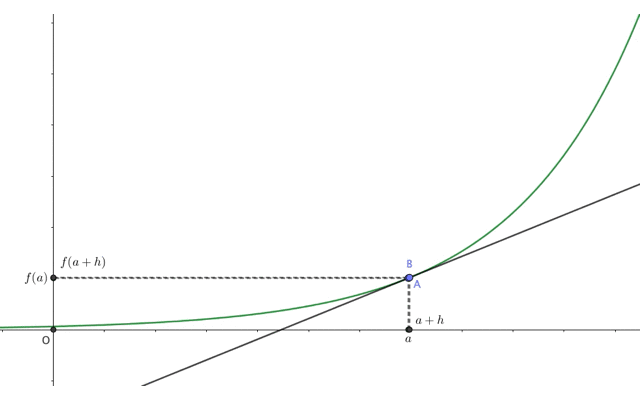
ご覧の通り、最終的に直線ABは点Aにおける\(f(x)\)の接線になりました。
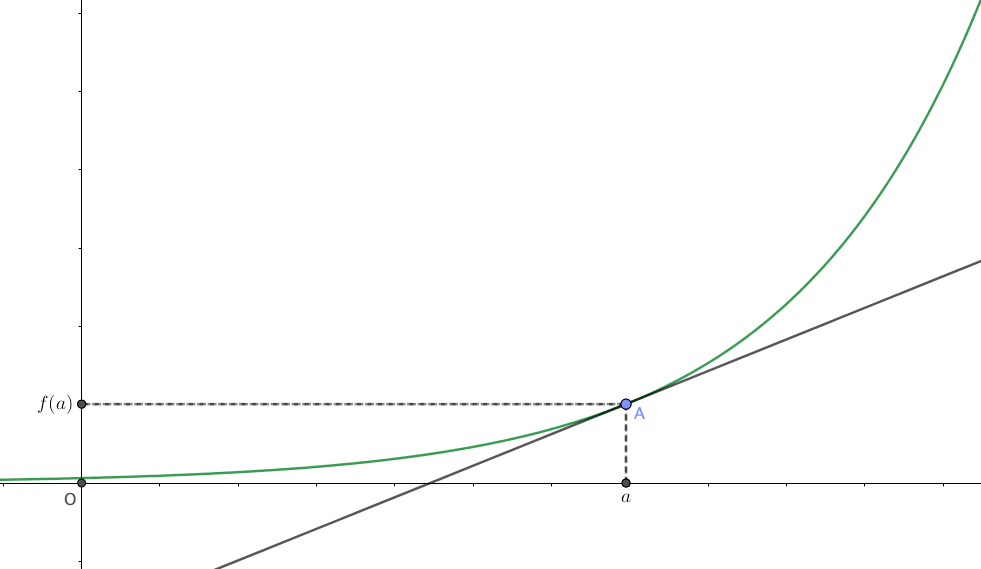
ただしこれはあくまで\(h\to0\)なので、直線ABが点Aにおける接線と完全に一致するわけではありません。

微分係数を使う場面
微分係数を使う目的はただ1つ。
すでに書いたように点Aにおける接線の傾きを求めるためだけです。


数学において、微分はかなり重宝されます。
ただ接線の傾きを求めているだけなのに、なぜそれほど重視されるのでしょうか。
その理由は接線の持つ意味にあります。
微分係数は(少し未来の)増加レベルを表す
ここでは微分からちょっと離れて、接線の傾きの意味について考えてみます。
微分係数導出の練習も兼ねて、次の例題をやってみましょう。
例題
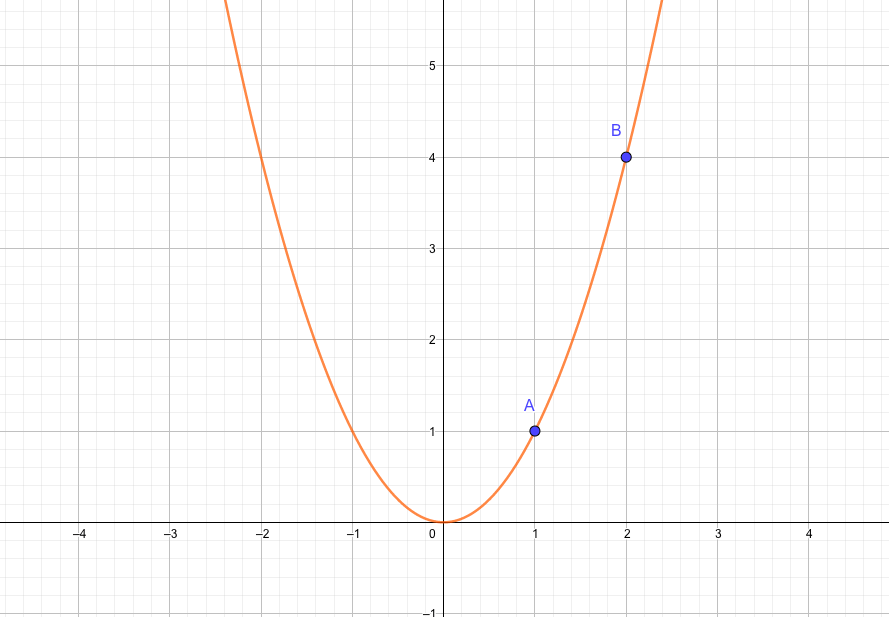
関数\(y=x^2\)上の2点\(A(1,1),B(2,4)\)における接線の傾きを求めてみよう。

\begin{align} f'(2) &= \lim_{h\rightarrow 0}\frac{f(2+h)-f(2)}{h}\\\ &= \lim_{h\rightarrow 0}\frac{(4+4h+h^2)-(2^2)}{h}\\\ &= \lim_{h\rightarrow 0}(4+h)\\\ &= 4\\\ \end{align}
このことから、点Aにおける接線の傾きよりも、点Bにおける接線の傾きの方が大きいということがわかりました。
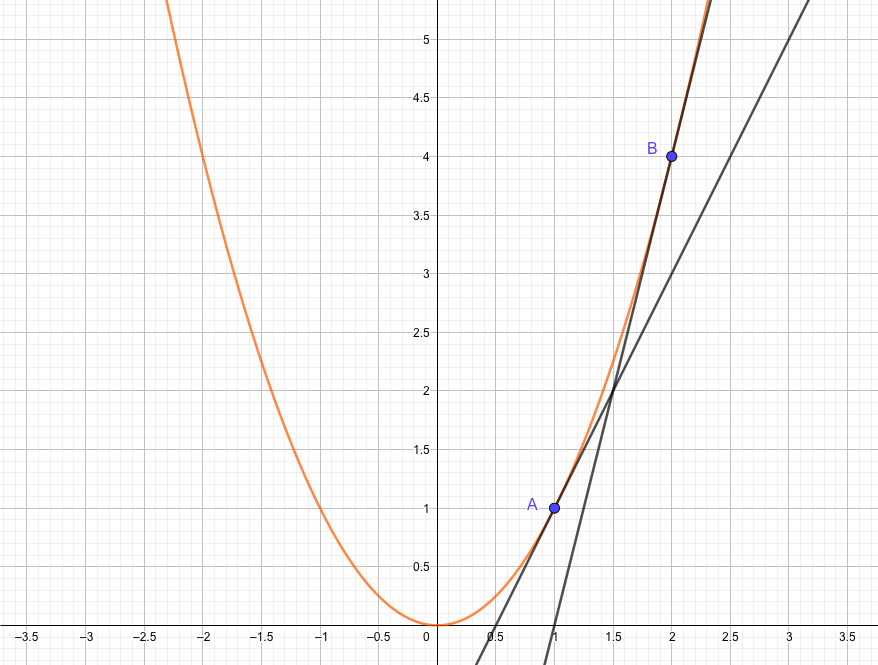
ここでもう一度微分の求め方を見直してみると、点A、点Bのどちらの微分も超短い距離\(h\)だけ離れた点を結んだ直線を考えていました。

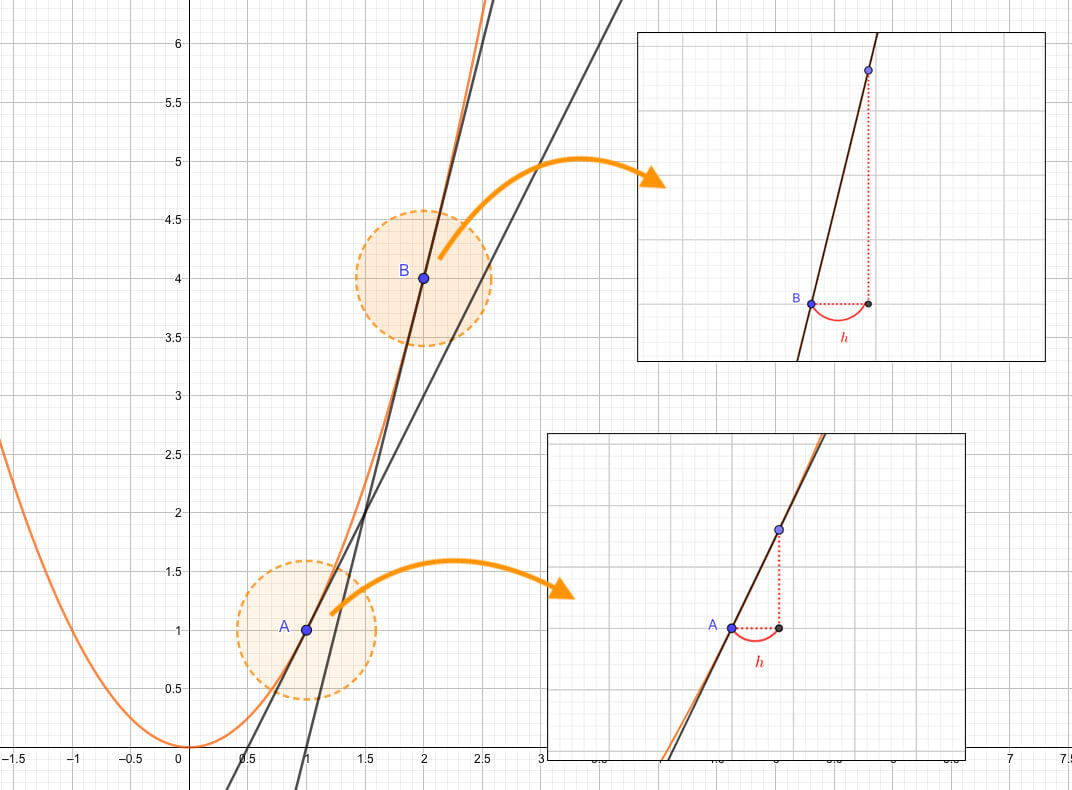

接線の傾きがより大きいということは、ちょっとだけ進んだときの変化の割合がより大きいということ。
すなわち\(x\)の値がちょっと増えただけで、\(y\)の値がより急激に増加するということが言えます。
この考え方を使うと、グラフの形がある程度予測できるようになります。
ある方程式が与えられていて、途中までグラフが描けていたと仮定しましょう。

このグラフの点A以降の形を知りたいとき、点Aにおける微分係数を求めてみます。
その値によって、次のように形を予測することができるというわけです。
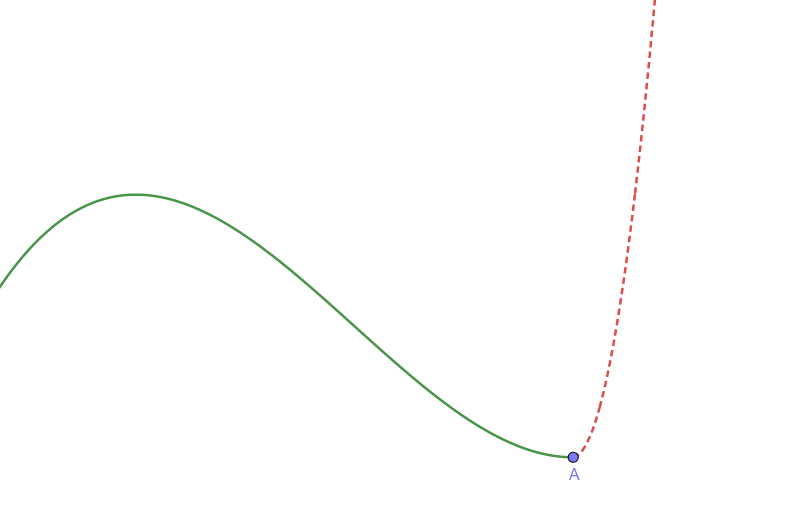
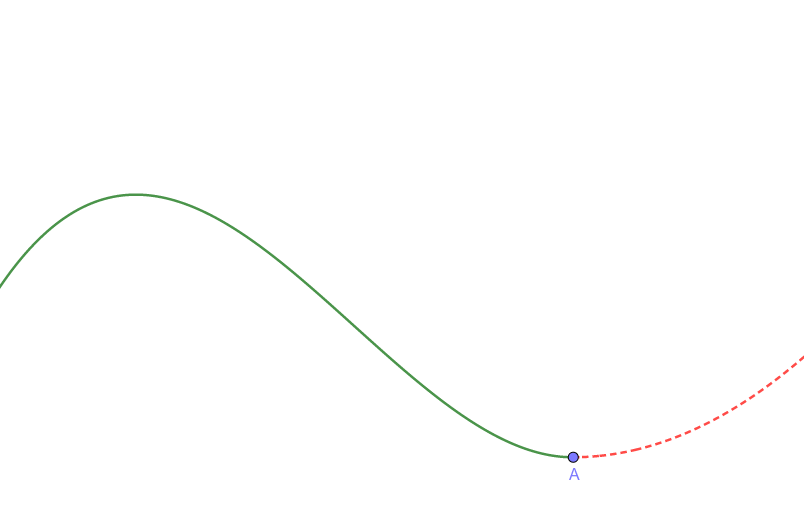
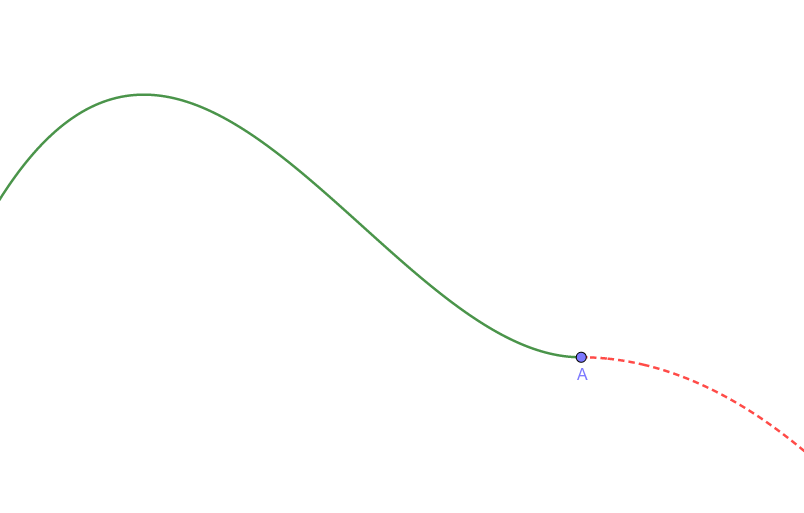
- 点Aでの微分係数が大きい→急激に値が増加

- 点Aでの微分係数が小さい→緩やかに値が増加

- 点Aでの微分係数がマイナス→負の方向に値が増加


導関数との違い
微分係数は、グラフ上のある一点を定めて、その1点における接線の傾きを表していました。
しかし毎回毎回1点ずつ調べるわけにはいかないですね。

そこでグラフ上のどの点でも、\(x\)座標の値さえわかれば、そこの接線の傾きがわかるように生まれたのが導関数です。
つまり導関数は、好きな点の微分係数を求めるための関数と捉えておけばOK。
詳しくは導関数の記事で解説します。
-

-
【導関数】って結局ナニ?微分係数との違いなどを解説。
続きを見る
まとめ


まとめ
- 微分係数とは
$$\lim_{h \to 0}\frac{f(a+h)-f(a)}{h}$$
で求められる値。 - 微分係数は、接線の傾きを表す。
- グラフの形を(大まかに)知るためには、微分係数の大きさを調べれば良い。
ここまで細かく微分係数を解説したのは、数学を追求するほどこの意味合いが強くなるからです。
ぜひ基本を疎かにせず、しっかりと理解しておいてください。


以上、「微分係数ってナニ?」でした。