Today's Topic
$$y-f(a) = f’(a)(x-a)$$




この記事を読むと、この問題がわかる!
- 関数\(y= x^3+2x+2\)の\(x=3\)における接線の方程式を求めよ。
- 三次関数\(y=ax^3\)の接線が直線\(y=x-1\)であるとき、\(a\)の値と接点の座標を求めよ。

Contents
接線の方程式は3STEPでOK
ここでは接線の方程式を確実に求められる手順を紹介します。
接線の問題はいろんなタイプがありますが、基本的にこの3STEPを踏めば、だいたい解けます。
次の例題を通して、具体的に見ていきましょう。
例題
三次関数
$$f(x) = x^3 - 2x^2 +1$$
の点\(A(1,1)\)における接線の方程式を求めよ。
STEP1 導関数\(f’(x)\)の値を求める
接線の傾きという、非常に重要な要素を表す導関数\(f’(x)\)の値を導出します。
これにより、どこでも好きな点における接線の傾きを求められる導関数が手に入りました!
なぜ\(f’(x)\)が接線の傾きを表しているのかは、こちらの記事をご覧ください。
-

-
【導関数】って結局ナニ?微分係数との違いなどを解説。
続きを見る
STEP2 接点を求めて、\(f’(x)\)に代入
曲線は接点の場所によって、接線の傾きが異なります。
そのためどこで接しているかはかなり重要なポイント。
今回は問題で与えられているので、そのまま代入します。
\begin{align} f’(1) &= 1(3-4)\\\ &= -1 \\\ \end{align}
これにより、特定の点における接線の傾きである微分係数がわかりました!
STEP3 傾き\(f’(a)\)の直線を、接点を通るように平行移動
\(x=a\)のとき接線の傾きは、微分係数\(f’(a)\)と表せたので、
は \(x=a\)における接線と平行な直線を表しています。
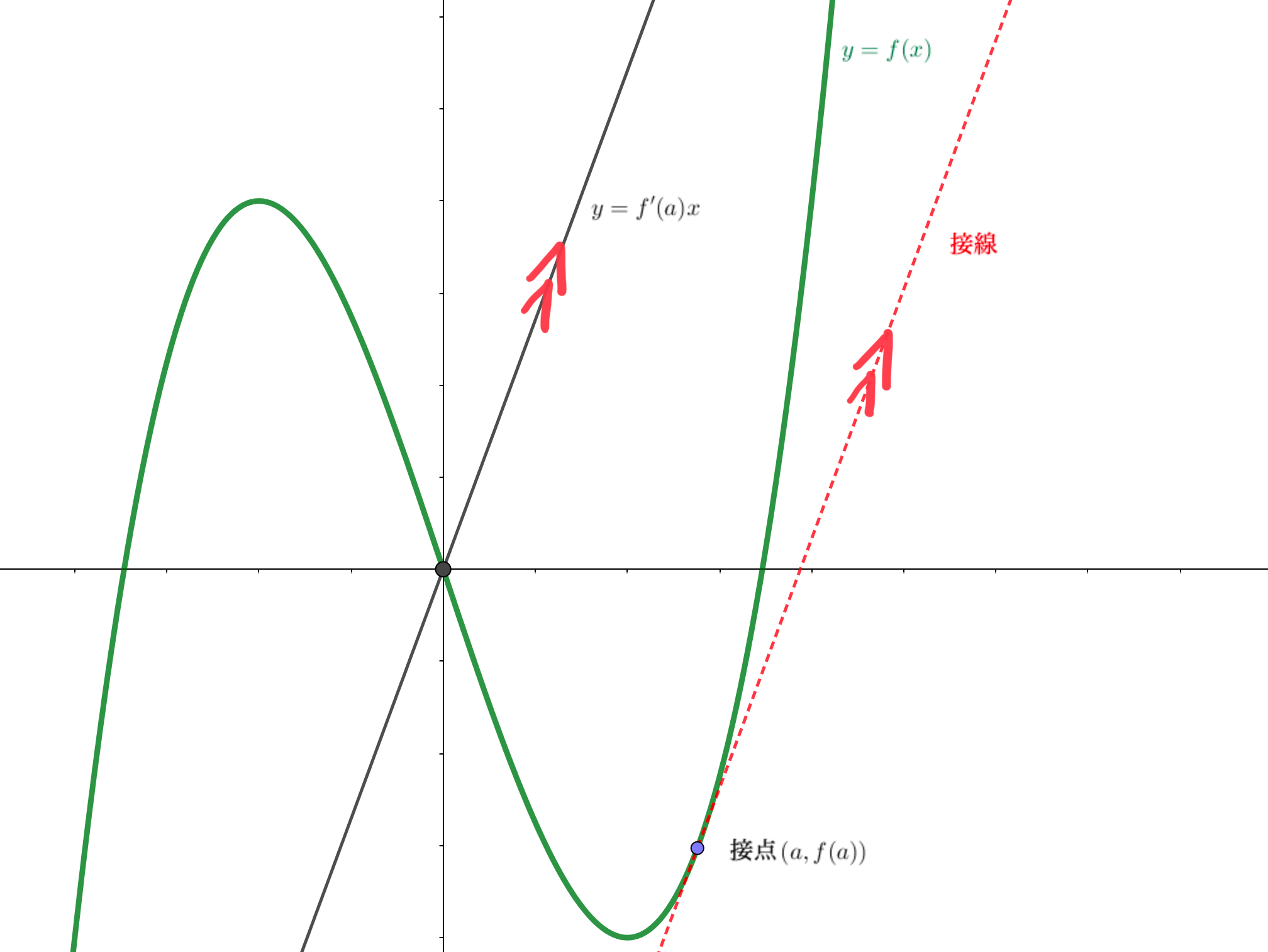

この直線が、接点を通るように平行移動してあげれば、みごと接線の方程式を表現することができます。
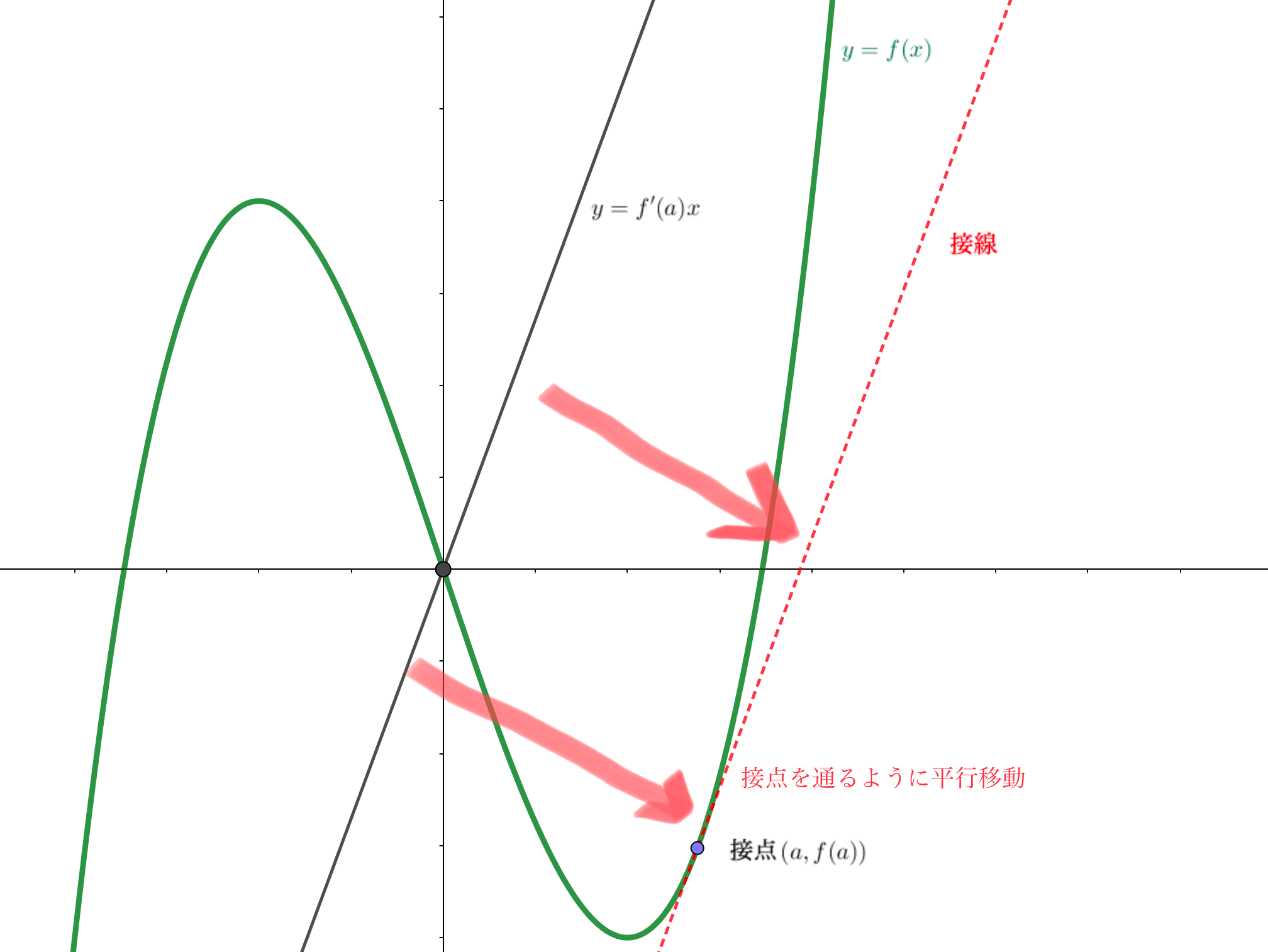

ポイント
接線の方程式
$$y-f(a) = f’(a)(x-a)$$
よって 接線の方程式は、$$y-1 = -(x-1)$$
平行移動について復習したい人はこちらを参考にしてください。
続きを見る



平行移動のやり方と公式の意味→符号を入れ替えて書き換えるだけで、グラフの問題がスラスラ解ける
まとめ


まとめ
接線の方程式を求めるためには、
- 導関数\(f’(x)\)を求めて、
- 微分係数\(f’(a)\)を求めて、
- 平行移動すればOK
一応接線の方程式の公式として、
と表すことはできますが、これは無理に暗記するよりも、紹介した3STEPを身に着ける方が実用的です。


またこの手順通りにすれば、接線問題はだいたいOK。
習うより慣れろ、たくさんの問題をこの手順で解いてみてください。
以上、「接線の方程式」についてでした。
チェック問題
例題
関数\(y= x^3+2x+2\)の\(x=3\)における接線の方程式を求めよ。
より、\(x=3\)における接線の傾きは
直線\(y=29x\)が、接点\((3,35)\)を通れば良いので、求める接線は
例題
三次関数\(y=f(x)=ax^3\)の接線が直線\(y=x-1\)であるとき、\(a\)の値と接点の座標を求めよ。
三次関数であることから、\(a\neq0\)。
接点を\(\left(t,at^3\right)\)とすると、微分係数は
つまり、直線\(y = 3at^2 x\)が接点\(\left(t,at^3\right)\)を通るように平行移動した
(※見切れている場合はスクロール)
は接線の方程式を表す。
\(y=x-1\)と比較すると、
を満たす。
\(a\neq0\)に注意すると、\(②\div①\)より、
②に代入して、
よって\(at^3 = \frac{1}{2}\)
以上より、
- \(a=\frac{4}{27}\)
- 接点の座標は\(\left(\frac{3}{2},\frac{1}{2}\right)\)









