平行移動のやり方と公式の意味→符号を入れ替えて書き換えるだけで、グラフの問題がスラスラ解ける

Today's Topic

関数$y=f(x)$のグラフを、$x$軸方向に$+p$、$y$軸方向に$+q$だけ平行移動したグラフは、

$$y-q=f(x-p)$$

と表せる。

小春

楓くん、平行移動って不思議よね？

ん、どこがだい？？

楓

小春

例えば$y=x^2$を$x$軸方向に$+3$動かすと、$y=(x-3)^2$になるじゃん？なんでマイナスになるんだろうなぁって。

なるほど、グラフのイメージと式が結びついていないってことだね。

楓

小春

だから今日は、平行移動をなるべく簡単に解説してほしいな！

OK、それじゃ今日は平行移動の公式の意味と、コツをマスターしていこう！

楓

こんなあなたへ

「二次関数の平行移動の意味がわからない」

「平行移動の公式が成り立つのはなんで？？」

この記事を読むと、この問題が解けるようになる！

関数$y=x\sin x$を$x$軸方向に3、$y$軸方向に-1平行移動したグラフの方程式を求めよ。
二次関数$y=\left(x+2\right)^2+4$の頂点の座標を求めよ。

答えは一番最後にあるよ！

楓

Contents

1 平行移動の公式
2 平行移動のイメージ
3 平行移動の練習問題
- 3.1 二次関数の平行移動
- 3.2 難しそうに見える関数の平行移動
4 平行移動｜まとめ

平行移動の公式

まずは公式からご紹介します。

平行移動の公式

関数$y=f(x)$のグラフを、$x$軸方向に$+p$、$y$軸方向に$+q$だけ平行移動したグラフは、

$$y-q=f(x-p)$$

と表せる。

小春

$x→x-p$、$y→y-q$って感じに書き換えるんだね。

平行移動は、横にいくつ、縦にいくつ動かすって動かし方をしている点にも注目だ。

楓

この公式の凄いところは、すべての関数に適用できるという点です。

例えば、関数

$$y=x^3-4x+1$$

を$x$軸方向（横）に$+6$、$y$軸方向に$+2$だけ平行移動すると、その方程式は

$$y\color{red}{-2}=(x\color{red}{-6})^3-4(x\color{red}{-6})+1$$

となります。

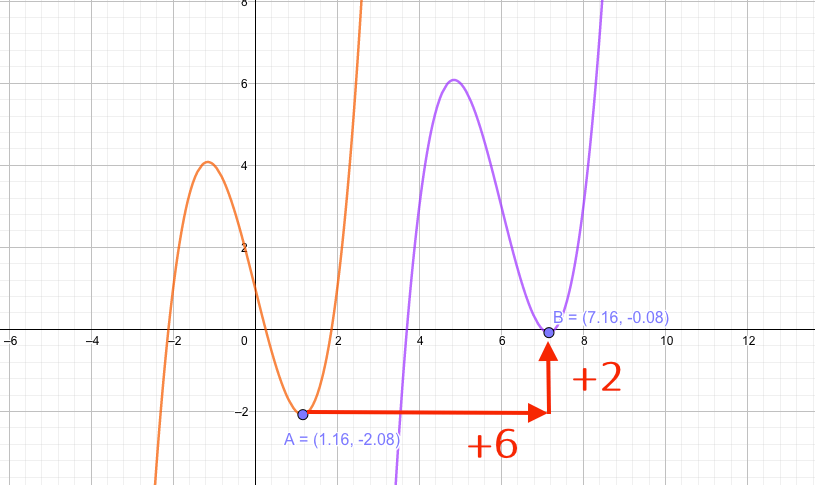
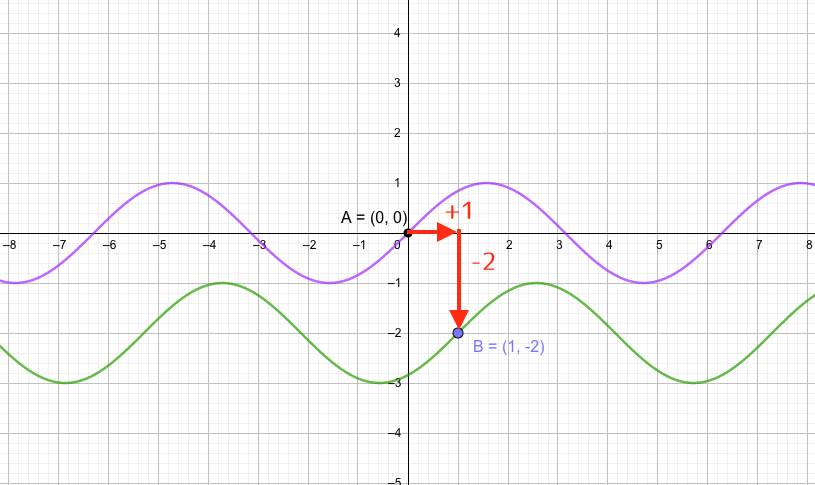
三角関数だって例外ではありません。

三角関数

$$y=\sin x$$

を$x$軸方向に$+3$、$y$軸方向に$-2$だけ平行移動すると、

$$y+2 = \sin\left(x-3\right)$$

となります。

小春

でもさでもさ、なんで横に＋3動かすって言っているのに、式では$(x\color{red}{-}3)$ってなるの？

それは、グラフ上の点をイメージする必要があるよ。

楓

平行移動のイメージ

ここでは、具体的に二次関数を例に考えていくことにしましょう。

そもそも数学では、線は点の連続として考えられます。

つまりグラフを平行移動させるという行為は、グラフ（線）を形成している全ての点を同じように動かすということに他なりません。

楓

この図では4つの点の移動の仕方がどれも同じことを言っているけど、実際は無数にある全ての点が同じ動きをするよ。

無数にあるなら全部書ききれないね・・・。

小春

楓

そうなんだ！そこで、放物線上のある1点に注目してみよう。

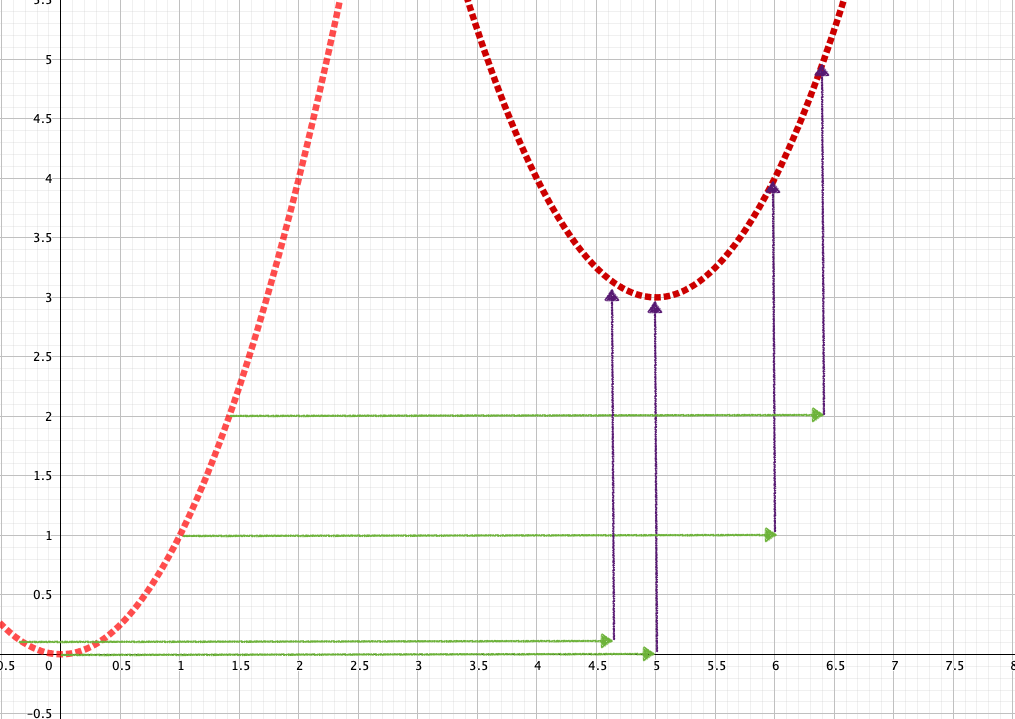
下の図は、ベースの放物線$y=ax^2$を横に$+p$、縦に$+q$だけ移動させた放物線について表したものです。

楓

$y=ax^2$上の適当な点$A(x,ax^2)$は、平行移動により点$B$に移動しているね。

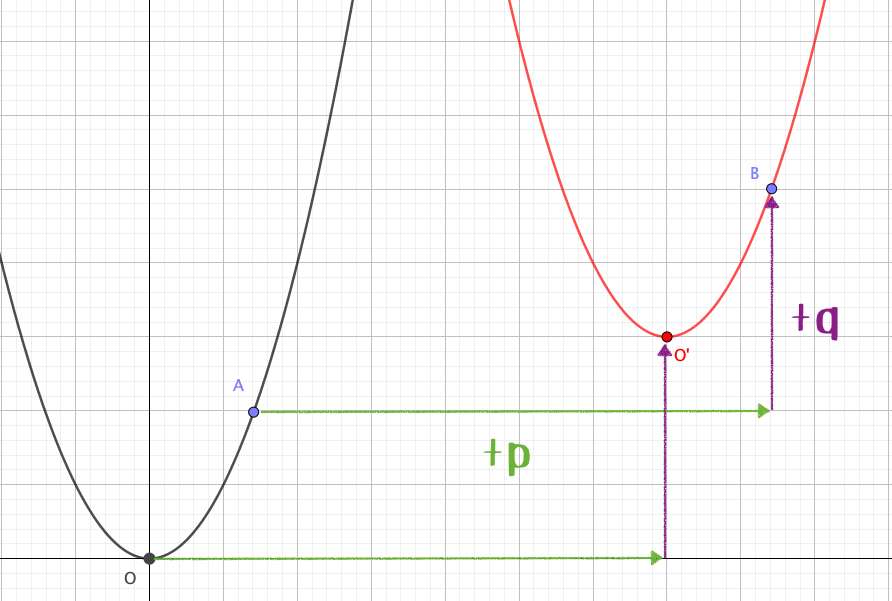
では移動した点Bの座標を$B(s,t)$としましょう。

このとき点Bの座標は

点Aの$x$座標から$p$だけ移動させたこと
点Aの$y$座標から$q$だけ移動させたこと

に着目すると、$B(x+p,ax^2+q)$と表せるはずですね。

すなわち、

$s=x+p$
$t=ax^2+q$

と表せますね。

小春

点Aの$x$座標に$+p$、$y$座標に$＋q$したんだね。

今まで$xy$座標上の点$(x,y)$においては、$y$を$x$で表したときグラフの方程式がわかりました。

それと同様に考えて移動した放物線上の点$B(s,t)$において、$t$を$s$で表したときグラフの方程式がわかると考えられます。

楓

ただし得られる方程式は横軸$s$、縦軸$t$の$st$座標のグラフだよ。

$s=x+p$でしたので、$x=s-p$と書き換えることができます。

この$x$を$t=ax^2+q$に代入してみましょう。

すると、

$$t=a\left(s-p\right)^2+q$$

となり、$t$を$s$で表すことができました。

楓

ただしこれは、先ほども言った通り$st$座標のグラフです。

$st$座標なんて一般には使わないので、$xy$座標に置き換えてあげる必要があります。

$st$座標では横軸$s$、縦軸$t$なので、$xy$座標の横軸$x$、縦軸$y$と比較して$s$を$x$に、$t$を$y$に書き換えてあげます。

すると、

$$y=a\left(x-p\right)^2+q$$

という移動した放物線の方程式が得られました。

$q$を移項することで、

$$y-q=a\left(x-p\right)^2$$

となり、形式的に

重要ポイント

$x$軸方向に$+p$、$y$軸方向に$+q$だけ平行移動すると、$x→x-p$、$y→y-q$に書き換えればよい

とまとめることができます。

小春

なるほど、つまりこういうことだね！

ポイント

『横に＋3動かすって言っているのに、式では$(x\color{red}{-}3)$ってなる』理由は、変形過程で移項が考えられているから

平行移動の練習問題

関数$y=f(x)$を横に$+p$、縦に$+q$平行移動すると、$y-q=f(x-p)$と表せる。

これを先ほどのイメージと結びつけておくと、グラフを想像することがかなり容易になります。

楓

グラフを想像する力は、数学力を上げるのに最も効果的な力だと思います。

では実際に具体例を見て、平行移動が意識できるとどれだけ簡単か見ていきましょう。

二次関数の平行移動

例題

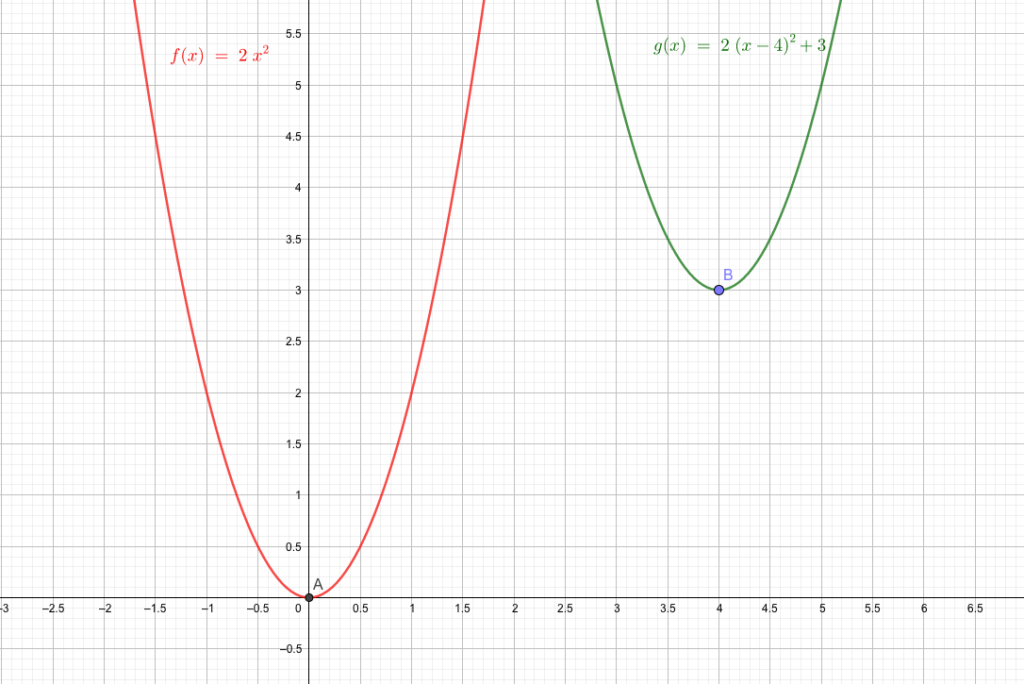
二次関数$y=2(x-4)^2+3$の頂点の座標を求めよ。

与えられた二次関数の$+3$を移項すると、

$$y-3=2(x-4)^2$$

となります。

これにより与えられた関数は、

$y=2x^2$を横に$+4$、縦に$+3$

と考えれば良いことがわかります。

楓

符号が逆になっている点に注意ね。

関数$y=2x^2$は頂点$(0,0)$なので、横に$+4$、縦に$+3$動かした関数の頂点は

$$(0+4,0+3)=(4,3)$$

となります。

実際に２つのグラフを描いてみると、

小春

確かに横に+4、縦に+3動いてるね。

難しそうに見える関数の平行移動

では、グロそうに見える関数を考えていきましょう笑

例題

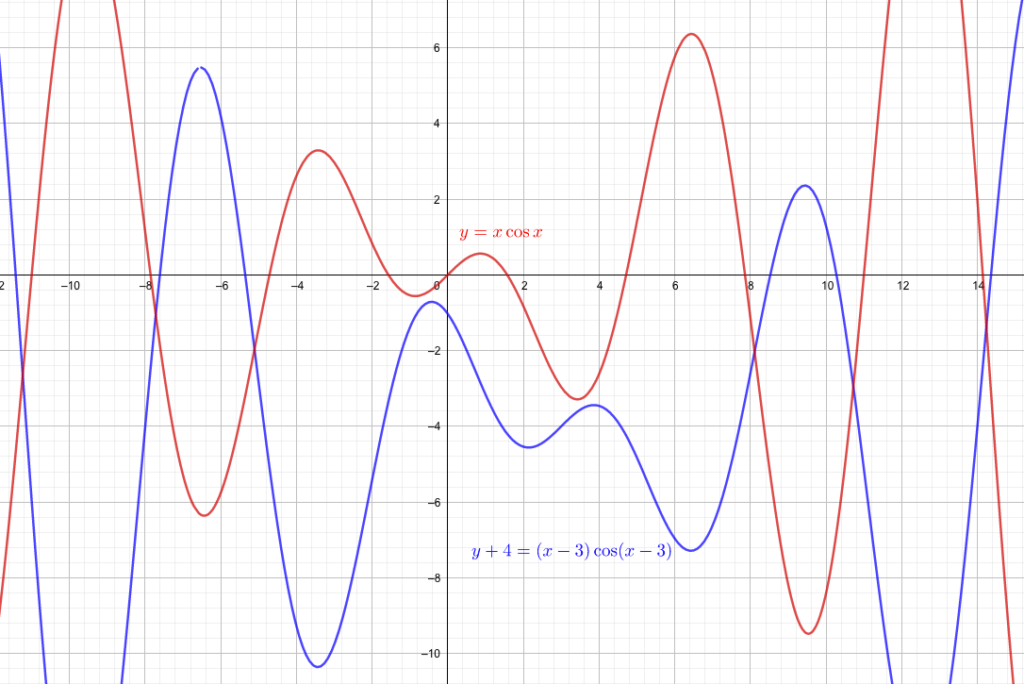
関数$y=x\cos x$を横に+3、縦に-4平行移動させたグラフの方程式を求めよ。

小春

関数$y=x\cos x$のグラフなんて想像できないよ・・・

でも、公式を使うと方程式を求めることができる。これが公式の良い点だね。

楓

平行移動の公式より、

$$y+4=(x-3)\cos (x-3)$$

実際にグラフを描いてみると、

小春

確かに平行移動している！

平行移動｜まとめ

楓

最後にまとめるぞ！

まとめ

関数$y=f(x)$のグラフを横に$+p$、縦に$+q$平行移動させたとき、$x$を$x-p$に、$y$を$y-q$に書き換えてあげればOK
符号が変わるのは、導出過程で移項が使われているから
どんな関数にも使える

平行移動の考え方を知っていると、方程式の見方が変わります。

例えば、$y-3=\cos(x-\frac{\pi}{3})$という方程式が出されても、

$y=\cos x$を横に$+\frac{\pi}{3}$、縦に$+3$ズラしただけだな

と見抜ければ、問題が解きやすくなったり、心理的ハードルが下がったりします。

これから先、いろんな問題に出会うと思いますが、関数や方程式の問題では、ぜひ平行移動を意識して見てください。

以上、「平行移動について」でした。

最初の答え
Q. 関数$y=x\sin x$を$x$軸方向に3、$y$軸方向に-1平行移動したグラフの方程式を求めよ。

A.$y+1=(x-3)\sin(x-3)$

Q.二次関数$y=\left(x+2\right)^2+4$の頂点の座標を求めよ。

A.$y=x^2$の頂点は$(0,0)$
$y-4=(x+2)^2$は$y=x^2$を