Today's Topic
関数とは\(x\)の値を1つ定めると、\(y\)の値が1つ定まる関係のことをいい、一対一・多対一対応がこれに当てはまる。
関数かどうか判断するためには、グラフを考えて\(x\)軸に垂直な直線との交点が1つであるか確かめれば良い。



この記事を読むと、この問題が解ける!
- \(x=2^y\)は関数であると言えるか。
- 方程式\(x^2+y^2=1\)は中心が原点の、半径1の円を表す。この方程式は関数として適切か?

関数の定義
まずは関数の定義をみてみましょう。
定義
『\(y\)が\(x\)の関数である』とは、\(x\)の値を1つ決めたとき、\(y\)の値がいつでもただ1つに決まる関係のこと。
関数の説明をする際に、自動販売機の例がよく用いられますが、全然わかりやすくないと思うので、ここでは純粋に数学の集合だけを用いて考えていきましょう。
一対一対応とは
2つの変数\(x\)と\(y\)を使って考えていきましょう。
この2つの変数には、今は特に決まりがなく、ただ単に\(y\)の値は\(x\)の値によって変化するというルールのみが存在するとします。
例えば\(y=2x\)という方程式は、「\(y\)の値は\(x\)の値を2倍したもの」ということを表しており、\(x\)の値が変化すれば、\(y\)の値も当然変化しますね。


この\(y=2x\)という方程式において、次のような状況が存在するか考えてみましょう。
ある\(x\)の値を代入したところ、\(y\)の値が異なる2つの値が求められた


このように、\(x\)の値を1つ定めると、\(y\)の値が1つだけ定まる状況を一対一対応といいます。
一対多対応とは
では\(x\)を1つ定めたときに、\(y\)の値が2つ以上決まる場合はあるのでしょうか?
実はこの世界には無数にあります。
例えば方程式\(y^2 = x\)を考えてみましょう。
これは\(x\)の値が4のとき、\(y=2\)となりますね。
しかし\(y=-2\)の場合でも、\(y=2\)のときと同様に\(x=4\)となりませんか?
ちゃんと
ある\(x\)の値を代入したところ、\(y\)の値が異なる2つの値が求められた
という状況が起きていますね。

このように、1つの\(x\)に対して、2つ以上の\(y\)の値が定まる状況を一対多対応といいます。
多対一対応とは
\(x\)の値を1つ定めると、\(y\)の値が1つに定まる一対一対応。
\(x\)の値を1つ定めると、\(y\)の値が2つ以上定まる一対多対応。
実はもう1つ、多対一対応というものがあります。
これは\(x\)の値を複数当てはめても、\(y\)の値が1つに定まる状況を指します。

\(y=0x+5\)はまさに多対一のいい例でしょう。
\(x\)にどんな値を代入しても、\(y\)の値は全く変化せず5のままですね。
関数は一対一、多対一のこと
ここで簡単にまとめると、図のようになります。
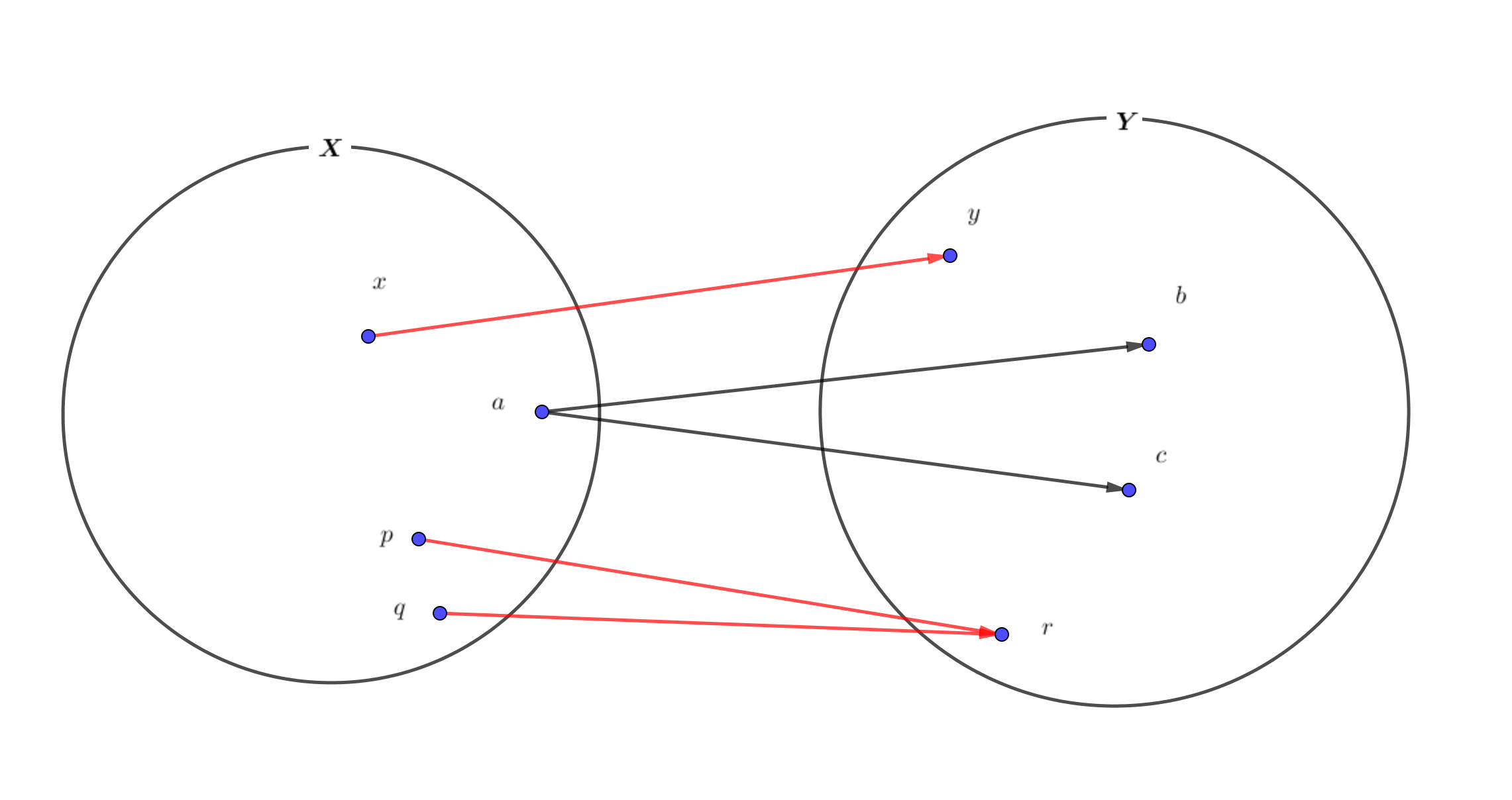
- \(x\)と\(y\)の関係:一対一対応
- \(a\)と\(b,c\)の関係:一対多 対応
- \(p,q\)と\(r\)の関係:多対一 対応


ここで、もう一度関数の定義を見返してみましょう。
定義
『\(y\)が\(x\)の関数である』とは、\(x\)の値を1つ決めたとき、\(y\)の値がいつでもただ1つに決まる関係のこと。
つまりこの3つのうち、一対一、多対一対応だけが関数の定義を満たしますね。

そして集合\(X\)に属する値のことを独立変数、集合\(Y\)に属する変数のことを従属変数と言います。
具体的には『\(y\)が\(x\)の関数である』としたとき、\(x\)のことを独立変数、\(y\)のことを従属変数と呼ぶわけです。




関数はグラフで捉えるとわかりやすい
今回一対一、一対多、そして多対一を説明する中で利用した
- $$y = 2x$$
- $$y^2 = x$$
- $$y = 0x+5$$
の3つをそれぞれグラフで見ていこうと思います。
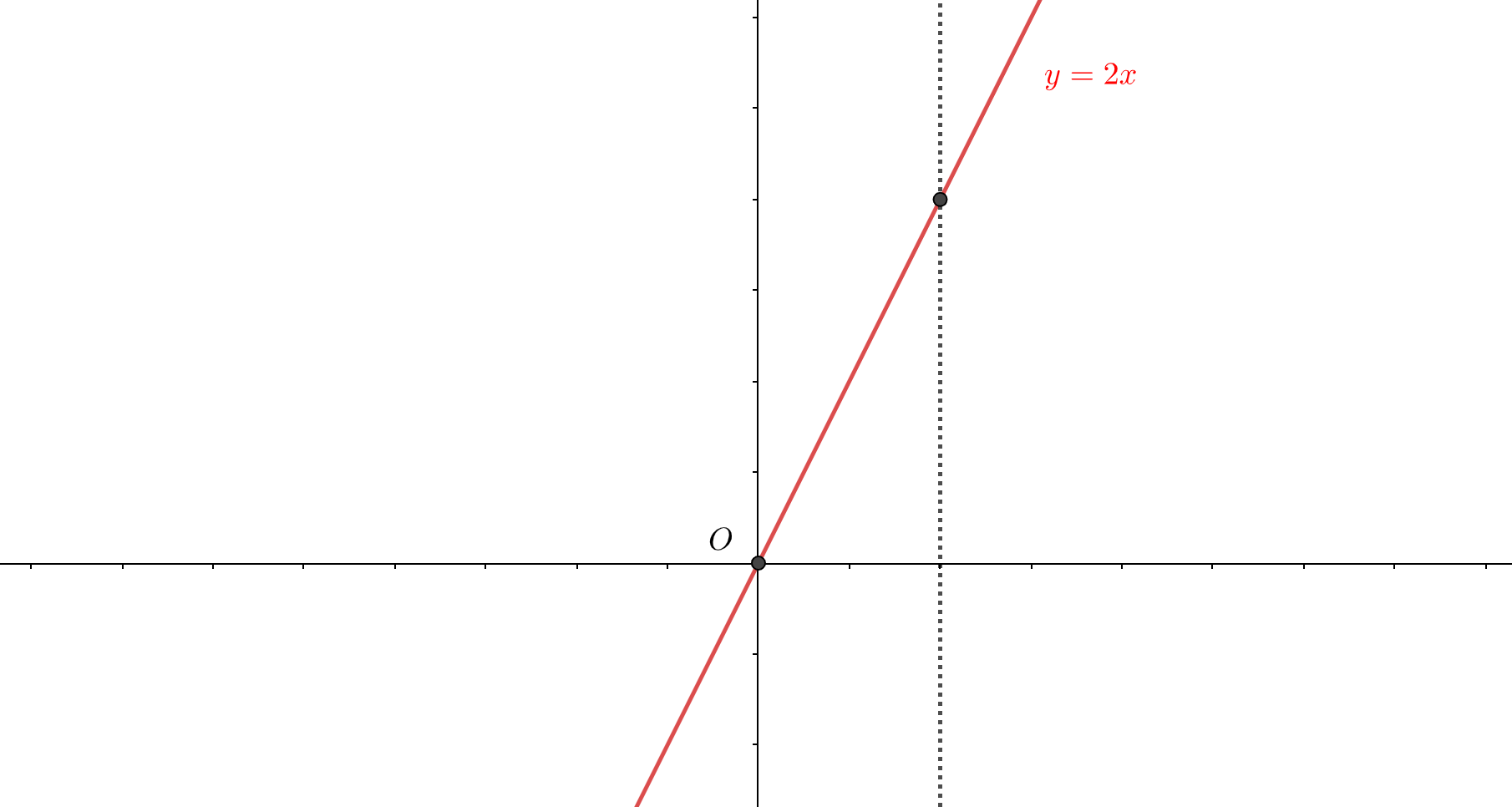
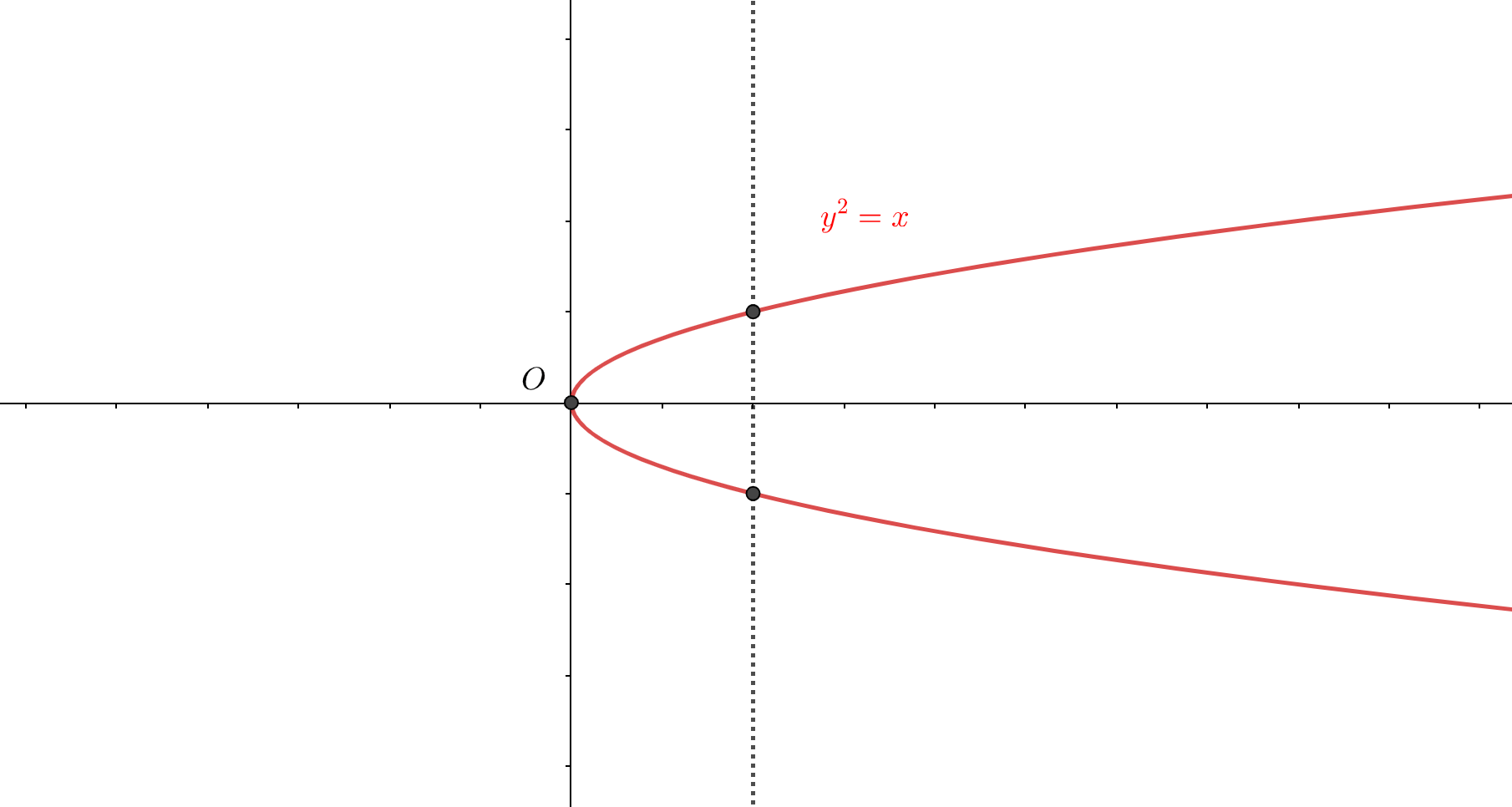
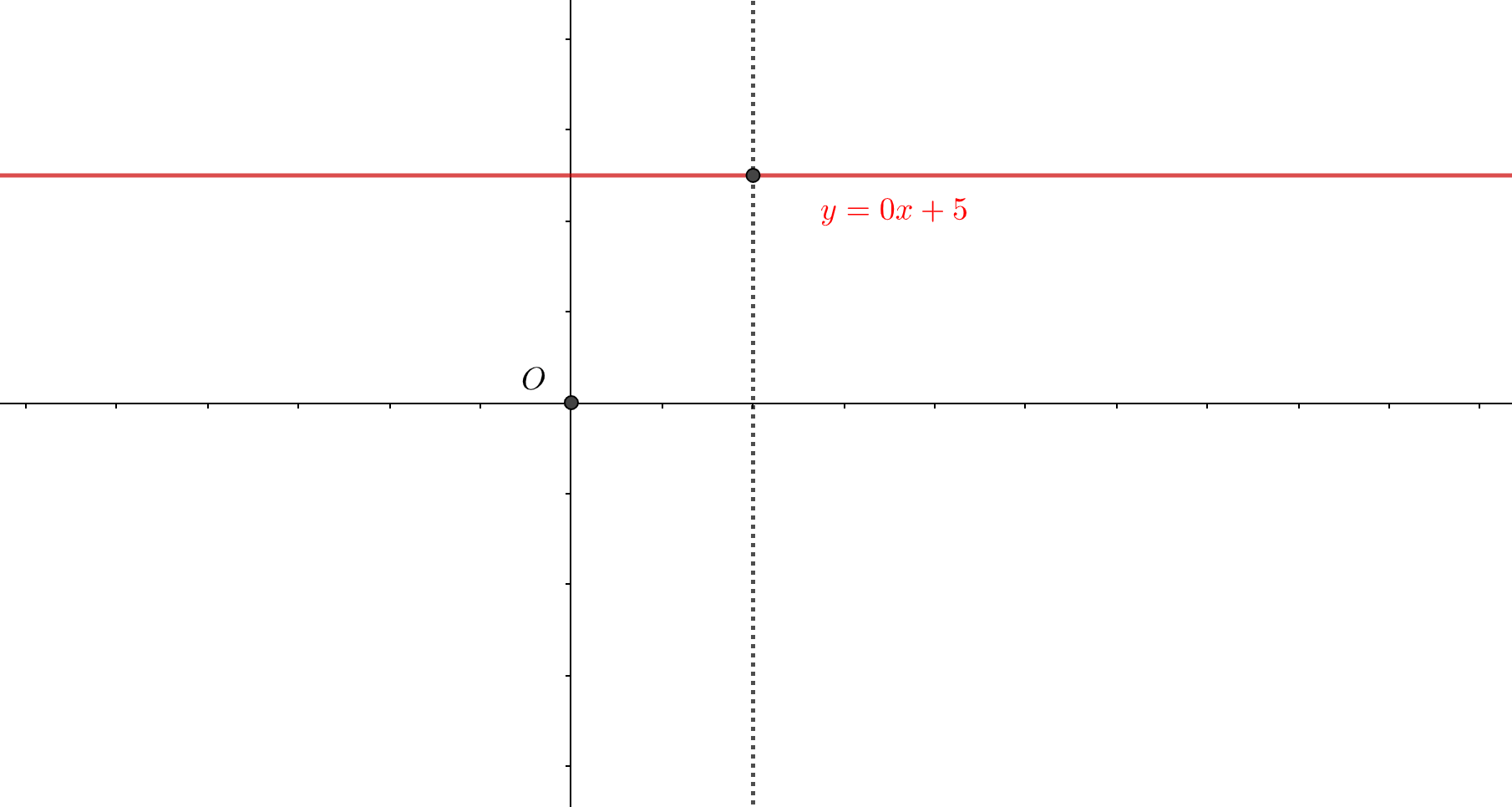
この3つのグラフを眺めたとき、あることに気づきませんか?






\(x\)軸に垂直な直線は方程式\(x = a\)のように表せますが、グラフ中の点線はまさしくこの\(x=a\)を表しています。
つまりこれまで考えていた\(x\)の値を1つ決める、とはグラフにおいては\(x\)軸に垂直な直線を一本決めるということに他なりません。
これにより、\(x\)軸に垂直な直線とグラフの交点が\(x\)に対応する\(y\)の解の個数を表しており、この個数が2個以上ある場合は、すなわち一対多を意味するため関数ではないことがわかります。
関数かどうか判断するためには、グラフを考えて見れば良い。
まとめ

まとめ
関数とは\(x\)の値を1つ定めると、\(y\)の値が1つ定まる関係のことをいい、一対一・多対一対応がこれに当てはまる。
関数かどうか判断するためには、グラフを考えて\(x\)軸に垂直な直線との交点が1つであるか確かめれば良い。
関数は高校数学ではいくつかの種類出てきますが、関数の議論は大学数学まで続く重要な内容です。
中学校の段階で曖昧でも、高校数学以降その意味を疎かにしていると数学の魅力が半減以下になるといっても過言ではありません。
ぜひ遠回りと思わずに、確実に歩いてみてください。
以上、「関数について」でした。
チェック問題
例題
\(x=2^y\)は関数であると言えるか。

\(x\)が1のとき、\(y\)の値は指数法則より0となりますね。
その他\(x=3\)や\(x=7\)のときなどを考えてもいいですが、正直あまりピンとこないのではないでしょうか。
そこでいっそ、絶対にこの方程式が成り立たない場面を考えてみましょう。
すると、例えば\(x=-1\)など負の値を取るとき、2を何乗しても負の値にはなりませんのでこの方程式は不成立ですね。
つまり\(x\)の値を1つ定めているにもかかわらず、それが負の数である場合、\(y\)の値は1つも定まらないということになります。
よってこれは関数ではありません。
例題
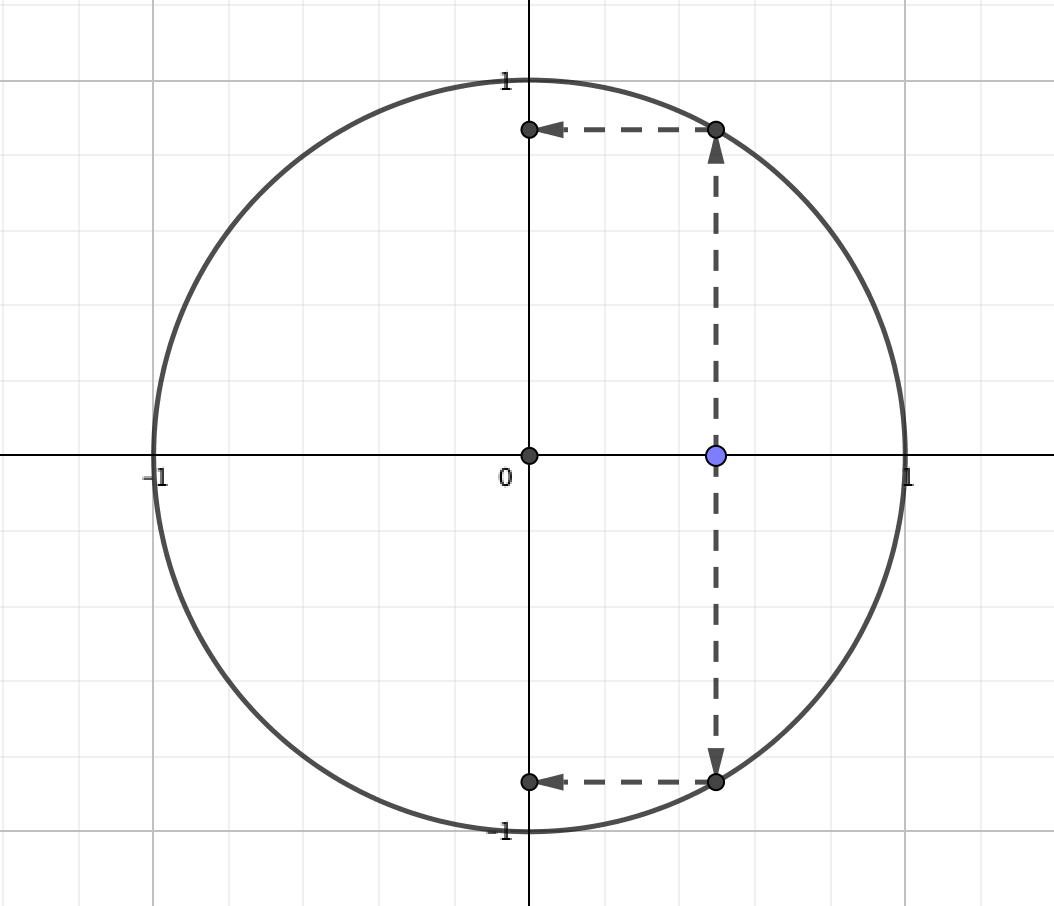
方程式\(x^2+y^2=1\)は中心が原点の、半径1の円を表す。この方程式は関数として適切か?
これはせっかくなのでグラフから考えてみましょう。