【指数方程式/指数不等式】より簡単な方程式に変形する2つの方法と満点を取るテクニック

 

 

 

 

指数方程式の方針と、解法の見極め方

 

のように、指数に変数\(x\)を持つような方程式を指数方程式と言います。

 

指数方程式は、例えば上記のように\(x=3\)とすぐにわかるような事例は少なく、ほとんどの場合、そのまま解くのは至難の技です。

 

そこで、指数方程式を解く解法が編み出されたわけですが、それが

の2つです。

この2つさえ抑えておけば十分です。

 

ただし、解法を覚えて普通に解くのではなく、必ず指数関数のグラフの形を意識しましょう！

下に具体例を示しますが、トラップにかかる危険性を可能な限り抑えられます。

また、逆に言えば指数関数を意識するいい練習にもなりますので、この機会を活用しましょう。

 

【解法1】底を揃えて、文字に置き換える

 

先ほど紹介した指数方程式

 

これは\(x=3\)とパッと出てくると思いますが、それはなぜでしょう。

 

おそらくこの指数方程式を頭の中で、次のように訳しているからではないでしょうか。

 

そして頭の中で8は2の3乗であることを思い出して、\(x=3\)が導かれているのでしょう。

 

つまりこの流れを式で表すとこのようになります。

 

これが解法の1つ目、底を揃えて指数を比較するという手法です。

 

これを応用すると、少し複雑な指数方程式も、二次方程式などのより簡単なものに変えることができるので、たやすく解けるようになります。

具体例を見てみましょう。

 

 

 

この方程式をサッと眺めてみると、\(4^x\)と\(2^x\)があるので、左辺は底を2で揃えることができそうです。

 

ここで\(2^x = t\)というように別の文字に置き換える、いわゆる置換を行います。

すると、左辺は

となるので、提示された指数方程式は、二次関数

に帰着できるようになったわけです。

 

指数に変数が含まれている項に対して、底を共通の数に揃えて適当な文字に置換すると、指数方程式から、これまでに習った簡単な方程式に変換することができる！

 

この\(t\)で表された二次方程式を解くと、

と求められますが、これは実は間違いです。

 

ここで念をむちゃくちゃ押していた指数関数のグラフを思い出してみましょう。

参考【指数関数のグラフと性質】これだけはサッと思い出したい、超重要な6つの性質

 

 

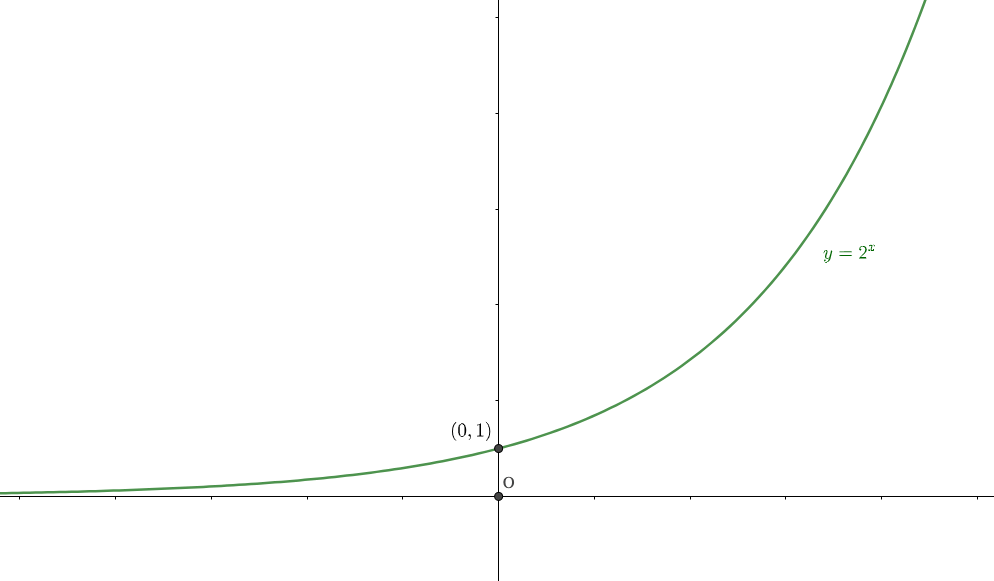
じ〜っと眺めてみると、わかりますね？

そうです、\(y=2^x\)はどんな\(x\)の値をとっても、絶対に\(y\)の値は0を下回ることはありませんでしたね。

 

では\(t=2^x\)と置いたのであれば、、、

 

よって、\(t =1\)、すなわち\(2^x = 1\)が求めるべき最終的な方程式になります。

そしてここでも底を2に揃えることで、\(1 = 2^0\)なので

となり、答えは\(x = 0\)となります。

 

【解法2】底が揃わない場合、対数をとる

 

 

次はこの例題をやってみましょう。

いきなり解く前に、まずはちょっと眺めてみましょうか。

 

左辺の底が5なので、右辺も5で揃えられれば、先ほどの手法がそのまま使えますね。

しかし、

となるため、2だけが底を5に揃えることができませんね。

 

このように左辺と右辺の底が一定の数にそろえられない場合は、対数を取る手法が有効です。

このとき取るべき対数についてですが、\(x\)などの変数が含まれている指数が残るように取りましょう。

 

両辺に底が5の対数をとると、

 

 

のようになりますね。

 

参考log(ログ)って何？常用対数、自然対数とは？対数を徹底解説！！

 

これらをつなげると、

となり、普通の一次方程式に持ち込むことができました。

整理してあげると、

となりましたね。

 

底が揃わない指数方程式を解くためには、指数に変数が含まれている項の底で対数を両辺にとり、指数方程式から一次方程式などの簡単な方程式の戻せば良い。

 

今回はたまたま指数関数のグラフを意識しなくても良さそうですね。

ただ問題を解く前に必ず、指数関数のグラフを意識して定義域などをしっかり把握しておくクセをつけておいてください。

 

【油断大敵】絶対にグラフをすみっこに書いて！

 

ここまでグラフグラフと言ってきましたが、

実際あんまり効果なくね？

とナメ腐っている方もいると思うので、ひやっとする問題を出してみましょう。

 

 

 

まずは普通に式変形をしてみます。

底を揃えたいって気持ちになるのは、お察しの通りです。

 

まだ式変形は施せますが、ここまでで実は十分です。

 

式を和訳してみると、

となっていますね。

 

ここで\(y=\left(\frac{1}{2}\right)^x\)のグラフを思い浮かべてみましょう。

厳密なグラフなんかどうでも良くて、こんな感じで十分です。

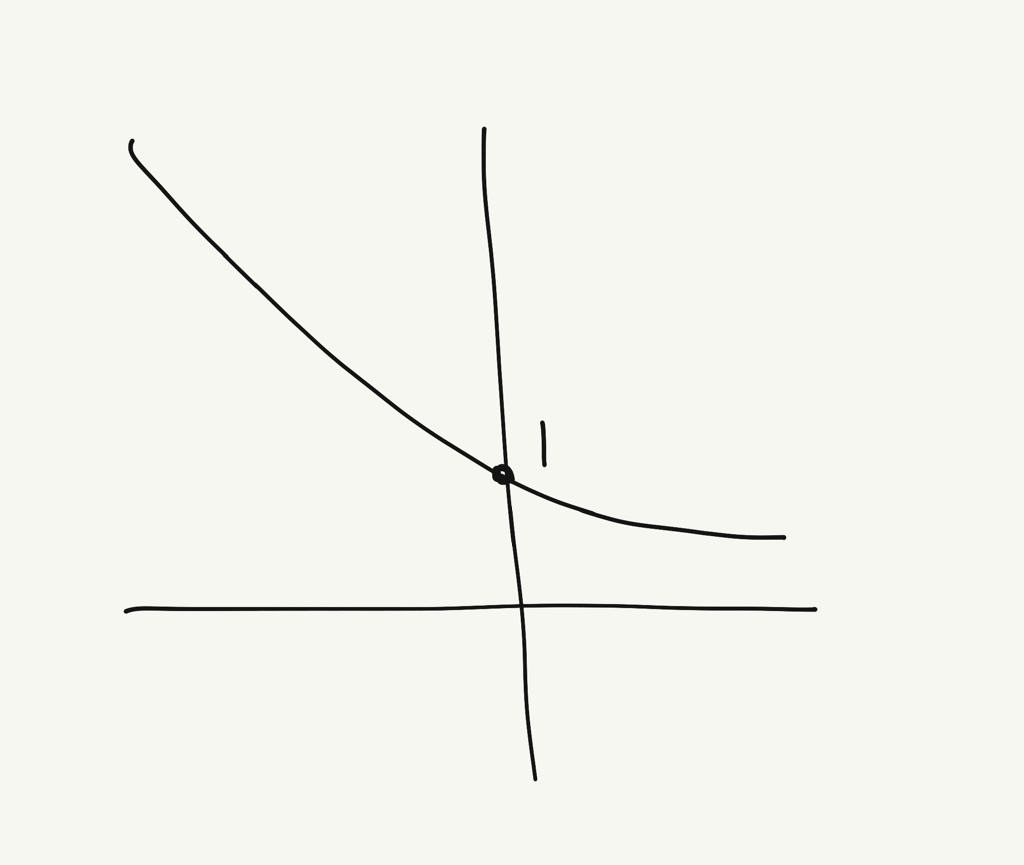
参考【指数関数のグラフと性質】これだけはサッと思い出したい、超重要な6つの性質

 

注意して欲しいのはグラフの形です。

底\(\frac{1}{2}\)は1よりも小さいので、グラフはベースの指数関数\(y=2^x\)が\(y\)軸をつまんでひっくり返したような形になりましたね。

 

このグラフに、

の位置関係を描いてみるとこのようになります。

 

 

 

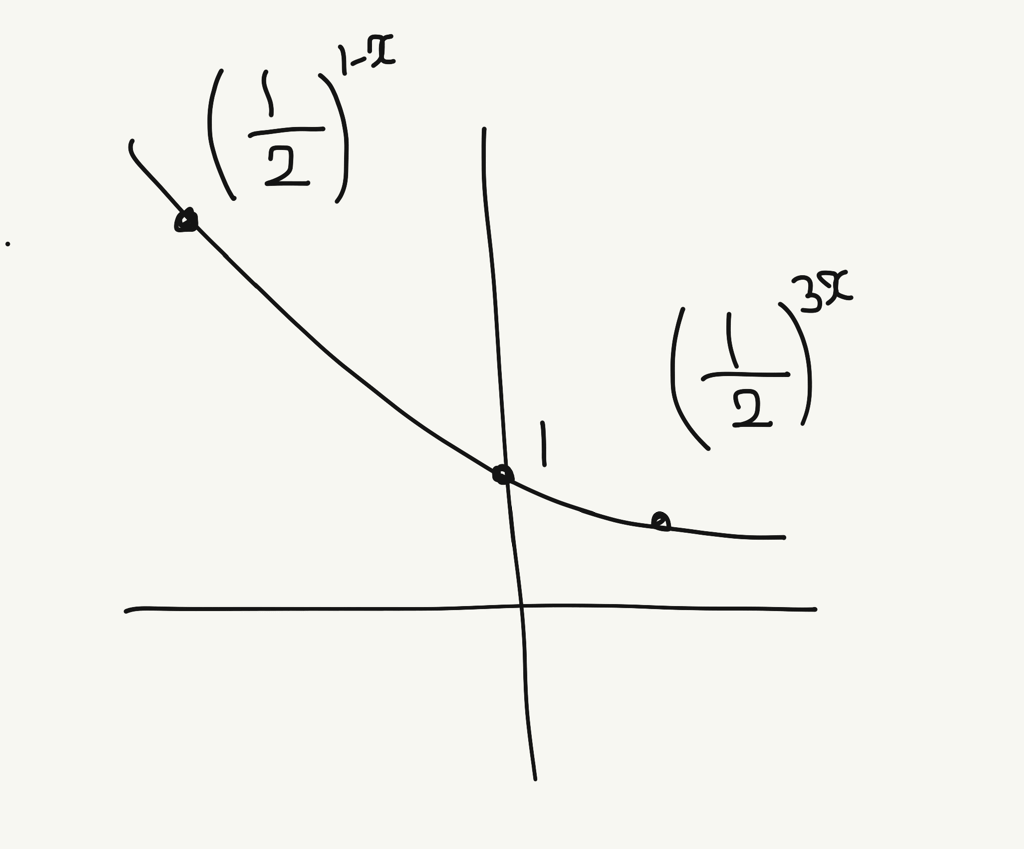
これにより、与えられた不等式

に対して、考えるべき不等式が

にまで絞ることができました。

 

あとはこれを整理すればよく、難しい理論やまどろっこしい式変形などせずとも、式変形だけで得るべき解が

と求められたのは、かなり効率的ですね！

 

指数方程式、指数不等式はどちらも、変数が指数に含まれていることが難しくなっている1番の原因です。

なので、変数を指数から下ろし、底に持ってくる、すなわち普通の方程式・不等式のように扱えればなんでもいいわけです。

それが式変形を使おうが、グラフの形を見ようが、どちらでも。

 

ただ計算ミスをせずに

「見ればわかるじゃん」

と簡単にまとめられるグラフの方が、やはり解法的にはスマートですね。

 

まとめ

 

 

何度も言いますが、指数方程式は変数に指数が含まれていることが大きな問題です。

変数を指数から消すことが今回扱った2つのテクニックのテーマであり、そこから先の議論はグラフを意識して進めていった方が安心です。

 

2つの解法パターンだけでなく、ぜひグラフを意識する習慣を身につけていきましょう。

以上、「指数方程式・指数不等式の解き方について」でした。

 

チェック問題

 

指数方程式は、指数に変数が含まれていることが難しい理由でしたので、まずは変数部分の底を揃えて、より簡単な方程式に持ち込みたいなあという意識をしていきましょう。

 

変数\(x\)が含まれている\(\left(\frac{1}{9}\right)^{x}\)と\(\left(\frac{1}{3}\right)^{x+1}\)は、共に底を3で統一することができそうですね。

 

さっきやった例では、底を\(\frac{1}{2}\)のような分数に揃えましたが、わざわざ分数に揃える必要はなく、今回の3のような整数の底に持ち込んでもOK。

 

つまり与えられた方程式は、4を両辺から引いてあげれば

のように式変形できるわけです。

 

ここで、\(t = 3^{-x}\)と置くと、方程式は

のようになりますね。

 

ただしグラフを考えてみると、\(y=3^{-x} = \left(\frac{1}{3}\right)^x\)は次のようなグラフになるはずです。

 

解の公式を用いると、先ほどの方程式の解\(t\)は、

のように求められますが、\(t> 0 \)の条件を考えると、

のみ解として適切であることがわかります。

 

最後は優しさで整理してあげて、

 

 

この不等式、よく見てみると底が2、もしくは\(\frac{1}{2}\)で揃えられそうですね。

わざわざ\(\frac{1}{2}\)に揃えるのも手間ですし、今回は2で揃えてみましょうか。

 

であることを考えると、与えられた不等式は

を考えれば良さそうです。

 

ここで、底が2の指数関数\(y=2^x\)のグラフを考えると、このようになっています。

 

\(x\)の値が大きくなるほど（つまりグラフの右側になるほど）、\(y\)の値は大きくなりますね。

 

よって、指数不等式

の大小関係は、単に指数だけ着目すればよく、グラフの形から\(y\)の値は

の順に大きくなっていく（つまり右側に向かっていく）ってことですね。

 

全ての辺に\(-\frac{1}{2}\)をかけてあげると、不等号の向きが逆転しますので、

 

全ての辺に3を加えてあげれば、

が得られました！