【収束・発散の速さ】絶対に覚えておきたい極限の裏公式｜見た瞬間に極限がヒラメク！

Today's Topic

いろいろな関数が組み合わさった関数の極限を求めるためには、各関数の極限の発散・収束の速さに着目して解けば良い。

小春

結構いろんな極限をこれまでみてきたから、私もいろんな問題解けるようになったよ！

おっ、やったね！

楓

小春

ただ数Ⅲの問題のほとんどは『いろんな関数の合体した関数』だから、ちょっと極限求めるの大変なんだよね。。。

じゃあ今日は、極限を解く力をもうワンステップ高める裏公式を教えるね！これさえ知っとけば一瞬で見抜けるよ！

楓

この記事を読むと、この意味がわかる！

$$\lim_{x\to +0} x^2\log x$$
$$\lim_{x\to\infty} \frac{\left(e^x-1\right)\left(e^x+2x\right)}{x^2-e^{2x}}$$

楓

答えは最後に扱うよ！

Contents

1 【これだけ知っておけばOK】発散の速さの関係性
2 練習問題
3 【証明】（一度はやって欲しい）発散の速さの証明
4 【まとめ】

【これだけ知っておけばOK】発散の速さの関係性

今回は3種類の基本的な関数

べき関数
指数関数
対数関数

の収束・発散について考えてみましょう。

結論から述べると次のような関係性が成り立ちます。

ポイント

小春

は、速さ？

例としてべき関数$y=x^3$と指数関数$y=3^x$のグラフを見比べてみましょう。

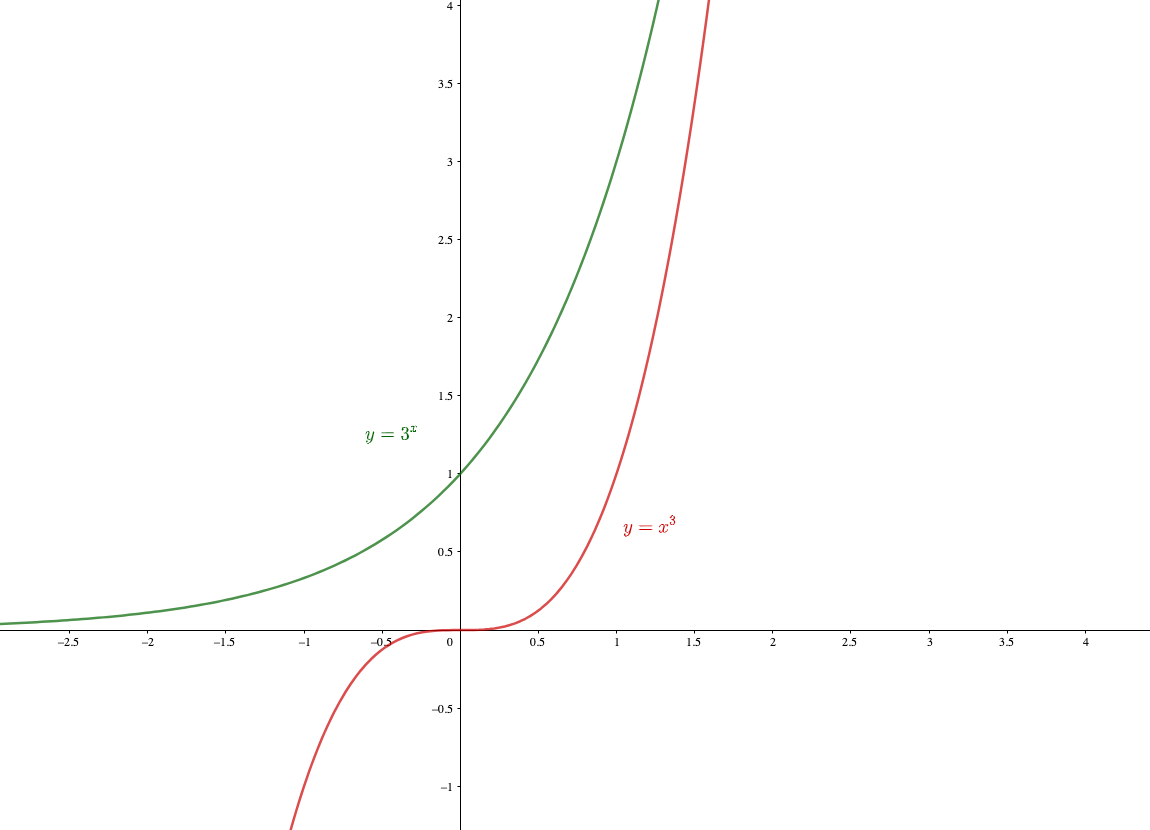
$x$の値が大きくなるほど、べき関数も指数関数も$y$の値が増加していますが指数関数のほうが$y$の値が爆発的に大きくなっていますね？

例えば$x=10$のときを考えてみると、

べき関数$y=10^3=1000$
指数関数$y=3^{10}=59049$

と圧倒的な差がありますね。

つまり発散の速度が速いほど、爆発的に$y$の値が増加することを意味しています。

楓

収束の場合は、速度が速いほど急激に値が収束することを意味するよ！

これにより、次のような複雑な関数の極限がカンで求められるようになります。

例題

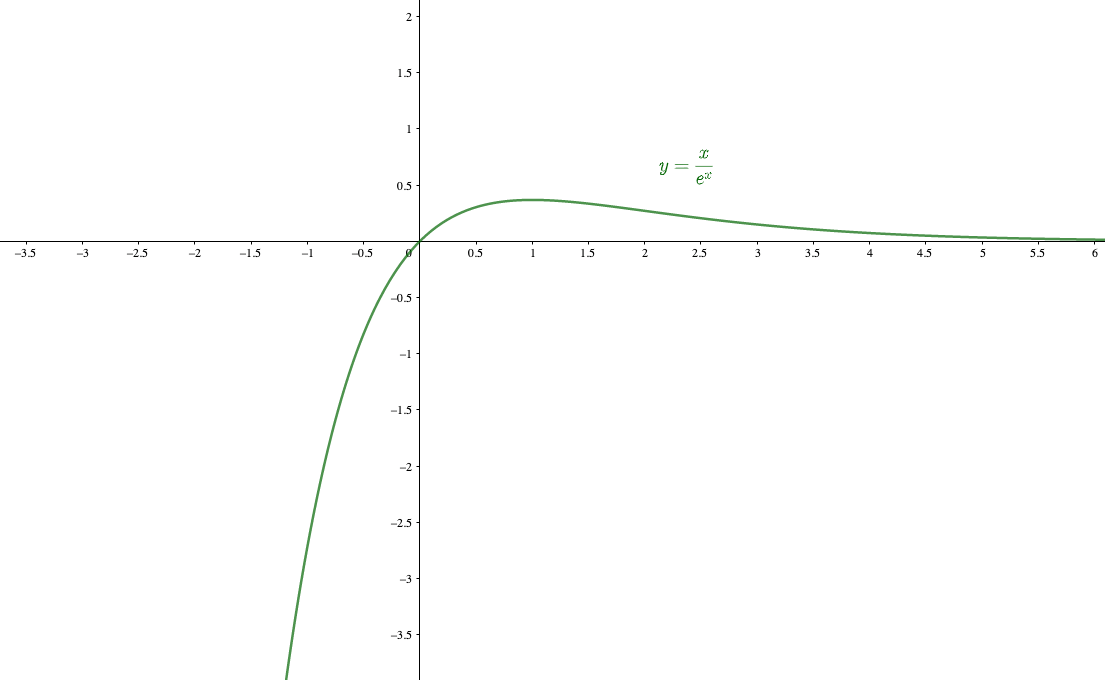
$$\lim_{x\to\infty}\frac{x}{e^x}$$

べき関数$x$に対して、指数関数$e^x$は爆発的に値が増加します。

よって$x\to\infty$においては、分子に対して分母の方が圧倒的に値が大きくなっていくので、次第に$\frac{定数}{\infty}$と同じような状況になるため

$$\lim_{x\to\infty}\frac{x}{e^x}=0$$

とみなすことができます。

実際のグラフ

小春

発散がより速い関数が分母にいると、収束しやすくなるんだね！

練習問題

収束・発散の速さをもう少し意識しやすいくするため、3つ例題を見ていきましょう。

例題

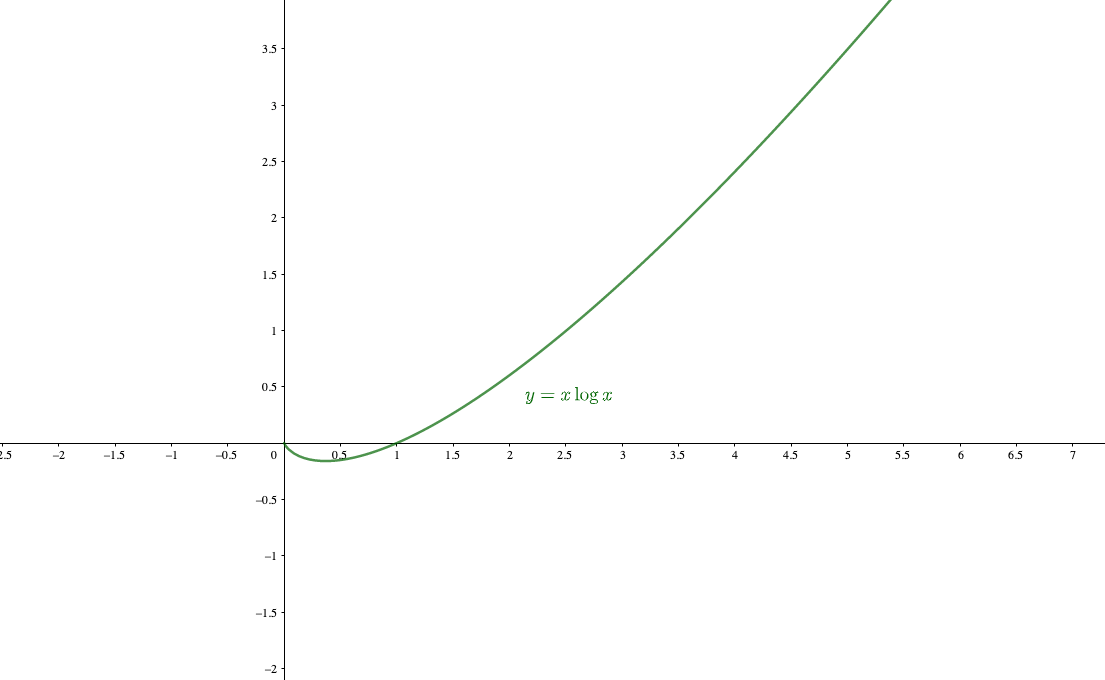
$$\lim_{x\to +0}x\log x$$

$y=x$と$y=\log x$の0付近のグラフを考えると、次のようになっています。

楓

べき関数の方が、対数関数よりも発散・収束のスピードが速いんだったね！

グラフを見てみるとわかるとおり、$x\to +0$を考えると$y=x$は急激に0に近づくのに対して$y=\log x$はノロノロと$-\infty$に向かっています。

具体的に$x = 0.000001$のときを考えてみると、$y=x$はほぼ0に近づいているのに対して、$y=\log x = -13.815\cdots$と全然$-\infty$に向かっていません笑

そのため$x\log x$は$0\times 定数$と同じような状況になってしまうので、

$$\lim_{x\to +0}x\log x =0$$

であることが分かります。

実際のグラフ

例題

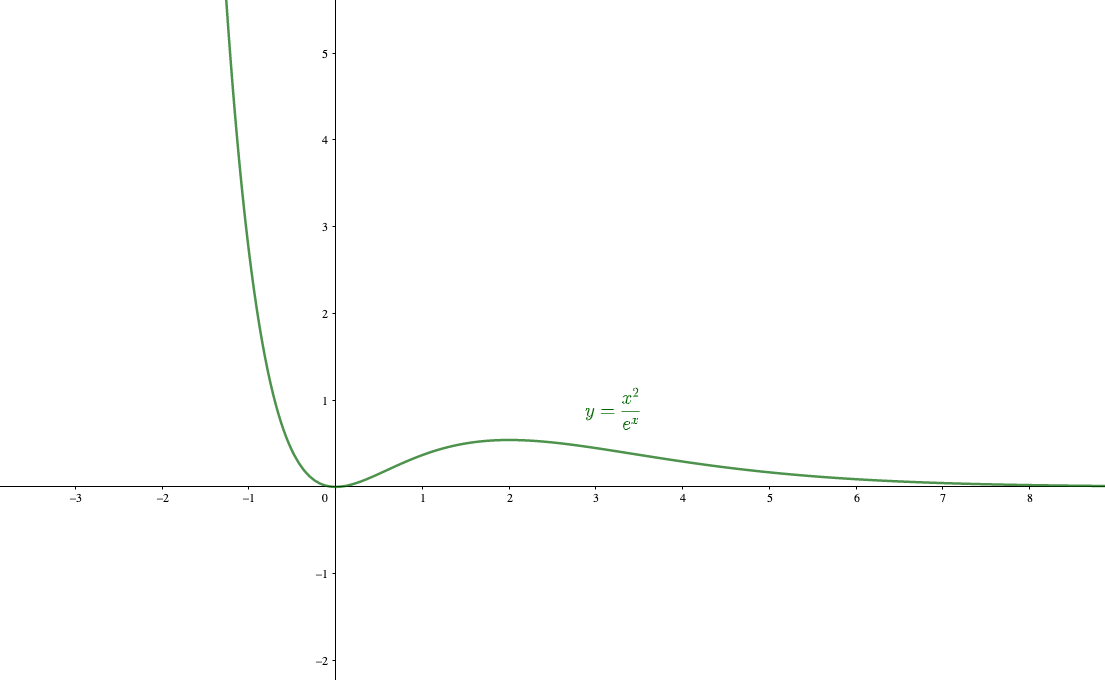
$$\lim_{x\to \infty}\frac{x^2}{e^x}$$

べき関数と指数関数は、指数関数のほうが発散・収束のスピードが速いんでしたね。

実際に$y=x^2$と$y=e^x$のグラフを見てみると

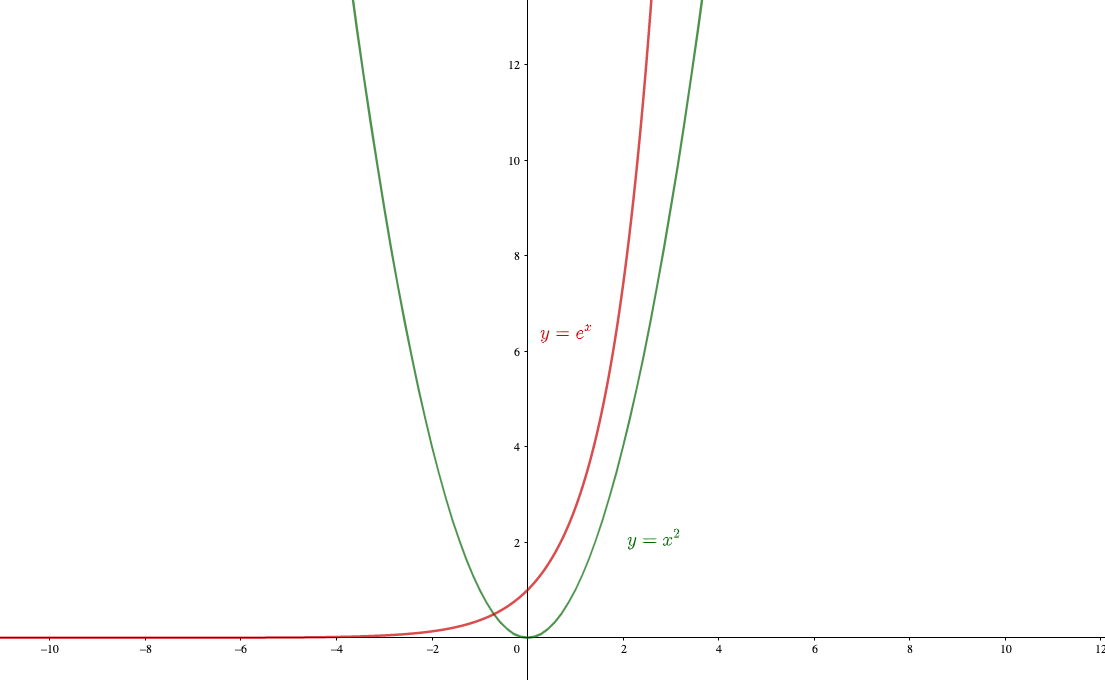
となっており、$y=x^2$がノロノロと$\infty$に向かう中、$e^x$はビュンッと$\infty$に発散しています。

よって$\frac{定数}{\infty }$のような状態になっているので、

$$\lim_{x\to \infty}\frac{x^2}{e^x} =0$$

と分かります。

実際のグラフ

例題

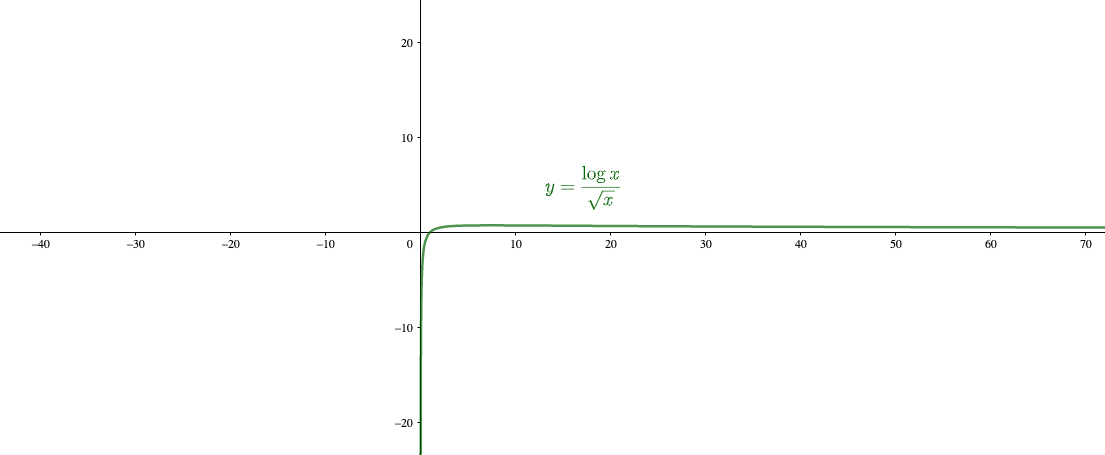
$$\lim_{x\to \infty}\frac{\log x}{\sqrt{x}}$$

ルートが出てきて戸惑うかもしれませんが、

$$\sqrt{x} = x^{\frac{1}{2}}$$

と変形すると、べき関数とみなせます。

べき関数の方が、対数関数よりも発散スピードが速いので$\frac{定数}{\infty}$と同じような状態です。

よって、

$$\lim_{x\to \infty}\frac{\log x}{\sqrt{x}}= 0$$

となります。

楓

グラフを使わなくてもパッとわかるね！

実際のグラフ

【証明】（一度はやって欲しい）発散の速さの証明

このべき関数、指数・対数関数の収束・発散の速さについては、基本証明なしで使ってもOK。

ただ証明が「一回経験しないと思いつかない」という、童貞殺しの証明なので一回は経験しておきましょう。

楓

ここからは発散の速さに着目したよくある証明を扱うよ。

ここでは具体的に、

$$\log x,\ x^a\ (a>0),\ e^x$$

の発散の速さについて証明していきたいと思います。

発散がより速い関数が分母にいると、その関数は収束しますので、ゴールとしては

$$\lim_{x\to \infty}\frac{x}{e^x}=0\ \cdots ①$$
$$\lim_{x\to \infty}\frac{\log x}{x}=0\ \cdots ②$$

を示せればOKということになります。

手順としては①→②の順で示すわけですが、この①がかなり童貞殺しとなっています。

結論から言うと、はさみうちの原理に持ち込みたいのですが、そのために

$$e^x > \frac{x^2}{2}\ (x>0)$$

を示します。

小春

な、なんで・・・

一回証明を見てもらった方が早いかも。

楓

$f(x) = e^x - \frac{x^2}{2}$とおくと、$x>0$のとき

$$f'(x) = e^x - x ,\ f''(x) = e^x-1 > 0$$

よって、$f'(x)$は単調増加することがわかるので、

$$f'(x) > f'(0) =1 > 0$$

$f'(x)>0$が示せたので、$f(x)$も単調増加することがわかる。

よって、

$$f(x) = e^x - \frac{x^2}{2} > 0$$
$$e^x > \frac{x^2}{2}$$

$e^x > \frac{x^2}{2}$より$\frac{1}{e^x} < \frac{1}{\frac{x^2}{2}}$

よって、

$$0 ≦ \frac{x}{e^x} < \frac{x}{\frac{x^2}{2}} = \frac{2}{x}$$

$\frac{2}{x} \underset{x\to \infty}{\longrightarrow} 0$より、はさみうちの原理から

$$\lim_{x\to \infty}\frac{x}{e^x}=0\ \cdots ①$$

が示せた。

小春

なるほど、わざわざ$\frac{2}{x}$で挟み込むために繁分数を利用したかったのね。

①が示せたらあとは簡単です。

$$\lim_{x\to \infty}\frac{\log x}{x}$$

において$x=\log t$とおくと、

$x\to \infty$のとき$t\to\infty$
$x = e^t$

なので

$$\lim_{x\to \infty}\frac{\log x}{x} =\lim_{t\to \infty} \frac{t}{e^t} = 0$$

と①に帰着でき、

$$\lim_{x\to \infty}\frac{\log x}{x}=0\ \cdots ②$$

が示せました。

小春

これは確かに一回やらないと辛いね。。。

①、②の証明はよく（誘導付きで）入試問題にもなりますが、発散の速さを意識するとこれらの事実をパッと使えるので強いですね。

【まとめ】

楓

最後にまとめます！

まとめ

いろいろな関数が組み合わさった関数の極限を求めるためには、各関数の極限の発散・収束の速さに着目して解けば良い。

発散・収束の速さはグラフから考えることも有効ですが、一番手っ取り早いのは

の事実を使うことが一番効率的です。

どうでしょう、ちょっとはできそうな気がしてきましたか？

練習問題を下に載せておきましたので、是非慣れてくださいね〜。

以上、「いろんな関数の発散・収束の速さ」についてでした。

チェック問題

例題

$$\lim_{x\to +0} x^2\log x$$

$\log x$がノロノロと$-\infty$に向かうのに対して、指数関数$x^2$は急激に0に収束します。

よって$0\times 定数$と同じような状況になるため、

$$\lim_{x\to +0} x^2\log x = 0$$

となります。

例題

$$\lim_{x\to\infty} \frac{\left(e^x-1\right)\left(e^x+2x\right)}{x^2-e^{2x}}$$

分母・分子に$\frac{1}{e^{2x}}$をかけると、

\begin{align} \frac{\left(e^x-1\right)\left(e^x+2x\right)}{x^2-e^{2x}} &= \frac{\left(e^x-1\right)\left(e^x+2x\right)\cdot \color{red}{\frac{1}{e^{2x}}}}{\left(x^2-e^{2x}\right)\cdot \color{red}{\frac{1}{e^{2x}}}}\\\ &= \frac{\left(1-\frac{1}{\color{red}{e^x}}\right)\left(1+\frac{2x}{\color{red}{e^x}}\right)}{\frac{x^2}{e^{2x}}-1}\\\ \end{align}

（※見切れている場合はスクロール）

$\frac{x^2}{e^{2x}},\ \frac{2x}{e^x}$は共に分子がべき関数、分母が指数関数なので、$x\to\infty$においては$\frac{定数}{\infty}$と同じになります。

よって、

\begin{align} \lim_{x\to\infty} \frac{\left(e^x-1\right)\left(e^x+2x\right)}{x^2-e^{2x}} &= \frac{1 \cdot 1}{0-1}\\\ &= -1\\\ \end{align}