【数列の極限の大小関係】イメージでわかる、知っててアタリマエの公式

楓

今日は数列の極限の大小関係を見ていくよ。

前回は極限値の演算をやったから、来ると思ってたよ！

小春

楓

今回扱う内容は、厳密な証明よりもイメージを大事にしよう！

あぁ、証明が大学数学になっちゃうんだね・・・。

小春

数列の極限の大小関係

数列の極限の大小関係で押さえておくべき公式はこれ！

また、この公式から次のことも言えます。

それでは、詳しく見ていきましょう！

ポイントは『グラフをイメージすること』です。

\(a_n≦b_n(n=1,2,3,\cdots)\)ならば、\(\alpha≦\beta\)

具体的に考えてみましょう。

厳密な証明は大学で行うので、ここでは感覚的に捉えておけばOK。

そのためにグラフを用いて、大小関係を把握してみましょう。

\(a_n=-\frac{1}{n}\)を\(y=-\frac{1}{x}\)、\(b_n=\frac{1}{n}+1\)を\(y=\frac{1}{x}+1\)と読み替えてみます。

ただし、数列における\(n\)は自然数なので、この時の\(x\)は自然数の値しか取りません。

この条件のもと、グラフを描いてみるとこのようになります。

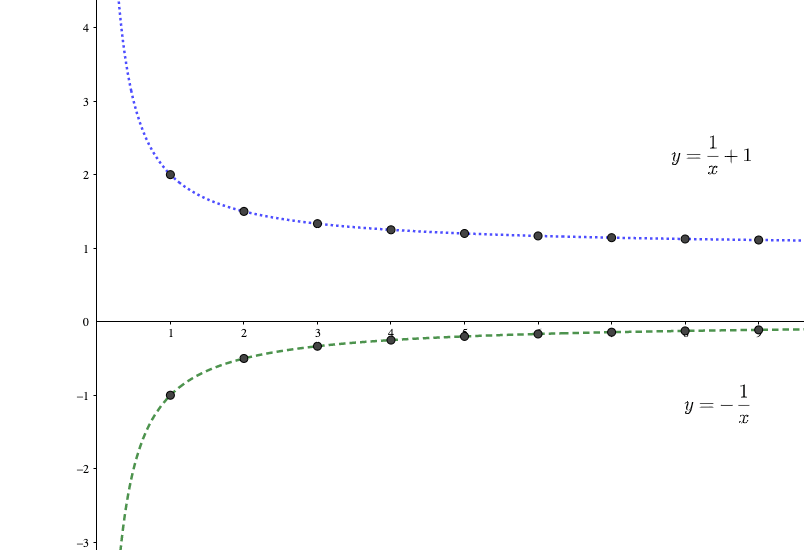
グラフを見てみると、\(n\)がどんな値をとっても\(a_n≦b_n\)が常に成り立つのであれば、\(a_n\)の極限値が\(b_n\)の極限値よりも小さいことが分かりますね。

この公式の凄いところは、直接極限値を求めなくても、数列の大小関係だけで極限値の大小関係がわかるところです。

\(a_n≦X(n=1,2,3,\cdots)\)ならば、\(\alpha≦X\)

先ほどの公式

の数列\(\{a_n\},\{b_n\}\)が

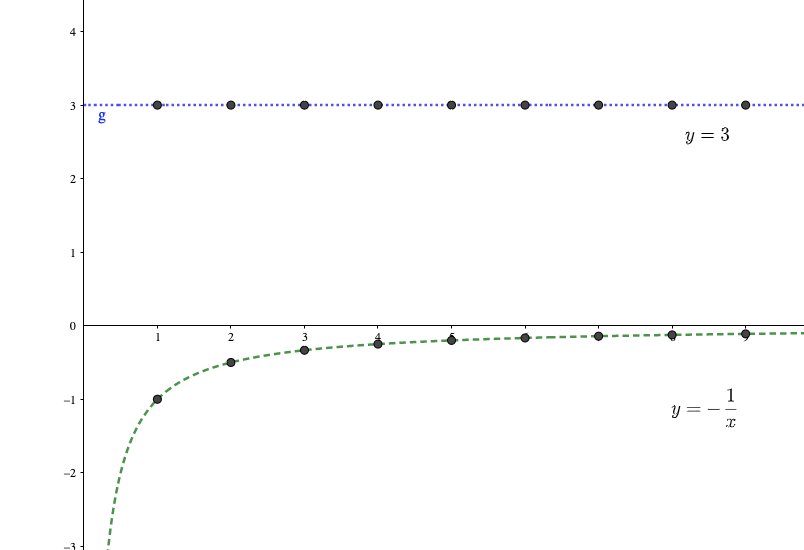
のような場合を考えてみます。

すると、グラフは見てわかる通り、数列\(\{a_n\}\)のどの項も3より小さいため、極限値も3を下回っていますね。

楓

だからと言って極限値が3とは限らないよ！

あくまで「\(\{a_n\}\)の極限値＜3」ということが言えただけなんだね。

小春

楓

それでも、極限値を求めなくても大小関係がわかることが後々大事になるよ。

\(Y≦b_n(n=1,2,3,\cdots)\)ならば、\(Y≦\beta\)

これも1つ目の公式をもとに考えれば、それほど難しくありません。

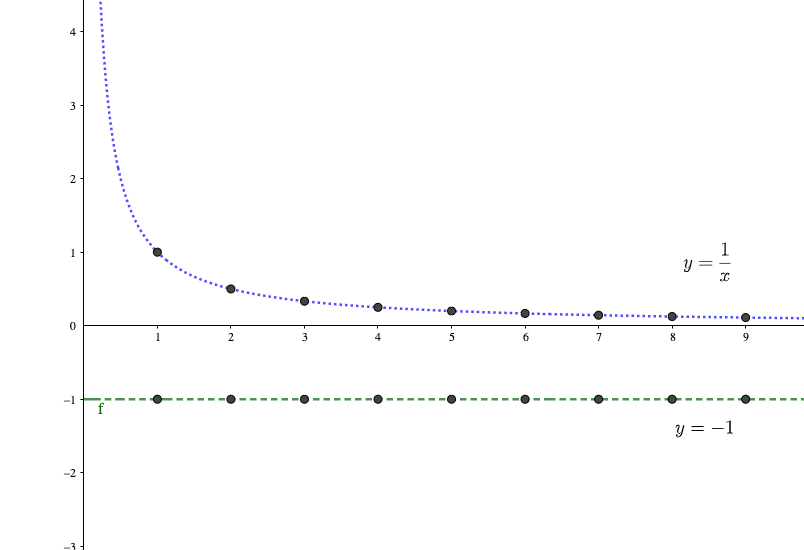
の数列\(\{a_n\},\{b_n\}\)が

のような場合を考えてみます。

すると、グラフは見てわかる通り、数列\(\{b_n\}\)のどの項も\(-1\)より大きいため、極限値も\(-1\)を上回っていますね。

数列の極限の大小関係の注意点

今回扱った公式には、いくつか勘違いしやすい点があります。

どの項でも大小関係が覆らない

まず、3つの公式の前提には

ということが挙げられています。

そのため、例えば

という場合には、これら3つの公式は使えません。

楓

あくまで\(n=1,2,3,\cdots\)のどの場合でも、\(a_n ≦ b_n\)が成り立たなければ意味がないんだ。

収束すること

そして3つの公式では、2つの数列が極限値\(\alpha,\beta\)を持っていることも前提に含まれています。

つまり、これは数列が収束することが仮定されているので、発散する場合にこれらの公式は使えないということになります。

楓

ただし発散する場合は、『追い出しの原理』というものが考えられるよ！

参考【追い出しの原理】不等式を作って、発散することを示せばOK。あんまり使われないけどね・・・。

まとめ

楓

最後にまとめるね。

今回得たこの大小関係の公式は、これから先かなり重要になる『はさみうちの原理』のもとになります。

そのため、まとめにも書きましたが、

『極限値が直接求まらなくても、大小関係は比較することができる。』

という点を、よく覚えておきましょう。

以上、「数列の極限の大小関係」についてでした。