【等比数列の極限】暗記は絶対にダメ！絶対必要な極限の感覚をマスターしよう。

Today's Topic

初項$a$、公比$r$の等比数列$\{ar^{n-1}\}$の極限には、

$r>1$のとき、$a_n \underset{n\to \infty}{\longrightarrow} \infty$
$r=1$のとき、$a_n \underset{n\to \infty}{\longrightarrow} a$
$0<r<1$のとき、$a_n \underset{n\to \infty}{\longrightarrow} 0$
$-1<r<0$のとき、$a_n \underset{n\to \infty}{\longrightarrow} 0$
$r<-1$のとき、$a_n \underset{n\to \infty}{\longrightarrow} 振動$

という性質がある。

ただし、これは覚えるのではなく、実際に調べた方がラク。

楓

今日は等比数列の極限について考えよう、と言っても暗記するものは何もないよ！

なんか学校だと4つくらい公式覚えさせられた気が・・・。

小春

楓

あぁ、あんなのいらないよ。内容的には小学生の算数レベルだから。

この記事を読むと、この問題が瞬間的にわかる！

$$\lim_{n\to\infty}\frac{2^n+1}{3^n}$$
$$\lim_{n\to\infty}\frac{2^n-(-5)^n}{(-5)^n+3^n}$$

楓

1つは具体例で、もう1つは最後に答え合わせするね！

Contents

1 かける数によって、どのように数が変わるのか
2 等比数列の極限の性質
3 等比数列の極限の例題
4 まとめ

かける数によって、どのように数が変わるのか

「等比数列の極限」とタイトルをつけていますが、結論から言ってしまえば、別に「等比数列だから特別なことがある」というわけではありません。

等比数列よりも、どちらかと言えば「掛け算」の性質に近いです。

じっくり具体例を見ながら考えていきましょう。

公比が1よりも大きい場合

例題

数列$\{a_n\}$の一般項が

$$a_n = 3\cdot 2^{n-1}$$

のとき、この数列の極限を求めよ。

初項が3、公比が2。

この数列はつまり、「3に2をどんどんかけていく」ということを表しています。

楓

$3\times2$は？

$6$でしょ？

小春

楓

$3\times2\times2$は？

$12$だよ・・・

小春

楓

$3\times2\times2\times\cdots$

いつまでやるの・・・泣

小春

楓

値はどんどん・・・？

あ、大きくなっていくね！

小春

このように、公比が1よりも大きい数列の場合、項が進むにつれて値は大きくなっていきます。

よって、

$$\lim_{n\to\infty}a_n = \infty$$

ということが分かりますね。

公比が0以上1以下の場合

例題

数列$\{a_n\}$の一般項が

$$a_n = 3\cdot \left(\frac{1}{2}\right)^{n-1}$$

のとき、この数列の極限を求めよ。

初項が3、公比が$\frac{1}{2}$。

この数列はつまり、「3に$\frac{1}{2}$をどんどんかけていく」ということを表しています。

ポイント

公比が分数のとき、小数に直して考えてみると考えやすくなる。

$\frac{1}{2}=0.5$と1よりも小さく、掛けるたび値は半分になっていきますね。

そのため、項が進むにつれて値はどんどん小さくなりますが、決して0にはなりません。

よって、

$$\lim_{n\to\infty}a_n = 0$$

ということが分かります。

小春

つまり0に収束する（0に近づき続ける）んだね！

公比が1の場合

例題

数列$\{a_n\}$の一般項が

$$a_n = 3\cdot 1^{n-1}$$

のとき、この数列の極限を求めよ。

楓

1は何回かけても・・・？

値は変わらない・・・？

小春

楓

だから・・・？

極限も変わらない・・・

小春

よって、

$$\lim_{n\to\infty}a_n = 3$$

ということが分かります。

公比が負の場合

公比が負の場合には、2パターン考えることができます。

どちらもギザギザな動きをすることが特徴的ですが、発散か・収束かが異なります。

絶対値が1よりも大きい

例題

数列$\{a_n\}$の一般項が

$$a_n = \left(-\frac{11}{10}\right)^{n-1}$$

のとき、この数列の極限を求めよ。

ポイント

公比が負のとき、$-1$を切り離して考えてみると考えやすくなる。

初項が1、公比が$(-1)^{n-1}\times\left(\frac{11}{10}\right)^{n-1}$。

一旦$-1$を除外して考えてみると、1に$\frac{11}{10}$をかけ続けると値は次第に大きくなっていきますね。

小春

$\frac{11}{10}$は1よりも大きいもんね。

ここで$-1$をかけ続けるとどうなるか考えてみると・・・。

小春

$-1$をかけるたびに、プラスマイナスが入れ替わるね。

グラフで捉えてみると、

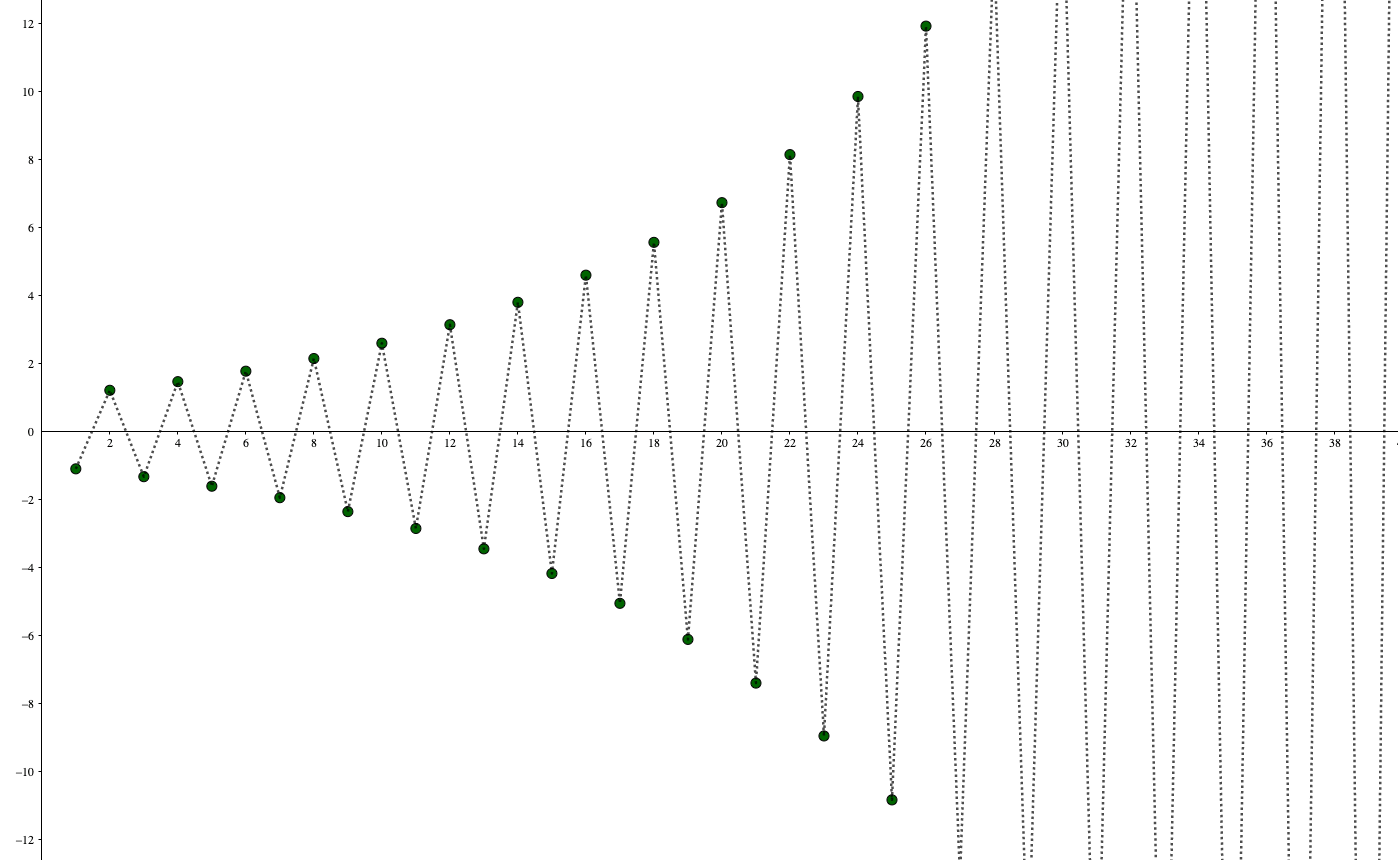
このように振動していることが分かります。

よって、

$$\lim_{n\to\infty}a_n = 振動$$

ということが分かります。

絶対値が1よりも小さい

例題

数列$\{a_n\}$の一般項が

$$a_n = 5\left(-\frac{12}{13}\right)^{n-1}$$

のとき、この数列の極限を求めよ。

先ほどと同様に、$-1$を切り離して考えてみましょう。

初項5に$\frac{12}{13}$をかけ続けると・・・

小春

$\frac{12}{13}<1$だから、どんどん値が小さくなる！

その通り！ただし、0にはならないからね。

楓

そして、$-1$をかけ続けるとどうなるか考えてみると・・・。

小春

やっぱり$-1$をかけるたびに、プラスマイナスが入れ替わるね。

グラフで捉えてみると、

小春

あ、しんどu・・・

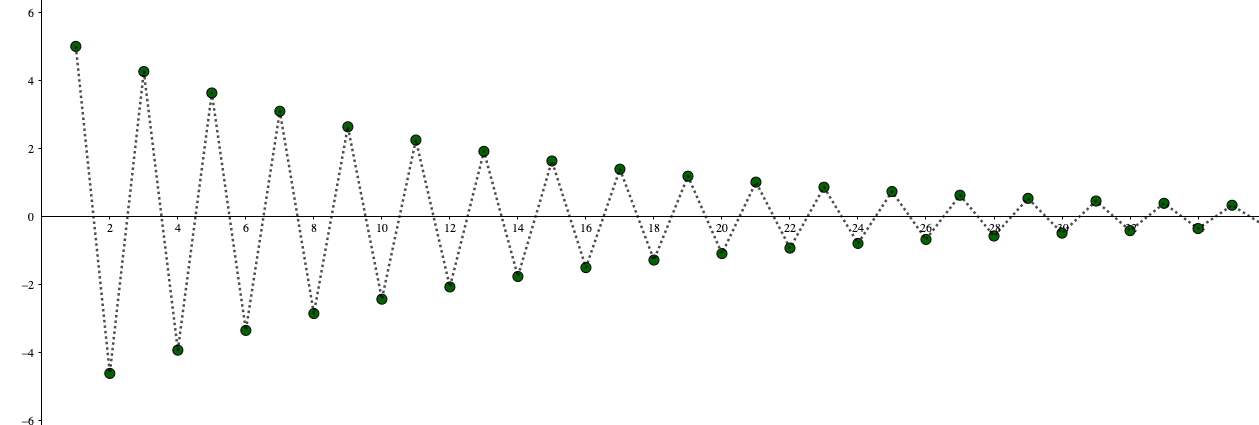
これは振動ではありません。

極限の基礎の記事でも紹介した通り、振動とはプラマイが入れ替わると同時に、発散する場合のことです。

今回はギザギザに動いてはいますが、値が小さくなり、最終的に0に収束しているため

$$\lim_{n\to\infty}a_n = 0$$

ということが分かります。

小春

・・・・・・

等比数列の極限の性質

以上のことをまとめると、

ポイント

初項$a$、公比$r$の数列$\{ar^{n-1}\}$の極限は、

$r>1$のとき、$a_n \underset{n\to \infty}{\longrightarrow} \infty$
$r=1$のとき、$a_n \underset{n\to \infty}{\longrightarrow} a$
$0<r<1$のとき、$a_n \underset{n\to \infty}{\longrightarrow} 0$
$-1<r<0$のとき、$a_n \underset{n\to \infty}{\longrightarrow} 0$
$r<-1$のとき、$a_n \underset{n\to \infty}{\longrightarrow} 振動$

となります。

楓

だけどこれを公式みたいに覚えるのは、なんというか労力の無駄だよね。。。

確かに、自分で「かけ続けるとどうなるかな」って考えた方が楽そうだね。

小春

等比数列の極限の例題

例題

$$\lim_{n\to\infty}\frac{2^n+1}{3^n}$$

そのまま考えると、$\frac{\infty}{\infty}$の不定形になってしまいますね。

そこで分母、分子を$2^n$で割って繁分数を考えてみると、

$$\frac{2^n+1}{3^n}=\frac{1+\left(\frac{1}{2}\right)^n}{\left(\frac{3}{2}\right)^n}$$

となります。

$\left(\frac{3}{2}\right)^n$は初項$\frac{3}{2}$に、$\frac{3}{2}$をかけ続けるわけですから値は次第に大きくなります。

$$ \left(\frac{3}{2}\right)^n \underset{n\to \infty}{\longrightarrow} \infty$$

一方、$\left(\frac{1}{2}\right)^n$は初項$\frac{1}{2}$に、$\frac{1}{2}$をかけ続けるわけですから値は次第に小さくなります。

$$ \left(\frac{1}{2}\right)^n \underset{n\to \infty}{\longrightarrow} 0$$

つまり、

\begin{align} \lim_{n\to\infty}\frac{2^n+1}{3^n} &= \lim_{n\to\infty}\frac{1+\left(\frac{1}{2}\right)^n}{\left(\frac{3}{2}\right)^n} \\\ &= \frac{1+0}{\infty}\\\ &= 0 \\\ \end{align}

となります。

楓

$\frac{1}{\infty}$は分母がむちゃくちゃ大きい数ってことね。

分母が大きくなるほど0に近くなるけど、0にはならないね。

小春

メモ

今回は分母、分子を$2^n$で割りましたが、$3^n$で割っても結果は同じです。

$$\frac{2^n+1}{3^n}=\left(\frac{2}{3}\right)^n+\left(\frac{1}{3}\right)^n$$

なので、

\begin{align} \lim_{n\to\infty}\frac{2^n+1}{3^n} &= \lim_{n\to\infty} \left(\left(\frac{2}{3}\right)^n+\left(\frac{1}{3}\right)^n\right) \\\ &= 0\\\ \end{align}

まとめ

今日のまとめをするよ！

まとめ

初項$a$、公比$r$の等比数列$\{ar^{n-1}\}$の極限には、

$r>1$のとき、$a_n \underset{n\to \infty}{\longrightarrow} \infty$
$r=1$のとき、$a_n \underset{n\to \infty}{\longrightarrow} a$
$0<r<1$のとき、$a_n \underset{n\to \infty}{\longrightarrow} 0$
$-1<r<0$のとき、$a_n \underset{n\to \infty}{\longrightarrow} 0$
$r<-1$のとき、$a_n \underset{n\to \infty}{\longrightarrow} 振動$

という性質がある。

ただし、これは覚えるのではなく、実際に調べた方がラク。

今回学んだことは、今後極限の計算をしていく上で重要な考え方になります。

公式として覚えずに、公比を見極めて『かけ続けるとどうなるか』を考えていきましょう。

以上、「等比数列の極限について」でした。

チェック問題

例題

$$\lim_{n\to\infty}\frac{2^n-(-5)^n}{(-5)^n+3^n}$$

$3^n$や$2^n$で割ると、振動する部分が出てくるため考えにくくなります。

$(-5)^n$で割ると、

\begin{align} \lim_{n\to\infty}\frac{2^n-(-5)^n}{(-5)^n+3^n} &= \lim_{n\to\infty}\frac{\left(-\frac{2}{5}\right)^n-1}{1+\left(-\frac{3}{5}\right)^n}\\\ &= \frac{0+0}{1}\\\ &=0\\\ \end{align}