【発散・収束・振動】無限数列から始める、極限の着目すべき点と考え方

Today's Topic

$$\lim_{n\to \infty} a_n = \alpha$$

楓

今日は理系数学の入門、そして最初の関門とも言える極限について考えるよ！

授業でやったときは「代入すればいいのかな？」って感じだったよ？

小春

楓

実は代入っぽく見えて、壮大なことを考えているんだ。まずは言葉の定義や考え方から！

この記事を読むと、この問題がわかる！

$$\sqrt{\frac{5}{3}},\sqrt{\frac{11}{6}},\sqrt{\frac{17}{9}},\sqrt{\frac{23}{12}},\cdots$$で表される無限数列の極限を求めよ。
$$3,3,3,3,3,\cdots$$で表される無限数列の極限を調べよ。

楓

答えは最後に扱うよ！

Contents

1 無限数列と極限
2 極限を考えるときのコツ
3 数列の発散
4 まとめ

無限数列と極限

これまで考えてきた数列は、第$n$項までの有限個の項のみを考えてきました。

このような数列を有限数列といい、ここから先は無限個の項が続く無限数列を考えます。

楓

数Ⅲ以降では、一般に無限数列のことを数列というよ！

例として、数列$a_n=\frac{1}{n}$を見てみましょう。

$n$を大きくしていくにつれて、次第に項が0に近づいていきますよね？

$$1, \frac{1}{2},\frac{1}{3},\frac{1}{4},\cdots$$

楓

だんだん値が小さくなっていくのがわかるね。

値は小さくなるけど、負の値にはならないから、最終的に0になりそうね。

小春

このように、$n$を大きくしていくにつれて、項がある数$\alpha$に近づくとき、この数を極限値といい、

$$\lim_{n\to \infty} a_n = \alpha$$
$$a_n \underset{n\to \infty}{\longrightarrow} \alpha$$

のように書きます。

また極限値が存在する場合、その数列は「収束する」といいます。

極限を考えるときのコツ

極限値は、「 $n\to\infty$のとき、$\left\{a_n\right\}$が近づく値」のこと。

そんな極限値は、どのように見つければ良いのでしょうか。

結論から言えば、グラフを想像すると良いです。

例題

数列$a_n = \frac{10}{n}+1$の極限値を求めよ。

$y=\frac{10}{x}+1$と考えると、グラフは以下のようになります。

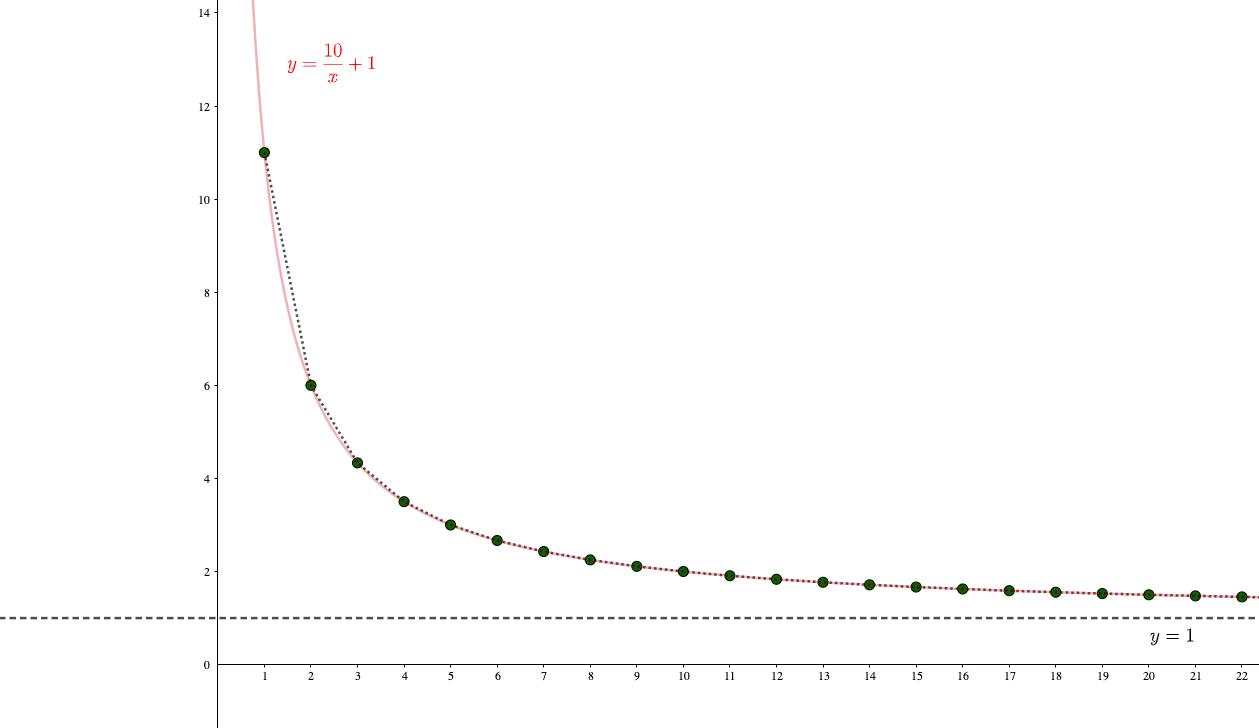
この図から、$x\to\infty$のとき$y$の値は次第に$y=1$に近づくことがわかりますね。

よって、

$$\lim_{n\to\infty} a_n = 1$$

小春

$a_n$を$y$に、$n$を$x$に読み替えればいいのね！

数列の発散

お察しの通り、収束する数列があれば、そうでない数列もあるということです。

収束しない数列は「発散する」と言われ、次の2通りが考えられます。

正・負の無限大に発散

例題

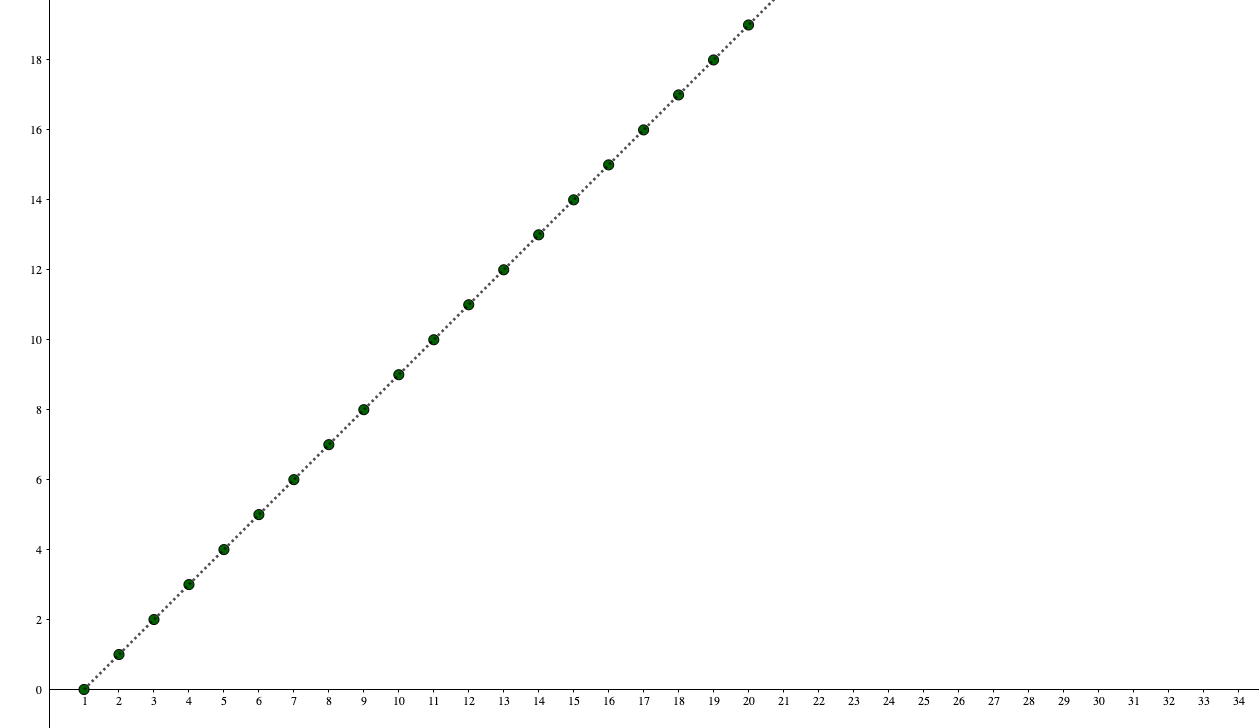
数列$a_n = n-1$の極限を調べよ。

$n$を大きくすればするほど項は大きくなり、ある値に近づく、なんてことはないですね。

小春

ずーっと値が大きくなっていくよね？

このようにずーっと大きくなり続けることを、

$$\lim_{n\to \infty}a_n = \infty$$

と表し、「正の無限大に発散する」といいます。

例題

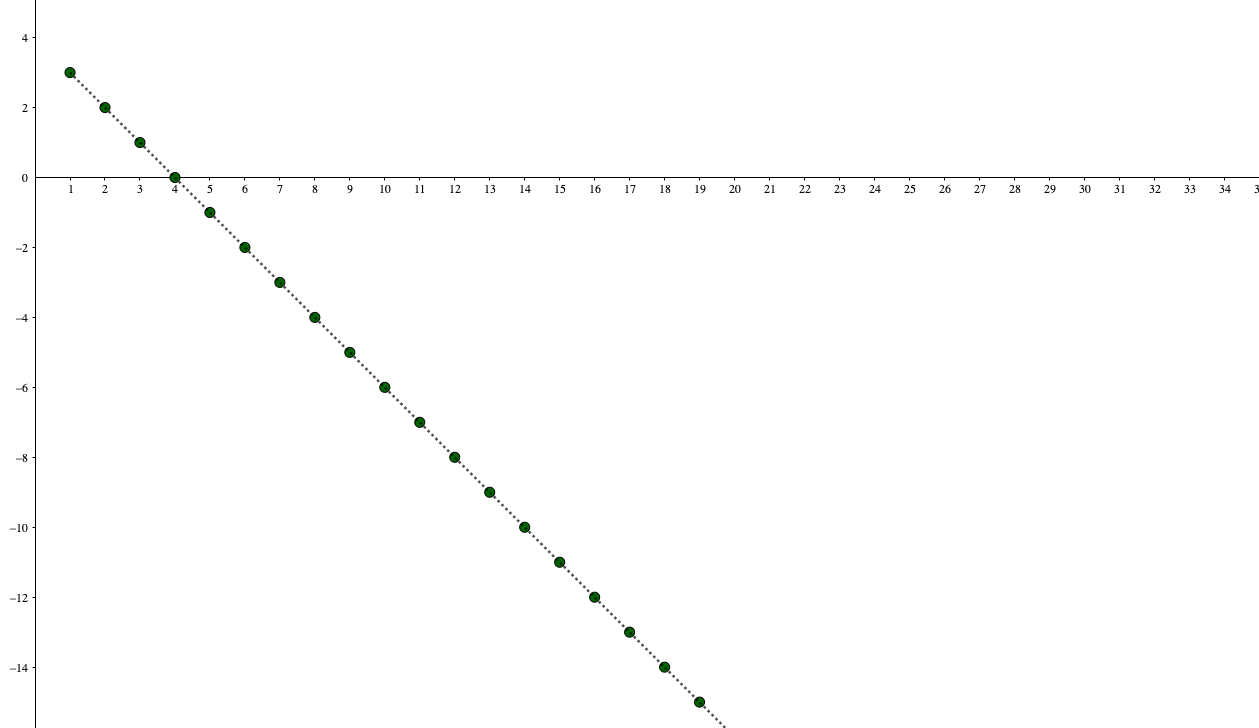
数列$a_n = -n+4$の極限を調べよ。

対して、この数列は$n$を大きくすればするほど項はマイナスに大きくなり続けますね。これを

$$\lim_{n\to \infty}a_n = -\infty$$

と表し、「負の無限大に発散する」といいます。

振動

例題

数列$a_n = (-1)^n n$の極限を調べよ。

この数列について考えてみると、

$$-1, 2, -3, 4, \cdots$$

のようにプラスマイナスを行き来し、一概に正の無限大にも、負の無限大にも発散していないようなものもあります。

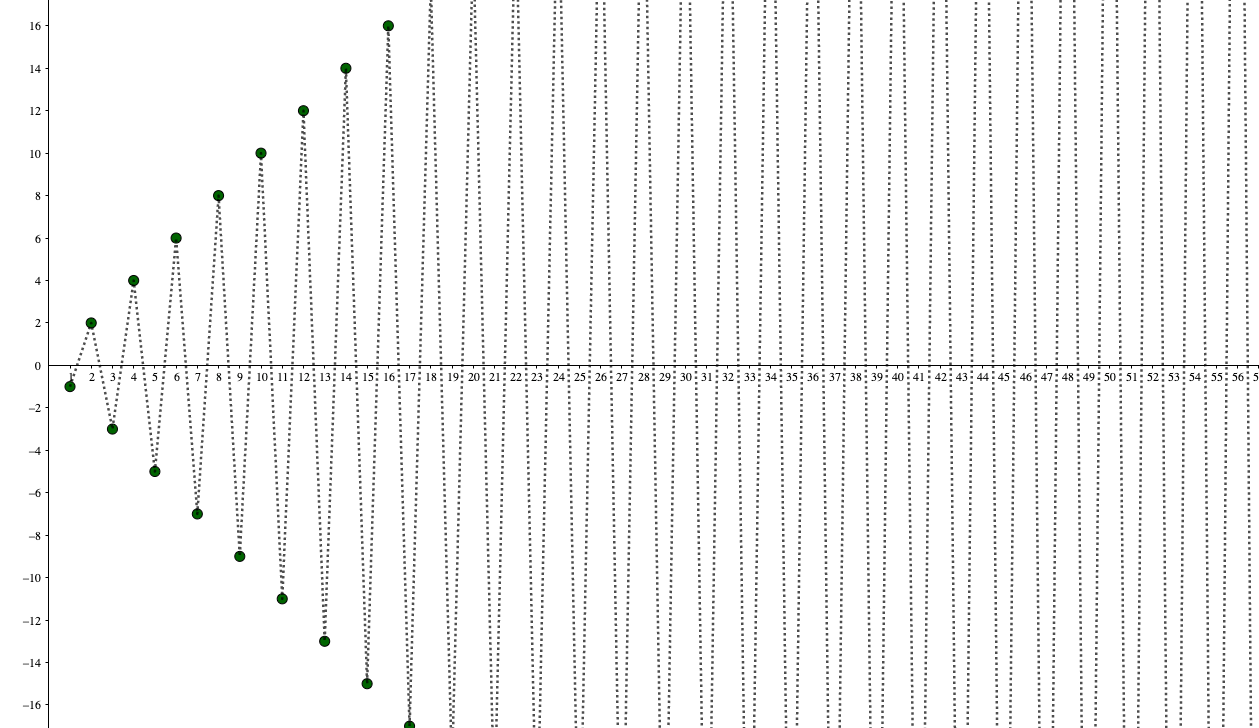
このような数列を「振動する」といい、個人的には一番好きくない数列の振る舞いです。

楓

振動するって扱いにくいから、出てきたら終わった感がある...

グラフを見れば、振動っていう意味がわかるね

小春

ただし、振動に似た形として注意しないといけないものがあります。

例題

数列$\left(-\frac{11}{12}\right)^n$の極限を調べよ。

こちらの数列も、$n$を大きくしていくとプラスマイナスが入れ替わって、振動しているように思えます。

しかし、ずっと$n$を大きくしていくと次第に収束していくことがわかります。

このような場合、この数列は収束しているので振動しているとは言えません。。。

楓

振動はあくまで「発散」の一部ね。

グラフが想像できないとき

しかし数列はいろんなバラエティを考えることができるので、グラフが想像できないときもあります。

そんなときは極限の公式を駆使して、解決していきます。

例題

数列$a_n = \frac{3+n^2}{n}$のとき、極限値があるか調べよ。

$$\frac{3+n^2}{n} = 3\times\frac{1}{n} + n$$

さらに、

$$\frac{1}{n} \underset{n\to \infty}{\longrightarrow} 0$$
$$ n \underset{n\to \infty}{\longrightarrow} \infty$$

より、

\begin{align} \lim_{n\to\infty} a_n &= \underbrace{3\times 0 + \infty}_{ここは解答に書かない} \\\ &= \infty\\\ \end{align}

よって、極限値はなく、正の無限大に発散する。

小春

途中式は書いちゃいけないの？

$\infty$は「無限に大きくなる」という概念であって数ではないから、計算はできないんだ。

楓

小春

なるほど、あくまで自分の中で理解できるようにメモ書き程度にしておこうってことね！

極限の計算法則については、「【数列の極限の性質】数列の問題は、結局この4つの公式に持っていければOK」を参考にしてください。

: 【極限の性質】リミットには分配法則が成り立つが、特殊な解釈をしているゾ！

続きを見る

まとめ

楓

今日のまとめ！

まとめ

数列$\left\{a_n\right\}$が$n\to\infty$のとき、ある値$\alpha$に近づくとき、$\alpha$を極限値といい、数列は収束するという。

収束しない数列は発散する。

数列が収束するかどうか調べるためには、

グラフをもとに考える
極限公式をもとに考える

のどちらかを用いれば良い。

ここから先は極限公式を求める旅に出発します。

どんな数列でもグラフがわかるわけではないので、ある程度式だけで解決できるようになっておいたほうが確実ですからね。

ただ、この極限の分野は数学らしからぬ「感覚」を重視して理解しましょう。

厳密な証明は大学数学で行われるので、まずは勘が働くように努力したほうが良いですよ。

以上、「無限数列と極限について」でした。

チェック問題

例題

$$\sqrt{\frac{5}{3}},\sqrt{\frac{11}{6}},\sqrt{\frac{17}{9}},\sqrt{\frac{23}{12}},\cdots$$で表される無限数列の極限を求めよ。

この数列の一般項は$a_n = \sqrt{\frac{6n-1}{3n}}$と表せる。

よって、$\frac{1}{n} \underset{n\to \infty}{\longrightarrow} 0$に注意すると、

\begin{align} a_n &= \sqrt{\frac{6n-1}{3n}}\\\ &= \sqrt{2-\frac{1}{3n}}\\\ &\underset{n\to \infty}{\longrightarrow} \sqrt{2-0} \\\ &= 2 \end{align}

小春

ほぼ直線じゃん！

例題

$$3,3,3,3,3,\cdots$$で表される無限数列の極限を調べよ。

この数列の一般項は、$a_n = 3$

よって、

$$a_n \underset{n\to \infty}{\longrightarrow} 3$$

より、この数列は3に収束する。

【発散・収束・振動】無限数列から始める、極限の着目すべき点と考え方

無限数列と極限

極限を考えるときのコツ

数列の発散

正・負の無限大に発散

振動

グラフが想像できないとき

【極限の性質】リミットには分配法則が成り立つが、特殊な解釈をしているゾ！

まとめ

【微分公式一覧】証明や差がつくポイント、役立つテクニックなど総まとめ

【感覚で理解できる！】常用対数とは？意味と使い方を徹底解説！！

自然対数、ネイピア数とは？なぜあの定義なのか、何が自然なのか。お金の話で超簡単に理解できる！！

【指数関数の定義】なぜ底が負のときは定義しないのか→ダルいから

【整数の指数法則】なぜ0乗が1なのか、息をするようにわかる指数法則