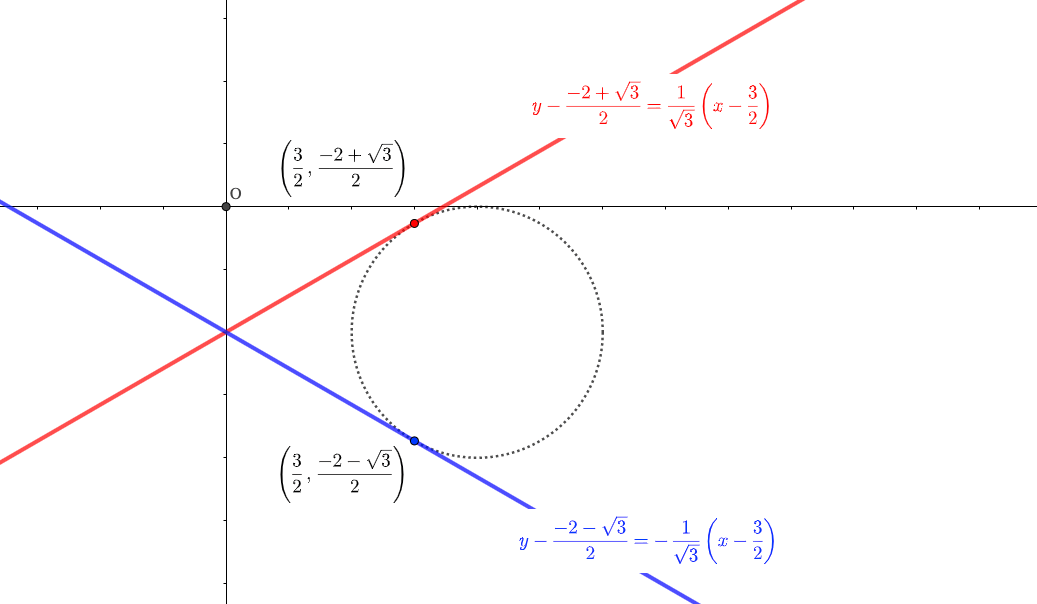【陰関数の接線】あえて陰関数に持ち込んで、複雑な接線を求めるテクニック

Today's Topic

陰関数の接線は、

陰関数の微分法を用いて傾きを求め、
平行移動をすれば良い。

複雑な方程式を持つ図形の接線を求めるためには、陰関数の微分法に帰着させた方が良い、マジで

楓

今日はいよいよ陰関数の最後、接線の方程式を求めてみよう！

結局陰関数を使う場面てパッとしないイメージだなぁ。

小春

楓

だよね、ところが今日は陰関数にあえて持ち込むことで問題を簡単にするコツを教えるよ！

あえて？！複雑にならないのかな？

小春

この記事を読むと、この問題が簡単にわかる！

円$(x-2)^2+(y+1)^2=1$において$x=\frac{3}{2}$のときの接線を求めよ。

楓

これを陰関数にすることで秒殺するよ！

Contents

1 陰関数の接線　基本例題
2 陰関数にあえて持ち込むテクニック
- 2.1 【めんどくさっ】凡人のする解法
3 まとめ

陰関数の接線　基本例題

楓

それではまず、基本的な問題から見ていきましょう。

結論から言うと、陰関数だからと言って接線の求め方はこれまで通り、

「微分して→傾き求めて→平行移動」

です。

例題

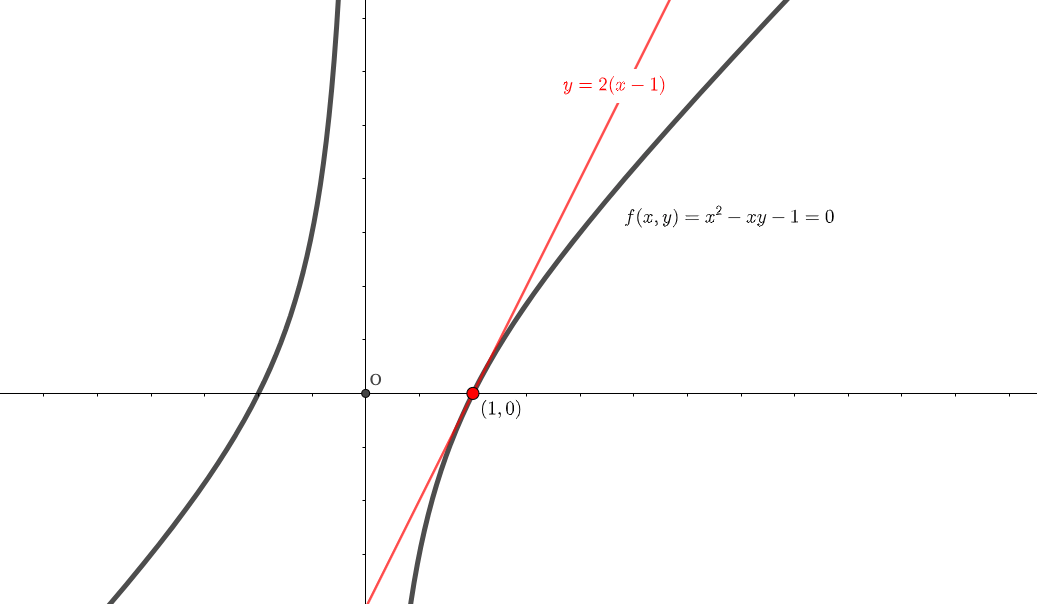
陰関数$f(x,y) = x^2-xy-1=0$の点$\left(1,0\right)$における接線の方程式を求めよ。

STEP1 微分する

陰関数の微分法より、両辺$x$について微分すると

\begin{align} f’(x,y) &= \frac{d}{dx} x^2 -\frac{d}{dx}(xy) \\\ &= 2x - \underbrace{\left(\frac{d}{dx}x\cdot y + x\cdot\frac{d}{dx}y\right)}_{積の微分法}\\\ \end{align}

より、

$$\frac{dy}{dx} = \frac{2x-y}{x}$$

STEP2 傾きを求める

よって、$\left(1,0\right)$における接線の傾きは

$$\frac{2\times 1 - 0}{1} =2$$

STEP3 平行移動する

$\left(1,0\right)$を通るように$y=2x$を平行移動させて、

$$y = 2(x-1)$$

陰関数にあえて持ち込むテクニック

陰関数そのものが問題として出題されるよりも、解法として陰関数を利用したほうが便利なことの方が多いです。

そこで、「陰関数にあえて持ち込むというテクニック」をご紹介しますね。

例題

楕円$\frac{1}{3}x^2 + \frac{1}{4}y^2 = 1$の点$\left(1, -\frac{2}{3}\sqrt{6}\right)$における接線の方程式を求めよ。

陰関数$f(x,y) = \frac{1}{3}x^2 + \frac{1}{4}y^2 -1 = 0$について考える。

この陰関数を両辺$x$について微分すると、

\begin{align} f’(x,y) &= \frac{2}{3} x + \frac{1}{4}\cdot \underbrace{\frac{d}{dy}y^2\cdot \frac{dy}{dx}}_{合成関数の微分公式} \\\ &= 0\\\ \end{align}

よって、

$$\frac{dy}{dx} = -\frac{4x}{3y}$$

点$\left(1, -\frac{2}{3}\sqrt{6}\right)$における接線の傾きは、次のようになる。

$$-\frac{4\times 1}{3\times \frac{2}{3}\sqrt{6}} = \frac{\sqrt{6}}{3}$$

以上より、接線の方程式は点$\left(1, -\frac{2}{3}\sqrt{6}\right)$を通るように$y=\frac{\sqrt{6}}{3}x$を平行移動すれば良いので、

$$y + \frac{2}{3}\sqrt{6} = \frac{\sqrt{6}}{3} (x-1)$$

小春

あれ、楕円て関数じゃないけど陰関数としていいの？

思い出して！陰関数は関数じゃなくてもOKだったね！

楓

小春

あ、あぁ〜。。。そ、そうだったね。。。

参考陰関数って何？って質問に全力で答えてみた【関数だけど関数じゃない】

絶対忘れてるじゃん！じゃあ、陰関数を使わない解法パターンを見てみて！メリットを痛感するから！

楓

【めんどくさっ】凡人のする解法

楕円の方程式を関数で表すと、 $\frac{1}{4}y^2 = 1-\frac{1}{3}x^2$より、

$$y = \pm 2\sqrt{1-\frac{1}{3}x^2}$$

接点は第4象限に属するため、$0<x, y<0$の時を考えれば良い。

よって、

$$y = - 2\sqrt{1-\frac{1}{3}x^2}$$

このとき、

\begin{align} y’ &= \left\{-2\left(1-\frac{1}{3}x^2\right)^{\frac{1}{2}}\right\}' \\\ &= \underbrace{-2\times \frac{1}{2} \left(1-\frac{1}{3}x^2\right)^{-\frac{1}{2}}\cdot \left(-\frac{2}{3}x\right)}_{合成関数の微分公式}\\\ &= \frac{2}{3}x\left(1-\frac{1}{3}^2\right)^{-\frac{1}{2}} \end{align}

よって、点$\left(1, -\frac{2}{3}\sqrt{6}\right)$における接線の傾きは、

$$\frac{2}{3}\cdot \left(1-\frac{1}{3}\right)^{-\frac{1}{2}} = \frac{\sqrt{6}}{3}$$

以上より、接線の方程式は点$\left(1, -\frac{2}{3}\sqrt{6}\right)$を通るように$y=\frac{\sqrt{6}}{3}x$を平行移動すれば良いので、

$$y + \frac{2}{3}\sqrt{6} = \frac{\sqrt{6}}{3} (x-1)$$

楓

ね？めんどいでしょ・・・

関数を求めるところから始めないといけないし、ルートがあるせいで微分もめんどくさいね泣

小春

まとめ

楓

今日のまとめ！

まとめ

陰関数の接線は、

陰関数の微分法を用いて傾きを求め、
平行移動をすれば良い。

複雑な方程式を持つ図形の接線を求めるためには、陰関数の微分法に帰着させた方が良い、マジで

限られた試験時間の中で、微分に時間をかけることは正直愚かです。

微分はあくまで接線の傾きや増減表などに使うための道具であり、「微分しておしまい！」となるほど難しいものではありません。

ぜひ効率的に導関数や微分係数を求められるようになりましょう！

以上、「陰関数の接線の求め方」についてでした。

チェック問題

例題

円$(x-2)^2+(y+1)^2=1$において$x=\frac{3}{2}$のときの接線を求めよ。

はい、3STEPやりますよ。いつも通りですね。眠いですね。

陰関数$f(x,y) = (x-2)^2+(y+1)^2-1 =0$について考える。

step
1導関数を求める

両辺$x$について微分すると、

\begin{align} \frac{d}{dx}f(x,y) &= \frac{d}{dx}(x-2)^2 + \frac{d}{dx}(y+1)^2\\\ &= 2(x-2) + \frac{d}{dy}(y+1)^2 \cdot \frac{dy}{dx}\\\ &=2(x-2) +2(y+1)\cdot \frac{dy}{dx}\\\ &=0 \end{align}

（※見切れている場合はスクロール）

より$\frac{dy}{dx}=-\frac{x-2}{y+1}$

step
2微分係数を求める

与式より$x=\frac{3}{2}$のとき、$y=\frac{-2\pm\sqrt{3}}{2}$

よって微分係数は、

$x=\frac{3}{2},\ y=\frac{-2 + \sqrt{3}}{2}$のとき、$$-\frac{\frac{3}{2}-2}{\frac{-2+\sqrt{3}}{2}+1} = \frac{1}{\sqrt{3}}$$
$x=\frac{3}{2},\ y=\frac{-2 - \sqrt{3}}{2}$のとき、$$-\frac{\frac{3}{2}-2}{\frac{-2-\sqrt{3}}{2}+1} =- \frac{1}{\sqrt{3}}$$

step
3平行移動

以上より、

$y=\frac{1}{\sqrt{3}}x$を$\left(\frac{3}{2}, \frac{-2 + \sqrt{3}}{2}\right)$を通るように平行移動した直線と、

$y=-\frac{1}{\sqrt{3}}x$を$\left(\frac{3}{2}, \frac{-2 - \sqrt{3}}{2}\right)$を通るように平行移動した直線が接線となる。

よって、求める接線の方程式は

$$y - \frac{-2\pm \sqrt{3}}{2}=\pm \frac{1}{\sqrt{3}} \left(x-\frac{3}{2}\right)$$

【陰関数の接線】あえて陰関数に持ち込んで、複雑な接線を求めるテクニック