【漸近線】を調べ忘れる君へ漸近線に必要な知識を徹底的にまとめてみました。

Today's Topic

漸近線を調べるためには、

$$\lim_{x\to\infty}\left\{\frac{f(x)}{x}\right\} $$の極限の有無を調べてから、
$$b=\lim_{x\to \infty} \left(f(x)-ax\right)$$の有無を調べれば良い。

また、不連続な点での極限を調べれば良い。

小春

楓く〜ん、またグラフ描くときに漸近線調べ忘れたぁ泣

あぁ、よくわかる！僕も理転したての頃はそうだったよ。

楓

小春

漸近線ってそもそもどうやって調べればいいかも怪しいし、「あ、こいつ漸近線持ってるな！」ってどうやって判断すればいいの？

むむっ、実は漸近線を持っているかどうかの判断は、正しい挑み方ではないんだ・・・

楓

この記事を読むと、この意味がわかる！

漸近線の求め方
漸近線を調べるタイミング

楓

最後に練習問題をつけてみたよ！

Contents

1 漸近線とは
2 漸近線を持つ代表的な関数
3 漸近線の求め方
- 3.1 $y$軸に平行な漸近線の求め方
- 3.2 $y$軸に平行でない漸近線の求め方2STEP
  - 3.2.1 STEP1　$\frac{f(x)}{x}$の極限を調べる→傾きチェック
  - 3.2.2 STEP2　代入する
4 漸近線の有無の判別方法
5 まとめ

漸近線とは

小学校6年生で習う反比例のグラフを思い出してみましょう。

このグラフは$x$軸、$y$軸にむちゃくちゃ近くなりますが、絶対に交わることはありませんでしたね。

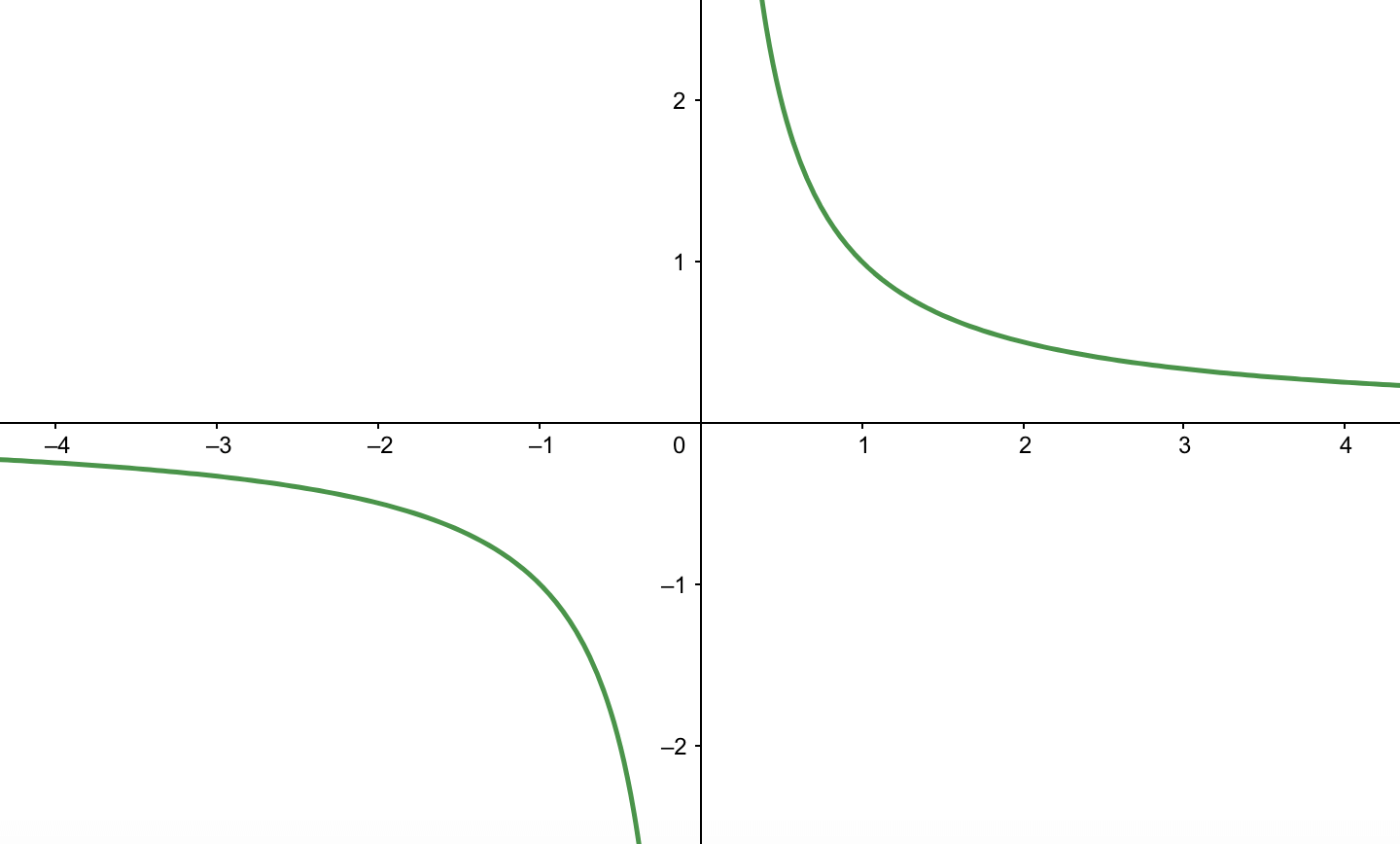
このとき、$x$軸、$y$軸のことを漸近線ぜんきんせんと言います。

つまり漸近線の定義を、ものすごくわかりやすく現実的にいうとこんな感じ。

定義

曲線Cがある直線$l$にギリギリ近づくも、どこまでいっても接したり、交わったりすることがないとき、この直線$l$のことを漸近線という。

漸近線を持つ代表的な関数

漸近線はない場合もありますし、複数ある場合もあります。

ですが漸近線を必ず持つとわかっている関数がいくつかあるので、最低限これらの関数は押さえておきましょう。

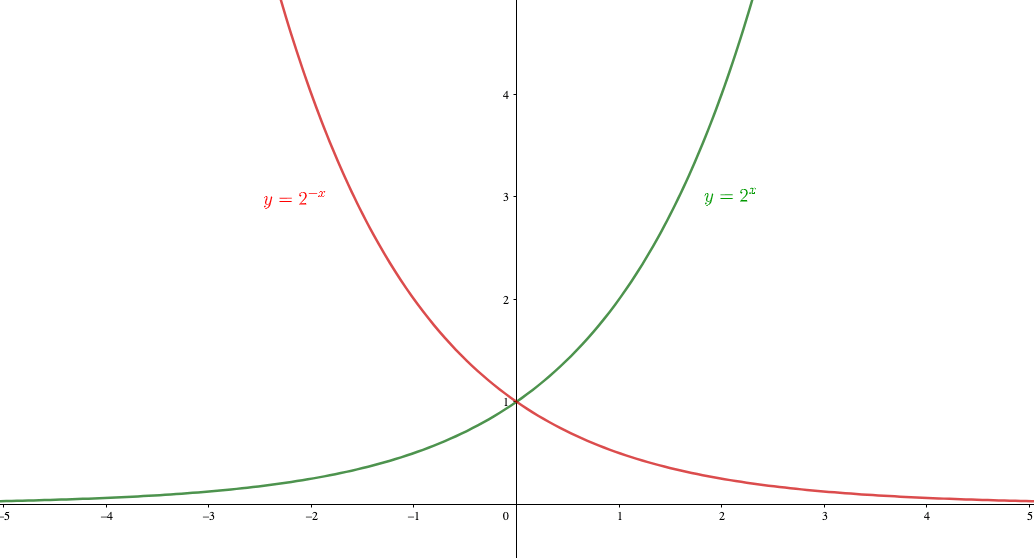
指数関数

$y=2^x,y=2^{-x}$はグラフのようになりますが、$x$軸に着目すると漸近線であることがわかります。

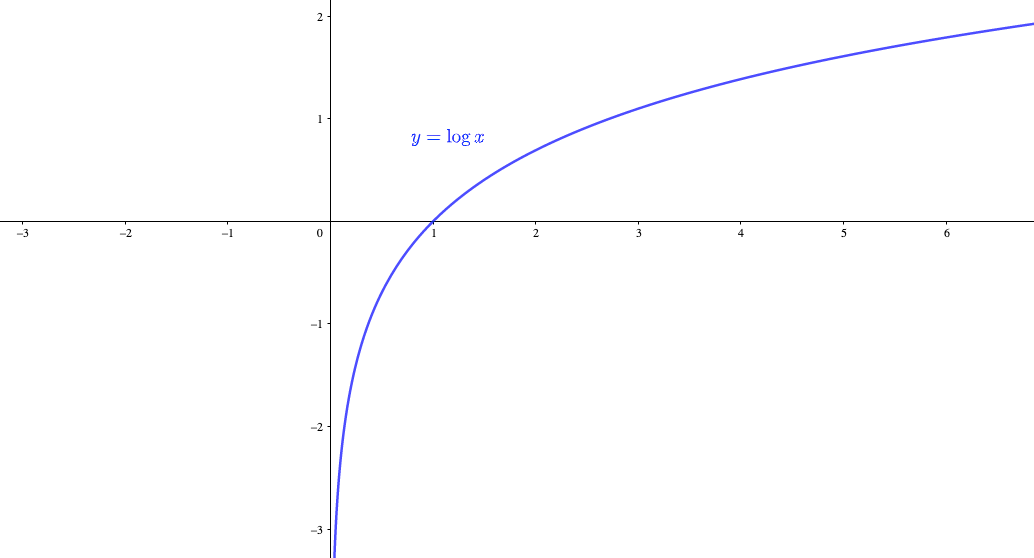
対数関数

$y=\log x$はグラフのようになりますが、$y$軸に着目すると漸近線であることがわかります。

タンジェント

$y=\tan x$はグラフのようになりますが、$x=\frac{\pi}{2}+n\pi\ (nは整数)$に着目すると漸近線であることがわかります。

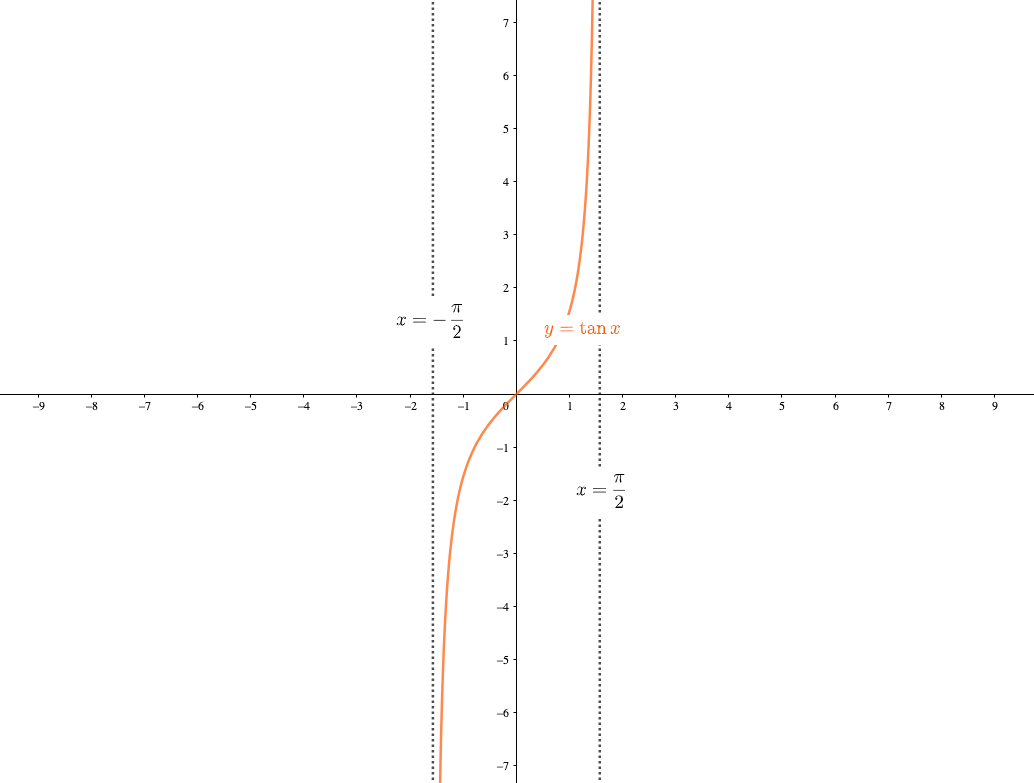
分数関数

例に見たような$y=\frac{1}{x}$だけでなく、$\frac{1}{x^2+1}$のような分数関数も、$x$軸に着目すると漸近線であることがわかります。

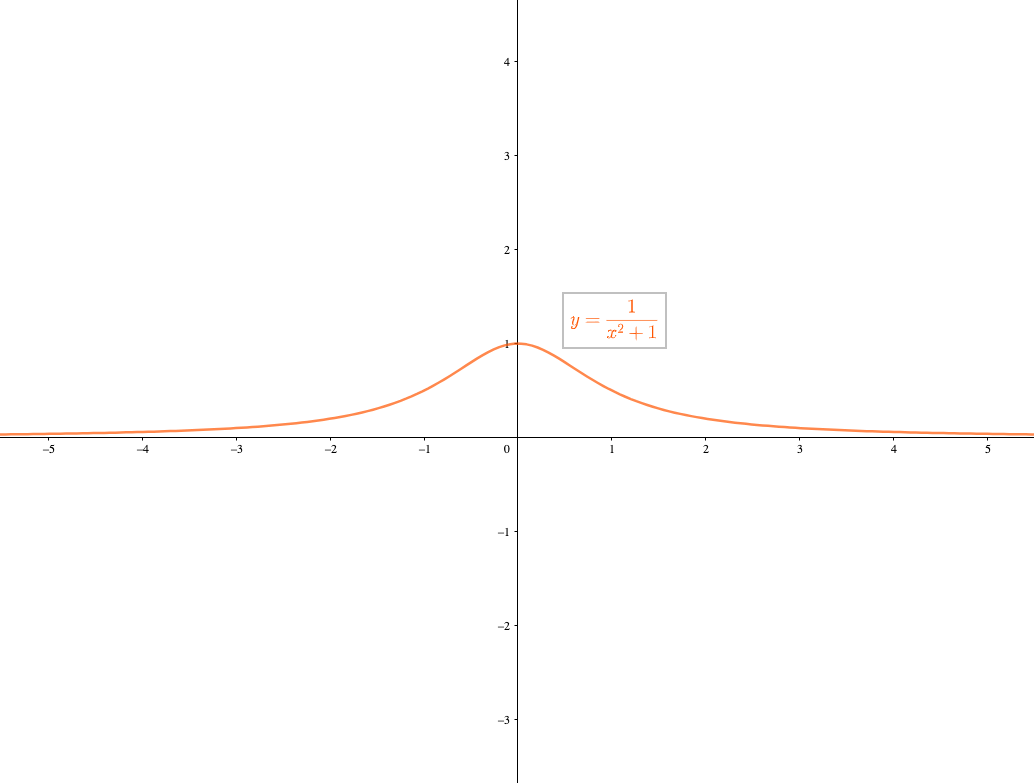
無理関数を含む関数

$y=\sqrt{x}$は漸近線を持ちませんが、$y=k\sqrt{x^2\pm a}+bx+c$の形で表されるような関数は漸近線を持ちます。

漸近線の求め方

漸近線は大きく分けて、２タイプに別れます。

$y$軸に平行な漸近線
$y$軸に平行でない漸近線

それぞれ求め方が異なるので、順に見ていきます。

$y$軸に平行な漸近線の求め方

ある関数$f(x)$が$y$軸に平行な直線$x=a$を漸近線に持つとき、以下極限のどれかを満たします。

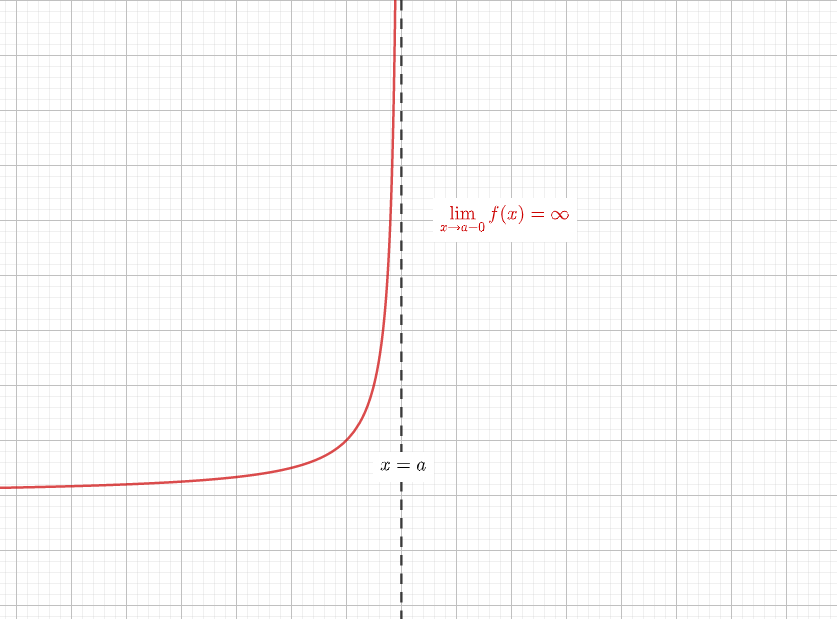
$$\lim_{x\to a-0}f(x) = \infty$$

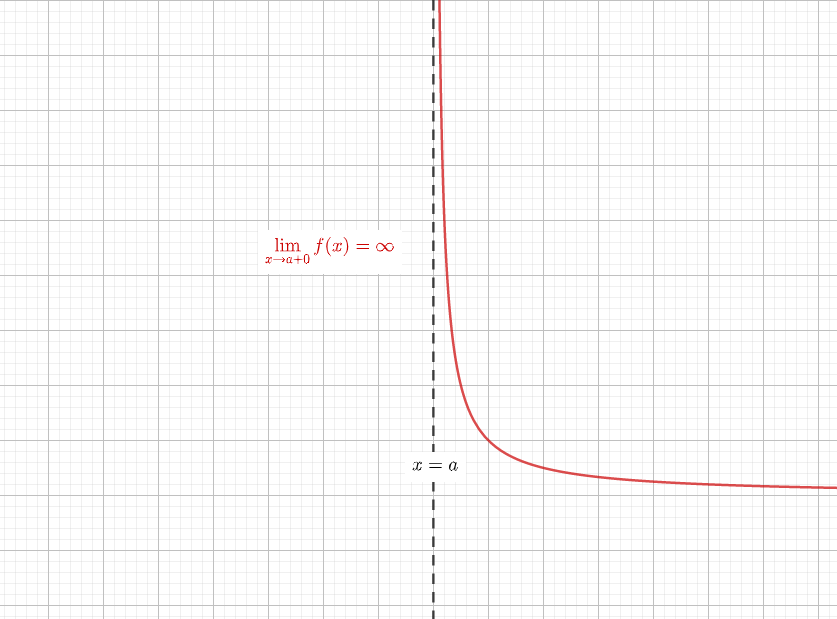
$$\lim_{x\to a+0}f(x) = \infty$$

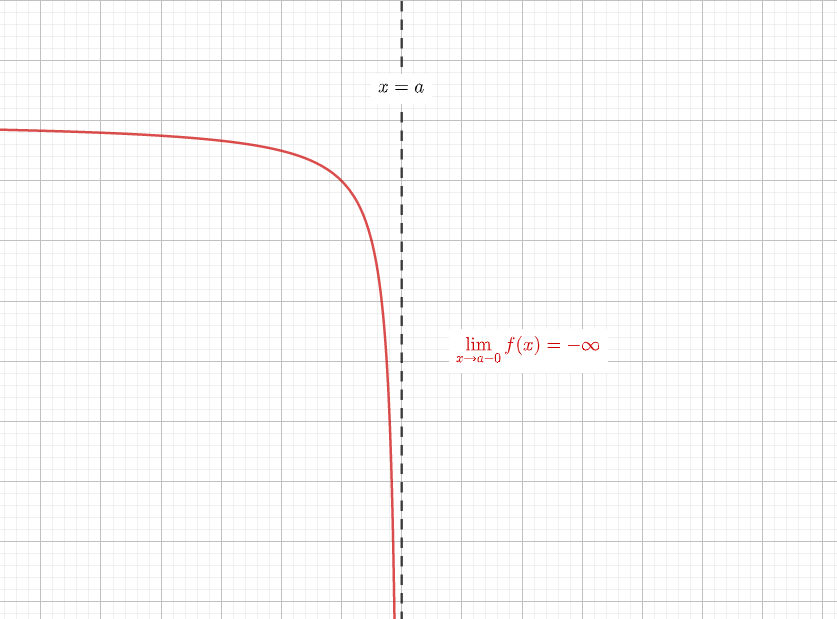
$$\lim_{x\to a-0}f(x) = -\infty$$

$$\lim_{x\to a+0}f(x) = -\infty$$

小春

つまり、このうちどれかでも満たせば、$y$軸に平行な直線を漸近線があるってことね！

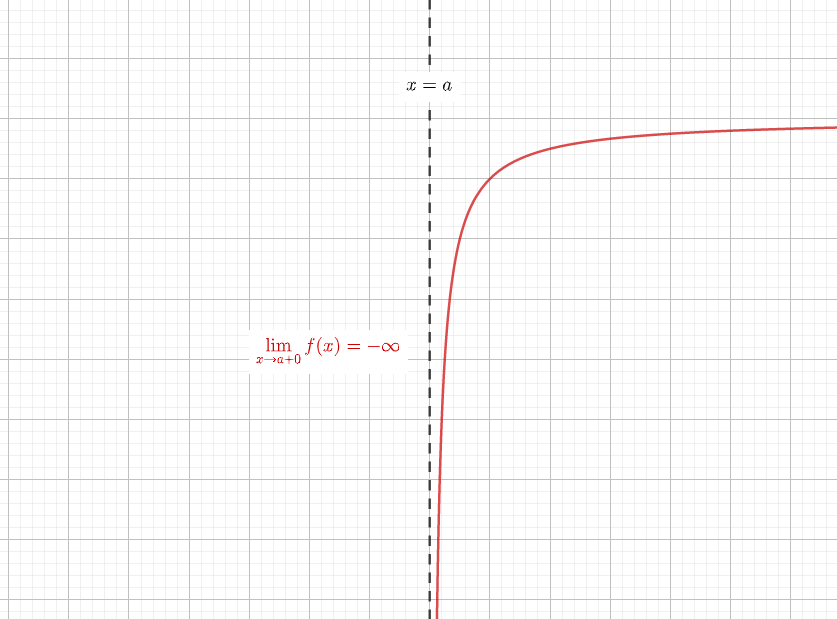
例題

$y=-\log (x-3)$は漸近線を持つか。

小春

対数関数だから、多分あるだろうなぁ・・・。

$$\lim_{x\to 3+0}f(x) = \infty$$

より、

$x=3$が漸近線

小春

ん？なんで$x\to3$を調べたの？漸近線だと見当がついてたの？

そうだよ！詳しくは後述する『漸近線の有無の判断方法』で紹介するね！

楓

$y$軸に平行でない漸近線の求め方2STEP

ある関数$f(x)$が$y$軸に平行でない直線$y=ax+b$を漸近線に持つとき、以下3STEPで求めます。

STEP1　$\frac{f(x)}{x}$の極限を調べる→傾きチェック

ある関数$f(x)$が直線$y=ax+b$を漸近線に持つとき、その距離はどこまでいっても（0に近づくけど）0にはなりません。

これを数学のことばで表すと、

$$\lim_{x\to\infty}\left\{\underbrace{f(x)-(ax+b)}_{2グラフ間の距離}\right\} =0 \cdots ①$$

とりあえず、$a$から求めたいので両辺$\frac{1}{x}$倍すると、

$$\lim_{x\to\infty}\left\{\frac{f(x)}{x}-a-\underbrace{\frac{b}{x}}_{\to 0}\right\} =0$$

となります。

つまり、$y=ax+b$が漸近線であるとき、

$$\lim_{x\to\infty}\left\{\frac{f(x)}{x}-a\right\} =0$$

が成り立つはずであり、

$$\lim_{x\to\infty}\left\{\frac{f(x)}{x}\right\} =a$$

より$\frac{f(x)}{x}$の極限値が、漸近線の傾きを表すとわかります。

STEP2　代入する

STEP1によりわかった極限値$a$の値を、①に代入すると

$$b=\lim_{x\to \infty} \left(f(x)-ax\right)$$

が成り立ちます。

つまり、$f(x)-ax$の極限を求めればOK。

漸近線の有無の判別方法

個人的な話ですが、理転したての頃、自信満々に描いたグラフに漸近線が描かれてなく、減点をもらいまくっていました。

「いやいや、じゃあいつ漸近線持ってるか調べればいいんだよ！」
「そもそも漸近線があるってわかってないと、調べなくないか？いつも忘れちゃうぞ。」

と、当時は不満だらけでした笑

結論から言えば、「いつ漸近線を調べればいいのか？」という態度自体が間違いです。

楓

漸近線は常に調べるべきってことね！

とは言え、簡易的な漸近線チェッカーがあるので、テクニックとして知っておくとよいでしょう。

楓

気楽に簡易チェッカーで試して、「あ、いるな？」と思ったらガッツリ計算して求めます。

チェック①　$y$軸に平行でない漸近線があるか

これは『$y$軸に平行でない漸近線の求め方』で紹介した方法を応用します。

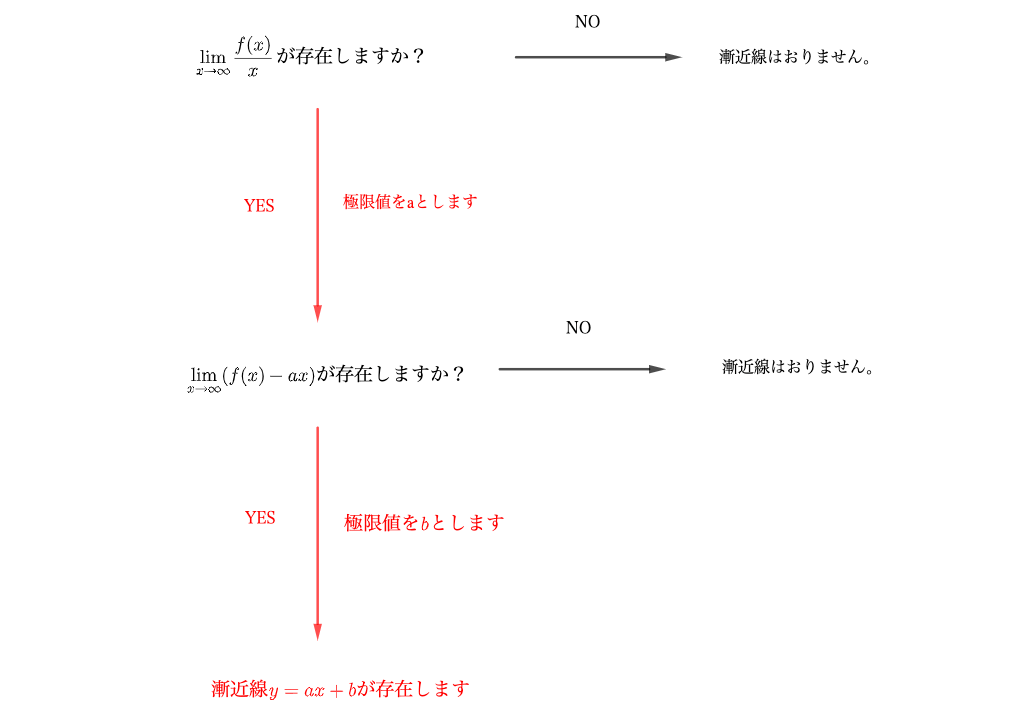
まず、

$$\lim_{x\to\infty}\left\{\frac{f(x)}{x}\right\} $$

を調べることで、傾きを持つかチェックします。

もしこの極限値が存在しないのであれば、その時点で$y$軸に平行でない漸近線は存在しません。

もし仮に

$$\lim_{x\to\infty}\left\{\frac{f(x)}{x}\right\} =a$$

となっていても、

$$b=\lim_{x\to \infty} \left(f(x)-ax\right)$$

となるような$b$が存在しない場合も、$y$軸に平行でない漸近線は存在しません。

つまりグラフを書いたときに、ちょろ〜っと$f(x)-ax$の極限を調べて、極限値がある場合は本腰入れて調べようって話！

チェック②　不連続な点がある

関数$y=\frac{1}{x}$は$x=0$にて不連続ですね。

このように定義域内で、$x=a$のときだけ連続ではない場合、$y$軸に平行な漸近線を持つ可能性があります。

楓

さっきの『$y$軸に平行な漸近線の求め方』で扱った例題は、$x=3$で不連続だよね？

なるほど、だから漸近線かもしれないって調べた感じか！

小春

もし不連続な点があるのなら、上述の『$y$軸に平行な漸近線の求め方』を使ってチェックしてみましょう。

チェック③　漸近線を持つ代表的な関数である

すでに紹介した漸近線を持つ有名関数の形をしているとき、漸近線がある可能性を疑いましょう。

以上が簡易チェッカーです。

漸近線はグラフを描く上で重要な指標になるので、常に考える癖を持ちましょう。

まとめ

今日のまとめをすると、

まとめ

漸近線は常に調べるべし。

漸近線を調べるためには、

$$\lim_{x\to\infty}\left\{\frac{f(x)}{x}\right\} $$の極限の有無を調べてから、
$$b=\lim_{x\to \infty} \left(f(x)-ax\right)$$の有無を調べれば良い。

また、不連続な点での極限を調べれば良い。

今日は長かったね！お疲れ様でした。

漸近線は極限の計算が必要なので、あまりしたくないかもしれませんが、常に「いるかも」と思っていてくださいね。

以上、「漸近線」についてでした。

チェック問題

例題

次の関数の中で漸近線を持つものはどれか。また、持つものは漸近線の方程式も求めよ。

$$y=\sqrt{x-2}$$
$$y=\frac{(x+1)^3}{x^2+2x}$$
$$y=\sqrt[3]{(x-1)(x-2)^2}$$

[1]について

この関数の定義域は$2≦x$。

$$\lim_{x\to 2+0}\sqrt{x-2} =0$$

より、$y$軸に並行な漸近線はない。

\begin{align} \lim_{x\to \infty}\frac{\sqrt{x-2}}{x} &= \lim_{x\to \infty}\sqrt{\frac{1}{x}-\frac{1}{x^2}}\\\ &= 0\\\ \end{align}

より、傾き0の漸近線がある可能性がある。

このとき切片を求めるためには

$$\lim_{x\to \infty}\left(\sqrt{x-2}-0\right)$$

を求めれば良い。

ところがこれは無限大に発散するため、極限値を持たない。

よって、この関数は漸近線を持たない。

[2]について

この関数は、定義域において$x=0,-2$のときのみ不連続となる。

よって$y$軸に平行な漸近線を持つ可能性があります。

$$\lim_{x\to -2-0} \frac{(x+1)^3}{x^2+2x} =-\infty$$
$$\lim_{x\to -2+0} \frac{(x+1)^3}{x^2+2x} =\infty$$
$$\lim_{x\to -0} \frac{(x+1)^3}{x^2+2x} =-\infty$$
$$\lim_{x\to +0} \frac{(x+1)^3}{x^2+2x} =\infty$$

より、$y$軸に平行な漸近線$x=0,-2$を持つ。

また、

\begin{align} \lim_{x\to \pm\infty} \frac{(x+1)^3}{x^2+2x}\times\frac{1}{x} &= \lim_{x\to \pm\infty} \frac{\left(1+\frac{1}{x}\right)^3}{1+\frac{1}{x}}\\\ &= 1\\\ \end{align}

より、傾き1の漸近線を持つ可能性もある。

このとき切片を求めるためには

$$\lim_{x\to \pm\infty}\left(\frac{(x+1)^3}{x^2+2x}-x\right)$$

を求めれば良い。

これを計算すると極限値は1となり、これは切片を表したので、$y=x+1$が漸近線であることがわかる。

よって$x=0,x=-2,y=x+1$が漸近線。

[3]について

この関数で非連続な点はなさそうなので、$y$軸に平行な漸近線はないと思われる。

\begin{align} \lim_{x\to\pm\infty}\sqrt[3]{(x-1)(x-2)^2}\times\frac{1}{x} &= \lim_{x\to\pm\infty}\left(1-\frac{1}{x}\right)^{\frac{1}{3}}\left(1-\frac{2}{x}\right)^{\frac{2}{3}}\\\ &= 1\\\ \end{align}

（※見切れている場合はスクロール）

より、傾き1の漸近線を持つ可能性がある。

このとき切片を求めるためには

$$\lim_{x\to \pm\infty}\left(\sqrt[3]{(x-1)(x-2)^2}-x\right)$$

を求めれば良い。

楓

はい、気合入れてください。

\begin{align} \lim_{x\to \pm\infty}\left(\sqrt[3]{(x-1)(x-2)^2}-x\right) &= \lim_{x\to \pm\infty}\left((x-1)^{\frac{1}{3}}(x-2)^{\frac{2}{3}}-x\right)\\\ &= \lim_{x\to \pm\infty}\frac{(x-1)(x-2)^2-x^3}{(x-1)^{\frac{2}{3}}(x-2)^{\frac{4}{3}}+x(x-1)^{\frac{1}{3}}(x-2)^{\frac{2}{3}}+x^2}\\\ &= \lim_{x\to\pm\infty}\frac{-5+\frac{8}{x}-\frac{4}{x^2}}{\left(1-\frac{1}{x}\right)^{\frac{2}{3}}\left(1-\frac{2}{x}\right)^{\frac{4}{3}}+\left(1-\frac{1}{x}\right)^{\frac{1}{3}}\left(1-\frac{2}{x}\right)^{\frac{2}{3}}+1}\\\ &= -\frac{5}{3} \end{align}

（※見切れている場合はスクロール）

小春

は、吐きそう・・・

よって、$y=x-\frac{5}{3}$を漸近線に持つ。

小春

漸近線には、計算力も必要ね。。。

【漸近線】を調べ忘れる君へ漸近線に必要な知識を徹底的にまとめてみました。

漸近線とは

漸近線を持つ代表的な関数

指数関数