【増減、凹凸を調べ、グラフを描け】意味を考えれば、凹凸グラフは迷わず解けるよ。

Today's Topic

よりリアルな（凹凸まで調べた）グラフを描くためには、

$f’(x),f’’(x)$を求め、
増減表を描き、
$f’(x),f’’(x)$の符号から曲がり方を判断すれば良い。
最後に漸近線チェックを行う。

楓

さて、今日は2階微分を用いたグラフの描き方を紹介するよ。この例題を元に、考えていこう！

例題

$f(x)=\frac{1}{x^2 +1}$のグラフを描け

う〜ん、微分するのめんどくさそうだけど・・・。

小春

この記事を読むと、この意味がわかる！

凹凸を調べるグラフの描き方のコツ
変曲点や凹凸の調べ方

楓

最後に練習問題もあるよ！

Contents

1 これまでの増減表では不十分
2 2階微分まで調べる意味
3 凹凸を調べ、描いたグラフ
4 変曲点
5 まとめ

これまでの増減表では不十分

では試しに1階微分を求めて、増減表を描いてみましょう。

なお、この微分には分数関数の微分法を使うと秒速で解けますね。

$$f’(x) = \frac{-2x}{\left(x^2+1\right)^2}$$

$f’(x)=0$のとき、$x=0$より、増減表は次のようになります。

$$x$$	$$\cdots$$	$$0$$	$$\cdots$$
$$f'(x)$$	$$+$$	$$0$$	$$-$$
$$f(x)$$	$$\nearrow$$	$$1$$	$$\searrow$$

では、グラフはこんな感じ・・・なのでしょうか？

小春

あれ、でも$f(x)$は負の値にはならないよね・・・？

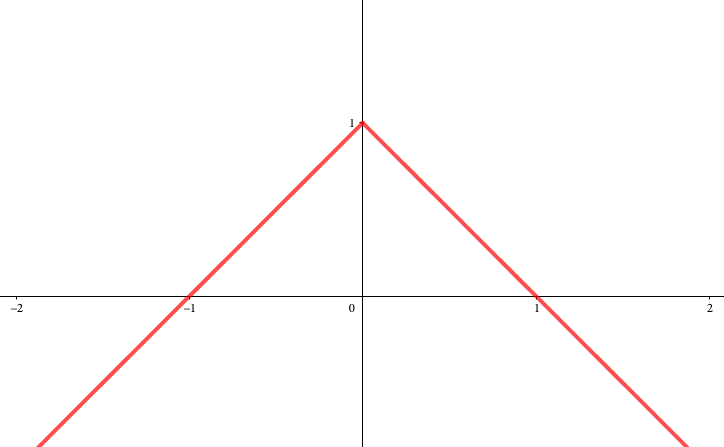
では実際のグラフと見比べてみましょう。

小春

え・・・、全然違うじゃん！

これなら小春がさっき言ったように、負の値にもなってないね！

楓

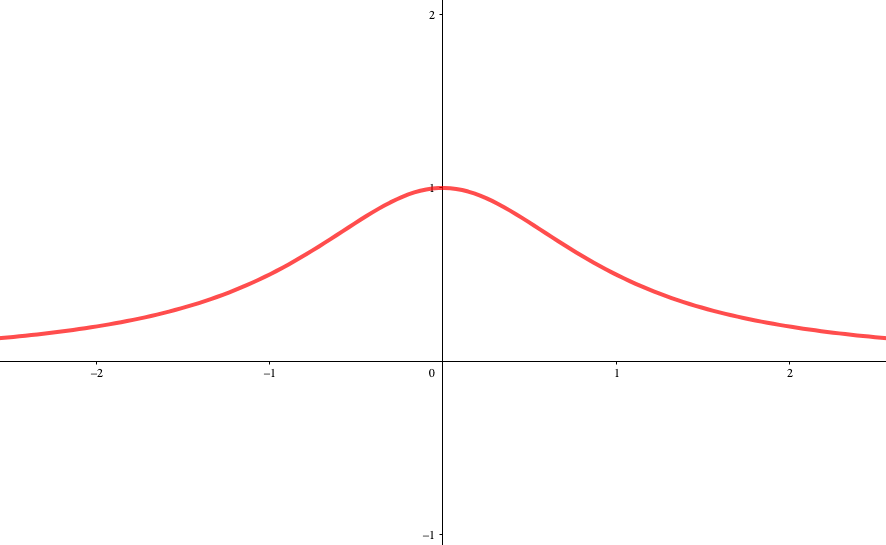
2階微分まで調べる意味

先ほど求めた増減表では極値はわかるので、「どこでカーブするのか」を知ることは可能です。

しかし、「どのようにカーブするのか」を全く考えていません。

楓

カーブの仕方は4通りあったね！

ということはどんなカーブをするか、調べる必要があるんだね。

小春

『グラフのカーブの仕方』については、こちらをご覧ください

: 【グラフの曲がり方】『グラフを描け』を最速で解くための最強スキルを公開。

続きを見る

2階微分の正負と、1階微分の正負を考えるとカーブの仕方は簡単にわかりましたね。

カーブの仕方一覧

1階微分の符号	$$+$$	$$-$$	$$+$$	$$-$$
2階微分の符号	$$-$$	$$+$$	$$+$$	$$-$$
グラフのカーブの仕方

楓

この表は暗記するのではなく、「なぜそのカーブを表すのか」をしっかりと理解しておこう！

以上のような理由から、（めんどくさいけど）2階微分までして、カーブの仕方を探っていくのです。

凹凸を調べ、描いたグラフ

それでは、カーブの仕方まで考えた「正確な解答」をみてみましょう。

$$f’(x) = \frac{-2x}{\left(x^2+1\right)^2}$$
$$f''(x) = \frac{6\left(x+\sqrt{\frac{1}{3}}\right)\left(x-\sqrt{\frac{1}{3}}\right)}{\left(x^2+1\right)^3}$$

$f’(x)=0$のとき、$x=0$、$f''(x)=0$のとき$x=\pm\sqrt{\frac{1}{3}}$なので、増減表は以下のようになる。

$$x$$	$$\cdots$$	$$-\sqrt{\frac{1}{3}}$$	$$\cdots$$	$$0$$	$$\cdots$$	$$\sqrt{\frac{1}{3}}$$	$$\cdots$$
$$f'(x)$$	$$+$$	$$+$$	$$+$$	$$0$$	$$-$$	$$-$$	$$-$$
$$f''(x)$$	$$+$$	$$0$$	$$-$$	$$-$$	$$-$$	$$0$$	$$+$$
$$f(x)$$		$$\frac{3}{4}$$		$$1$$		$$\frac{3}{4}$$

小春

2階微分まで含めたパワーアップした増減表を考えればいいんだね！

そして$f’(x),f''(x)$の符号を見比べて、カーブのしかたを書けばOK。グラフもあっという間だよ！

楓

増減表より、与えられた方程式のグラフは、次のようになる。

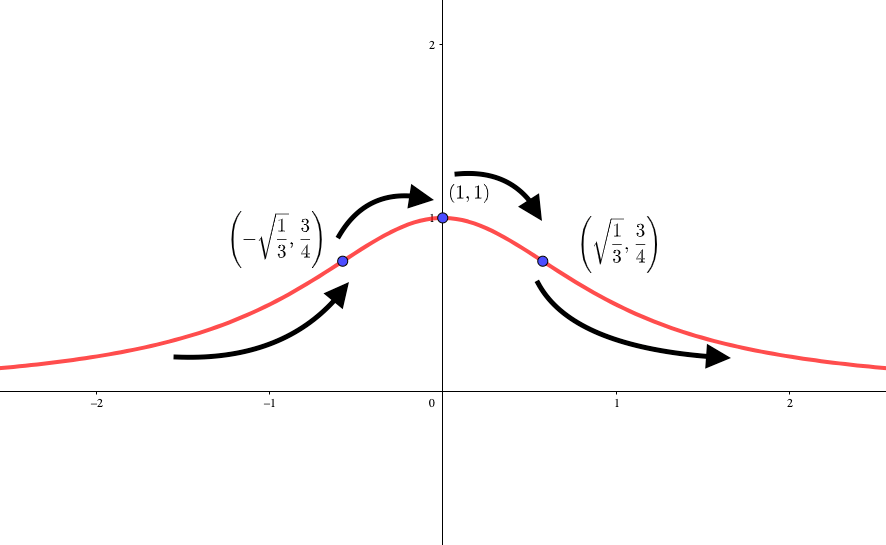
ちなみに、漸近線は必ず調べておきましょう。

漸近線の調べ方とタイミングはこちらを参考にしてください。

: 【漸近線】を調べ忘れる君へ漸近線に必要な知識を徹底的にまとめてみました。

続きを見る

\begin{align}\lim_{x\to+ \infty}f(x) &= \underbrace{\frac{1}{\infty}}_{ここは書かない}\\\ &= 0\\\ \end{align}
\begin{align}\lim_{x\to+ \infty}f(x) &= \underbrace{-\frac{1}{\infty}}_{ここは書かない}\\\ &= 0\\\ \end{align}

小春

あ、$y=0$が漸近線だね！

極限を調べて漸近線であることがわかったら、解答にもしっかり書いておこう！

楓

変曲点

先ほどの例題の$x=\pm\sqrt{\frac{1}{3}}$のように、2階微分の符号が切り替わる点を変曲点と言います。

よく$f''(x)=0$を満たす点を変曲点と勘違いしている人がいますが、これは正しくありません。

あくまで2階微分の符号が切り替わる点を変曲点というのであり、$f’‘(x)=0$を満たしてもその前後で符号が切り替わっていない場合は変曲点ではありません。

変曲点には面白い性質がいくつかあるので、別記事で詳しく語りますね！

まとめ

楓

最後にまとめをしておきます。

まとめ

よりリアルな（凹凸まで調べた）グラフを描くためには、

$f’(x),f’‘(x)$を求め、
増減表を描き、
$f’(x),f’’(x)$の符号から曲がり方を判断すれば良い。
最後に漸近線チェックを行う。

結局、新しい知識は何もなくて、ただ曲がり方を調べてねって話です。

この曲がり方が意識できるようになれば、どんなグラフ描画問題も怖くありません。

いくつか問題を解いて、慣れておくようにしましょう。

以上、「凹凸を調べたグラフの描き方」についてでした。

チェック問題

例題

次の関数の増減、凹凸、漸近線を調べ、グラフを描け。

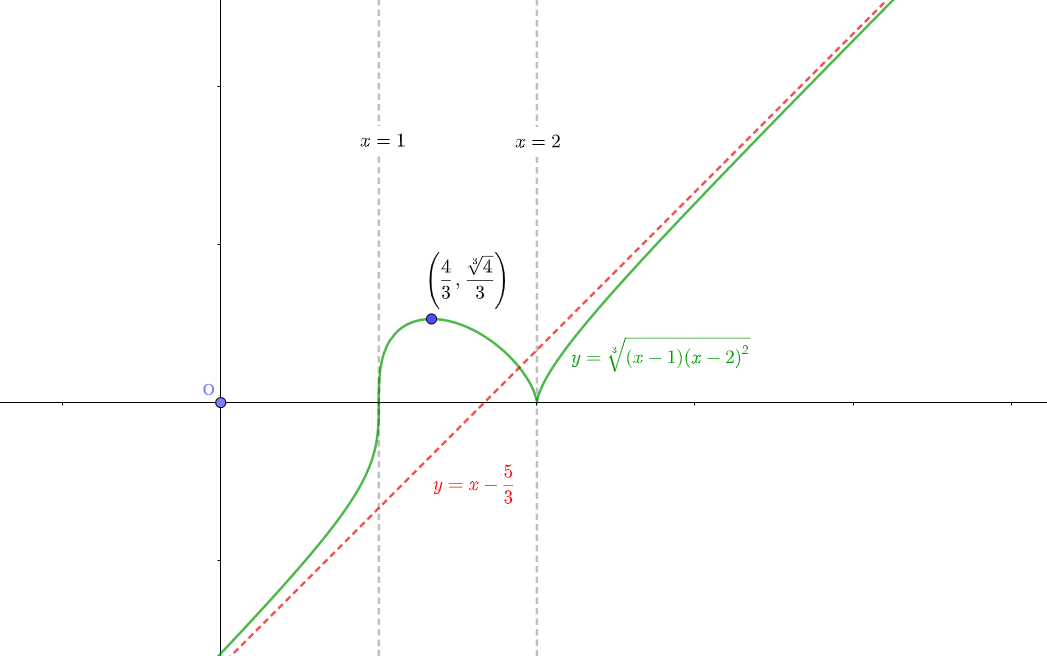
$$y= \sqrt[3]{(x-1)(x-2)^2}$$

楓

こういう問題は微分力が必要！効率的・かつ簡単に微分する工夫をしようね！

$y=(x-1)^{\frac{1}{3}}(x-2)^{\frac{2}{3}}$なので、1階微分・2階微分を求めると次のようになる。

\begin{align} y' &=\underbrace{ \frac{1}{3}(x-1)^{-\frac{2}{3}}(x-2)^{\frac{2}{3}}+\frac{2}{3}(x-1)^{\frac{1}{3}}(x-2)^{-\frac{1}{3}}}_{積の微分法}\\\ &= \frac{1}{3}(x-1)^{-\frac{2}{3}}(x-2)^{-\frac{1}{3}}(3x-4)\\\ \end{align}

\begin{align} y'' &= -\frac{2}{3}(x-1)^{-\frac{5}{3}}(x-2)^{-\frac{1}{3}}(3x-4)\\\ &　+ (x-1)^{-\frac{2}{3}}\cdot\left(- \frac{1}{3}\right)(x-2)^{-\frac{4}{3}}(3x-4)\\\ &　+ (x-1)^{-\frac{2}{3}}(x-2)^{-\frac{1}{3}}\cdot 3\\\ &=-\frac{2}{9}(x-1)^{-\frac{5}{3}}(x-2)^{-\frac{4}{3}} \end{align}

（※見切れている場合はスクロール）

小春

かえで・・くん・・、吐きそぅ・・うぷっ

ぎゃああああああああああ！

楓

$y'=0$のとき、$x=\frac{4}{3}$。

$y''=0$のときはない。

よって、増減表は次のようになる。

$$x$$	$$\cdots$$	$$1$$	$$\cdots$$	$$\frac{4}{3}$$	$$\cdots$$	$$2$$	$$\cdots$$
$$y'$$	$$+$$	$$×$$	$$+$$	$$0$$	$$-$$	$$×$$	$$+$$
$$y''$$	$$+$$	$$×$$	$$-$$	$$-$$	$$-$$	$$×$$	$$-$$
$$y$$		$$0$$		$$\frac{\sqrt[3]{4}}{3}$$		$$0$$

楓

$x=1,2$のときのような値を取れない$x$の値のときも調べるといいよ！

ここで漸近線について調べる。

この関数で非連続な点はなさそうなので、$y$軸に平行な漸近線はないと思われる。

\begin{align} \lim_{x\to\pm\infty}\sqrt[3]{(x-1)(x-2)^2}\times\frac{1}{x} &= \lim_{x\to\pm\infty}\left(1-\frac{1}{x}\right)^{\frac{1}{3}}\left(1-\frac{2}{x}\right)^{\frac{2}{3}}\\\ &= 1\\\ \end{align}

（※見切れている場合はスクロール）

より、傾き1の漸近線を持つ可能性がある。

このとき切片を求めるためには

$$\lim_{x\to \pm\infty}\left(\sqrt[3]{(x-1)(x-2)^2}-x\right)$$

を求めれば良い。

\begin{align} \lim_{x\to \pm\infty}\left(\sqrt[3]{(x-1)(x-2)^2}-x\right) &= \lim_{x\to \pm\infty}\left((x-1)^{\frac{1}{3}}(x-2)^{\frac{2}{3}}-x\right)\\\ &= \lim_{x\to \pm\infty}\frac{(x-1)(x-2)^2-x^3}{(x-1)^{\frac{2}{3}}(x-2)^{\frac{4}{3}}+x(x-1)^{\frac{1}{3}}(x-2)^{\frac{2}{3}}+x^2}\\\ &= \lim_{x\to\pm\infty}\frac{-5+\frac{8}{x}-\frac{4}{x^2}}{\left(1-\frac{1}{x}\right)^{\frac{2}{3}}\left(1-\frac{2}{x}\right)^{\frac{4}{3}}+\left(1-\frac{1}{x}\right)^{\frac{1}{3}}\left(1-\frac{2}{x}\right)^{\frac{2}{3}}+1}\\\ &= -\frac{5}{3} \end{align}

（※見切れている場合はスクロール）

よって、$y=x-\frac{5}{3}$を漸近線に持つ。

これをもとにグラフを描くと、このようになる。