【合成関数の微分法】のコツと証明→「約分」感覚でOK！小学生もできます。

Today's Topic

$$\frac{dy}{dx}=\frac{dy}{du}\times\frac{du}{dx}$$

楓

はい、じゃあ今日は合成関数の微分法を、逃げるな！

だってぇ、関数の関数の微分とか、下手くそな日本語みたいじゃん！絶対難しい！

小春

楓

それがそんなことないんだ。それにここを抑えると、暗記物がグッと減るんだよ。

えっ、そうなの！教えて！！

小春

楓

現金な子だなぁ・・・

▼復習はこちら

: 合成関数って、結局なんなんですか？要点だけを徹底マスター！

続きを見る

この記事を読むと・・・

合成微分のしたいことがわかる！
合成微分を簡単に計算する裏ワザを知ることができる！

Contents

1 合成関数講座｜合成関数の微分公式
- 1.1 合成関数の微分法のコツ
2 合成関数の微分法の証明
3 合成関数講座｜まとめ

合成関数講座｜合成関数の微分公式

楓

合成関数の最重要ポイント、それが合成関数の微分だ！

まずは、合成関数を微分するとどのようになるのか見てみましょう。

合成関数の微分

2つの関数$y=f(u),u=g(x)$の合成関数$f(g(x))$を$x$について微分するとき、微分した値$\frac{dy}{dx}$は

$\frac{dy}{dx}=\frac{dy}{du}\times\frac{du}{dx}$

と表せる。

小春

本当に、分数の約分みたい！

その通り！まずは例題を通して、この微分法のコツを勉強しよう！

楓

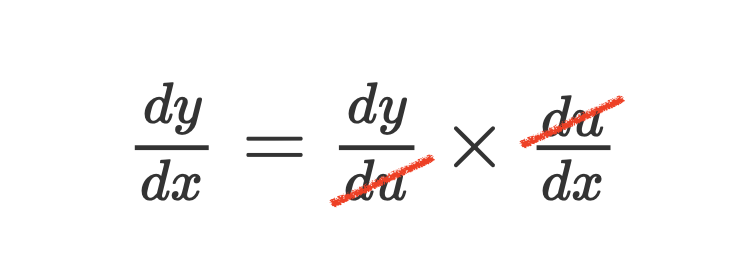
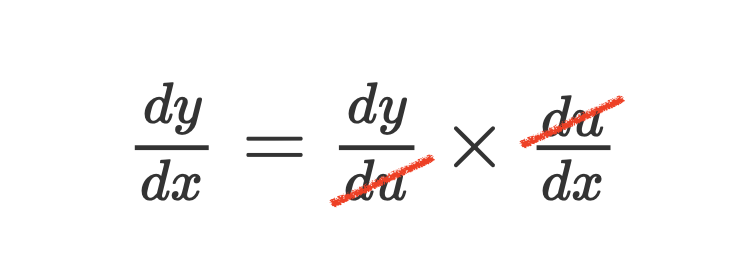
合成関数の微分法のコツ

はじめにコツを紹介しておきますね。

合成関数の微分のコツ

合成関数の微分をするためには、

合成されている2つの関数をみつける。
それぞれ微分する。
微分した値を掛け合わせる。

の順に行えば良い。

それではいくつかの例題を見ていきましょう！

例題1

例題

合成関数$y=(2x+1)^3$を微分せよ。

これは$y=u^3, u=2x+1$の合成関数。

よって

\begin{align} \frac{dy}{dx} &= \frac{dy}{du}\cdot \frac{du}{dx}\\\ &= 3u^2\cdot u'\\\ &= 6(2x+1)^2\\\ \end{align}

楓

外ビブン×中ビブンと考えることもできるね！

例題2

例題

合成関数$y= \frac{1}{\cos x}$を微分せよ。

これは$y=u^{(-1)}, u=\cos x$の合成関数。

よって

\begin{align} \frac{dy}{dx} &= \frac{dy}{du}\cdot \frac{du}{dx}\\\ &= -u^{(-2)}\cdot u'\\\ &= \frac{\sin x}{\cos^2 x}\\\ \end{align}

例題3

例題

合成関数$y= \log \left({3x^2+1}\right)$を微分せよ。

これは$y=\log u, u=3x^2+1$の合成関数。

よって

\begin{align} \frac{dy}{dx} &= \frac{dy}{du}\cdot \frac{du}{dx}\\\ &= \frac{1}{u}\cdot u'\\\ &= \frac{6x}{3x^2+1}\\\ \end{align}

合成関数の微分法の証明

2つの関数$y=f(u), u=g(x)$を考えます。

合成関数$y=f(g(x))$を$x$で微分した$\frac{dy}{dx}$を、導関数の定義から証明していきますね。

\begin{align} \frac{dy}{dx} &= \lim_{h\to 0}\frac{f(g(x+h))-f(g(x))}{(x+h)-x}\\\ \end{align}

しかしこのままだと意味が分からないので、次のような意図的な変形を施します。

\begin{align} \frac{dy}{dx} &= \lim_{h\to 0}\frac{f(g(x+h))-f(g(x))}{(x+h)-x}\\\ &= \lim_{h\to 0}\frac{f(g(x+h))-f(g(x))}{\color{red}{g(x+h)-g(x)}}\cdot \frac{\color{red}{g(x+h)-g(x)}}{(x+h)-x}\\\ \end{align}

（※見切れている場合はスクロール）

ポイント

式$\frac{A}{B}$について考えるとき、

$$\frac{A}{C}\cdot\frac{C}{B}$$

のように、無理やりCを作ることで式が考えやすくなることがある。

小春

$\frac{1}{C}\cdot \frac{C}{1} = 1$だから式の整合性はOKなのね！

この変形により、リミットを分配してあげると

\begin{align} &\ \ \ \ \lim_{h\to 0}\frac{f(g(x+h))-f(g(x))}{g(x+h)-g(x)}\cdot \lim_{h\to 0 }\frac{g(x+h)-g(x)}{h}\\\ &= \frac{d}{dg(x)}f(g(x))\cdot\frac{d}{dx}g(x)\\\ \end{align}

（※見切れている場合はスクロール）

となります。

$u=g(x)$なので、

$$\frac{dy}{dx}= \frac{dy}{du}\cdot\frac{du}{dx}$$

が示せました。

楓

まぁ、厳密には間違ってるんだけどね。

えっ・・・。

小春

楓

厳密verは大学でやるけど、正確な反面、かなりわかりにくい。

なるほど、高校範囲だとここまでで十分ってことね…。

小春

合成関数講座｜まとめ

最後にまとめです！

まとめ

合成関数$f(g(x))$の微分を考えるためには、合成されている2つの関数$y=f(t),t=g(x)$をそれぞれ微分してかければ良い。
外側の関数$y=f(t)$の微分をした後に、内側の関数$t=g(x)$の微分を掛け合わせたものともみなせる！

小春

外ビブン×中ビブンと覚えてもいいね

以上のように、合成関数の微分は合成されている2つの関数を見破ってそれぞれ微分した方が簡単に終わります。

今後重要な位置を占めてくる微分法なので、ぜひ覚えておきましょう。

以上、「合成関数の微分公式について」でした。

【合成関数の微分法】のコツと証明→「約分」感覚でOK！小学生もできます。

合成関数って、結局なんなんですか？要点だけを徹底マスター！

合成関数講座｜合成関数の微分公式

合成関数の微分法のコツ

例題1

例題2

例題3

合成関数の微分法の証明

合成関数講座｜まとめ

【微分公式一覧】証明や差がつくポイント、役立つテクニックなど総まとめ

【感覚で理解できる！】常用対数とは？意味と使い方を徹底解説！！

自然対数、ネイピア数とは？なぜあの定義なのか、何が自然なのか。お金の話で超簡単に理解できる！！

【指数関数の定義】なぜ底が負のときは定義しないのか→ダルいから

【整数の指数法則】なぜ0乗が1なのか、息をするようにわかる指数法則