合成関数って、結局なんなんですか？要点だけを徹底マスター！

小春

合成関数って何。。。難しそう。。。

簡単にいうと、これまで扱ってきた関数\(y=f(x)\)の\(x\)も何かしらの関数になっている場合のことを考えているよ。

楓

小春

関数in関数ってこと？

そゆこと！とても面白い性質があるんだ。

楓

小春

じゃあ今日は、合成関数をマスターさせて欲しいな！

合成関数講座｜そもそも関数とは

楓

合成関数について考える前に、まず関数について理解していないのでは？

関数は中学校の頃から導入されますが、あなたは関数とは一体何か説明できますか？

もし説明できるのであれば十分です、この章は読み飛ばしちゃってください！

一方で「方程式と区別がつかなかったなぁ」なんていう人は、そもそも関数の意味が理解できていません。

まずは関数の定義を確認しましょう。

図で表すとこのようになります。

楓

集合\(X\)に属する\(x\)が、関数\(f\)によって集合\(Y\)に属する\(y\)と唯一結びつくときを関数といい、\(y=f(x)\)と表せるよ。

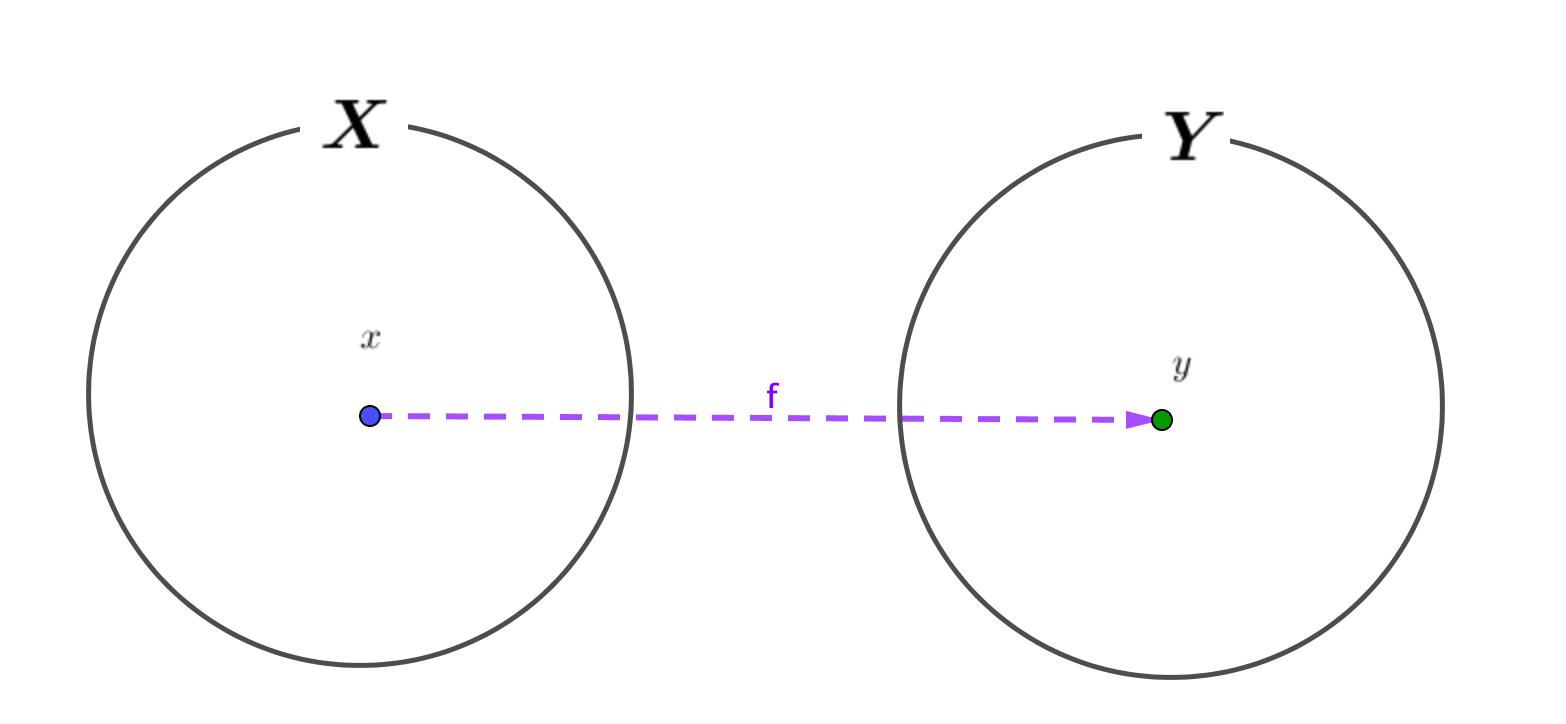
関数でない例

すなわち、\(x\)の値を1つ代入して、答えが1つでないものは関数ではありません。

例えば、円の方程式\(x^2+y^2=1\)は\(x\)の値を適当に1つ代入したとき、\(y\)の値が2つ定まることがあるので関数ではありません。

小春

\(x=\frac{1}{2}\)を円の方程式に代入すると\(y=\pm\frac{\sqrt{3}}{2}\)となるから、解が2つあるとわかるね。

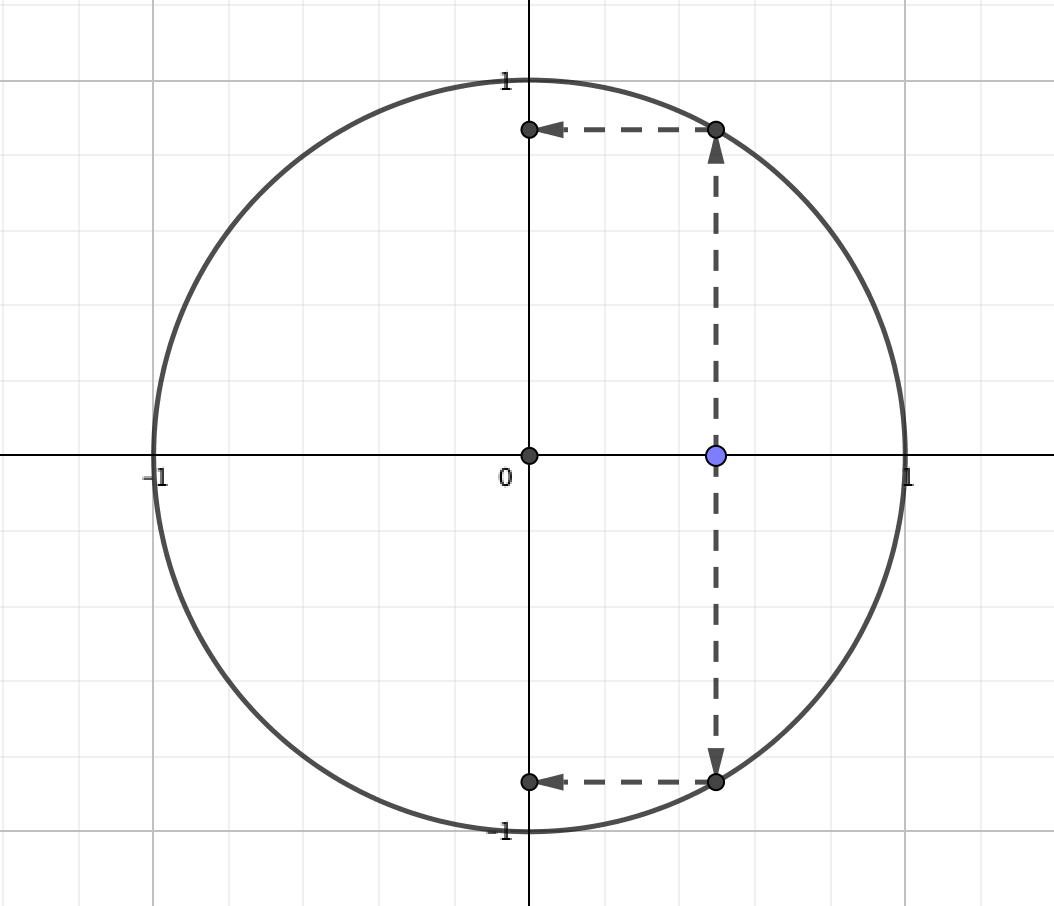
独立変数・従属変数

続いて言葉のお勉強。

\(y\)が\(x\)の関数であるとき、

と言います。

楓

またこのとき、\(y\)は\(x\)に依存する、とも言うよ！

イメージしやすいように言うと、英語では

と言いますよ。

楓

日本語堅苦しくて僕は嫌いです。

英語の方がわかりやすいね笑

小春

合成関数講座｜合成関数の意味と考え方

楓

復習が済んだところで、合成関数の話に入ろう！

関数の意味がわかれば、合成関数の意味の把握は難しくありません。

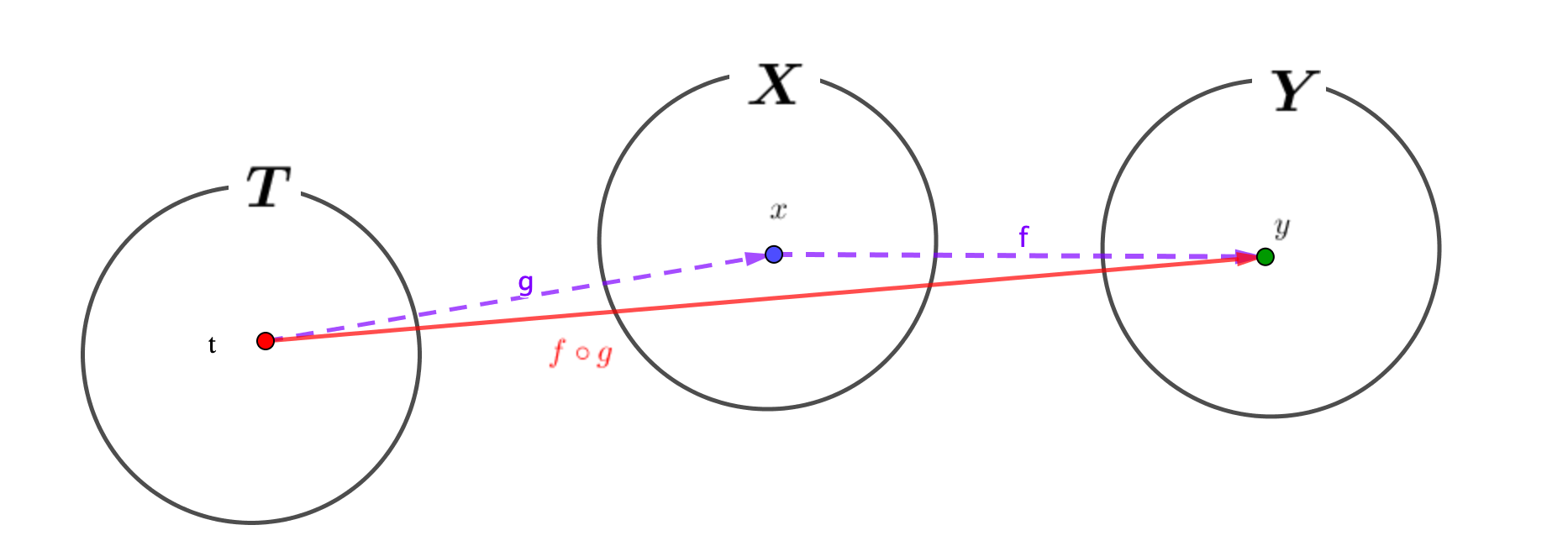
\(x\)が\(t\)の関数\(x=g(t)\)、\(y\)が\(x\)の関数\(y=f(x)\)の場合を考えてみましょう。

\(x\)は\(t\)に依存し、その\(x\)に\(y\)は依存するわけですから、当然\(y\)は\(t\)に依存します。

小春

つまり\(y\)は\(t\)の関数というわけだね！

このように関数\(y=f(x)\)の独立変数\(x\)もまた、関数\(x=g(x)\)と表されるとき、\(y=f(g(t))\)と書き\(y\)と\(t\)の合成関数と言います。

\(f(g(t))\)を\(\left(f\circ g\right)(t)\)と書くこともありますが、それは図の赤線のようにショートカットした矢印のことを指しています。

具体的な例題を見てみましょう。

楓

そもそも\(f(a)\)の値は？

\(f(a)=a^2\)でしょ？

小春

楓

じゃあ\(f(a+b)\)は？

\(f(a+b)=(a+b)^2\)でしょ？それくらいわかるよ・・・

小春

楓

じゃあ\(f(g(x))\)は？

えっと、、、これ？

小春

楓

その通り！

ご覧の通り、合成関数の演算は独立変数\(x\)を関数\(g(x)\)に書き換える作業、もしくは代入とみなすことができます。

合成関数の例

具体的な合成関数をみて、もっと合成関数の感覚を育てましょう。

（例1）\(y=(2x+1)^2\)

この関数は、\(y=u^2\)の独立変数\(u\)が、関数\(u=2x+1\)に書き換わっているとみることができます。

よって合成関数であることがわかります。

（例2）\(y=\sin(3x+1)\)

この関数は\(y=\sin\theta\)の独立変数\(\theta\)が、関数\(\theta=3x+1\)に書き換わっているとみることができます。

よって合成関数であることがわかります。

楓

慣れてきたかな？もう2つやってみよう！

（例3）\(y=\log (\frac{1}{2}x)^3\)

この関数は\(y=\log u\)の独立変数\(u\)が、関数\(u=\left(\frac{1}{2}x\right)^3\)に書き換わっているとみることができます。

またこの関数\(u\)も\(u=v^3\)の独立変数\(v\)が関数\(v=\frac{1}{2}x\)に書き換わっているとみることができます。

よって3つの関数の合成関数であることがわかります。

（例4）\(y=\log \left(-\frac{1}{2}|x|\right)\)

この関数は\(y=\log u\)の独立変数\(u\)が、関数\(u=-\frac{1}{2}|x|\)に書き換わっていると見なせます。

ところが、関数\(u\)の値は常に負となり、その\(u\)を自然対数の真数とすることはできません（真数条件）。

つまり合成関数ではあるが、定義はできないということです。

楓

合成関数にできないのではなく、できたけど存在しないのです。

合成関数講座｜まとめ

最後にまとめです！

合成関数は、関数の基本的な知識があれば全く難しくありませんね。

今後重要な位置を占めてくる関数なので、ぜひ覚えておきましょう。

以上、「合成関数について」でした。