Today's Topic
$$(a+bi)+(c+di)=(a+c)+(b+d)i$$
$$(a+bi)-(c+di)=(a-c)+(b-d)i$$
$$(a+bi)\cdot(c+di)=(ac-bd)+(ad+bc)i$$
$$\frac{a+bi}{c+di}=\frac{ac+bd}{c^2+d^2}+\frac{bc-ad}{c^2=d^2}i$$





こんなあなたへ
「複素数の図形的な意味について知りたい!」
「図的なイメージを身に付けたい!」
この記事を読むと、この意味がわかる!
- 点\(A(3+i)\)を、原点中心に\(-\frac{\pi}{2}\)だけ回転させた点\(B(\beta)\)を求めよ。

複素数を一気に理解したい方への記事は、こちらにまとめてあります。
複素数の四則まとめ
最初に複素数の足し算から割り算までの、四則演算の公式をまとめておきます。
ポイント
$$(a+bi)+(c+di)=(a+c)+(b+d)i$$
$$(a+bi)-(c+di)=(a-c)+(b-d)i$$
$$(a+bi)\cdot(c+di)=(ac-bd)+(ad+bc)i$$
$$\frac{a+bi}{c+di}=\frac{ac+bd}{c^2+d^2}+\frac{bc-ad}{c^2=d^2}i$$
(※見切れている場合はスクロール)


この記事では、この公式を覚えるよりも上の、図的なイメージができるレベルを目指します。
複素数の和・差・実数倍|ベクトルを意識しよう
ここではベクトルの表記を
$$\overrightarrow{a}=\begin{pmatrix}a\\ b\\ \end{pmatrix}$$
のようにしています。座標と区別しやすいためですので、許してぴ❤︎
まずは準備運動から。
複素数は前提として、ベクトルを意識すると図形的なイメージに発展しやすくなります。
ここではまず、ベクトルの意識が定着しやすい、足し算・引き算、そして実数倍について見て行きます。
横軸に実数\(x\)を、縦軸に純虚数\(yi\)をとって、複素数\(x+yi\)を平面状に描く複素平面というものを考えます。
この座標系で\(1+i\)をプロットすると、このようになります。
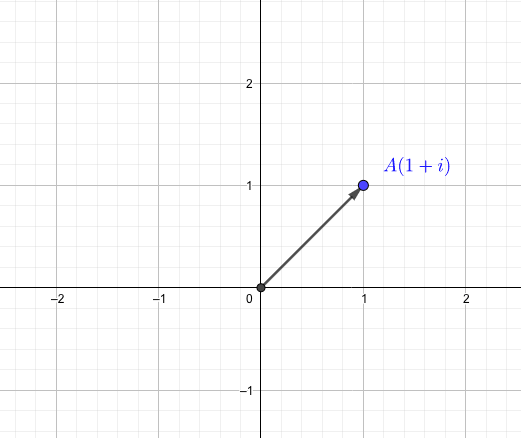



ポイント
複素数\(a+bi\)は、複素平面上でベクトル\(\begin{pmatrix}a\\ b\\ \end{pmatrix}\)を描く。
このイメージの元、2つの複素数の和と差を考えて見ましょう。
\begin{align} (1+i)-(-1+2i) &= (1+1)+(1-2)i\\\ &= 2-i\\\ \end{align}
(※見切れている場合はスクロール)
4点\(A(1+i),B(-1+2i),C(0+3i),D(2-i)\)を複素平面上に描くと、このような関係になっています。
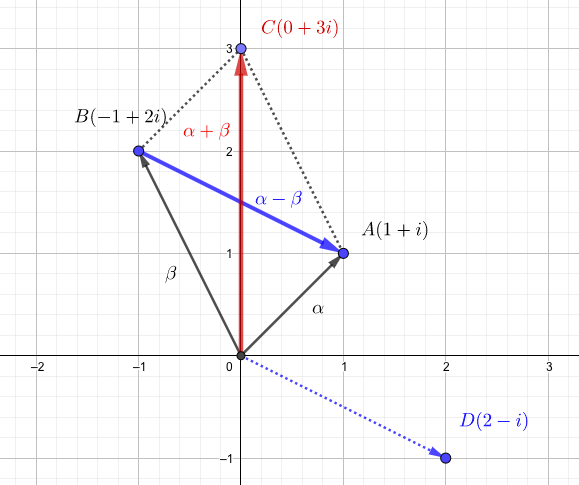



次に実数倍を考えて見ましょう。
$$3(1+i)=3+3i$$
\(A(1+i),B(3+3i)\)をプロットしてみると、
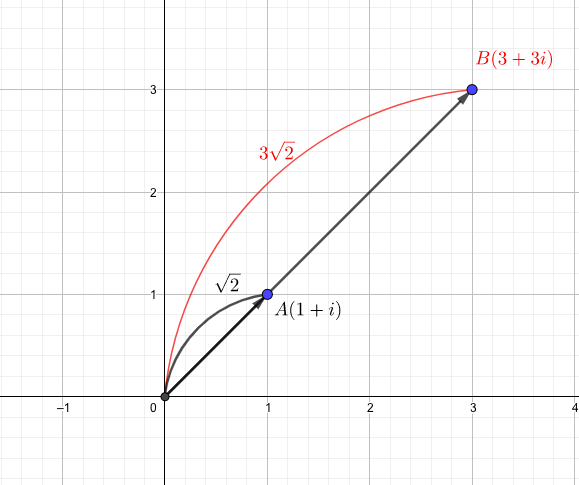



複素数の積|極形式に持って行こう
複素数の積は、図形的な意味合いがとても特徴的です。
その意味合いを捉えるために、まずは極形式という考え方を身につけましょう。
極形式について復習したい人はこちらを参考にしてください。
続きを見る



極形式に変形するコツと、変形すべき場面→距離と偏角を意識した図を見る
2つの複素数の積を、極形式の形で見てみることにしましょう。
\(\gamma\)を\(\alpha,\ \beta\)の積
\begin{align} \gamma &= \left(\sqrt{3}+i\right)\cdot(\sqrt{3}+3i) \\\ &= 0+4\sqrt{3}i\\\ \end{align}
とし、3つそれぞれ極形式で表すと、
$$\alpha = 2(\cos \frac{\pi}{6}+i\sin\frac{\pi}{6})$$
$$\beta = 2\sqrt{3}(\cos \frac{\pi}{3}+i\sin\frac{\pi}{3})$$
$$\gamma = 4\sqrt{3}(\cos \frac{\pi}{2}+i\sin\frac{\pi}{2})$$
となる。
この3つの複素数を複素平面上にプロットすると、こうなります。
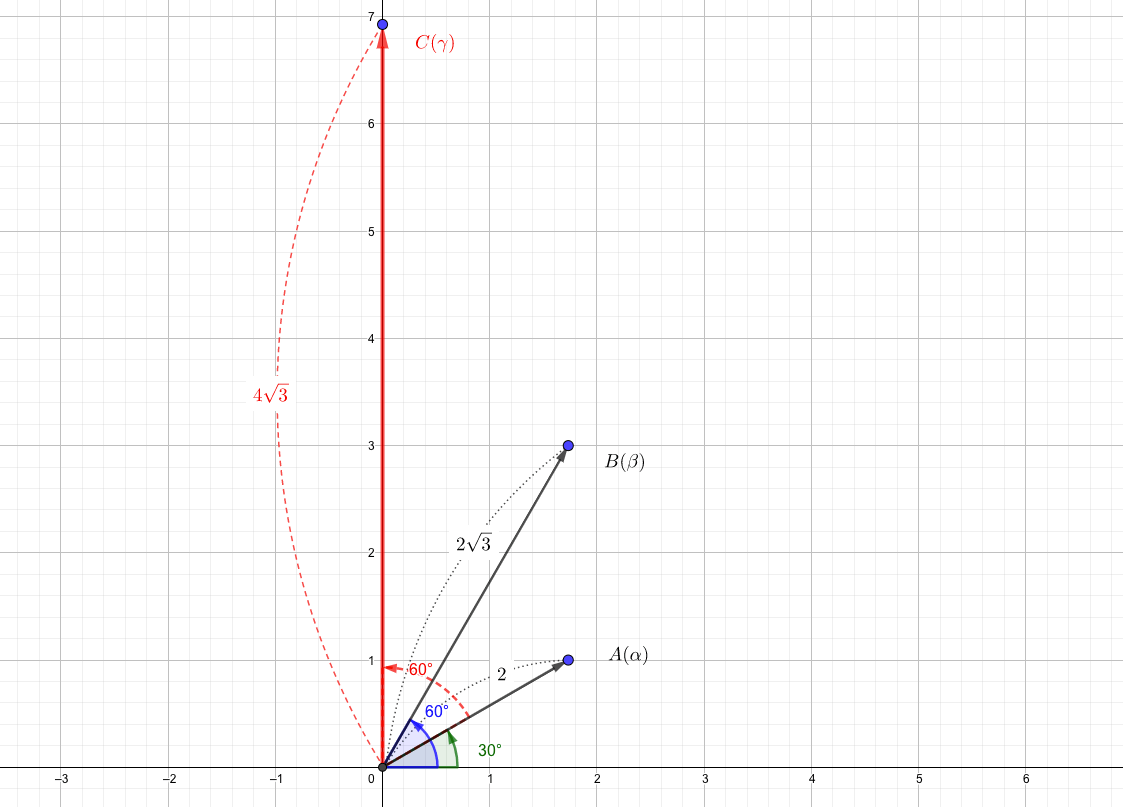

\(\gamma\)について調べると、
- 長さ:\(\alpha\)の長さが、\(\beta\)の長さ倍された。
- 偏角:\(\alpha\)の偏角から、\(\beta\)の偏角だけ進めた。
よって、次のことがわかります。
ポイント
2つの複素数\(\alpha,\beta\)について、積\(\alpha\beta\)は
- \(\alpha\)の長さを、\(\beta\)の長さ倍する
- \(\alpha\)の偏角を、\(\beta\)の偏角だけ進める
ちなみに複素数の形\(a+bi\)と極形式の形\(r\left(\cos\theta+i\sin\theta\right)\)について、
- 複素数の形:計算しやすい
- 極形式の形:図形的にイメージしやすい
という使い分けがあることも押さえておきましょう。
循環する複素数の積
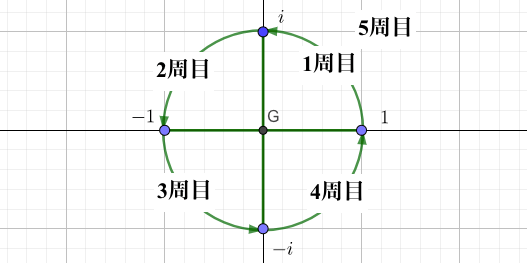
複素数\(0+i=i\)を考えて見ましょう。
$$i^2=-1$$
$$i^3=-i$$
$$i^4=1$$
$$i^5=i$$
となることから、\(i\)は5回かけると元に戻ってくることがわかります。






これも図形的に考えると、また違った景色が見えます。
\(0+i \)を極形式で考えると
ですので、ド・モアブルの定理より
$$i^n = \cos\frac{n}{2}\pi+i\sin\frac{n}{2}\pi\ .$$
これをみると、偏角が\(\frac{n}{2}\pi\)、つまり「\(90^{\circ}\)の○倍」であることがわかります。
偏角は回転する角度を表すので、
- \(i^2\)→\(\frac{2}{2}\pi\)回転
- \(i^3\)→\(\frac{3}{2}\pi\)回転
- \(i^4\)→\(\frac{4}{2}\pi\)回転
- \(i^5\)→\(\frac{5}{2}\pi\)回転
となり、5回転目に元に戻ってくるイメージと一致しますね。

複素数の商|回転方向を意識しよう
おまけで、複素数の商について考えましょう。
割り算は、逆数の掛け算で考えることができるので、結局は複素数の積に帰着して考えることができます。
\begin{align} \gamma &= \frac{\left(\sqrt{3}+i\right)}{(\sqrt{3}+3i)} \\\ &= \frac{\left(\sqrt{3}+i\right)\color{red}{\times (\sqrt{3}-3i)}}{(\sqrt{3}+3i)\color{red}{\times (\sqrt{3}-3i)}}\\\ &= \frac{1}{2}-\frac{\sqrt{3}}{6}i\\\ \end{align}




共役な複素数について復習したい人はこちらを参考にしてください。
続きを見る



共役な複素数の重要性質4つ→特殊計算・分割可能・方程式の解・複素平面
それぞれ極形式で表すと、
$$\beta = 2\sqrt{3}(\cos \frac{\pi}{3}+i\sin\frac{\pi}{3})$$
$$\gamma = \frac{\sqrt{3}}{3}\left(\cos \left(-\frac{\pi}{6}\right)+i\sin\left(-\frac{\pi}{6}\right)\right)$$
となります。
この3つを図にプロットすると、
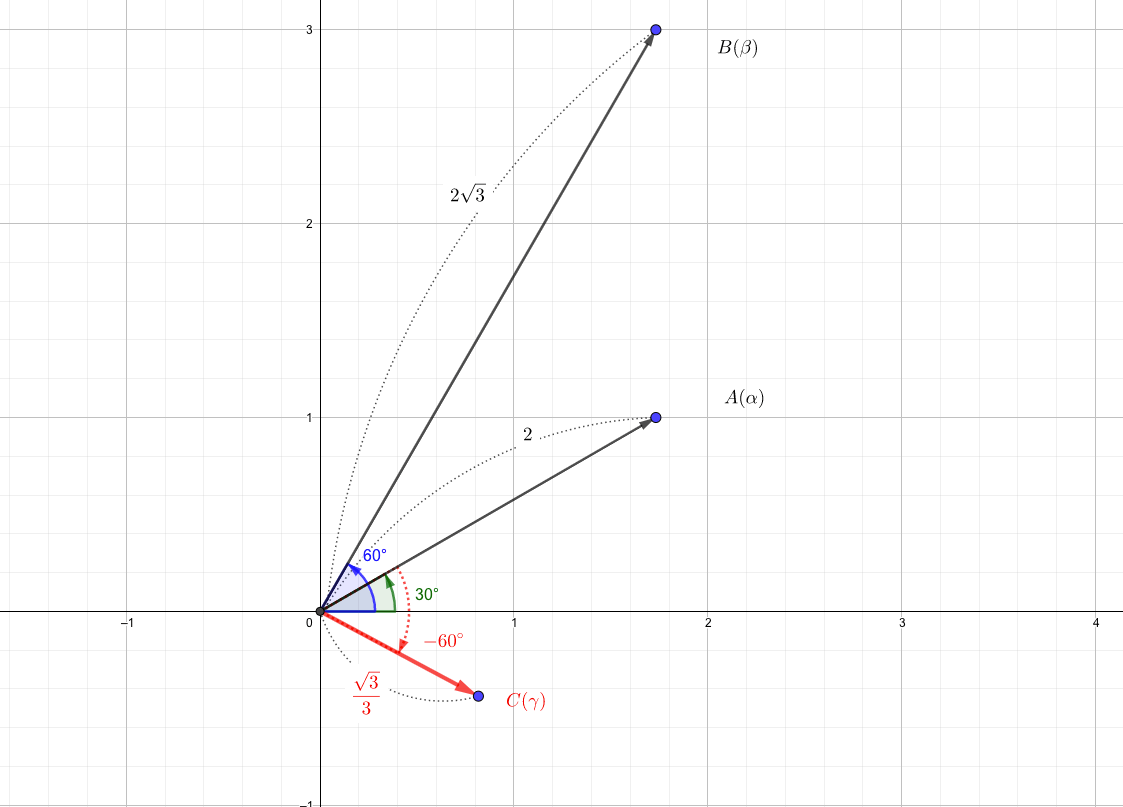

\(\gamma\)について調べると、
- 長さ:\(\alpha\)の長さが、\(\frac{1}{\betaの長さ\ \ \ }\)倍された。
- 偏角:\(\alpha\)の偏角から、\(\beta\)の偏角だけ逆回転した。
よって、次のことがわかります。
ポイント
2つの複素数\(\alpha,\beta\)について、商\(\frac{\alpha}{\beta}\)は
- \(\alpha\)の長さを、\(\frac{1}{\betaの長さ\ \ \ }\)倍する
- \(\alpha\)の偏角から、\(\beta\)の偏角だけ逆回転する
まとめ


まとめ
- 複素数\(a+bi\)は、ベクトル\(\begin{pmatrix}a\\ b\\ \end{pmatrix}\)を描く。
- 複素数の和・差・実数倍はベクトルと一致させて考えれば良い。
- 複素数の積は、極形式に着目して距離倍、偏角だけ回転させれば良い。
- 複素数の商は、複素数の積に帰着して考えれば良い。\(\frac{1}{距離倍}\)、逆回転する。
高校の複素平面は、ほんの触り。
大学数学に入ってから学ぶ複素解析の導入でしかありません。
逆に言えばこの図形的なイメージさえあれば、なんとか乗り切れます。まずはここから。
以上、「複素数の計算と、図形的なイメージについて」でした。おつかれちゃん。
Q. 点\(A(3+i)\)を、原点中心に\(-\frac{\pi}{2}\)だけ回転させた点\(B(\beta)\)を求めよ。
複素数を、\(-\frac{\pi}{2}\)だけ回転させるためには、
\(\cos \left(-\frac{\pi}{2}\right)+i\sin\left(-\frac{\pi}{2}\right)\)
をかけてあげれば良い。よって、
\begin{align} \beta &= (3+i)\left(\cos \left(-\frac{\pi}{2}\right)+i\sin\left(-\frac{\pi}{2}\right)\right)\\\ &= (3+i)(0-i)\\\ &= 1-3i\\\ \end{align}









