Today's Topic
・極形式は原点からの距離と、偏角に着目して複素数を表現したもの
・複素数\(x+yi\)を極形式に表すためには、
- 原点からの距離に着目して、\(r=\sqrt{x^2+y^2}\)を求める。
- \(r\)でくくって、\(r(\frac{x}{r}+\frac{y}{r}i)\)を作る。
- \(\cos\theta=\frac{x}{r},\sin\theta=\frac{y}{r}\)を満たす\(\theta\)を求める。
のようにすれば良い。
・複素数の指数を考える、あるいは図を考えるためには、極形式にして考えれば良い。




この記事を読むと、この意味がわかる!
- 複素数\(1+i\)を極形式に直せ。
- 複素数\(1+i\)は、実軸から何度回転した点か。

複素数を一気に理解したい方への記事は、こちらにまとめてあります。
Contents
極形式とは |極形式にしたくなるキモチ
通常、複素数\(x+yi\)を考えるとき、意識されているイメージは次のような動きです。
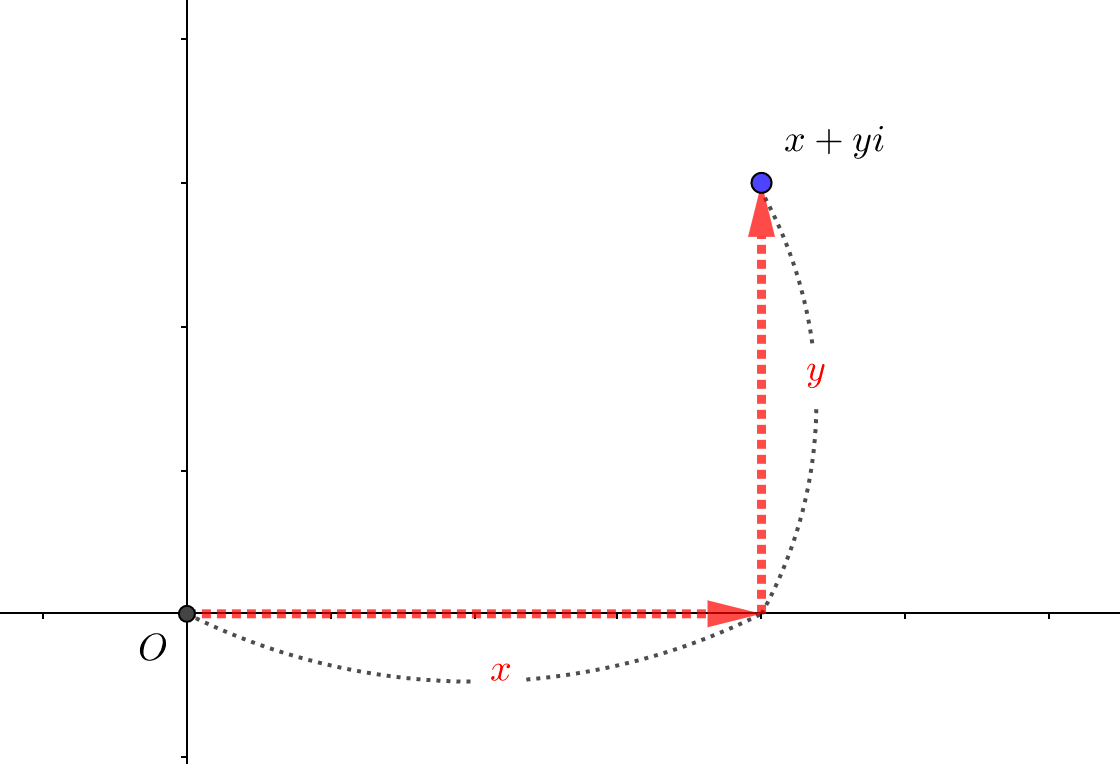

- 実部:横にどれだけ進んだか
- 虚部:縦にどれだけ進んだか
一方で極形式は目線を変えて、『原点からの距離とどれだけ回転したか』に着目して、複素数を表した式です。
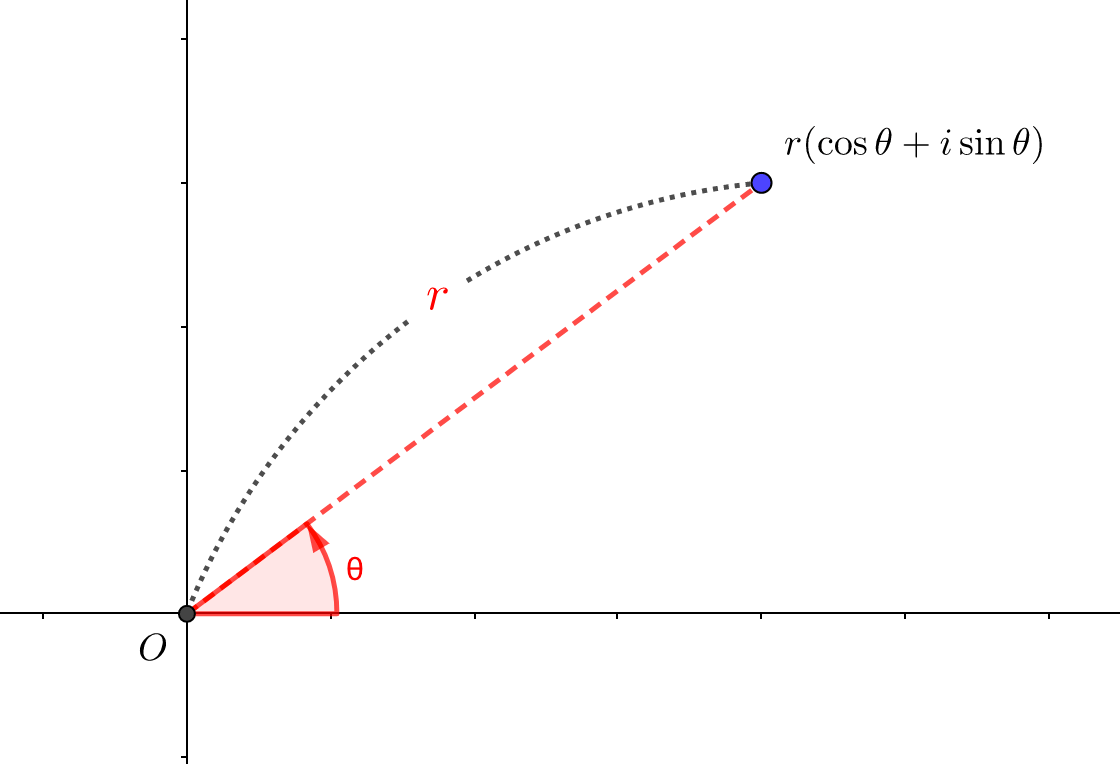

- r:原点からどれだけの距離があるか
- \(\theta\):実軸からどれだけ回転したか
同じ点について表しているのですが、表し方は2通りあるということですね。
ちなみに\(\theta\)のように、ある点がどれだけ回転したかを表す角度を偏角と言います。




極形式に変形するコツ
ここでは、複素数を極形式の形にする手順をご紹介します。
先ほどの図とも絡めて、各変形にどのようなイメージが込められているのかを見ていきましょう。
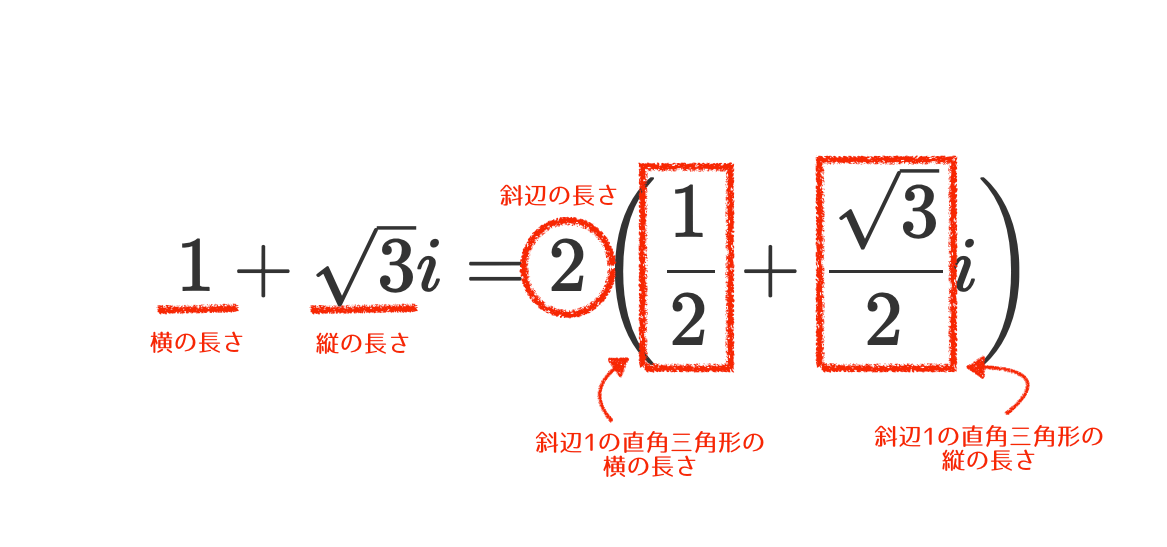
具体的に\(1+\sqrt{3}i\)を極形式にしていく手順を見ていきましょう。
step
1rを求める
まずは、実数\(r\)を求めるところから始めましょう。
\(r\)は次の式で求めることができます。
ポイント
複素数\(x+yi\)の原点からの距離\(r\)は
$$r=\sqrt{x^2+y^2}$$
で求められる。


\(r\)は原点からの距離を表していたので、三平方の定理を意識しています。
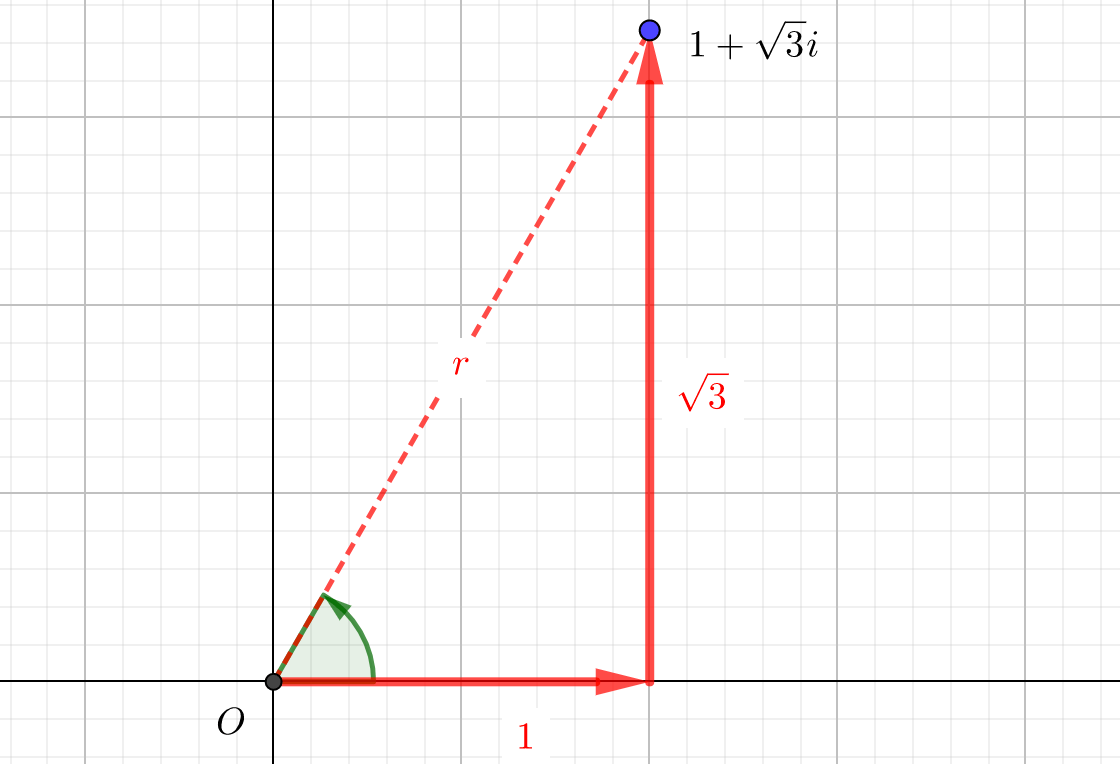

よって\(r=2\)
step
2\(\theta\)を求める
距離\(r\)を求めたら、複素数を\(r\)でくくってあげます。
このカッコの中に注目します。
ここで極形式の一般形と見比べてみてください。
$$r\left(\color{red}{\cos\theta}+i\color{blue}{\sin\theta}\right)$$
- \(\cos\theta=\frac{1}{2}\)
- \(\sin\theta = \frac{\sqrt{3}}{2}\)
という関係になっているのがわかります。
これを満たす\(\theta\)は
がありますね。
ここで注意してもらいたいのは、極形式の表し方は別に一通りとは限らないということです。
他にも\(\frac{7}{3}\pi\)など、たくさんあります。
このような理由で、問題文には基本的に\(\theta\)の範囲が与えられます。
仮に範囲がないとすると、
のように表すのが最適でしょう。


極形式に変形するコツ|変形過程のキモチ
ここでは極形式に変形する際、なぜそのように変形したのかを考えていきます。
ここで重要になるのが、サインコサイン の定義です。
サインコサイン について復習したい人はこちらを参考にしてください。
続きを見る



【中学生でもわかった】サインコサインとは?公式を暗記しなくても、感覚でわかる!
サインとコサインはそもそも、斜辺が1の直角三角形の高さと底辺として、定義されています。
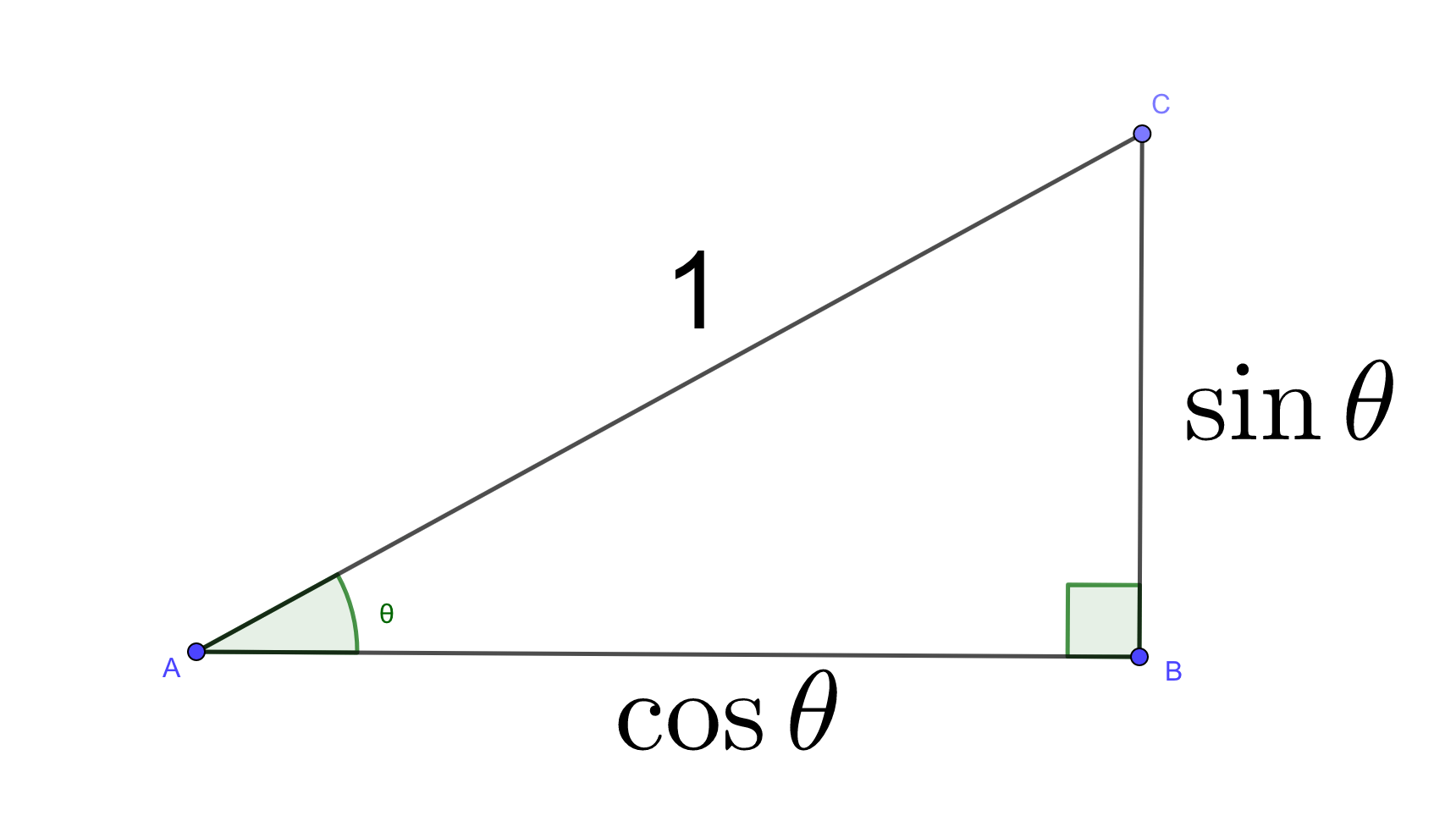
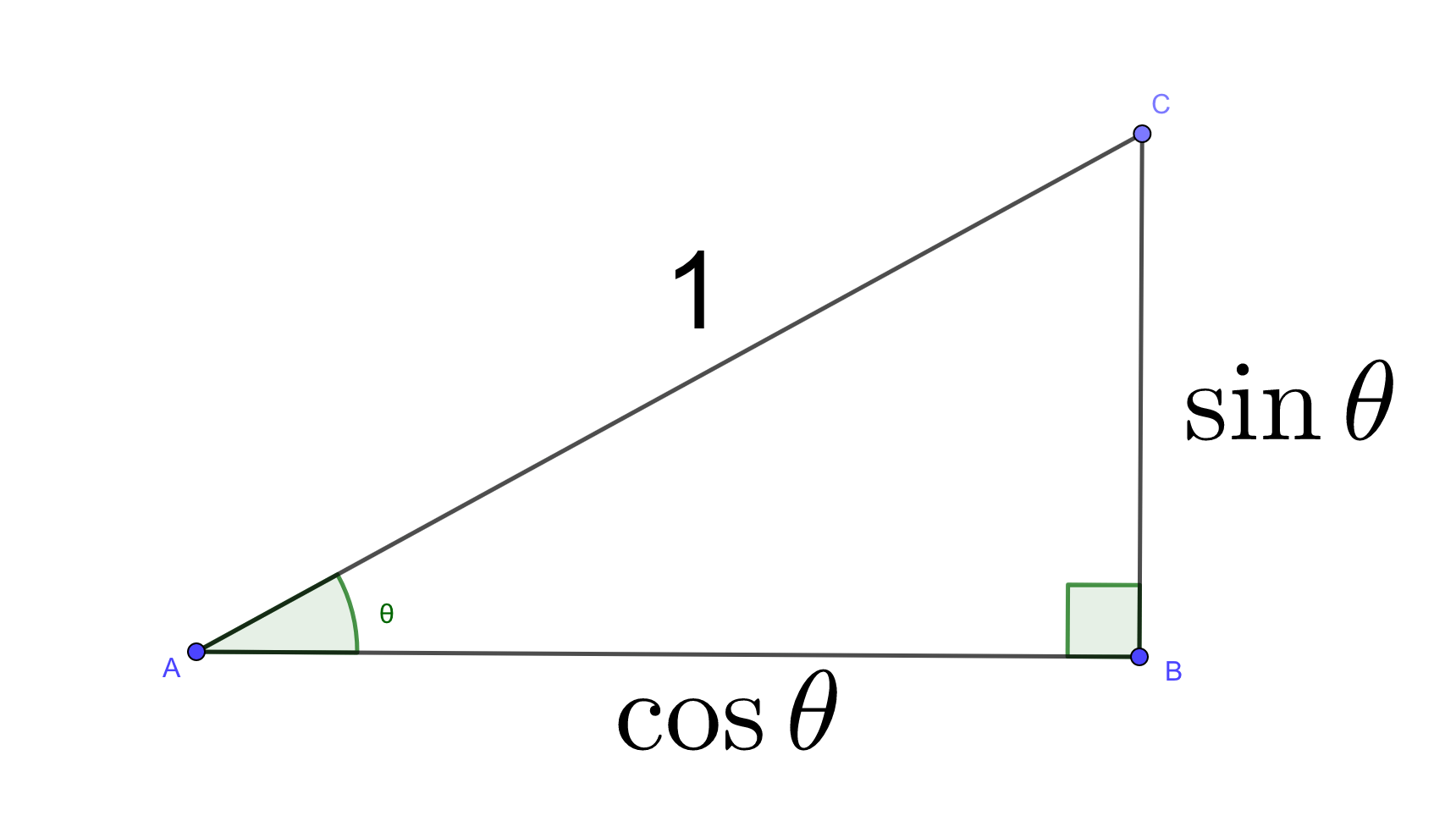
もし斜辺の長さが\(r\)の場合、すべての辺を\(r\)倍することで三角形の形はそのままで大きさだけが変わります(相似)。
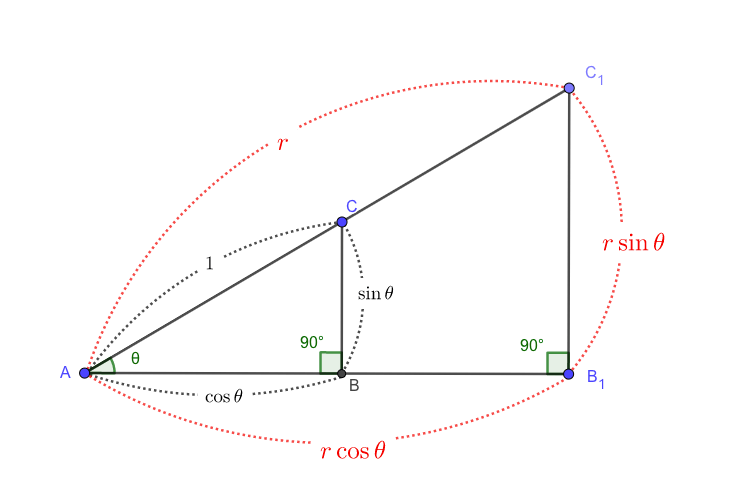



極形式に変形する際、まず最初に距離\(r\)の長さを求めました。
これは斜辺1の直角三角形が何倍されたのか、を調べるためです。
そしてStep2の\(r\)でくくったカッコの中に注目したのは、斜辺が1の直角三角形について考えているのです。



結局、極形式は表し方が違うみたいな話をしましたが、考えていることは
横にいくつ、縦にいくつ進んだか
に過ぎません。
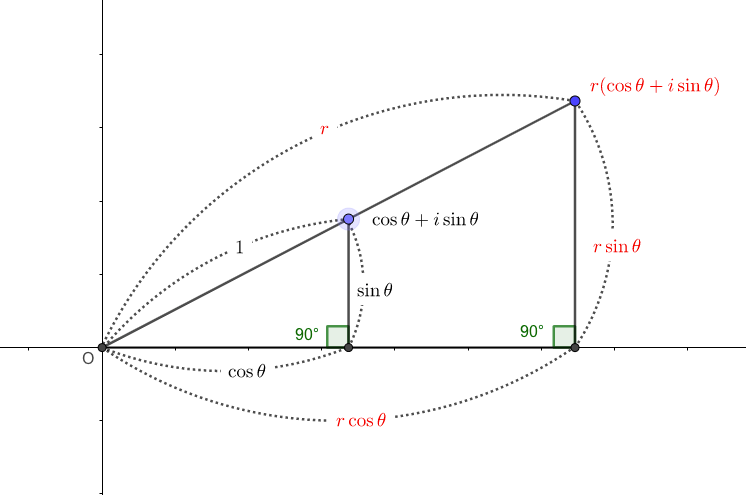

図を見てもらえば分かる通り、
- 横:\(x\rightarrow r\cos\theta\)
- 縦:\(y\rightarrow r\sin\theta\)
のように、表し方を変えただけとなっています。


極形式に表すメリット
では最後に極形式にするタイミング、したほうがいいタイミングについて考えていきましょう。
複素平面上での動きが見える
まず複素数の形と、極形式の形を見比べてみます。
すると圧倒的に極形式の方が斜辺の長さや角度がわかりやすい構造になっています。
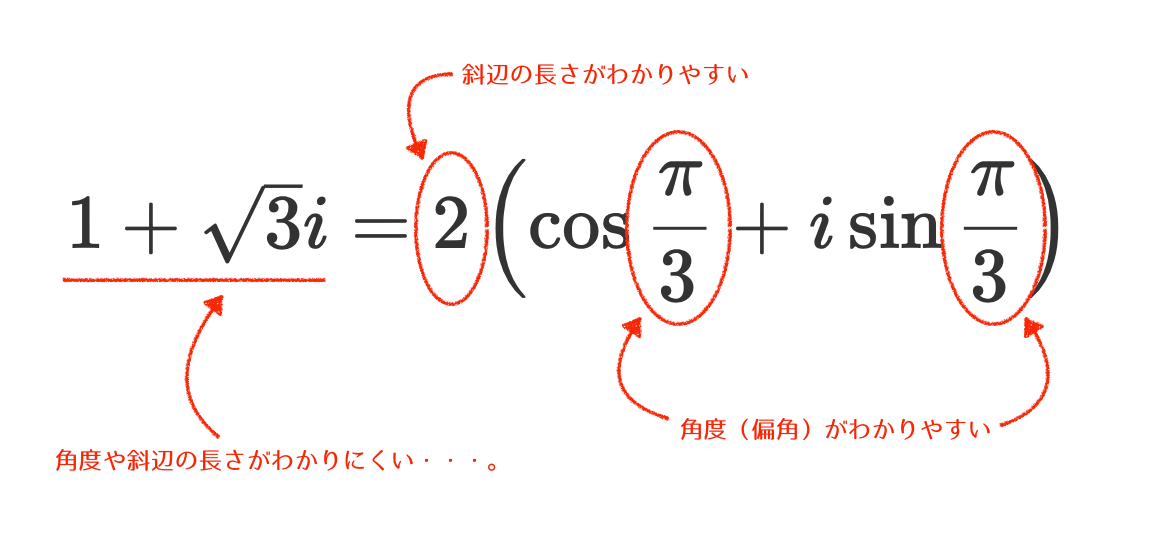
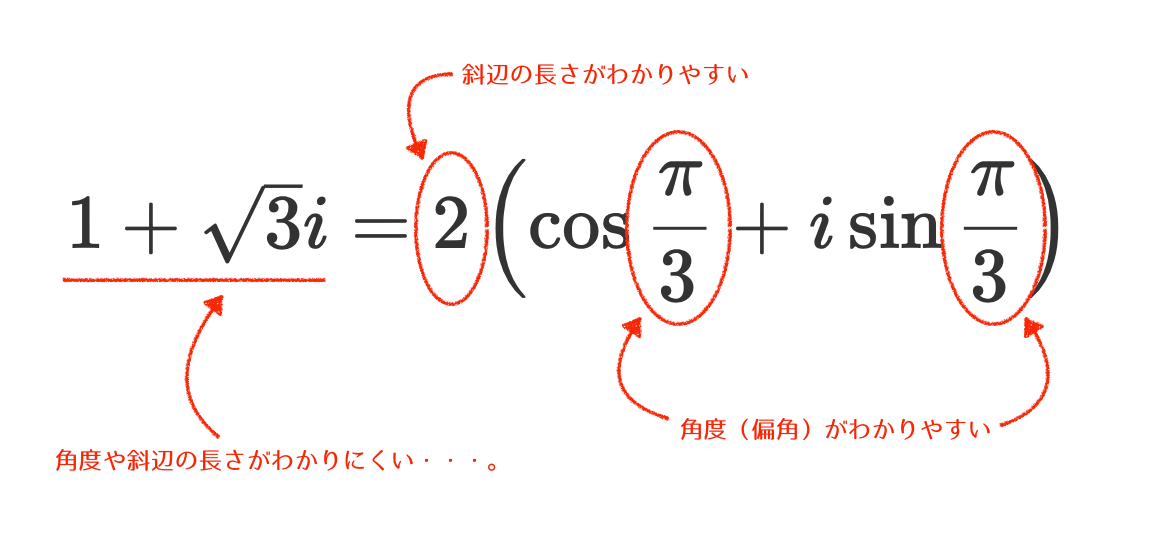
ですが、極形式の形はサインコサインがいるため、計算が非常にめんどくさいというデメリットもあります。
そこで大まかな使い分けとしては、
ポイント
- 複素数の形→計算するとき
- 極形式の形→図を考えるとき
と考えるといいのではないでしょうか。
複素数の〜乗が考えられる
複素数はこれまで扱ってきた実数とは、少し雰囲気が異なる数です。
中でも複素数の指数法則は、特殊な印象を受けると思います。
\((1+\sqrt{3}i)^2\)など、指数が簡単であればそのまま計算すればいいでしょう。
では\((1+\sqrt{3}i)^{10}\)のように、指数が大きい場合はどうすればいいのでしょうか。
このときに活躍するのが、ド・モアブルの定理と呼ばれるものです。
ド・モアブルの定理
どんな整数\(n\)でも
$$\left(\cos\theta+i\sin\theta\right)^n=\cos n\theta+i\sin n\theta$$
が成り立つ。
ドモアブルの定理について復習したい人はこちらを参考にしてください。
続きを見る



ド・モアブルの定理の証明と問題場面→極形式の形に直せればOK
ド・モアブルの定理は、複素数の指数を考える最強のツール。
が、定理を見て分かる通り極形式に表して初めて使えるツールとなっています。
つまり複素数の指数を考える上では、極形式は必須の表現方法ということになります。
まとめ


まとめ
・極形式は原点からの距離と、偏角に着目して複素数を表現したもの
・複素数\(x+yi\)を極形式に表すためには、
- 原点からの距離に着目して、\(r=\sqrt{x^2+y^2}\)を求める。
- \(r\)でくくって、\(r(\frac{x}{r}+\frac{y}{r}i)\)を作る。
- \(\cos\theta=\frac{x}{r},\sin\theta=\frac{y}{r}\)を満たす\(\theta\)を求める。
のようにすれば良い。
・複素数の指数を考える、あるいは図を考えるためには、極形式にして考えれば良い。
極形式に変形する過程は練習すればササッとできるようになるので、それほど心配する必要はありません。
問題は極形式に変形するシーンを見抜けるかどうかです。
ある程度計算して、ここで極形式に変形すれば一番楽だなというタイミングが見極められれば最高です。
是非いろんな問題に触れて、変形するベストなタイミングを見つけてください。
以上、「極形式に表すメリットとコツ」についてでした。
チェック問題
例題
複素数\(1+i\)を極形式に直せ。
まず原点からの距離rを求める。
次に、rで式をくくる。
最後に
$$\sin\theta=\frac{1}{\sqrt{2}}$$
を満たす\(\theta\)を求める。


以上より、
ではなく、




例題
複素数\(1+i\)は、実軸から何度回転した点か。
極形式に直すと
だった。
よって45度。









