共役な複素数の重要性質４つ→特殊計算・分割可能・方程式の解・複素平面

Today's Topic

『複素数$a+bi$に対して、$a-bi$で表せる複素数を、共役な複素数という。』

楓

今日は共役な複素数について、解説するよ〜！

共役な複素数って、パッと扱っちゃダメなテーマなの？そこまで難しくないけど・・・？

小春

楓

共役な複素数には、複素数の問題を解く上で絶対外せない性質がいくつかあるんだ。今回はその性質にフォーカスしていくよ！

こんなあなたへ

「共役な複素数って、何か特別なの？」

「共役な複素数の性質や使い方が知りたい！」

この記事を読むと、この意味がわかる！

ある二次方程式の解が、$x=3+2i$であった。このときのもう１つの解を求めよ。
$z+\frac{1}{z}$が純虚数ならば、複素数$z(z\neq0)$も純虚数であることを示せ。

答えは一番最後にあるよ！

楓

複素数を一気に理解したい方への記事は、こちらにまとめてあります。

まとめ記事

: 【複素数公式一覧】証明や差がつくポイント、役立つテクニックなど総まとめ（数Ⅱ・数Ⅲ対応）

続きを見る

Contents

1 共役（きょうやく）な複素数とは
2 共役な複素数による重要性質4つ
3 まとめ

共役（きょうやく）な複素数とは

定義

複素数$a+bi$に対して、$a-bi$のように虚部を$-1$倍した関係にある複素数のこと。

例えばこんな感じ。

$$1+2i \rightarrow 1-2i$$
$$3-i \rightarrow 3+i$$
$$\sqrt{2}i \rightarrow -\sqrt{2}i$$
$$5 \rightarrow 5$$

小春

$\sqrt{2}i$や5のような実数や純虚数は、複素数$a+0i$や$0+bi$の場合だと見なせばいいね。

共役な複素数による重要性質4つ

ここからは共役な複素数が見せる、とても便利な性質をご紹介していきます。

共役な複素数を足す/掛けると実数化する

複素数$a+bi$に対して、共役な複素数を足してみます。

\begin{align} (a+bi)+(a-bi) &= (a+a)+(b-b)i\\\ &= 2a\\\ \end{align}

（※見切れている場合はスクロール）

ご覧の通り、虚部が相殺して実部が2倍された数のみ残りました。

楓

式からもわかるけど、引き算の場合は逆に虚部だけが残るね。

\begin{align} (a+bi)-(a-bi) &= (a-a)+(b+b)i\\\ &= 2bi\\\ \end{align}

（※見切れている場合はスクロール）

次に、共役な複素数を掛けてみましょう。

\begin{align} (a+bi)(a-bi) &= \left(a^2+b^2\right) +(-ab+ab)i\\\ &= a^2+b^2\\\ \end{align}

（※見切れている場合はスクロール）

こちらもまた、虚部が相殺して実数のみになりました。

出来上がった実数$a^2+b^2$は、必ず正の値しかとらないことも大切です。

共役な複素数は分割できる

複素数$z$に対して、共役な複素数を$\overline{z}$と表します。

このとき、２つの複素数$\alpha,\beta$について、以下２つの性質が成り立ちます。

$$\overline{\alpha\pm\beta}=\overline{\alpha}\pm\overline{\beta}$$
$$\overline{\alpha\beta}=\overline{\alpha}\cdot\overline{\beta}$$

小春

割り算のときは、いつも通り掛け算のときに帰着して考えればいいのね。

証明は右辺と左辺が等しい値になることを言えばOK！

楓

また、$\overline{\alpha\beta}=\overline{\alpha}\cdot\overline{\beta}$より

$$\overline{\alpha^n}=\left(\overline{\alpha}\right)^n$$
$$\overline{k\alpha}=k\overline{\alpha}(kは実数)$$

ということもできます。

小春

共役な複素数を表す上バーが分割できるってみなせるね。

$a+bi$が（実数係数の）方程式の解になるとき、共役複素数$a-bi$も解

方程式の解に$1+i$が含まれるとき、$1-i$も必ず解になっているという、一度で2度美味しい性質です。

いきなりこの証明に取り掛かるのは厳しいので、まずは実験をしてみましょう。

二次方程式$x^2+2x+3=0$を考えてみると、解の公式から

\begin{align} x &= \frac{-2\pm\sqrt{4-12}}{2}\\\ &= -1\pm\sqrt{2}i\\\ \end{align}

となります。

楓

確かに共役な複素数も解になったね。

では三次方程式$x^3=1$を考えてみましょう。

$x=1$は解になるので、$x^3-1=0$は$(x-1)$で因数分解できるはずです。

整式の割り算等を駆使して、

$$x^3-1=(x-1)(-x^2-x-1)$$

のように因数分解します。

すると$-x^2-x-1=0$を考えればよく、二次方程式に落とし込むことができます。

解の公式から

\begin{align} x &= \frac{-1\pm\sqrt{1^2-4}}{2}\\\ &= -\frac{1}{2}\pm\frac{\sqrt{3}i}{2}\\\ \end{align}

となり、これも共役複素数が答えになっていることが確認できました。

ではここから、一般的に$n$次方程式の証明をしてみましょう。

$n$次方程式

$$f(x)=k_0+k_1x+k_2x^2+\cdots=0(k_0,k_1,\cdotsは実数)$$

（※見切れている場合はスクロール）

が虚数解$z=a+bi$を持つと仮定します。

ここから$\overline{z}=a-bi$が解として求められることを示せばOKですね。

楓

整式の性質から、$f(z)=0$が成り立つことに注目しておこう。

step
1整式$f(\overline{z})$を$f(z)$に帰着させる。

$n$次方程式$\overline{f(z)}$について考える。

上記で既に説明した共役複素数の性質$\overline{\alpha\pm\beta}=\overline{\alpha}\pm\overline{\beta}$より

\begin{align} \overline{f(z)} &= \overline{k_0+k_1z+k_2z^2+\cdots} \\\ &= \overline{k_0}+\overline{k_1z}+\overline{k_2z^2}+\cdots\\\ \end{align}

と変形できる。

さらに、共役複素数の性質

$\overline{k\alpha}=k\overline{\alpha}(kは実数)$
$\overline{\alpha^n}=\left(\overline{\alpha}\right)^n$

を順に使うことにより、

\begin{align} \overline{k_0}+\overline{k_1z}+\overline{k_2z^2}+\cdots &= k_0+k_1\overline{z}+k_2\overline{z^2}+\cdots\\\ &= k_0+k_1\overline{z}+k_2\left(\overline{z}\right)^2+k_3\left(\overline{z}\right)^3\cdots\\\ \end{align}

（※見切れている場合はスクロール）

となり、これは$f(\overline{z})$を表す。

よって$\overline{f(z)}=f\left(\overline{z}\right)$が言える。

step
2実数の共役複素数は、そのまま

問題の条件から、$f(z)=0$が成り立つのだった。

楓

さっき注目してねって言ったところだよ！

実数$0$は複素数$0+0i$と一致するので、0の共役複素数は$0-0i=0$となる。

ゆえに$f(z)=0$ならば、$\overline{f(z)}=\overline{0}=0$となる。

step
3Step1、2を連結

Step1より、$\overline{f(z)}=f\left(\overline{z}\right)$
Step2より、$\overline{f(z)}=\overline{0}=0$

繋げると、

$\overline{f(z)}=0$ならば、$f\left(\overline{z}\right)=0$

となる。

よって$n$次方程式が複素数を解に持つとき、その共役複素数も解になることが示された。

お疲れちゃん。

数Ⅲ複素平面上で$x$軸対称の位置にいる

複素平面上で２つの複素数$1+1i$、$-3+2i$とその共役複素数をプロットすると、図のような位置関係にいます。

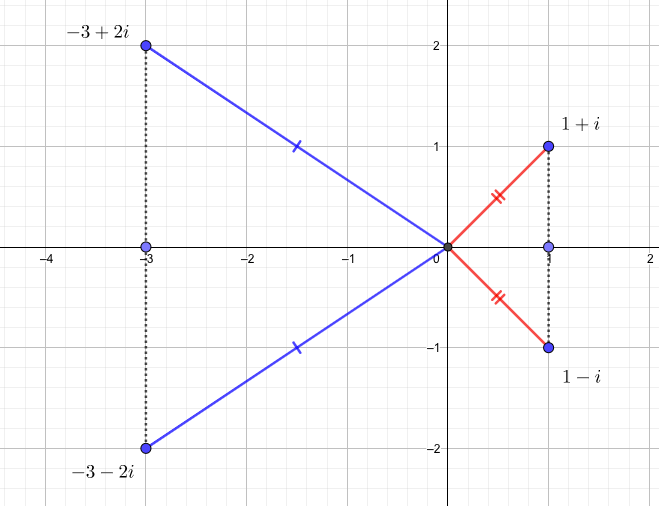
この図から、複素数$z$と共役な複素数$\overline{z}$には次のような関係があると言えます。

$x$軸対称
原点からの距離が等しい

特に後者の性質から、$z=a+bi$とすると、

原点から複素数$z$までの距離を|z|とするとき、
$$|z|=|\overline{z}|=\sqrt{a^2+b^2}$$

と言えます。

小春

複素数と、その共役な複素数は距離が変わらないんだね。

これは、最初らへんに述べた

『複素数とその共役複素数の積は、非負実数$a^2+b^2$になる』

という感覚とも一致しますね。

まとめ

楓

長くなったね、まとめておきましょう。

まとめ

複素数$z=a+bi$と、その共役な複素数$\overline{z}=a-bi$について

$z+\overline{z}=2a$
$z\overline{z}=|z|^2=a^2+b^2$
$|z|=|\overline{z}|$
方程式の解が$z$のとき、$\overline{z}$も解

２つの複素数$\alpha,\beta$について

$\overline{\alpha\pm\beta}=\overline{\alpha}\pm\overline{\beta}$
$\overline{\alpha\beta}=\overline{\alpha}\overline{\beta}$
$\overline{\alpha^n}=\left(\overline{\alpha}\right)^n$
$\overline{k\alpha}=k\overline{\alpha}$

小春

合わせて８つもあるの？！

そうだけど、暗記するのではなく理解すれば簡単だよ。

楓

共役複素数を持つ複素数の世界では、感覚的にはちょっと不思議な、でも成り立つとありがたい性質がこんなにもあります。

これから先、複素数の問題を解いていけばわかりますが、この特殊な性質を使わない問題はまずありません。

この性質を完璧に理解して、自分のものにすることで、複素数はちゃんと得点源になりますよ。

以上、「共役複素数について」でした。

最初の答え
Q.ある二次方程式の解が、$x=3+2i$であった。このときのもう１つの解を求めよ。

複素数が方程式の解となるとき、共役複素数もまた解になる。

よって$x=3+2i,3-2i$を解に持つ。

Q.$z+\frac{1}{z}$が純虚数ならば、複素数$z(z\neq0)$も純虚数であることを示せ。

複素数と共役複素数の和は、虚部が相殺して実数になる。

これより純虚数とその共役複素数の和は0になるはずである。

よって、

$$\left(z+\frac{1}{z}\right)+\overline{\left(z+\frac{1}{z}\right)}=0$$

整理すると、

$$(z+\overline{z})+\frac{\overline{z}+z}{z\overline{z}}=0$$

となる。

$z\overline{z}=|z|^2$に注意して$(z+\overline{z})$でくくると、

$$(z+\overline{z})\left(1+\frac{1}{|z|^2}\right)=0$$

$\left(1+\frac{1}{|z|^2}\right)>0$より、$(z+\overline{z})=0$

これが成り立つとき、実部は0のはずである。よって$z$は純虚数。

共役な複素数の重要性質４つ→特殊計算・分割可能・方程式の解・複素平面

【複素数公式一覧】証明や差がつくポイント、役立つテクニックなど総まとめ（数Ⅱ・数Ⅲ対応）

共役（きょうやく）な複素数とは

共役な複素数による重要性質4つ

共役な複素数を足す/掛けると実数化する

共役な複素数は分割できる

\(a+bi\)が（実数係数の）方程式の解になるとき、共役複素数\(a-bi\)も解

数Ⅲ複素平面上で\(x\)軸対称の位置にいる

まとめ

【微分公式一覧】証明や差がつくポイント、役立つテクニックなど総まとめ

【感覚で理解できる！】常用対数とは？意味と使い方を徹底解説！！

自然対数、ネイピア数とは？なぜあの定義なのか、何が自然なのか。お金の話で超簡単に理解できる！！

【指数関数の定義】なぜ底が負のときは定義しないのか→ダルいから

【整数の指数法則】なぜ0乗が1なのか、息をするようにわかる指数法則