【単調増加・単調減少】って、結局どう使えばいいのでしょうか？→不等式やグラフで活用しよう！

楓

今日は数学の中でも、かなり重要な「単調増加・減少」について扱うよ！

どういうことに使われるんだろう？

小春

楓

活用場面で多いのは証明。単調増加であることを示せれば、かなり有利になるよ！

じゃあ今日はその使い方と意味まで教えて欲しいな！

小春

単調増加・単調減少の定義

楓

まずはじめに定義から確認してみよう。

これは単調増加をしているグラフを実際に見ながら考えると、理解がしやすくなります。

単調増加しているグラフの例

小春

なるほど、要は\(f(x)\)はその手前の値よりも常に大きくなるってことね！

おお、いいこと言う！単調減少はその逆で、手前の値よりも常に小さい値をとるってことだね！

楓

単調増加・単調減少かどうかの判定方法

定義自体はカンタンですが、単調増加・単調減少であることを示そうと思うと定義だけでは難しいです。

そこで導関数の考え方を使い、以下のように判定します。

導関数で判定できる理由

微分係数の定義の中で、

と紹介しました。

導関数は微分係数を一般的に求めるための関数であり、導関数が0以上であれば、その関数のどの点で接線を引いても傾きは0以上になることを意味します。

そして、その接線の傾きには、次のような性質があることはグラフを見て明らかでしょう。

接線の傾きが負の方向に大きくなる→グラフが落ち込む

 

接線の傾きが正の方向に大きくなる→グラフが持ち上がる

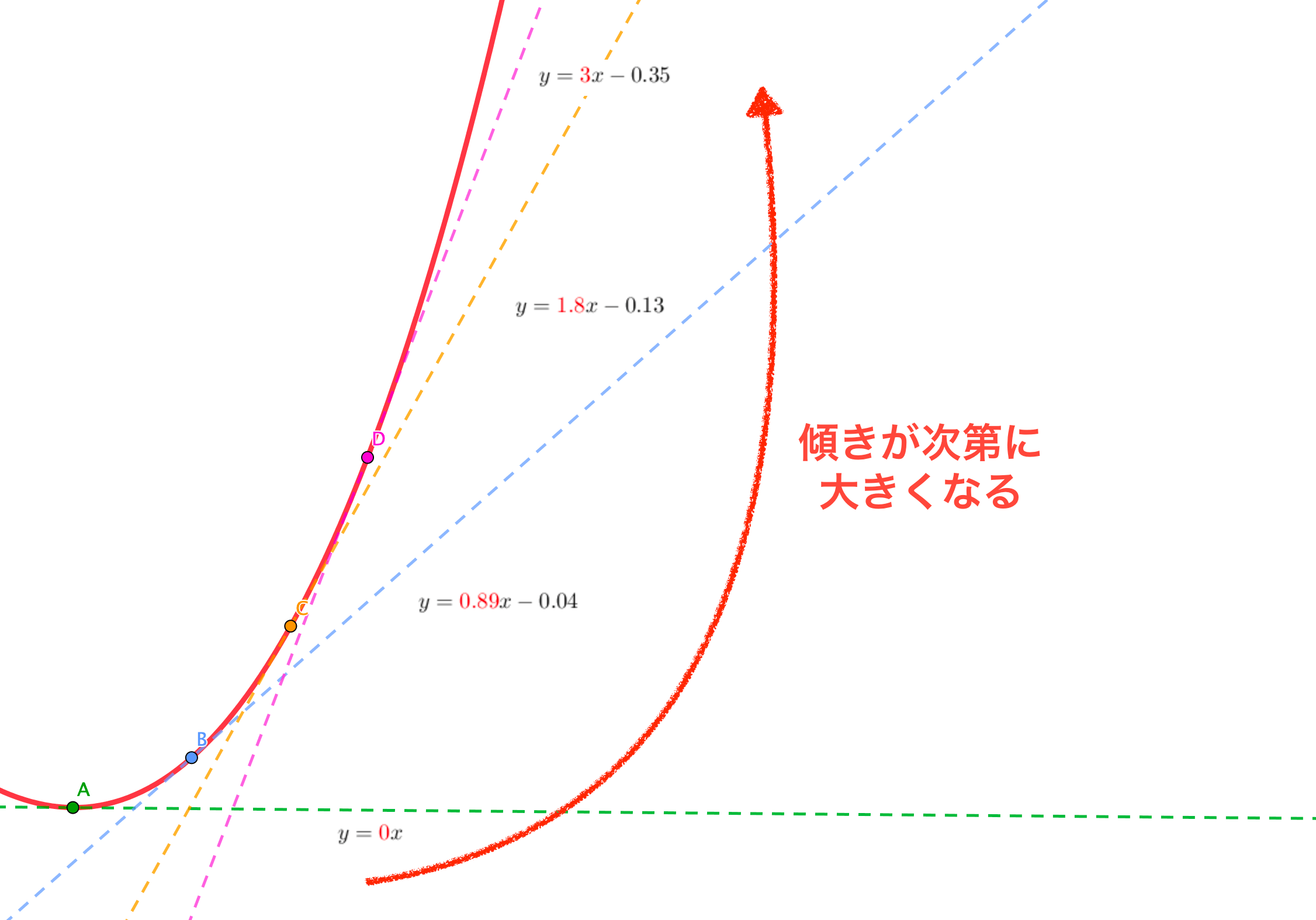
つまり「導関数が常に正である」とは、どの場所で接線を引いても傾きが正ということを表しているので、グラフが落ち込むことなく持ち上がり続けるということを意味します。

これは単調増加の意味していることそのものですね。

ここではあえて直感的で、ちょっと曖昧な証明に留めました。

実はこの証明には平均値の定理と呼ばれるものを使います。

下記記事の例題で紹介してますので、気になる人は見てみましょう。

単調増加・単調減少を使う場面

単調増加・単調減少は特定の問題で大活躍します。

それらの問題に共通するのは、『単調増加・単調減少の性質を使わないと証明できない』ということ。

それでは、よく使われる考え方を見ていきましょう。

グラフの形に見当をつけられる

グラフを見ることで、単調増加・単調減少への理解がしやすくなりましたね。

これは逆も同じで、単調増加・単調減少であることがわかると、グラフの形が容易に想像できます。

例えば、単調増加であるとわかっているグラフは\(y\)座標の値が常に手前の値よりも大きくなりました。

これはつまり、グラフの形で言えば「凹むことがない」ということです。

もしあなたが問題を見て、下書きでこのようなグラフを描いていたとしましょう。

 

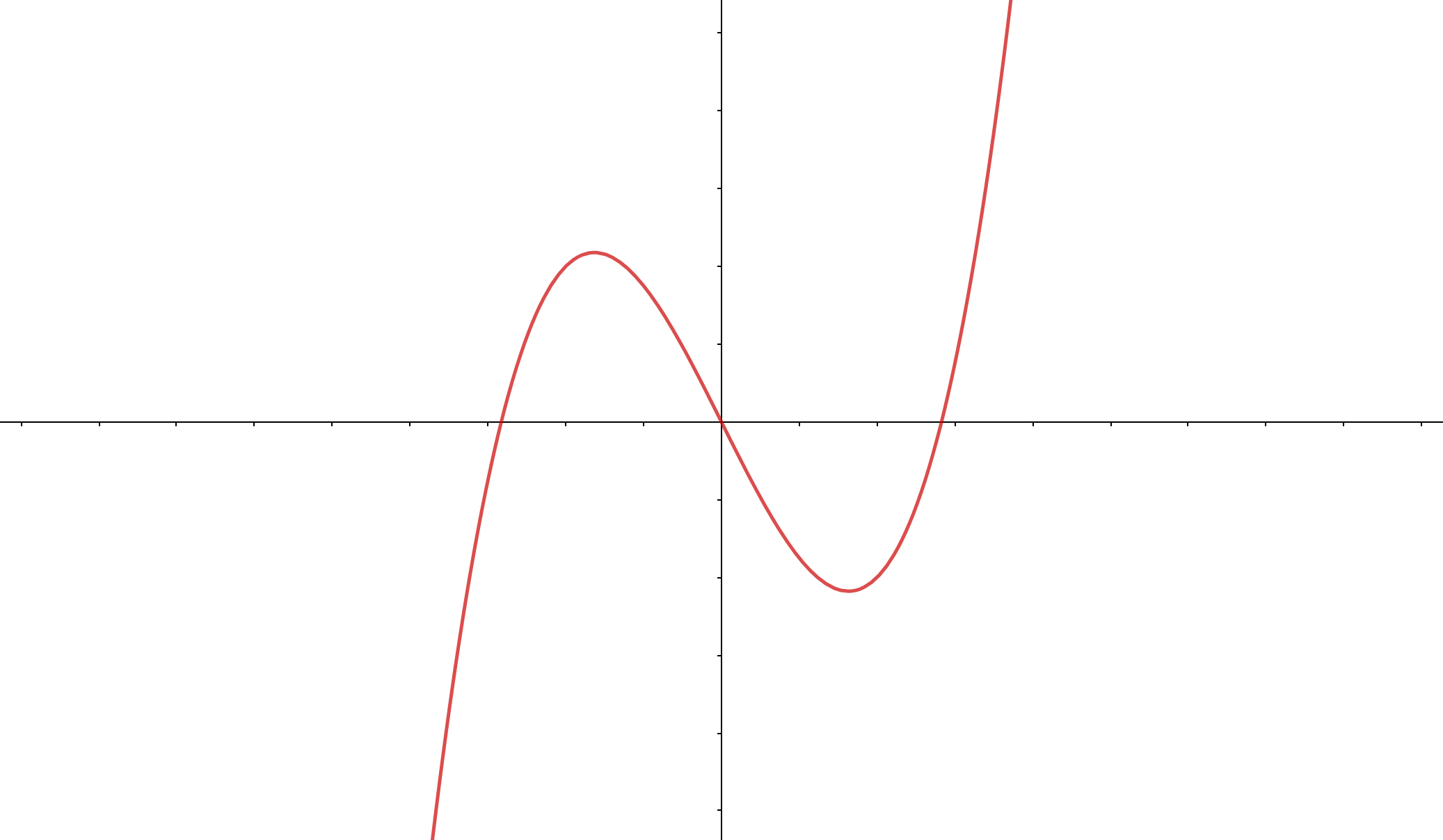
しかし解答している間に、単調増加であることがわかれば次のような形だと予想できます。

小春

そうか、凹むってことは「減る→0→増える」か、「増える→0→減る」のどちらかが起きているってことだもんね！

その通り、単調に増加するためにはずっと増え続けなきゃいけないし、単調減少だと減り続けなきゃいけないよ！

楓

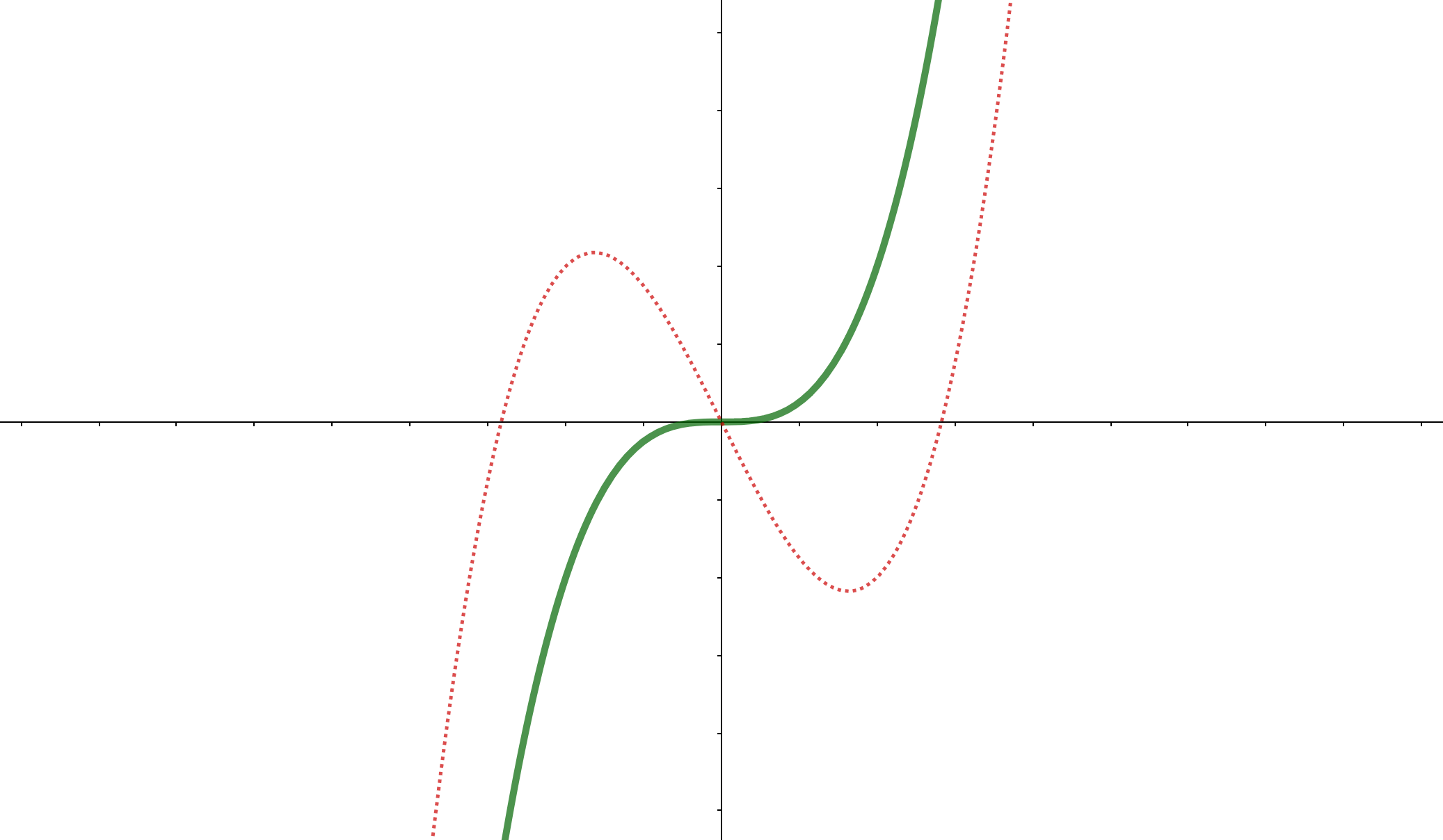
不等式問題へのアプローチになる

これは次の例題を参考にした方がわかりやすいでしょう。

をもとに、不等式を証明することができました。

これはよく使われる手法なので、必ずマスターしておきましょう。

楓

難しい不等式を見たら、単調増加・単調減少が使えないか試してみよう！

まとめ

楓

最後にまとめてみましょう！

今回は単調増加・減少について扱いました。

定義自体はそれほど難しくないため、有用性がイマイチわかりにくいかもしれませんが、多くの問題でキーポイントになる重要な考え方です。

もっともベストな理解の仕方は、いろんな問題を解いて単調増加・単調減少がどのようなアプローチで使われているか経験することだと思います。

もう一度言いますが、絶対マスターしましょう。

以上、「単調増加・単調減少について」でした。