Today's Topic
媒介変数表示されたグラフを描くためには、
- \(\frac{dx}{dt},\frac{dy}{dt},\frac{dy}{dx}\)を求め、
- \(\frac{dx}{dt}=0,\frac{dy}{dt}=0\)となる\(t\)の値を求め、
- それを元に増減表を描き、グラフで大まかな点を打つ。
- 最後にその2点間のカーブの仕方を極限で調べればOK!

例題
$$\left\{ \begin{array}{l} x=\cos^3 t \\ y=\sin^3 t \end{array} \right. \ (0≦t≦\pi)$$
のグラフを描け。

この記事を読むと、この意味がわかる!
- 媒介変数表示されたグラフを、効率的に解く方法
- 2階微分の不必要性と、媒介変数の本質

媒介変数表示の2階微分がしんどい
さて、まずグラフを描くといって一番最初に思い浮かぶのは微分です。
媒介変数表示の場合、導関数\(\frac{dy}{dx}\)を求めるところから始めます。
\(\frac{dx}{dt}=-3\cos^2 t\sin t, \ \frac{dy}{dt}=3\cos t \sin^2 t\)
媒介変数の微分法を用いて、
$$\frac{dy}{dx} = \frac{\frac{dy}{dt}}{\frac{dx}{dt}} = -\tan t$$
となりますが、2階微分\(\frac{d^2y}{dx^2}\)の値を求めるためには、少し工夫が必要になります。

この2階微分が一筋縄では行かないワケで、2階微分の値は次のようになります。

符号の変化さえ、わかればいい
ここで、ちょっと立ち止まって考えてみましょう。
これまで凹凸のあるグラフを描くとき、必ず2階微分を調べてきましたが、そもそも何が知りたくて計算していたのでしょうか?
それは、『2階微分の符号の変化』を知りたかったから。

要は2階微分しなくても、2階微分した値の正負さえ、わかればいいのです。
2階微分をもう一度考えてみると、
なので、2階微分の符号は\(\frac{dy}{dt},\frac{dx}{dt}\)に依存していることがわかります。

\(\frac{dx}{dt}=0,\frac{dy}{dt}=0\)のとき、\(t=0,\frac{\pi}{2},\pi\)
ここまでで、増減表は次のようになる。
| $$t$$ | $$0$$ | $$\cdots$$ | $$\frac{\pi}{2}$$ | $$\cdots$$ | $$\pi$$ |
| $$\frac{dx}{dt}$$ | $$0$$ | $$-$$ | $$0$$ | $$-$$ | $$0$$ |
| $$x$$ | $$1$$ | $$\searrow$$ | $$0$$ | $$\searrow$$ | $$-1$$ |
| $$\frac{dy}{dt}$$ | $$0$$ | $$+$$ | $$0$$ | $$-$$ | $$0$$ |
| $$y$$ | $$0$$ | $$\nearrow$$ | $$1$$ | $$\searrow$$ | $$0$$ |
| $$(x,y)$$ | $$(1,0)$$ | $$(0,1)$$ | $$(-1,0)$$ |

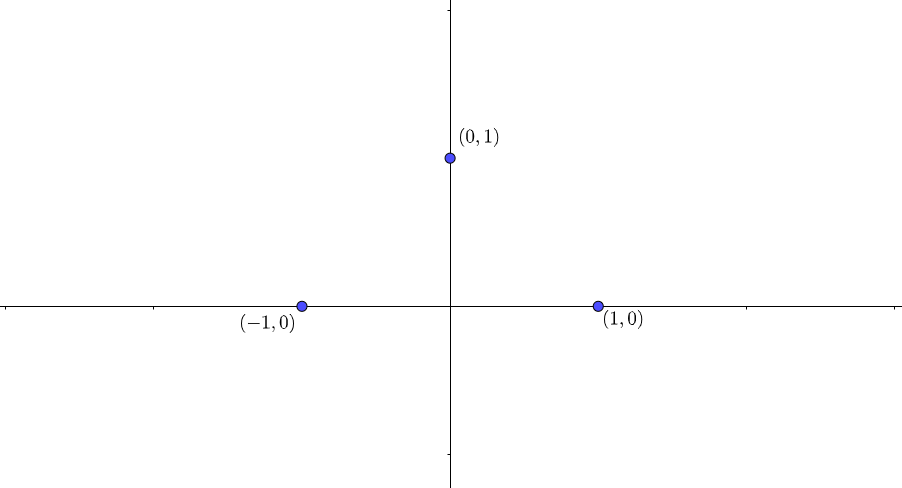
媒介変数表示されたグラフの描き方
さて、あとは曲がり方の問題です。
これは曲がり方についての記事で紹介した通り、1階微分\(\frac{dy}{dx}\)の極限を調べることでわかります。


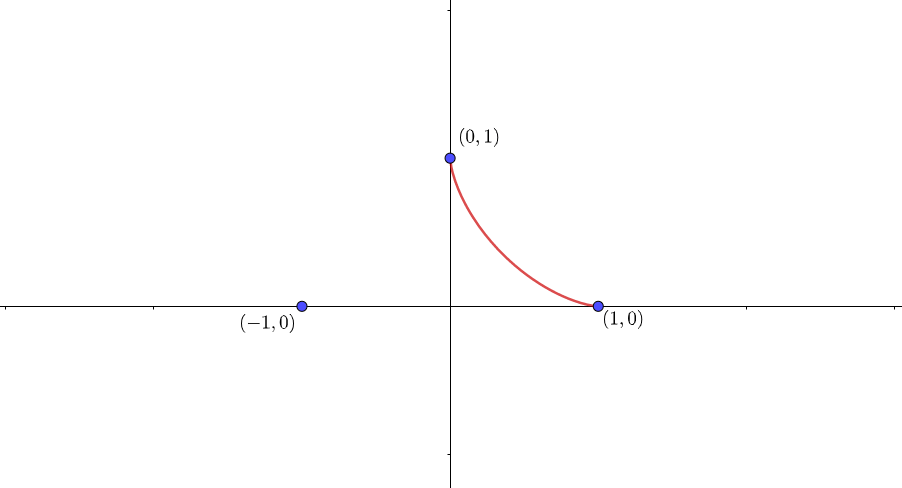
$$\lim_{t\to \pi -0} \frac{dy}{dx} = 0$$

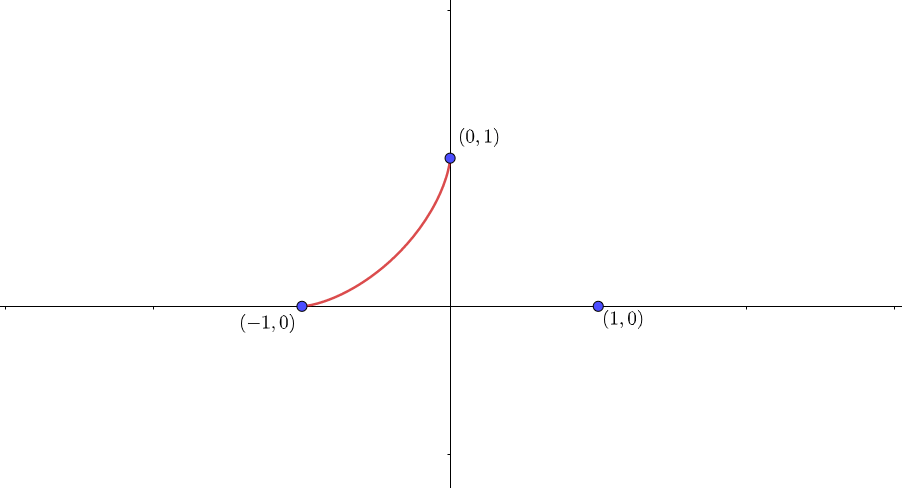
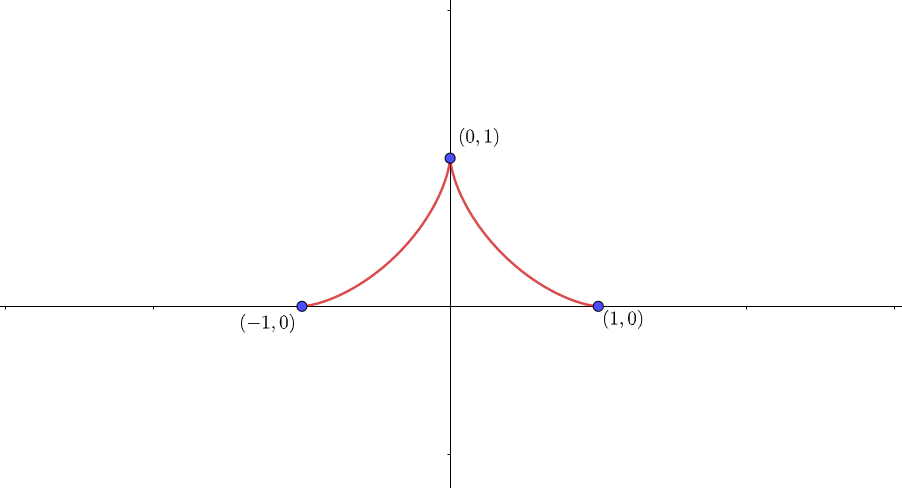
よって、グラフは下図となります。


まとめ

まとめ
媒介変数表示されたグラフを描くためには、
- \(\frac{dx}{dt},\frac{dy}{dt},\frac{dy}{dx}\)を求め、
- \(\frac{dx}{dt}=0,\frac{dy}{dt}=0\)となる\(t\)の値を求め、
- それを元に増減表を描き、グラフで大まかな点を打つ。
- 最後にその2点間のカーブの仕方を極限で調べればOK!
正直な話、2階微分を強引にやってしまえばいらないテクニックかもしれません。
ですが、『ラクして効率的に解く』、それが数学です。
計算ミス・時間ロスをしないように効率的に解く努力をしていきましょう!
以上、「媒介変数表示のグラフの描き方」についてでした。
チェック問題
例題
次のような媒介変数表示で定義される点\((x,y)\)はどのような図形を描くか。
$$\left\{ \begin{array}{l} x=(1+\cos\theta)\cos\theta \\ y=(1+\cos\theta)\sin\theta \end{array} \right. \ (0≦\theta≦\pi)$$
\(x,y\)ともに\(\theta\)について微分すると、
\(\frac{dx}{d\theta}=0\)のとき、\(\theta =0, \frac{2}{3}\pi, \pi\)
\(\frac{dy}{d\theta}=0\)のとき、\(\theta = \frac{\pi}{3},\pi\)
よって増減表は次のようになる。
| \(\theta\) | \(0\) | \(\cdots\) | \(\frac{\pi}{3}\) | \(\cdots\) | \(\frac{2}{3}\pi\) | \(\cdots\) | \(\pi\) |
| \(\frac{dx}{d\theta}\) | \(-\) | \(-\) | \(-\) | \(0\) | \(-\) | \(-\) | |
| \(x\) | \(2\) | \(\searrow\) | \(\frac{3}{4}\) | \(\searrow\) | \(-\frac{1}{4}\) | \(\searrow\) | \(0\) |
| \(\frac{dy}{d\theta}\) | \(+\) | \(0\) | \(-\) | \(-\) | \(-\) | \(0\) | |
| \(y\) | \(0\) | \(\nearrow\) | \(\frac{3}{4}\sqrt{3}\) | \(\searrow\) | \(\frac{\sqrt{3}}{4}\) | \(\searrow\) | \(0\) |
| \((x,y)\) | \((2,0)\) | \(\left(\frac{3}{4},\frac{3}{4}\sqrt{3}\right)\) | \(\left(-\frac{1}{4},\frac{\sqrt{3}}{4}\right)\) | \((0,0)\) |
媒介変数の微分法より、
$$\lim_{\theta\to \frac{\pi}{3}+0}=0$$
$$\lim_{\theta\to \frac{2}{3}\pi-0}=\infty$$
$$\lim_{\theta\to \frac{2}{3}\pi+0}=-\infty$$
$$\lim_{\theta\to \pi -0}=0$$
より、増減表は次のようになる。
| \(\theta\) | \(0\) | \(\cdots\) | \(\frac{\pi}{3}\) | \(\cdots\) | \(\frac{2}{3}\pi\) | \(\cdots\) | \(\pi\) |
| \(\frac{dx}{d\theta}\) | \(-\) | \(-\) | \(-\) | \(0\) | \(-\) | \(-\) | |
| \(x\) | \(2\) | \(\searrow\) | \(\frac{3}{4}\) | \(\searrow\) | \(-\frac{1}{4}\) | \(\searrow\) | \(0\) |
| \(\frac{dy}{d\theta}\) | \(+\) | \(0\) | \(-\) | \(-\) | \(-\) | \(0\) | |
| \(y\) | \(0\) | \(\nearrow\) | \(\frac{3}{4}\sqrt{3}\) | \(\searrow\) | \(\frac{\sqrt{3}}{4}\) | \(\searrow\) | \(0\) |
| \((x,y)\) | \((2,0)\) |
|
\(\left(\frac{3}{4},\frac{3}{4}\sqrt{3}\right)\) |
|
\(\left(-\frac{1}{4},\frac{\sqrt{3}}{4}\right)\) |
|
\((0,0)\) |


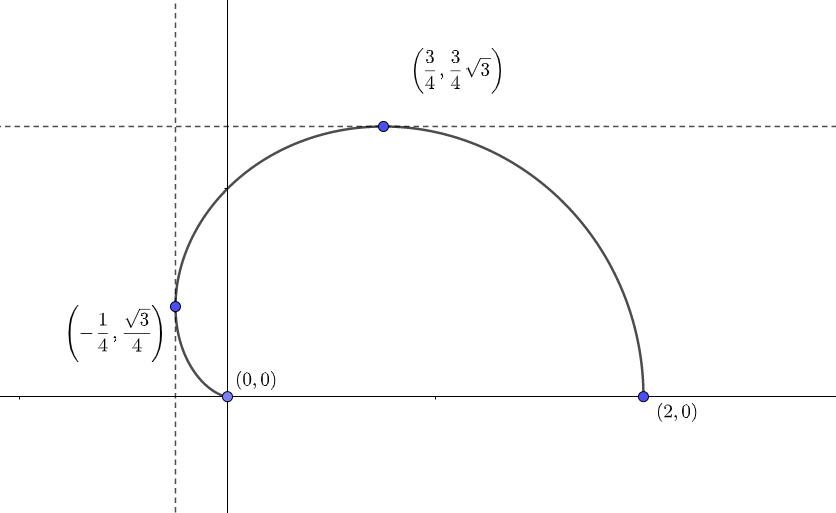
以上から、求めるグラフは次のようになる。