Today's Topic
感覚的なリミットの使い方、意味




この記事を読むと、この意味がわかる!
- 極限で考えたいことと、メリット
- 数列の極限と関数の極限の大まかな違い
Contents
極限基本講座|極限とは?数列から考える数学的な『近づける』

極限というのは、簡単に説明すると2つの点を、一方の点を動かすことで近づけるということをイメージしています。
 一方の点を他方に近づけるというイメージ
一方の点を他方に近づけるというイメージ数学ではこれを
と書きます。
ただしこの近づける、というのはかなり微妙なニュアンスを含んでいます。
例えば点Bを点Aに近づける場合、点Bは点Aと完全に重なることはありません。

また近づけ方も重要です。
数直線上において、『点Bを点Aに近づける』という考え方でも、右から近づくのか、左から近づくのか、が考えられます。
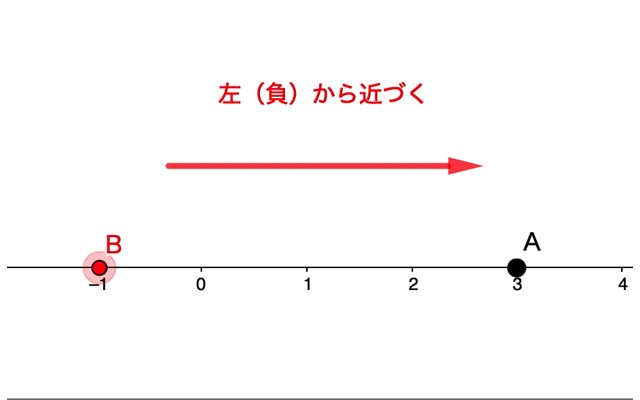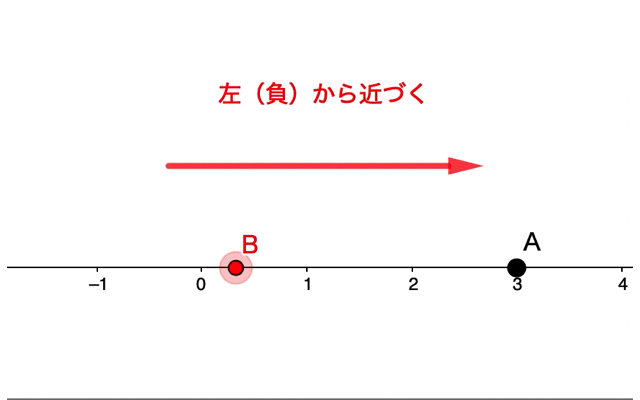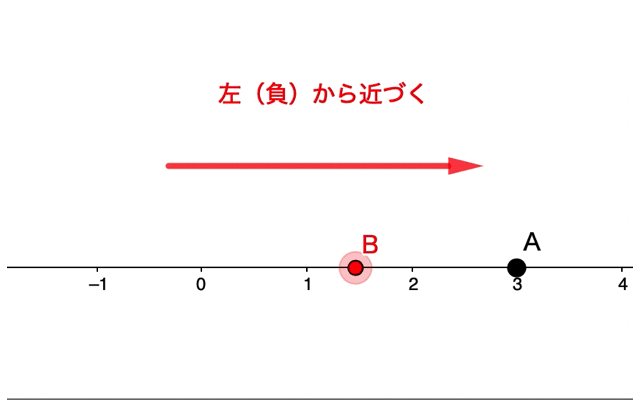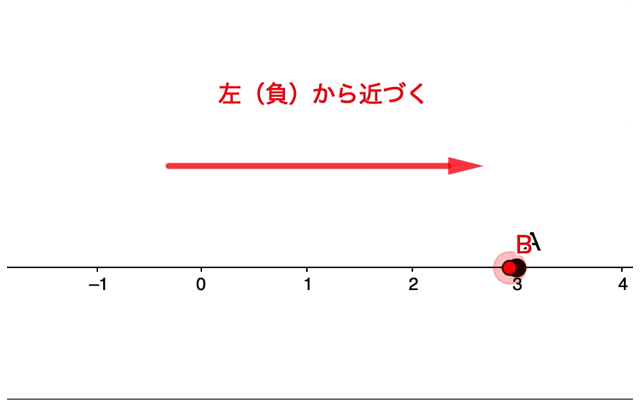
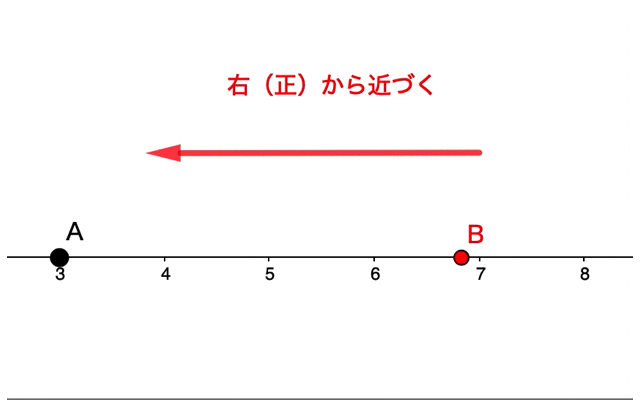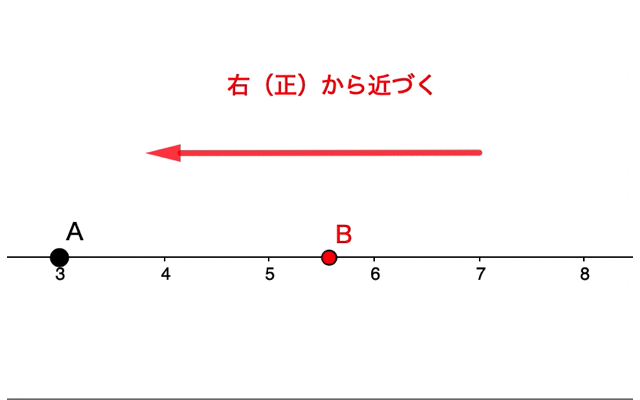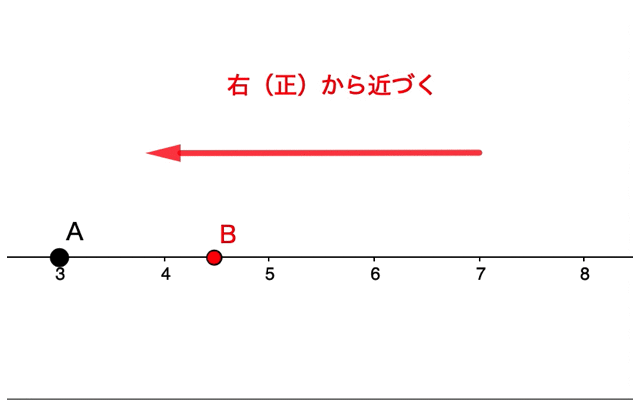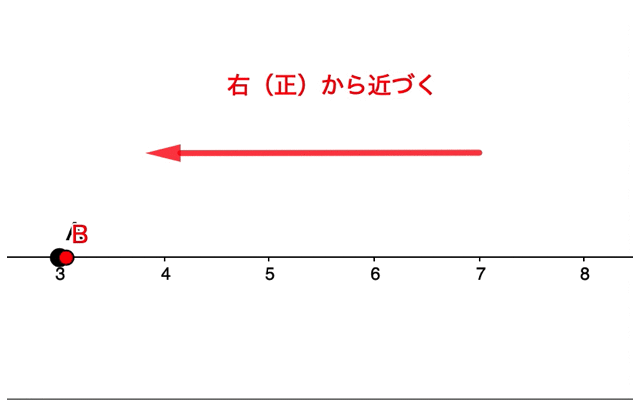

このような極限の考え方に何の意味があるのでしょうか。
実は数学の計算には「\(x=1\)だと困るけど、\(x=0.999\cdots\)だと嬉しい」ことがたくさんあります。
これについては、後述する『極限を考えるメリット』でご紹介します。
まずは数列の極限と、関数の極限の違いについてお話しします。
極限基本講座|数列の極限
数列の極限は、基本的に番目がどんどん大きくなっていったとき、数列が全体的にどんな値に近づくかを考えます。
このとき、数列を関数のグラフだと思って考えるとイメージしやすくなります。
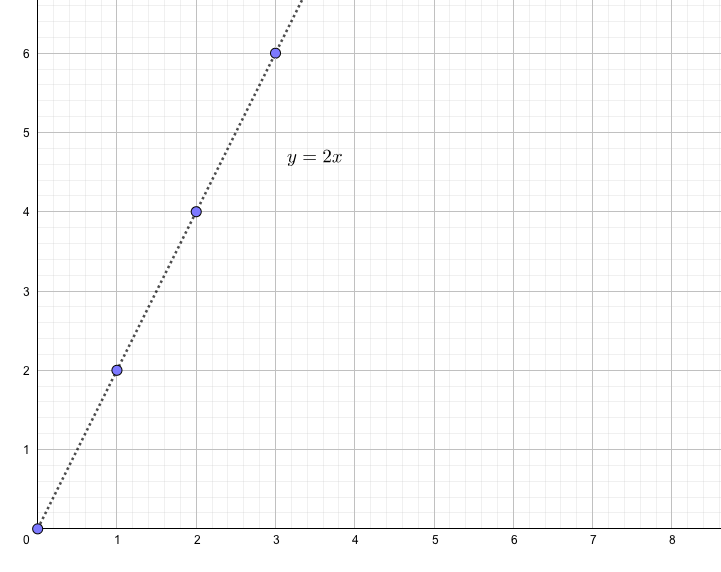
例えば数列\(a_n=2n\)において、番目\(n\)をどんどん大きくしていった場合、
と各項の値は無限大に大きくなっていきます。これを発散といい、
$$a_n \underset{n\to \infty}{\longrightarrow} \infty$$
のように表します。

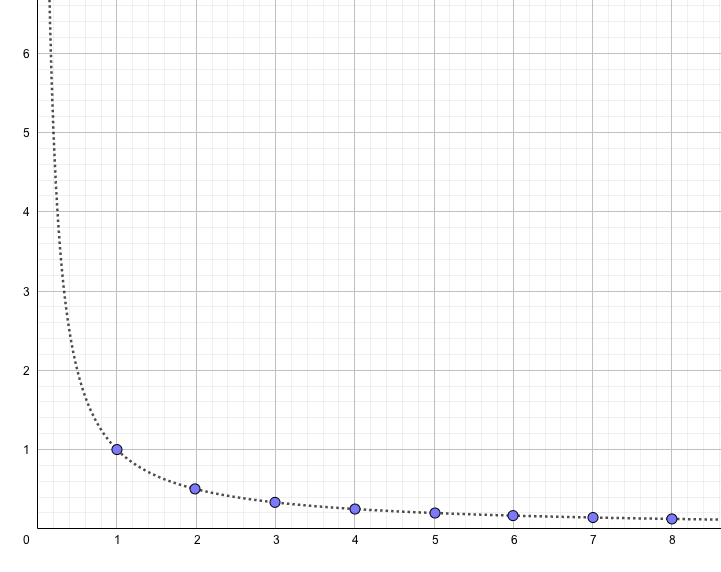
一方で、数列\(b_n=\frac{1}{n}\)において、番目\(n\)をどんどん大きくしていった場合、
と各項の値はどんどん小さく、最終的に0に超近くなっていきます。これを0に収束といい、
$$b_n \underset{n\to \infty}{\longrightarrow} 0$$
のように表します。



数列の極限について、詳しくは別記事で取り扱います。より網羅的に、得点源につなげたい人はご覧ください。
参考【収束・発散の速さ】絶対に覚えておきたい極限の裏公式|見た瞬間に極限がヒラメク!
極限基本講座|関数の極限
関数の極限は、数列の極限と基本的には同じですがより広い意味で扱います。
例えば数列では\(n\rightarrow \infty\)しか扱いませんでしたが、関数では\(x\rightarrow 0\)や\(x\rightarrow \frac{\pi}{2}\)といった特定の値に近づけることも考えます。
ちょっと厄介なのが、近づけ方を考える点です。
冒頭でも書いた通り、関数の極限では『右から近づけるのか』、『左から近づけるのか』まで考慮します。
例えば、次のグラフの\(x=3\)付近の値について考えてみましょう。
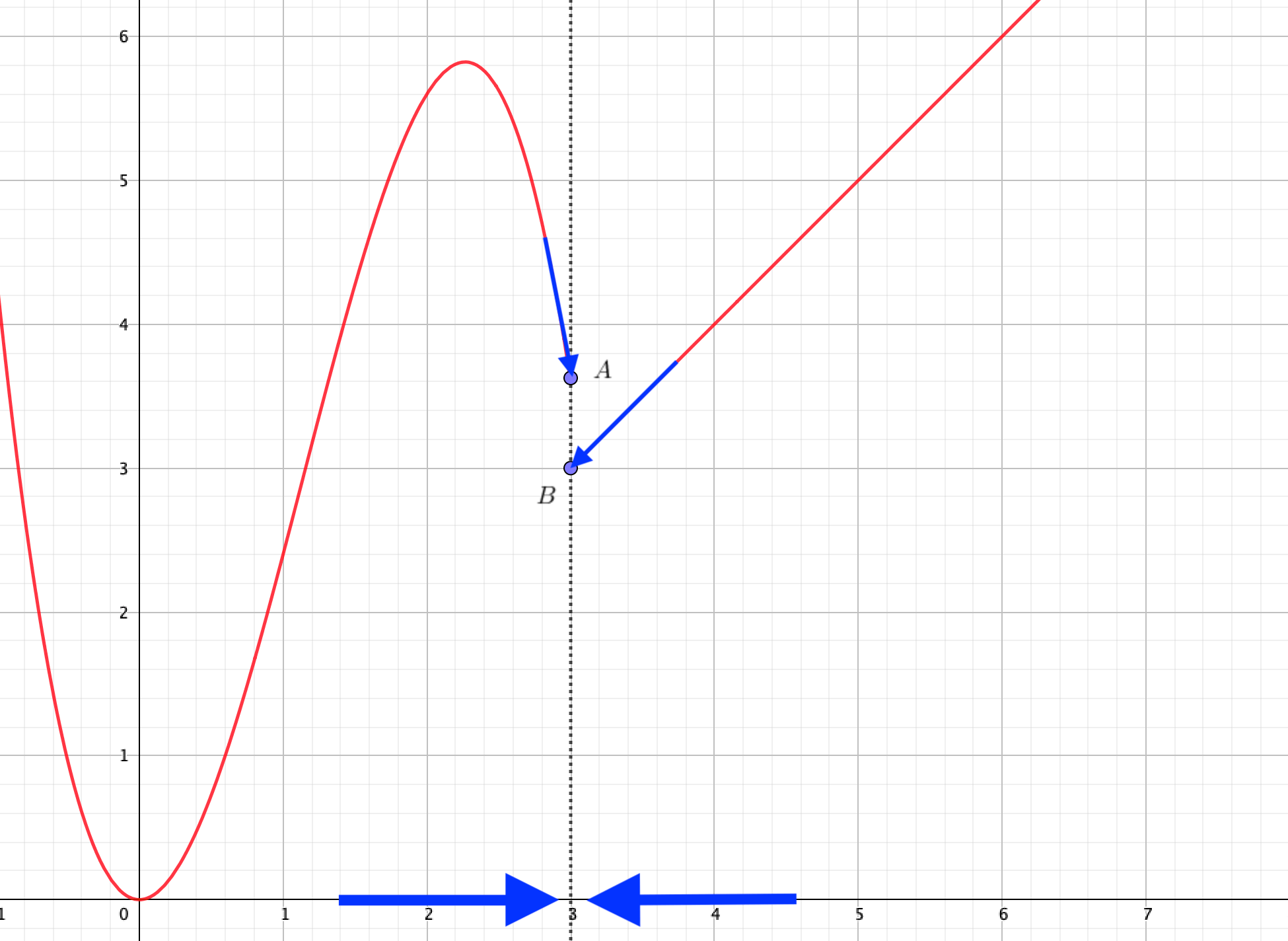
\(x\rightarrow3\)を考えたとき、
- 左から近づける→点Aに収束
- 右から近づける→点Bに収束
と、極限値が異なることがわかります。
このように近づけ方によって極限値が変わる場合、関数の極限では極限がないものとして定義します。
そのため、グラフをイメージできる人がこの単元は強くなります。
ちなみに数列の極限は\(n\rightarrow\infty\)のみを考え、\(n\)が自然数しかとらないことから、この極限が一致しない問題は起きません。
関数の極限について、詳しくは別記事で取り扱います。数Ⅲをする人は是非ご覧ください。
参考【関数の極限】見落としがちな解法の重要ポイントを徹底解説!迷わずに解けるようになろう!
極限基本講座|極限を考えるメリット

数学では極限という考えが出現してから、『等しくなる』と『近くなる』は明確に区別されました。
『近くなる』ということが数学的に定義できたことで、数学の世界で「〜とみなすことができる」という妥協がOKになりました。
1つ簡単な例を見てみましょう。
数学では\(\frac{1}{0}\)という数は存在しません。
証明
\(\frac{1}{0}\)という数が存在すると仮定する。
\(\frac{1}{0}=a\)と表すと、両辺に0をかけることで\(1=a\times 0\)となる。
だが、0をかけて0以外の数になるような\(a\)は存在しない。よって矛盾。
以上より、\(\frac{1}{0}\)という数は存在しない。
ここで、関数\(f(x)=\frac{1}{x}\)の\(x\)を右から0に近づけてみましょう。
すると、グラフを見てもらうとわかる通り、\(f(x)\)はどんどん大きくなっていきます。
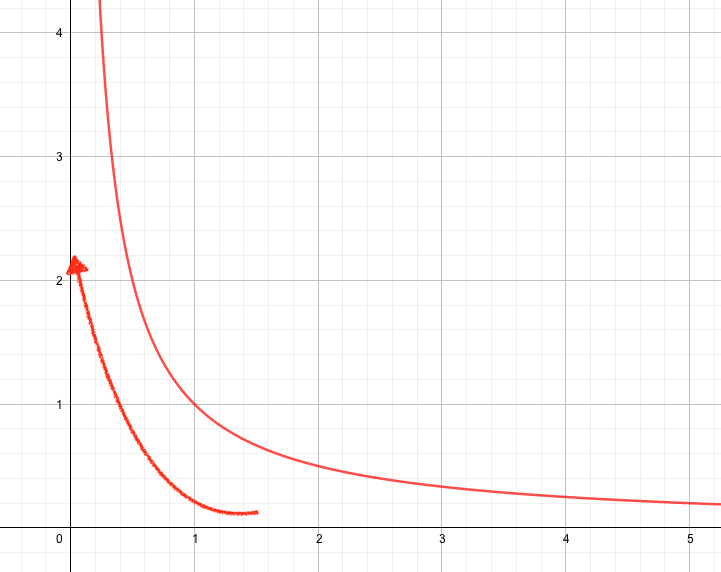
つまり\(x\)を0に近づけると、関数\(f(x)\)は無限大に発散するということが言えます。
なので、
と書き表すことができますね。
このように
(※見切れている場合はスクロール)
というわけで、特別に\(\frac{1}{0}\)を考えられるわけです。
極限基本講座|極限の計算にはウソがある
ここまでみてきた極限ですが、極限の計算方法が結構厄介なので、ここで紹介しておきます。
極限で初めて出てきたリミットには、分配法則のような性質があります。
しかし、その分配法則が成り立つのは、収束する時のみという制限が設けられています。
にもかかわらず、理系脳の方たちは、この条件を無視して解答にたどり着くことができます。
この計算方法が大きな分かれ目なので、こちらの記事でじっくり紹介しますね。
参考【極限の性質】リミットには分配法則が成り立つが、特殊な解釈をしているゾ!
極限基本講座|まとめ:極限は「〜に近づくか」

まとめ
- 数列の極限は\(n\rightarrow\infty\)のみを考える。グラフを意識すると考えやすくなる。
- 関数の極限は\(x\)をいろんな値に近づけることができるが、近づけ方も考える必要がある。
- 極限を考えると数学的に「おおよそどんな値になるか」を考えられる。
極限の理解は、高校数学のうちでは直感的なもので十分です。
数学的に証明しようとすると、大学数学の内容になってしまいます(\(\varepsilon - N\)論法というものを使います)。
それゆえ、数学の中ではイレギュラーな『証明は詳しくわかんないけど、公式だけ覚えて解いてね』というニュアンスが感じられます。
とは言っても、大学で数学を学ぶ上でもこの直感は非常に大事です。
極限が何を意味しているかをぜひ理解してください。
以上、「イメージできる極限」でした。








