Today's Topic
- 指数関数の極限を考えるためには、底の数に着目し、指数が大きくなるほど値が増えるのか、小さくなるのかを考えれば良い。
- 指数関数の極限で不定形になる場合は、積の形に持っていくと楽な場合が多い。



この記事を読むと、この意味がわかる!
- $$\lim_{x\to\infty} (2^x-3^x)$$
- $$\lim_{x\to\infty} 2^{\frac{1}{x}}$$

Contents
指数関数の極限
まずここでは、指数関数の極限の特徴をざっとまとめてみます。
簡単に特徴をとらえるために、グラフを考えるといいです。
ポイント
関数\(y=a^x\)について、
\(1 < a\)のとき
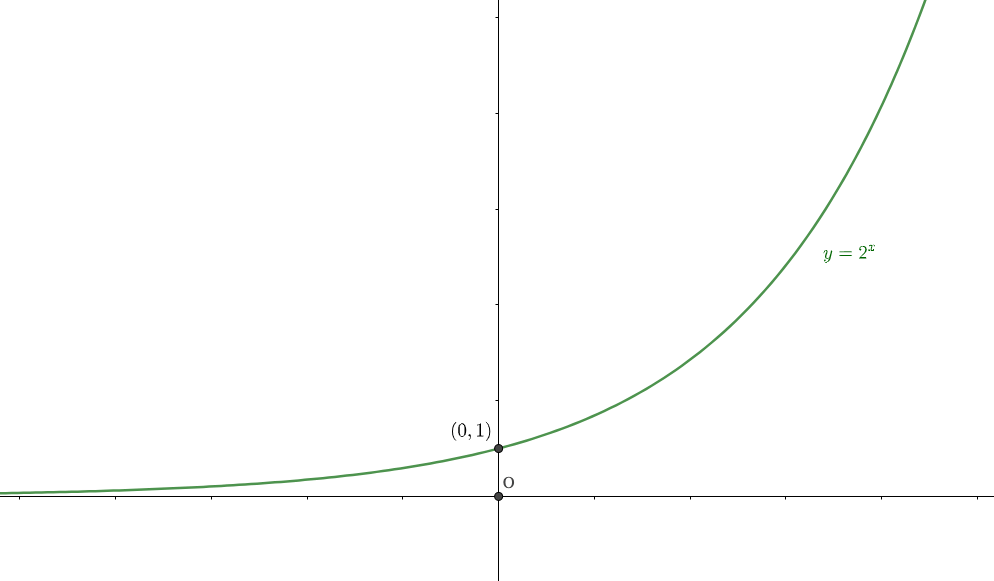
$$①\lim_{x\to \infty} a^x = \infty$$
$$②\lim_{x\to -\infty} a^x = 0$$
\(0< a < 1\)のとき
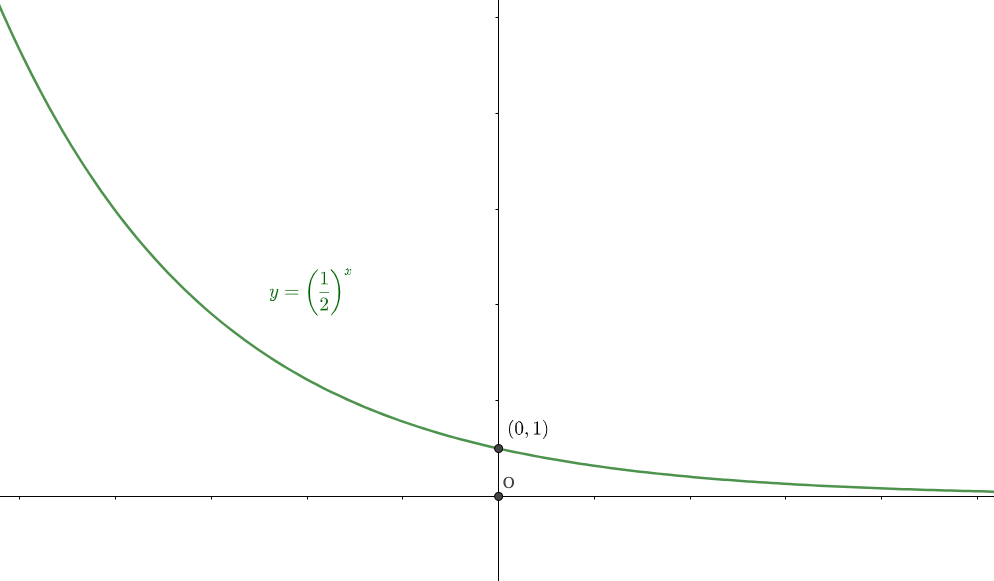
$$①\lim_{x\to \infty} a^x = 0$$
$$②\lim_{x\to -\infty} a^x = \infty$$


【実は覚えること0】指数関数の極限の特徴
ざっと特徴を網羅しただけだと、暗記項目のようにも見えますね。
しかし、実はグラフさえ考えなくても指数関数の本質を理解しておけば、これらの性質はその場で瞬時にひらめくものです。

①\(x\to \infty\)の場合について
具体的に\(y=2^x\)について考えてみましょう。
これは日本語訳してみると「2を\(x\)回掛けたものが\(y\)」となりますね。
そのため、\(x\)の値が次第に増えていくと、2をかける回数が増えていくということなので、値はどんどん大きくなっていくことは容易に想像できるでしょう。
つまり
であることは、簡単にわかるということです。
では\(y=\left(\frac{1}{2}\right)^x\)ではどうでしょうか。
1より小さく0より大きい数、すなわち1より小さい分数は掛けるほど値が小さくなっていきますね。
そのため、\(x\)の値が次第に増えていくと、分数をかける回数が増えていくということなので、値はどんどん小さくなりますね。

つまり
であることも、簡単にわかりましたね。
メモ
ちなみにここでは、日本語訳として「2を\(x\)回掛けたものが\(y\)」としましたが、これは\(x\)が自然数の範囲でしか通用しません。
本来、グラフを考えている以上\(x\)は連続、すなわち実数全体であるべきです。
そのため正しくは、指数法則によって考える必要がありますが、結局「2を\(x\)回掛けたものが\(y\)」と考えたときと結果は変わりません。
が、できれば指数法則をしっかり理解した上で考えられるようになっておくといいでしょう。
②\(x\to -\infty\)の場合について
こちらもまず、\(y=2^x\)について考えてみましょう。
\(x\to -\infty\)とは負の無限大、すなわちマイナス方向に値をどんどん大きくしていくという意味です。
指数法則を思い出してみましょう。
指数が負の場合、
のように、底\(a\)が逆数\(\left(\frac{1}{a}\right)\)となるのでしたね。
負の無限大を考えている場合、指数はマイナスとみなしてよく、\(x = -x' \ (x' > 0)\)と考えると
と表現できるわけです。
これは\(x\)の値がマイナス方向に大きくなるほど、分数をかける回数が増すということを表していますね。
つまり負の無限大を考えると、次第に値が小さくなっていきますが負にはならないので
と分かります。
では\(y=\left(\frac{1}{2}\right)^x\)ではどうでしょうか。
先ほどと同じく\(x = -x' \ (x' > 0)\)と考えると、
となるわけです。
これは\(x\)の値がマイナス方向に大きくなるほど、2をかける回数が増すということを表していますね。
つまり負の無限大を考えると、次第に値が大きくなっていきますので
と分かります。
②の場合の特徴は、指数が負になると底が逆数になるという性質のせいで、①の性質が入れ替わったような感じになります。
問題への応用
指数関数は①、②でみたように
のように、途中の過程で極限が変化しない、単調変化が特徴です。
よって指数関数の極限であることを見抜けば、あとは値が無限に大きくなるか、0に近づくかを判断するだけでOKです。
例題
$$\lim_{x\to\infty} (2^x-3^x)$$

この状態のままでは、関数が無限になるのか、小さくなっていくのか判断できません。
そこで全体を\(3^x\)でくくってみます。
すると、
$$\left(\frac{2}{3}\right)^x \underset{x\to \infty}{\longrightarrow} 0$$
とわかるので、
と表現することができました。
指数関数の極限で不定形になる場合、くくるなどして「指数関数\(\times\)なんとか」のような形に持っていくと良い。
まとめ

まとめ
- 指数関数の極限を考えるためには、底の数に着目し、指数が大きくなるほど値が増えるのか、小さくなるのかを考えれば良い。
- 指数関数の極限で不定形になる場合は、積の形に持っていくと楽な場合が多い。
今回の内容は正直言って、あまり難しくはありません。
なぜなら底の数をみて、どんどん大きくなるか小さくなるかを考えれば良いだけですから。
ただこの考え方自体は、対数関数の極限の暗記もなくしてくれるので、ぜひ習得していってください。
以上、「指数関数の極限について」でした。
チェック問題
例題
$$\lim_{x\to\infty} 2^{\frac{1}{x}}$$
底の数を見ると2、つまり1より大きい数なのでかけるほど大きくなっていきます。
指数\(\frac{1}{x}\)は\(x\to \infty\)の場合、\(\frac{1}{x}\to 0\)となっています。
つまり、0乗に近づいていくということを表しているので、
となります。








