Today's Topic
- 対数関数の極限を理解するためには、グラフを考えれば良い。
- リミットとログは入れ替えることができる!




この記事を読むと、この意味がわかる!
- 対数関数の極限の捉え方
- 対数関数の極限で頻出の『入れ替え法則』

対数関数の性質

対数関数は指数関数の極限とは違い、グラフを考えた方が極限を捉えやすいです。

底が1より大きいとき
対数関数\(y=\log_a x\)に対して、底数\(a\)が\(1<a\)を満たすとき、グラフは次のようになります。

グラフを見てわかる通り、
$$\lim_{x\to +0} \log_a x = -\infty$$
の2つの性質が成り立ちます。

底が1より小さい分数のとき
対数関数\(y=\log_a x\)に対して、底数\(a\)が\(0<a<1\)を満たすとき、グラフは次のようになります。
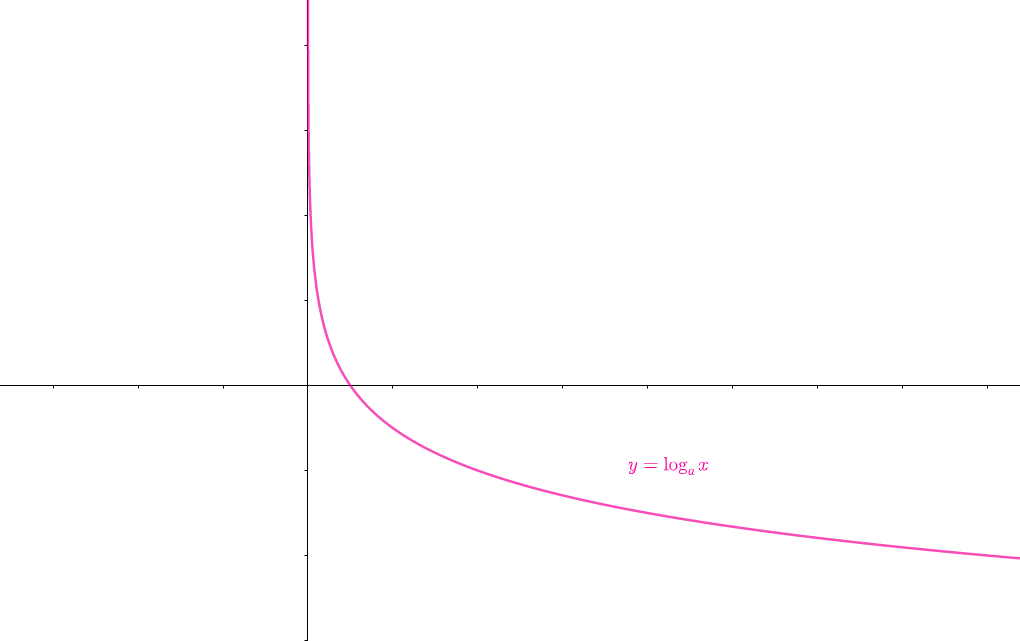
グラフを見てわかる通り、
$$\lim_{x\to +0} \log_a x = \infty$$
の2つの性質が成り立ちます。
重要性質『入れ替え法則』
さて、上記でご説明した性質は至ってシンプルかつ直感的でした。
しかし対数関数で最も重要な性質は、次の入れ替え法則が成り立つことです。
入れ替え法則
$$ \log \left(\lim_{x\to\infty} y\right) = \lim_{x\to\infty} \log y$$

例
次の公式を示せ。
$$\lim_{h\to 0}\frac{\log(1+h)}{h} = 1$$
ネイピア数の定義を考える。
$$\lim_{h\to 0}\left(1+h\right)^{\frac{1}{h}}=e$$
両辺に自然対数をとると、
$$\log \left(\lim_{h\to 0}\left(1+h\right)^{\frac{1}{h}}\right)=\log e = 1$$
入れ替え法則を使うと、
\begin{align} 左辺 &= \log \left(\lim_{h\to 0}\left(1+h\right)^{\frac{1}{h}}\right) \\\ &= \lim_{h\to 0} \log\left(1+h\right)^{\frac{1}{h}}\\\ &= \lim_{h\to 0} \frac{1}{h} \log\left(1+h\right)\\\ \end{align}
よって、
$$\lim_{h\to 0}\frac{\log(1+h)}{h} = 1$$
という公式が得られる。

『入れ替え法則』の証明

対数関数\(y=f(x)=\log_a x\)は\(0<x\)において、底数\(a\)によらず連続な関数になっていることはグラフを見てわかると思います。
さて、連続と言いましたが、そもそも数学における連続とは次のような定義を満たしています。
定義
関数\(f(x)\)が\(x=a\)で連続であるとは、
(※見切れている場合はスクロール)
を満たしていることを言う。
参考【連続である】って結局ナニ?定義の意味がイメージで簡単に理解できる!
当然対数関数\(f(x)=\log_a x\)は\(0<x\)において任意の点で連続なので、
を満たすので、
が成り立ちます。

でもこの変形って、結局
と考えても同じなので、ログとリミットの順番は入れ替えてもOKということになります。
メモ
今回はグラフから対数関数が連続だと言いましたが、実際は対数関数が連続であることを最初に証明しなければなりません。
あくまで簡単に理解できればいいなと思い端折りました。
興味がある人は大学数学でお勉強してみてください。
まとめ

まとめ
- 対数関数の極限を理解するためには、グラフを考えれば良い。
- リミットとログは入れ替えることができる!
今回扱った性質はとても重要なもので、今後も当たり前のように出てきます。
その中で「無意識」で解くのではなく、しっかり連続が意識されていることを念頭において解けるといいですね。
以上、「対数関数の極限(基礎)」でした。








