Today's Topic
関数\(f(x)\)が\(x=a\)で連続であるとは、
(※見切れている場合はスクロール)
を満たしていることを言う。




この記事を読むと、この問題が解ける!
- 関数\(y=x^3+2x\)は\(x=2\)で連続か。
- 関数$$y=\left\{ \begin{array}{l} x^2\ (x≦2) \\ x+3\ (2<x) \end{array} \right. $$は\(x=2\)で連続か。

グラフが連続であることの定義
まず『関数のグラフが、ずっと繋がっている』ということは、数学的に以下のように定義されています。
定義
関数\(f(x)\)が\(x=a\)で連続であるとは、
(※見切れている場合はスクロール)
を満たしていることを言う。

まずは、見知らぬ数式
について解説していきます。
右極限、左極限について
グラフ上の点A(\(x=a\))と、点Aよりも右側にある適当な点Bに注目してください。
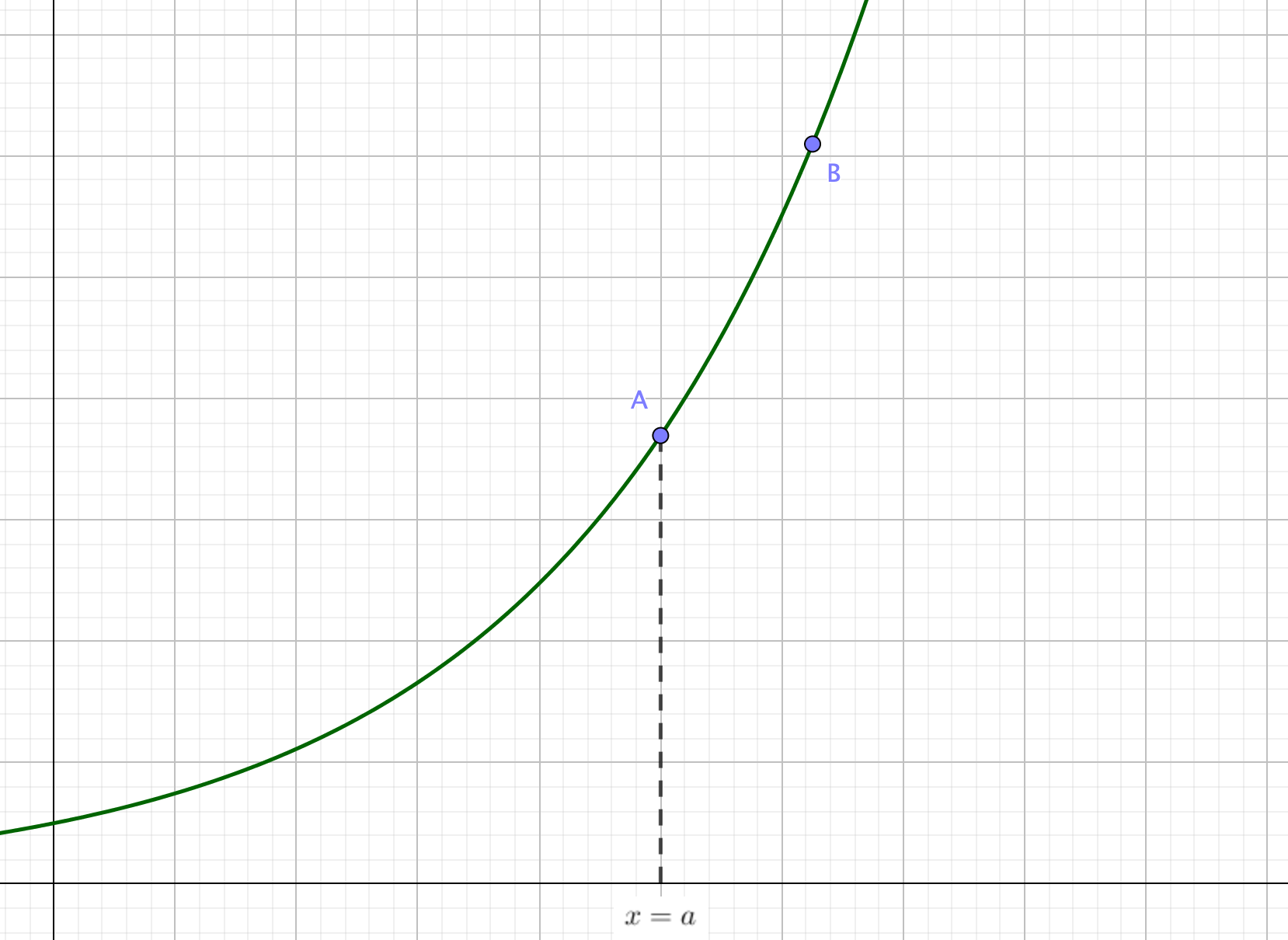
この点Bを点Aに近づけます。
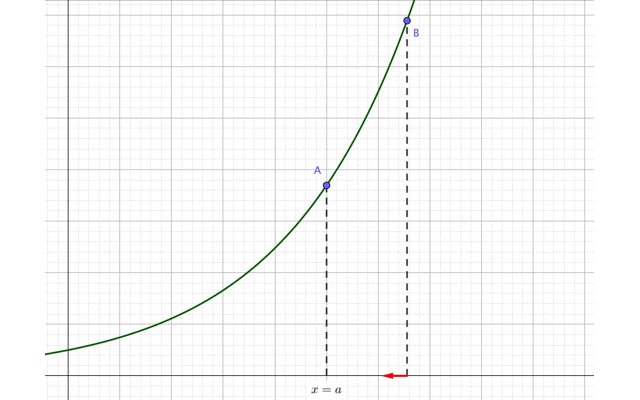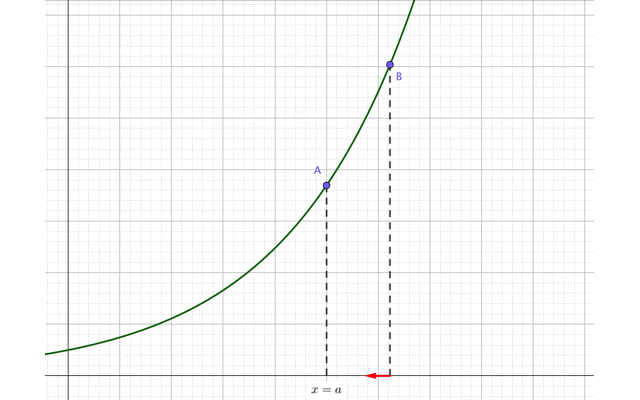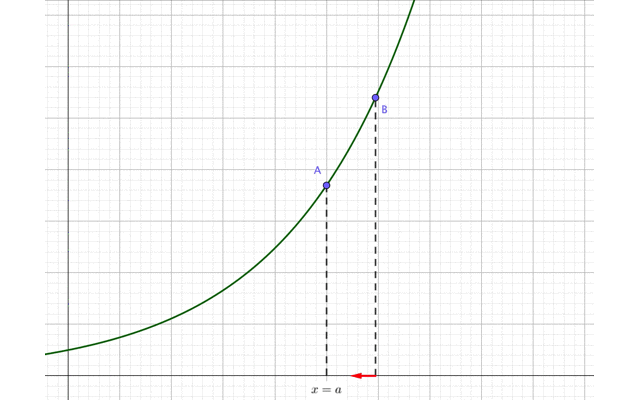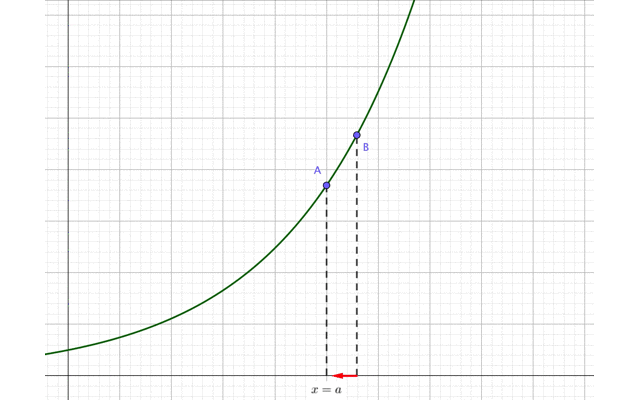
すると、点Bの\(x\)座標は次第に\(x=a\)に近づいていますね。
このように\(x\)が、\(x=a\)に右から近づくことを、
と書きます。
すなわち関数\(f(x)\)上の点A、点B(点Bは点Aよりも右側)を考えて、点Bを点Aに右から近づけていると表したものが
となります。
数学では、これを右極限といいます。
今度は、点Aよりも左側にある点Cを考えてください。
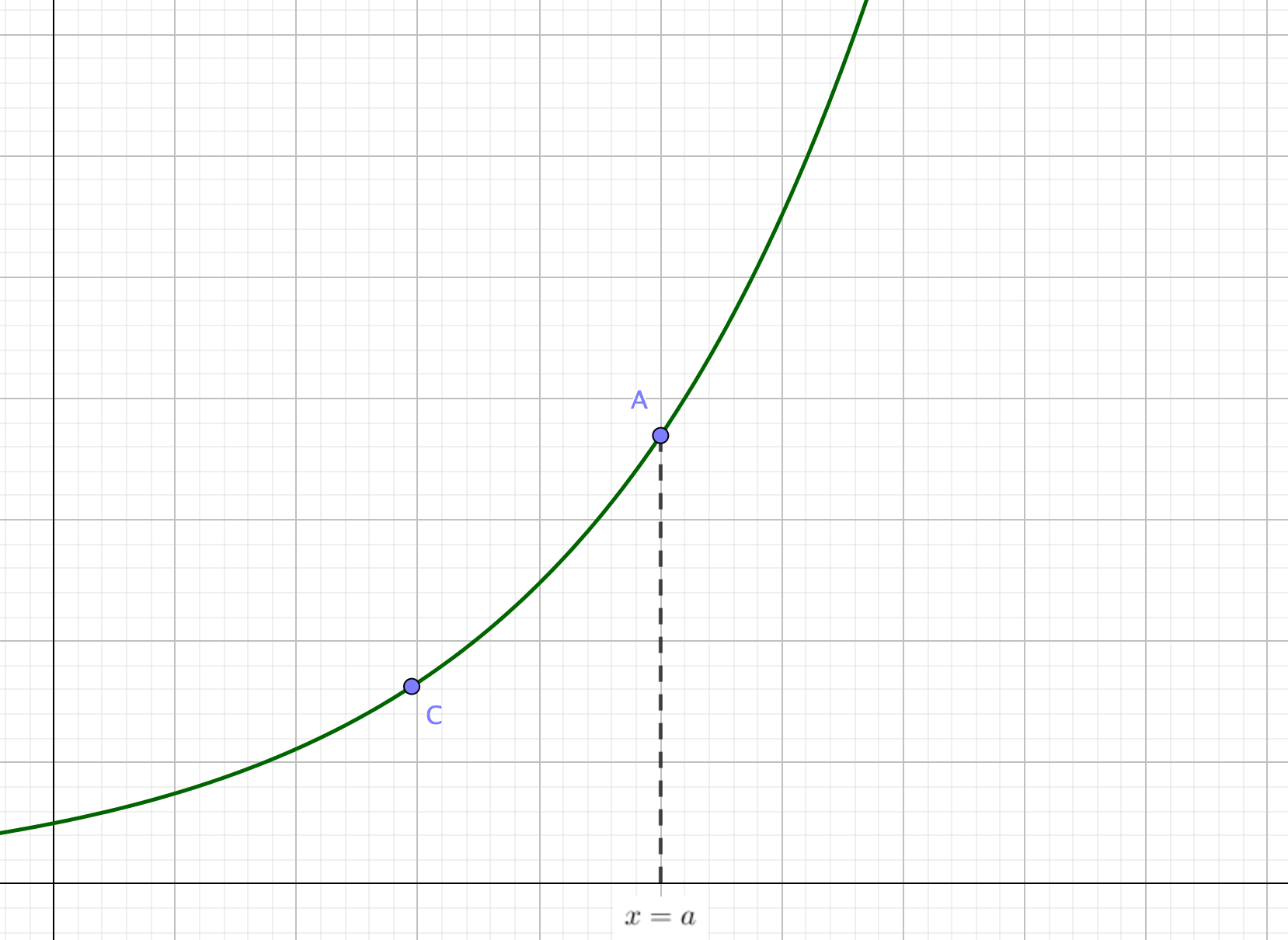
この点Cを点Aに近づけます。
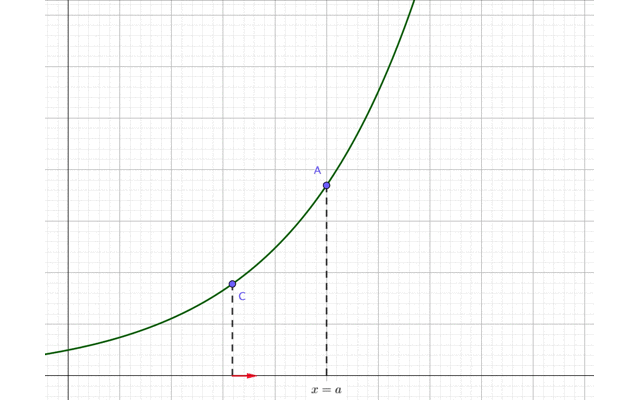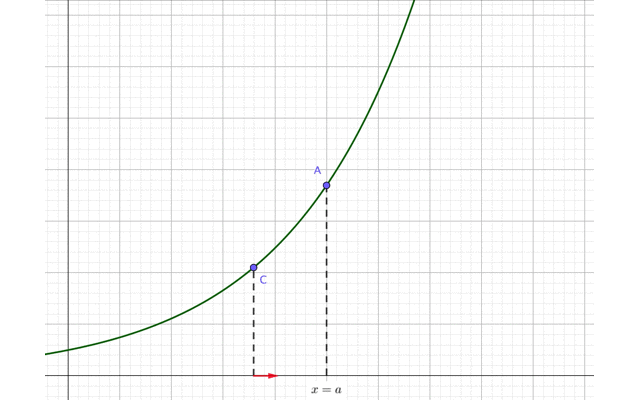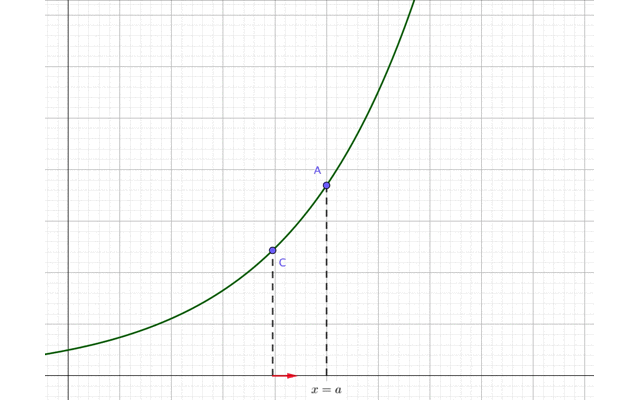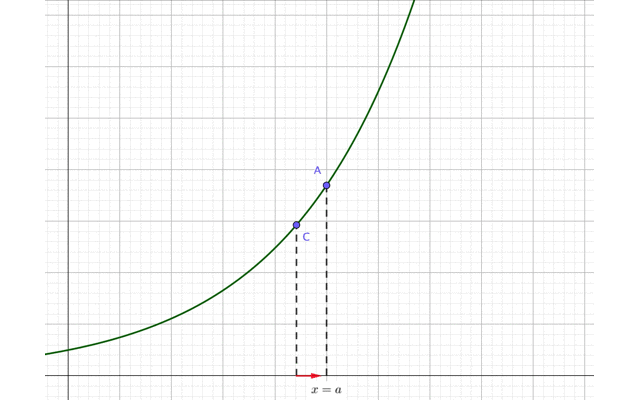
すると、点Cの\(x\)座標も次第に\(x=a\)に近づいていますね。
このように\(x\)が、\(x=a\)に左から近づくことを、
と書きます。
すなわち関数\(f(x)\)上の点A、点C(点Cは点Aよりも左側)を考えて、点Cを点Aに左から近づけていると表したものが
となります。
数学では、これを左極限といいます。
連続のイメージ的な理解
それでは本題の「連続」について解説します。
先ほどの図の点Bと点Cを、同時に点Aに近づけます。
ただし2つの点は点Aを通り過ぎることはありません。
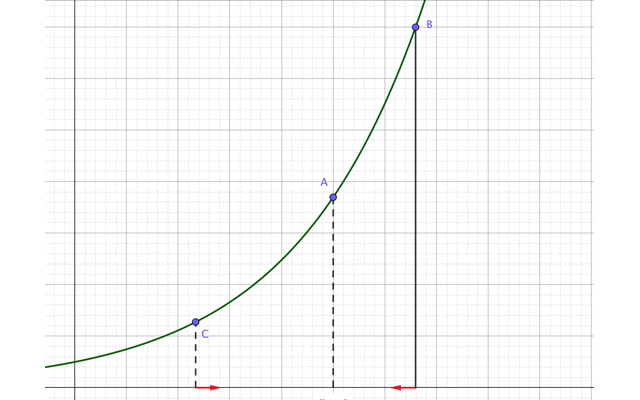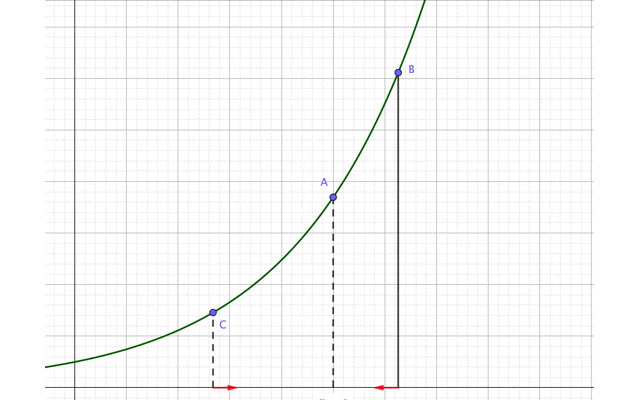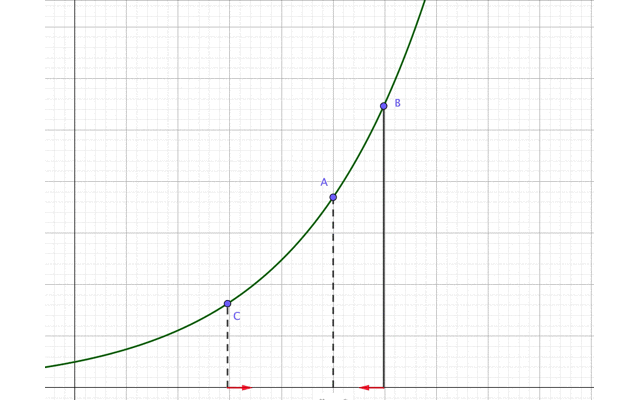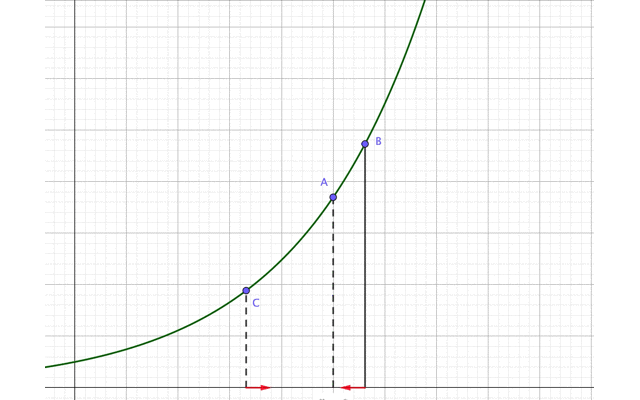
すると点Bと点Cはいつか、点Aでゴッツンコするはずですよね?

実は、これが連続の定義です。
もう一度定義を見てみましょう。
(※見切れている場合はスクロール)
を満たしていることを言う。
を日本語訳すると、
ココがポイント
右と左から同時に2点をある点Aに近づけて、2点が点Aでゴッツンコするとき、その関数は点Aで繋がっている(連続)
と言っているだけなのです。
数学では、
を『\(x=a\)で右連続』、
を『\(x=a\)で左連続』と言います。
すなわち\(x=a\)で連続である、とは\(x=a\)で右連続かつ左連続であるということなんですね。
ちなみに、
かつ
であるとき、
と書きます。
ポイント
すなわち$$\lim_{x \to \color{red}{a}}f(x)$$は右極限と左極限が一致していて初めて書ける式ということになりますね。
連続でない場合
では理解を深めるために、連続していない場合を見てみましょう。
問題
関数\(f(x)=\frac{1}{x}\)は、\(x=0\)で連続か。
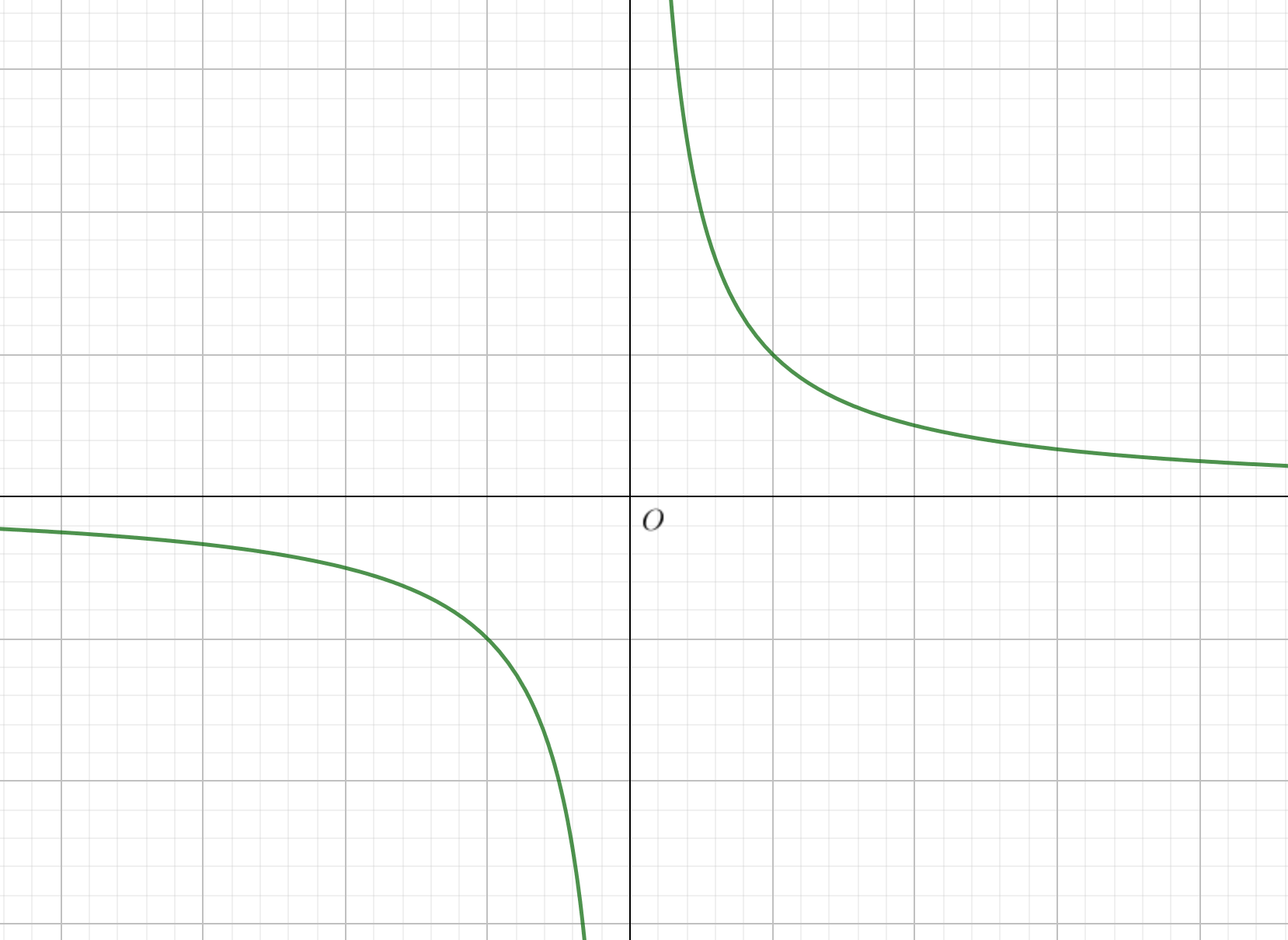
今回は2点A,Bを\(x=0\)に近づけるように動かしましょう。
ただし点Aは原点よりも右側、点Bは原点よりも左側にあるとします。
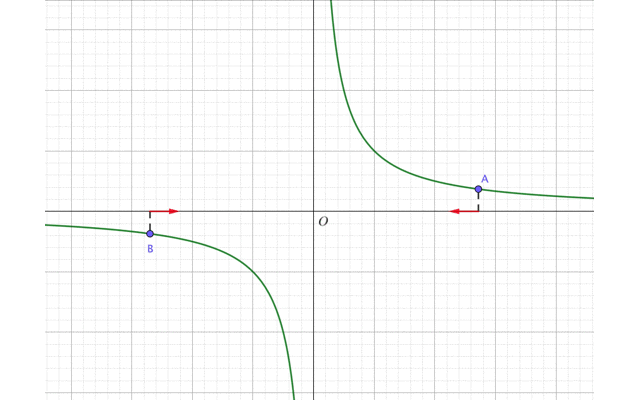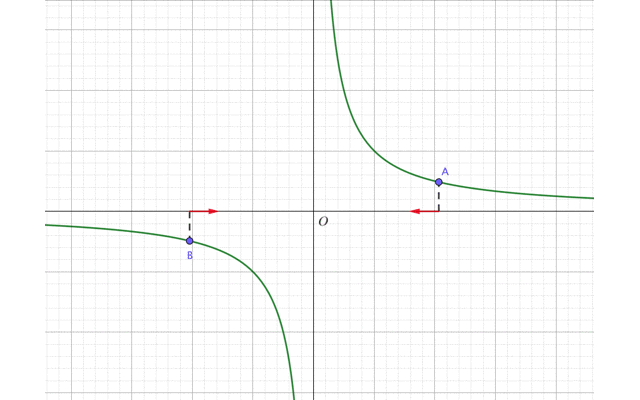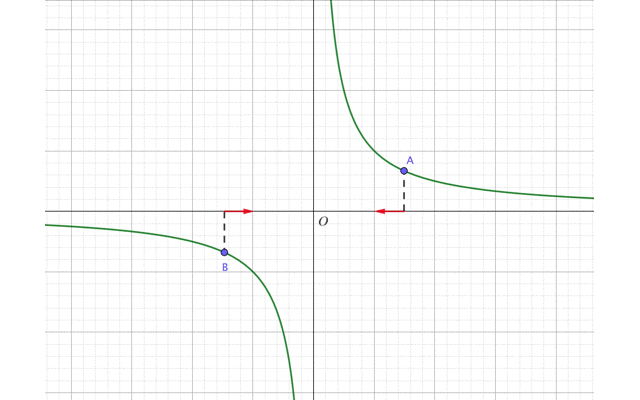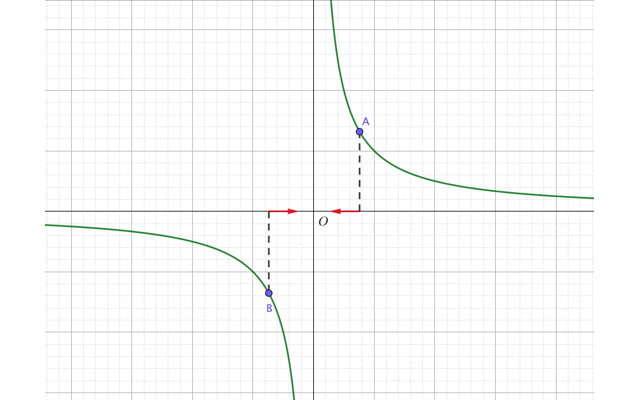
するとグラフは点Aがいるラインだと、\(x\)が0に近づくほど、\(y\)座標は上昇していきます。これを式で表すと、
となります。
ところが点Bのいるラインだと、\(x\)が0に近づくほど\(y\)座標は下降していきますね。これを式で表すと、
となります。
\(+\infty\not= -\infty\)なので、
ですね。
すなわちこの関数は、原点では連続ではないということが(視覚的には当然ですが)数学的にしっかり証明されたことになります。
連続でないことを示すためには、右極限と左極限の値が一致しないことを示せばいい。
部分的な連続
もう一度、先ほどのグラフを考えてみましょう。

このグラフに3点A,B,Cを図のように、とってみます。
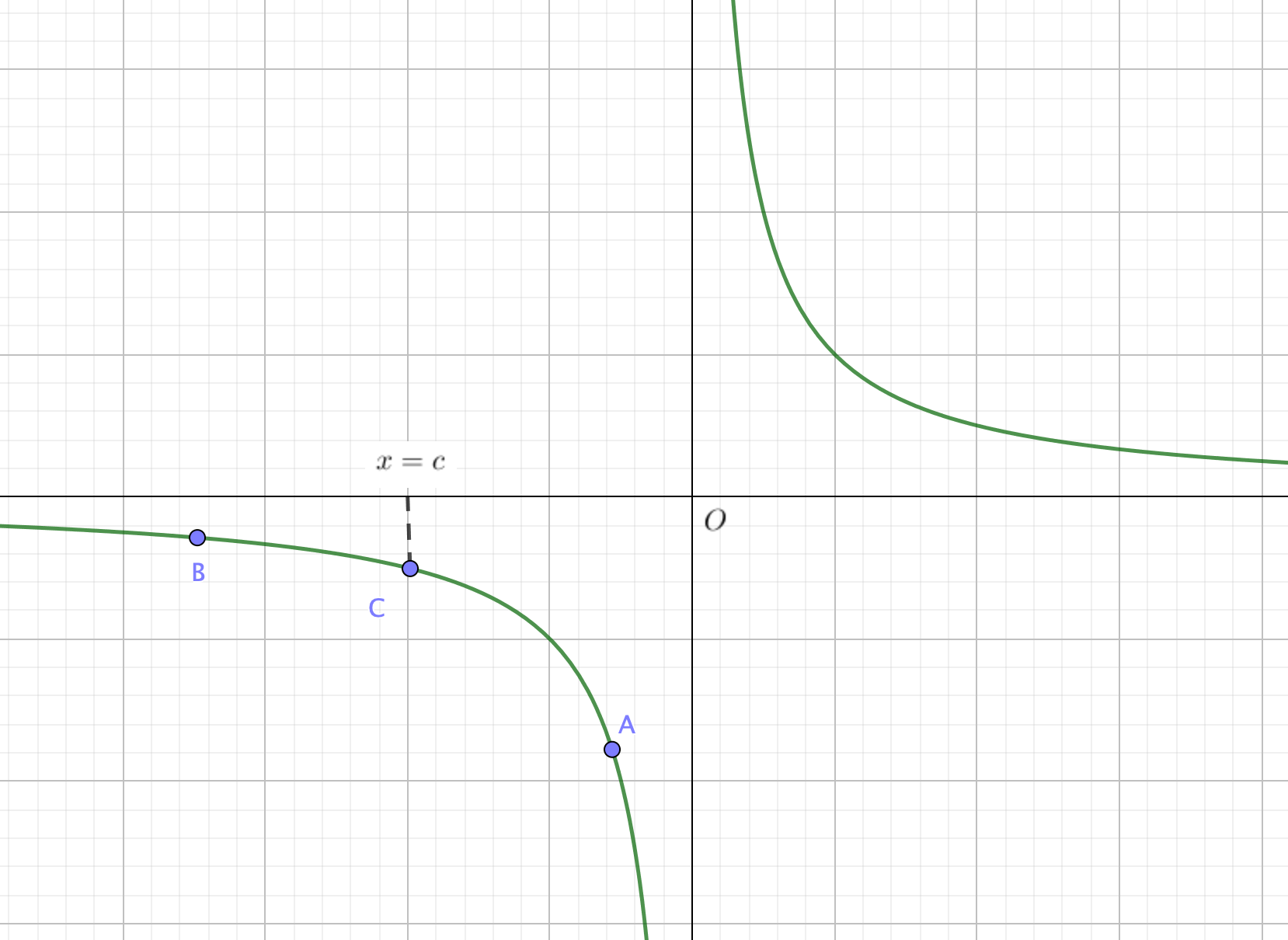
では、2点A,Bを点Cに近づけてみましょう。すると2点は点Cでゴッツンコするように見えますよね?
すなわち、
が成り立ちそうです。
このようにある程度の制限を設けることで、部分的に連続であるということもできます。
数学的にこれをかくと、
\(x<0,c<0\)のとき、\(f(x)=\frac{1}{x}\)は部分的に連続である
となります。
2つの関数の境界が連続か

例題
関数
$$f(x)=\left\{ \begin{array}{l} x^2\ (x≦2) \\ x+3\ (2<x) \end{array} \right. $$
は\(x=2\)で連続か。
実際にグラフを描いてみると、このようになっています。
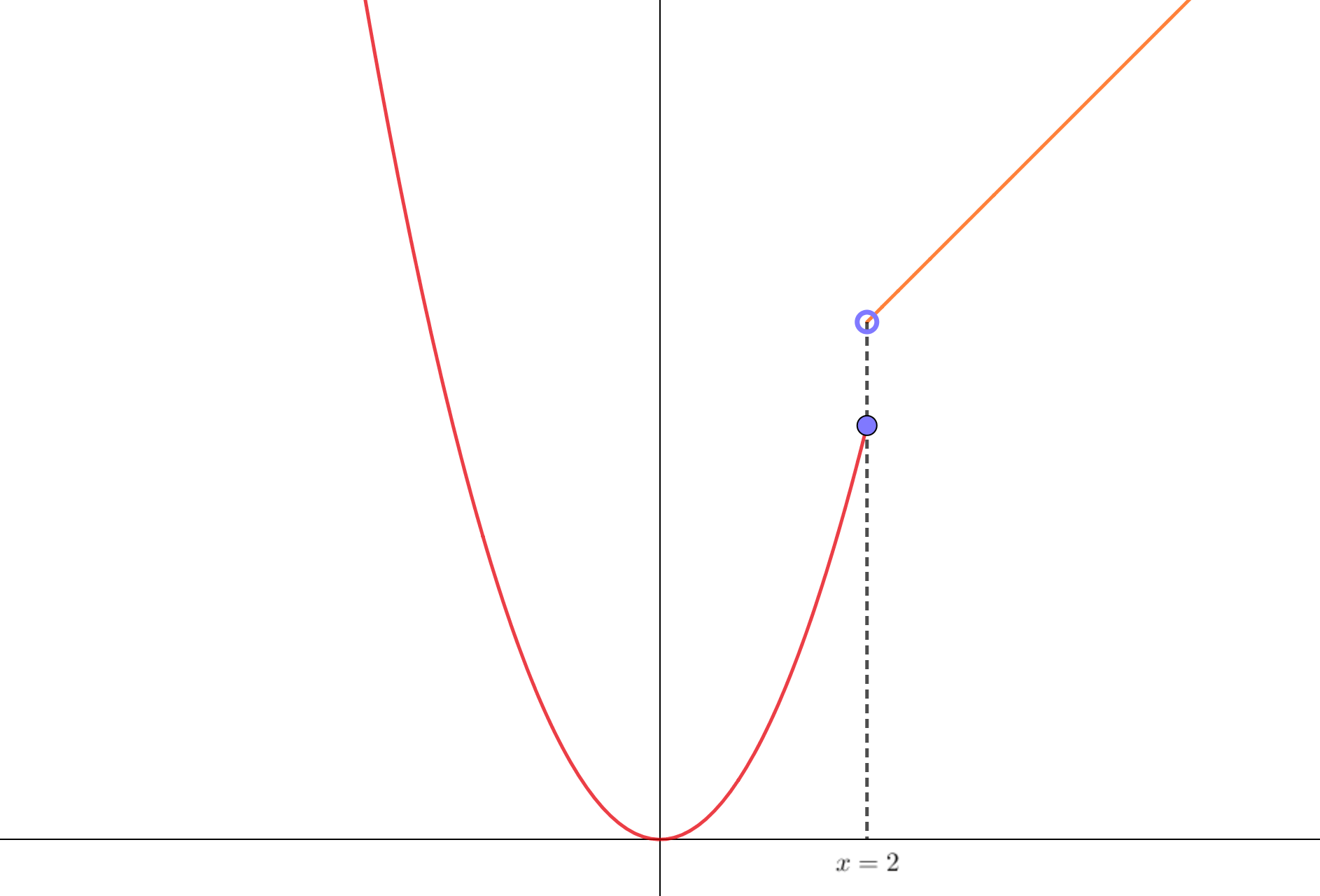

この関数は\(x=2\)のとき、\(y=x^2=4\)という値が求まります。
そのため式だけ見ると、\(x=2\)のときでも連続だと考えられます。
ところが、
かつ、
となっているため、右極限と左極限が一致しません。
つまり、(図を見てもわかる通り)明らかに連続ではありません。

「この関数、この点で連続かどうか怪しいなぁ」と思ったら、図が描けなくても、その部分の右極限と左極限が一致するかを調べれば良い。
まとめ

まとめ
- 右極限を$$\lim_{x \to a+0}f(x)$$と表し、左極限を$$\lim_{x \to a+0}f(x)$$と表す。
- 右極限と左極限の値が\(x=a\)で一致したとき、$$\lim_{x \to \color{red}{a}}f(x)=f(a)$$と表し、関数\(f(x)\)は\(x=a\)で連続であるという。
- 連続でないことを示すには、右極限と左極限が異なることを示せばいい。
連続は、微分や積分でかなり重要なポイントになります。
しっかり理解しておきましょう!
以上、「連続って何?」についてでした。








