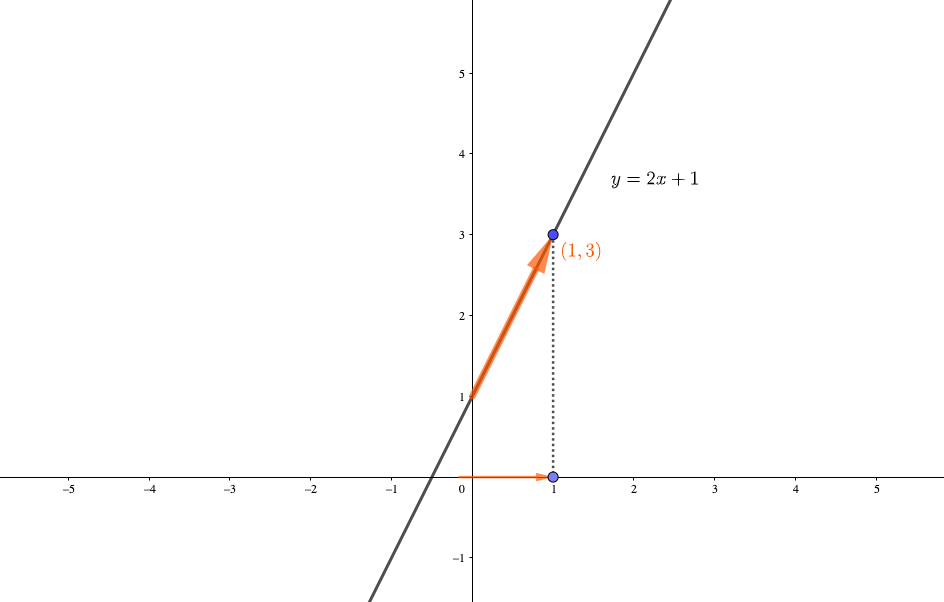Today's Topic
関数の極限値を考えるためには、
- 左極限・右極限を考え、
- それぞれの極限値が一致するかを調べれば良い。



この記事を読むと、この意味がわかる!
- 関数の極限の特徴
- 数列の極限との違い

関数の極限
数列の極限では、無限数列\(\{a_n\}\)に対して、項\(n\)をどんどん大きくしていき、\(n\to\infty\)の場合を考えましたね。
もし\(n\)が大きくなるほど、ある値\(\alpha\)に近づいていくなら、その値を極限値と呼び、数列\(\{a_n\}\)は収束するというのでした。

関数の極限は、基本的に数列の極限と同様です。
ある関数\(y=2x+1\)についてみてみましょう。
\(x\)の値を限りなく1に近づけていくと、\(y\)の値は限りなく3に近づくことが分かりますね。
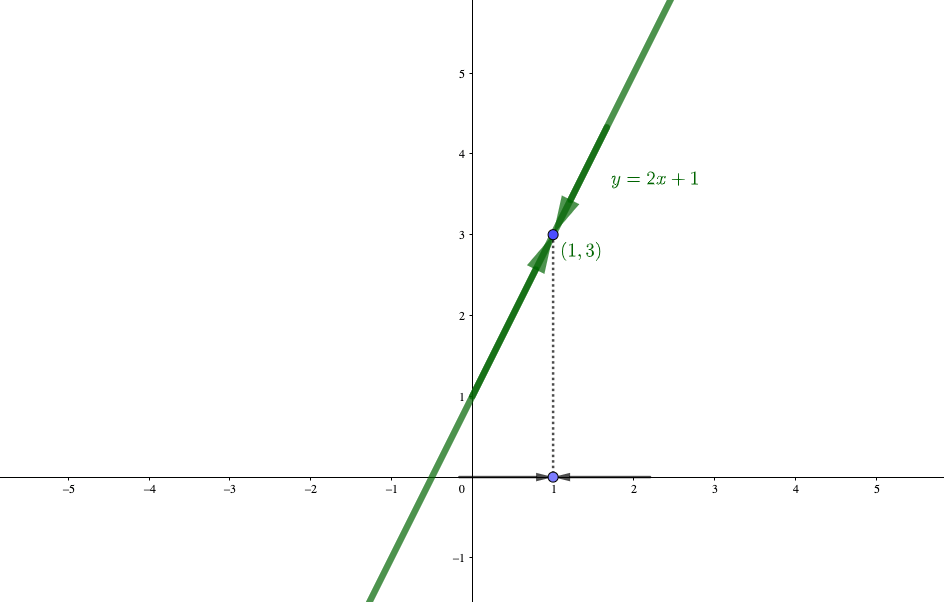
このような場合、
と表します。
【ここが大事】右極限・左極限

さて、関数の極限ですが、既に数列の極限とは違うポイントがあります。
まず数列の極限では\(n\to\infty\)のみを考えてきましたが、関数の極限では\(x\to\infty\)のみならず、\(x\to3,\ x\to -2\)など様々な値に近づく場合を考えます。
そして最も大きなポイントなのが、近づけ方が異なるという点です。

数列の極限では、\(n\to\infty\)のように項が一方的に増える場合のみを考えてきました。
しかし関数の極限では、\(x\)を3に近づけるということを考える際、
- \(x\)が1よりも値が小さい地点から、一方的に値が増加して(左から)3に近づく場合

- \(x\)が1よりも値が大きい地点から、一方的に値が減少して(右から)3に近づく場合

の2通りが考えられます。
視覚的に捉えると、
- 左からの極限
- 右からの極限
を考えている、ということになりますね。
関数の極限では、それぞれ左極限、右極限といい、先ほどの例をもとにすると、極限値は次のように表されます。
ポイント
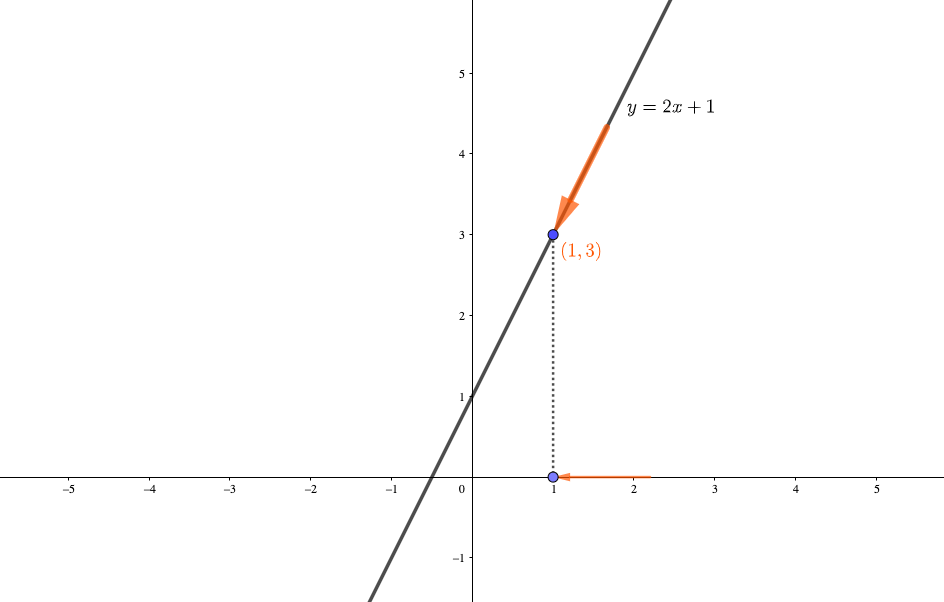
- 【左極限】
\(x\)が1よりも小さい値を取りながら、限りなく1に近づくとき、\(f(x)=2x+1\)は限りなく3に近づく。これを$$\lim_{x\to 1\color{red}{-0}}(2x+1)=3$$と表す。
- 【右極限】
\(x\)が1よりも大きい値を取りながら、限りなく1に近づくとき、\(f(x)=2x+1\)は限りなく3に近づく。これを$$\lim_{x\to 1\color{red}{+0}}(2x+1)=3$$と表す。
【ポイント】関数の極限の定義
関数の極限は、この左極限・右極限を用いて、次のように定義します。
定義
関数\(y=f(x)\)が\(x=a\)において、
- 左極限\(f(x) \underset{x\to a-0}{\longrightarrow} \alpha\)
- 右極限\(f(x) \underset{x\to a+0}{\longrightarrow} \beta\)
となるとき、\(\alpha = \beta\)であれば関数\(f(x)\)の極限値は\(\alpha\)であると定義する。

具体的に考えてみましょう。
極限値を定義できる場合
例題
関数\(y=2x+1\)の\(x=1\)における極限値を求めよ。
この例では、グラフを考えると
- 左極限\(y \underset{x\to 1-0}{\longrightarrow} 3\)
- 右極限\(y \underset{x\to 1+0}{\longrightarrow} 3\)
となりますね。
よって左極限と右極限の値が一致するので、極限値を考えることができ、その値は3ということになります。
これを
と表しますが、\(x\to 1\)は\(x\to 1-0\)のときと、\(x\to 1+0\)のときの極限値が一致しないと表記できないことに注意しましょう。
極限値を定義できない場合
例題
$$関数f(x)=\left\{ \begin{array}{l} x-2\ (x<3) \\ -(x-3)^2+4\ (3<x) \end{array} \right. $$
この例では、グラフを考えると
- 左極限\(y \underset{x\to 3-0}{\longrightarrow} 1\)
- 右極限\(y \underset{x\to 3+0}{\longrightarrow} 4\)
となりますね。
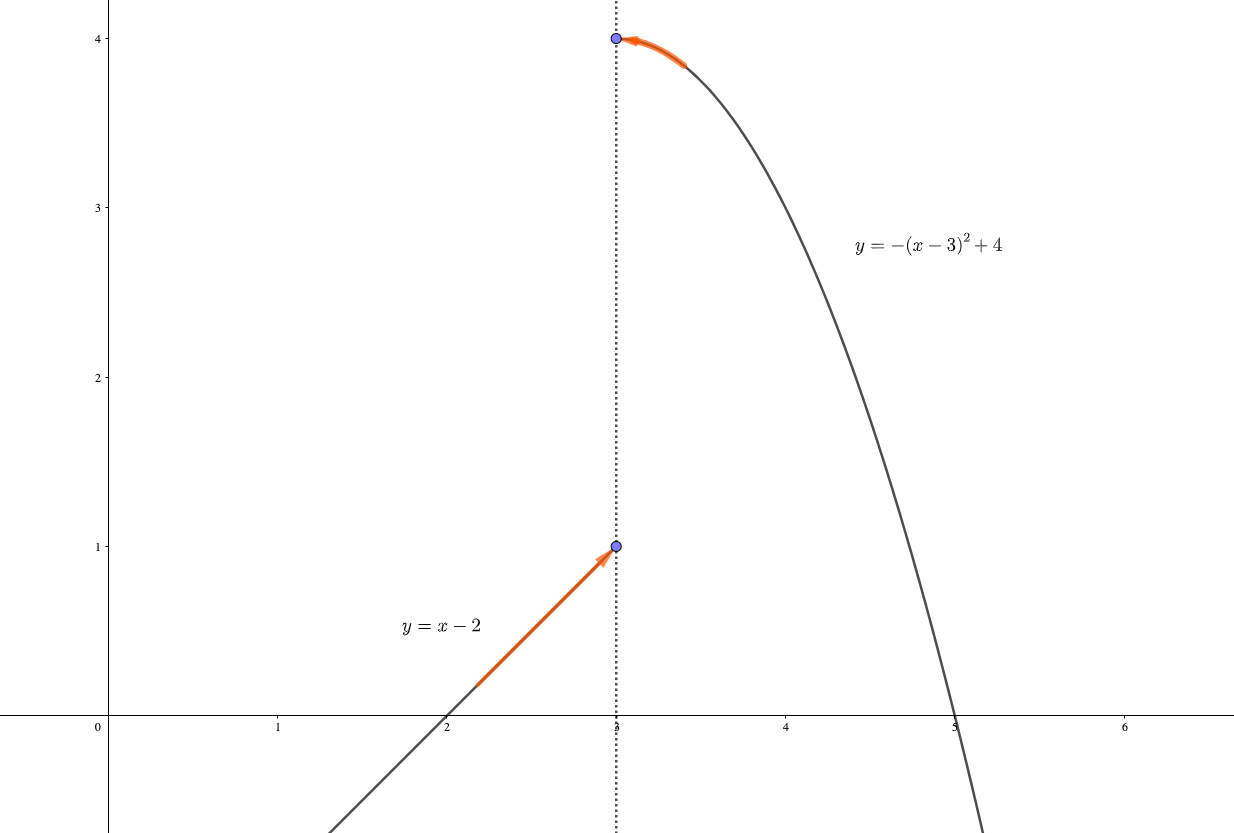
左極限と右極限の値が一致しないので、この場合は\(f(x)\)の極限値は存在しないということになります。
まとめ

まとめ
関数の極限値を考えるためには、
- 左極限・右極限を考え、
- それぞれの極限値が一致するかを調べれば良い。
既にお分かりかもしれませんが、関数の極限にはグラフ力がかなり重要になります。
数列の極限のコツでも、ちょこちょこグラフを用いて解説していたのはこのギャップをなくすため。

なかなか理解できないなと感じたら、まずはグラフを見直すところから始めてみましょう。
以上、「関数の極限について」でした。
チェック問題
例題
次の関数の\(x=0\)における極限値を調べよ。
関数\(f(x)=\frac{1}{x}\)
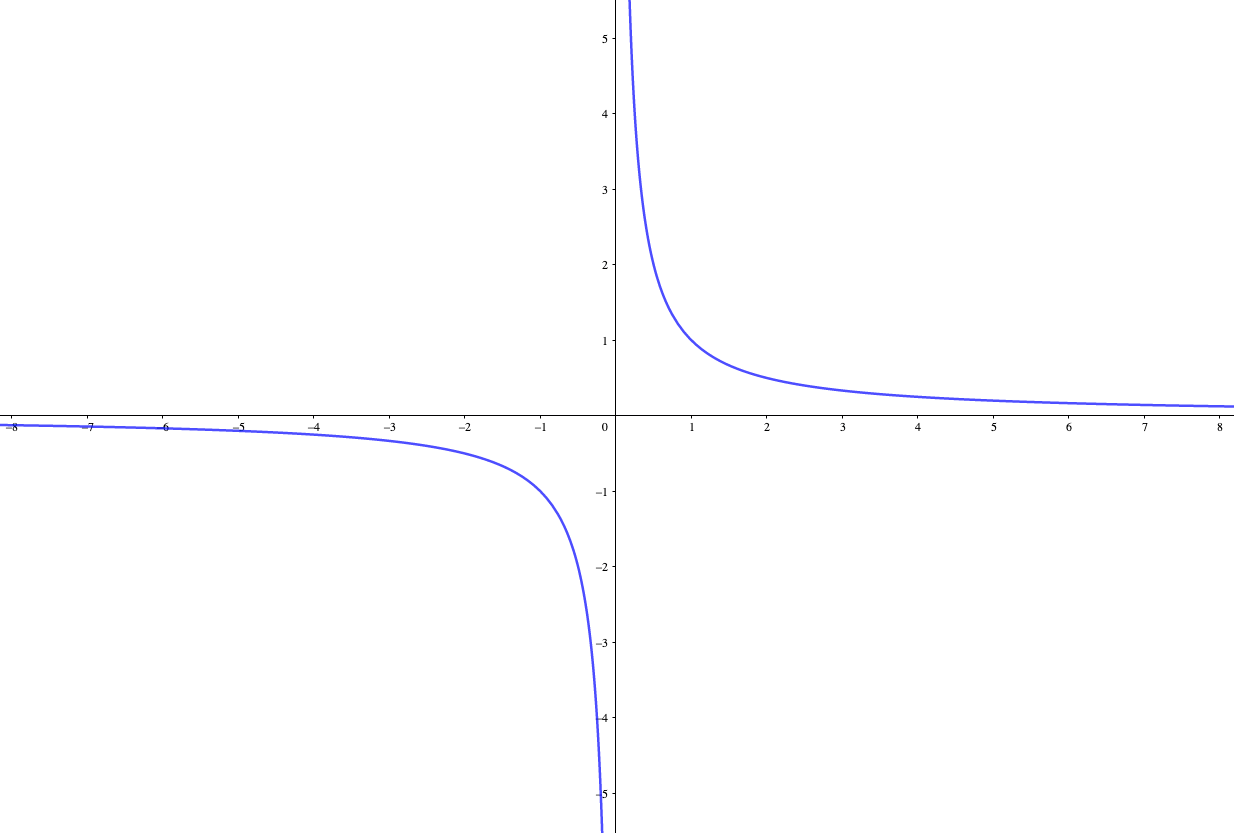
グラフより、
左極限\(f(x)\underset{x\to -0}{\longrightarrow} -\infty\)
右極限\(f(x)\underset{x\to +0}{\longrightarrow} \infty\)
例題
次の関数の\(x=0\)における極限値を調べよ。
関数\(f(x)=\frac{1}{x^2}\)
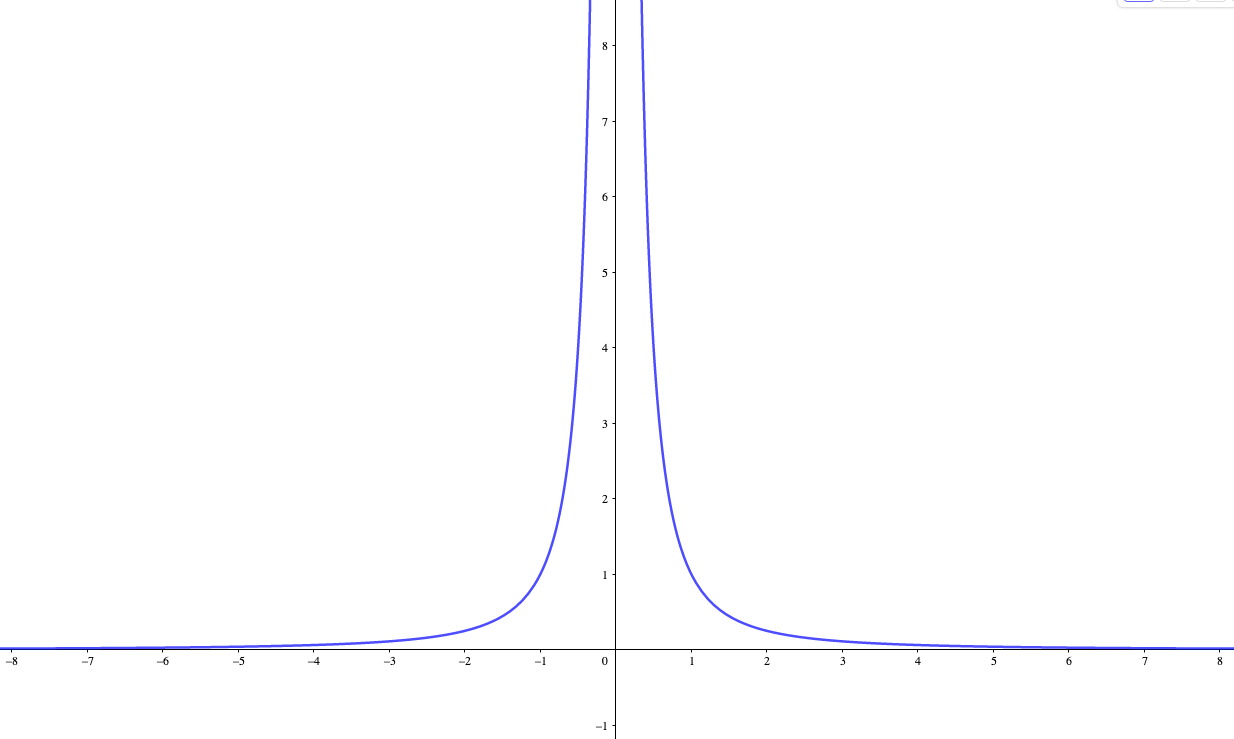
グラフより、
左極限\(f(x)\underset{x\to -0}{\longrightarrow} \infty\)
右極限\(f(x)\underset{x\to +0}{\longrightarrow} \infty\)
よって、左極限と右極限が一致する。
つまり