Today's Topic
$$0.33333\cdots,\ 1.5353535353\cdots$$
のように、同じ数字が繰り返し現れる無限小数のことを循環小数といい、これは分数で表すことができる




この記事を読むと、この問題が解ける!
次の循環小数を分数で表せ。
- $$0.657657657657\cdots$$
- $$1.37432323232\cdots$$
Contents
小数の区別
循環小数とは、
$$0.33333\cdots,\ 1.5353535353\cdots$$
のように、同じ数字が繰り返し現れる無限小数のことです。

ここで、小数の分類について復習しておきましょう。

数の集合の記事でも扱いましたが、小数には次の3種類があります。
(例)$$0.3\ ,\ 0.6453$$
【循環無限小数】・・・同じ数やパターンが繰り返しずっと出てくる小数
(例)
(※見切れている場合はスクロール)
【ランダム無限小数】・・・特にパターンのない数が羅列する小数
(例)$$3.14159\cdots\ ,\ 1.4132135\cdots$$
これら小数の、数の集合における位置づけは次のようになっています。
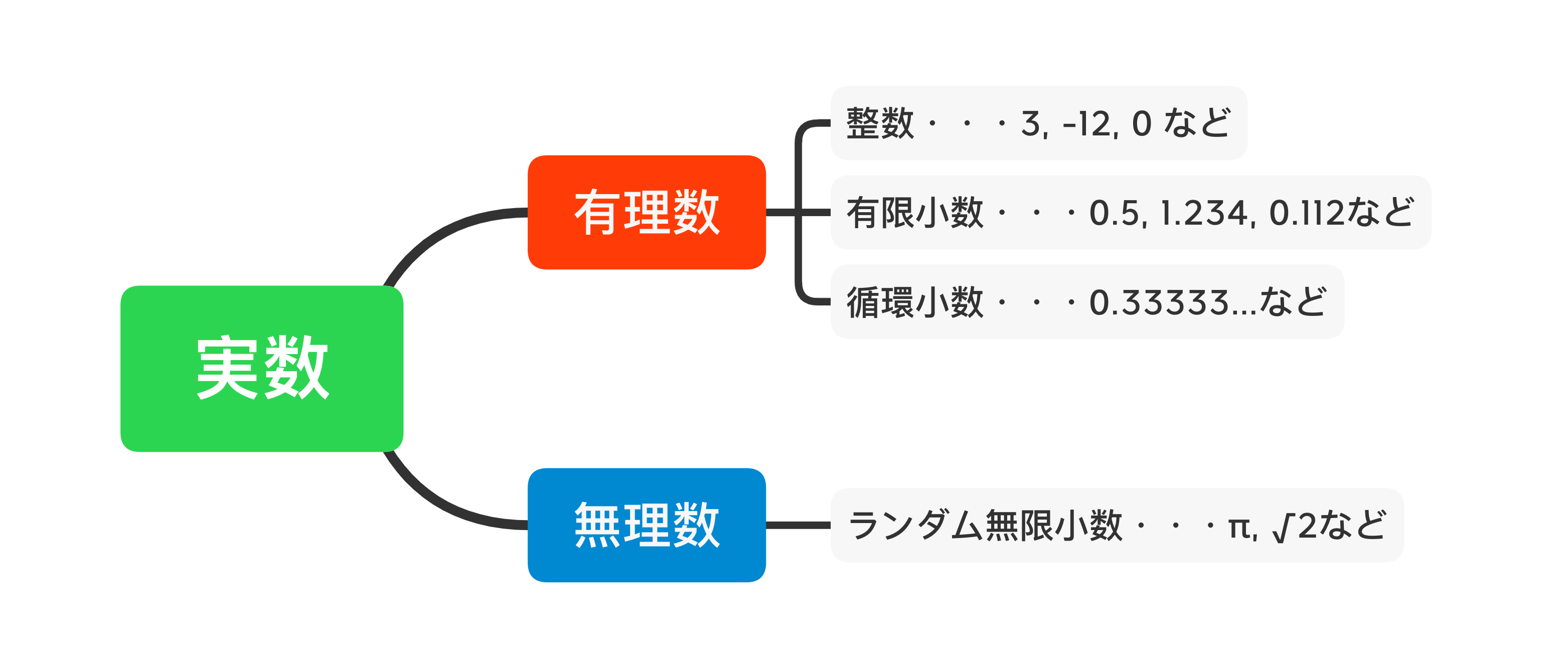
つまり循環小数は、有理数なので分数で表すことができるということです。
今回扱う内容は、その「循環小数を分数で表す」方法になります。
循環小数を分数に直す2つの方法
循環小数を分数で表す方法は
- 無限等比級数を使う
- 方程式を使う
の2種類があります。
無限等比級数を使って循環小数を分数に直す
次の循環小数を例に、分数化してみましょう。
例題
$$0.\dot{5}\dot{7} = 0.575757575\cdots$$
この小数を次のように分解します。
(※見切れている場合はスクロール)
するとこの式から、\(0.\dot{5}\dot{7}\)は初項\(0.57\)、公比\(0.01\)の無限等比級数であることがわかりました!
公比\(r\)が\( |r| < 1\)のときであれば、初項\(a\)、公比\(r\)の無限等比級数は
に収束するのでしたね。
もちろん無限等比級数\(0.\dot{5}\dot{7}\)の公比\(0.01\)は、\(|0.01| < 1\)を余裕で満たすので、
に収束する事になります。
よって、
とわかります。
方程式を使って循環小数を分数に直す
どうしても無限等比級数を使って紹介したかったので先に紹介しましたが、実は循環小数を分数に変形する方法は中学生の頃に既にやっています。

例題
$$0.\dot{5}\dot{7} = 0.575757575\cdots$$
まず
とおきましょう。
これを100倍すると、
となりますね。
この差をとると、
となるので、
となり、先ほどと同じ答えが得られます。
小数点以下がうまく消えるように、\(10^{n}\)倍してあげれば良い

ただしこの式には少し怪しいところがあります。
いくら無限に続く小数とは言え、100倍した値の小数点以下と、100倍していない数の小数点以下は綺麗に相殺するのでしょうか?
その怪しさを排した回答が無限等比級数を使った回答なので、ぜひ高校生であればそちらをマスターしていただきたいです。
【実は嘘?!】ホントに\(1 \div 3 = \frac{1}{3}\)?
さて、最後にしれっと教えられた循環小数についてみてみましょう。
割り算は分数で表すことができる、と教わりましたね?
具体的には、
と表せると教わったはずです。
左辺を計算すると、
が成り立つわけです。
でもこれは、本当に右辺と左辺がイコールで結べるものなのでしょうか?


等式の性質より、右辺を3倍したとき、左辺も3倍されなければなりませんね。
よって、上記の等式が成り立つならば、
が成り立たなければなりません。
これを計算してみると。。。

これが小学校で習ったちょっとしたウソ。
違う数は等しくなることは、本当はあり得ません。
しかし、無限等比級数の考え方を使うと、
(※見切れている場合はスクロール)
となるため、高校数学で習う無限等比級数を用いればウソでないと示せるわけです。


まとめ

まとめ
循環小数を分数で表すためには、
- 初項\(a\)、公比\(\frac{1}{10}^{n}\)の無限等比級数であることを確認し、
- 公比が1よりも小さい無限等比級数は\(\frac{初項}{1-公比}\)に収束する事に着目して、
- \(\frac{a}{1-\frac{1}{10}^{n}}\)を求めれば良い。
小学校から当たり前のように習っていた分数。
実はその裏に、高校数学の極限で扱われる無限の考え方がしれっと隠れていたんですね。
無限等比級数の考え方を利用して、ぜひ循環小数を分数に治せるようになっておきましょう。
以上、「循環小数の求め方と分数のウソ」についてでした。
チェック問題
例題
次の循環小数を分数で表せ。
- \(0.657657657657\cdots\)
- \(1.37432323232\cdots\)
難しくないので一気に解きます。
(※見切れている場合はスクロール)
よって、初項\(0.657\)、公比\(\frac{1}{1000} < 1\)の無限等比級数より、その値は
となります。
2番目も同様にやります。
(※見切れている場合はスクロール)
\(1.374\)以降の式は、初項\(0.00032\)、公比\(\frac{1}{100} < 1\)の無限等比級数なので、答えは
となります。








