【指数関数のグラフと性質】これだけはサッと思い出したい、超重要な6つの性質

楓

今日は指数関数のグラフを眺めていくよ！

指数関数って、なんかグニ〜ンって曲がるやつだよね？

小春

楓

そう笑 どうしてあの形になるのかは置いといて、その形からどのような性質があるかを押さえていくよ！

この記事を読むと、この問題が秒で解ける！

• \(x=3.453\)のとき、次の中で最も小さくなる数はどれか
  $$\left(\frac{14}{13}\right)^x -1, \ \left(\frac{21}{17}\right)^x -1, \ \left(\frac{24}{15}\right)^x -1, \ $$

  （※見切れている場合はスクロール）

• \(t=2^x\)とする。このとき、\((t+1)(t-4)=0\)を満たす\(x\)の値を求めよ。

楓

解答は一番最後に見ていくよっ！

指数関数のグラフ

\(y = 2^x\)や\(y=\left(\frac{1}{3}\right)^x\)のように表される関数を指数関数といいます。

明確な定義は次のとおりです。

注意して欲しいのは、この定義では\(a\)の値が負のときや、0、1になるときは考えないことが前提になっています。

参考【指数関数の定義】なぜ底が負のときは定義しないのか→ダルいから

この定義を念頭に置いた上で、例えば指数関数\(y=2^x\)のグラフは次のようになります。

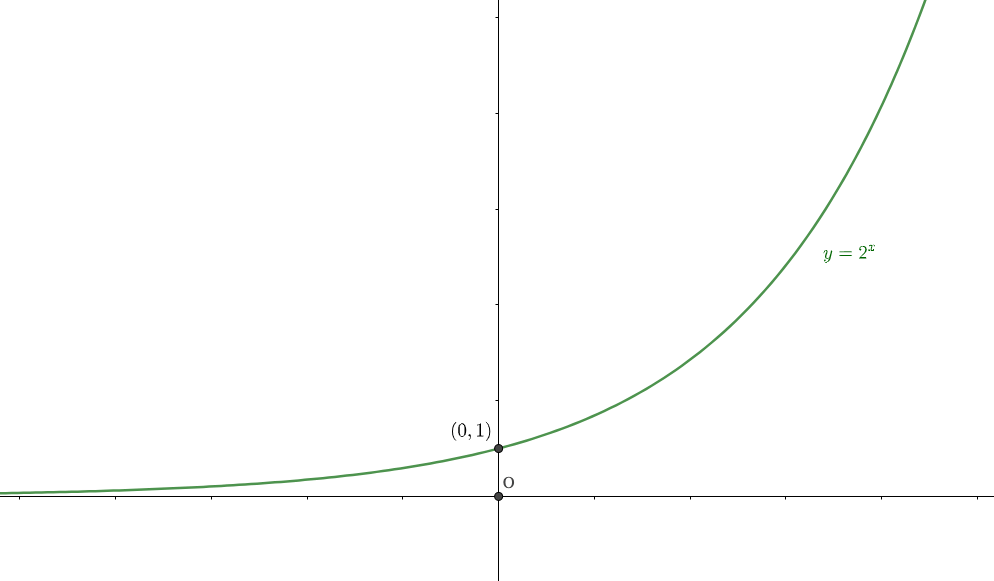
\(y=2^x\)のような

を満たす指数関数を、『指数関数のベース』として捉えておきましょう。

そうすることで、グッと理解がしやすくなります。

小春

どんな指数関数も、この指数関数をもとにしているってことね！

指数関数のグラフの特徴

それでは指数関数の特徴を1つずつ見ていくことにしましょう。

ここでは具体例として、\(y=2^x\)を見ていきましょう。

\(x\)の値の変化によって、\(y\)の値が急増、緩減すること

指数関数\(y=2^x\)をはじめとする、指数関数のベースはみな、\(x\)の値が大きくなるほど\(y\)の値が大きくなり、\(x\)の値が小さくなるほど\(y\)の値も0に近づいています。

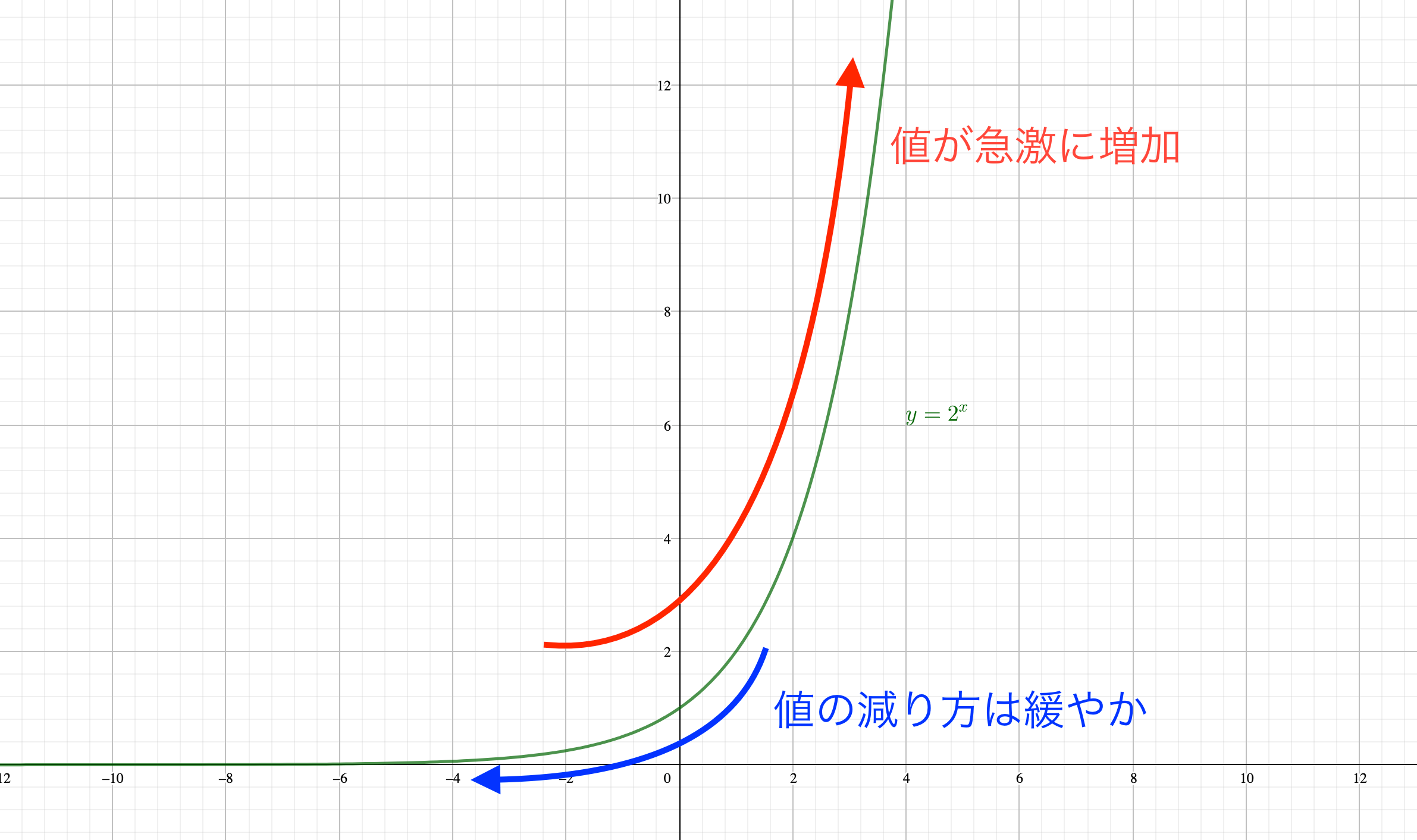
グラフの形で特徴的なのは、\(y\)の値の増え方はグニ〜ンと急激に増加しているのに対して、\(y\)の値の減り方はかなり緩やかです。

例えば\(y=2^x\)において、\(x=3\)のときは\(y=2^3=8\)なのに対して、\(x=4\)のときは\(y=2^4=16\)と、\(x\)の値は1しか違わないのに値は2倍になっていきます。

対して、\(x=-2\)のときは\(y=2^{-2}=\frac{1}{4}\)、\(x=-3\)のときは\(y=2^{-3}=\frac{1}{8}\)と、その差は0.125しか違いません。

小春

計算すれば当たり前じゃ・・・

そうだね。ちなみにこの急増の仕方が特徴的すぎて、「指数関数的に増大」ってワードも生まれてる。意味は急成長ってことね！

楓

0以下にならない

グラフを見てみると、\(x\)の値が減るに従って、\(y\)の値がどんどん0に近づいていることがわかります。

コンピュータで書いたグラフでは、あたかも\(y=0\)、つまり\(x\)軸に触れているように見えますが、指数関数のベースは絶対に\(x\)軸とは接触しません。

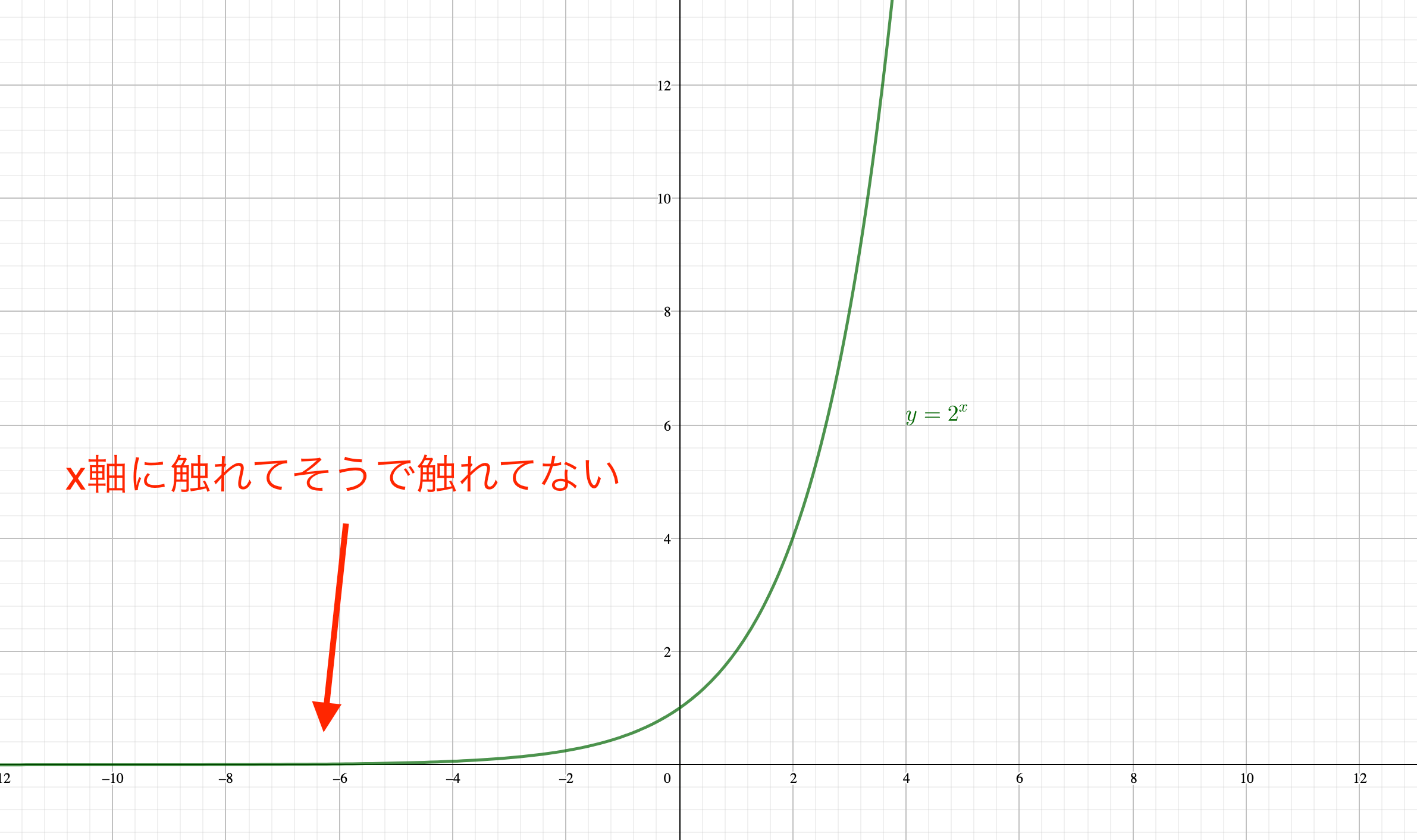
これは指数について考えてみれば当然ですが、\(y=2^x\)の\(x\)にどんな値を代入しても、\(y\)の値を0にすることはできませんよね？

ちなみに指数関数は、\(x\)の値が大きなるほど、\(y\)の値は無限大に増加します。

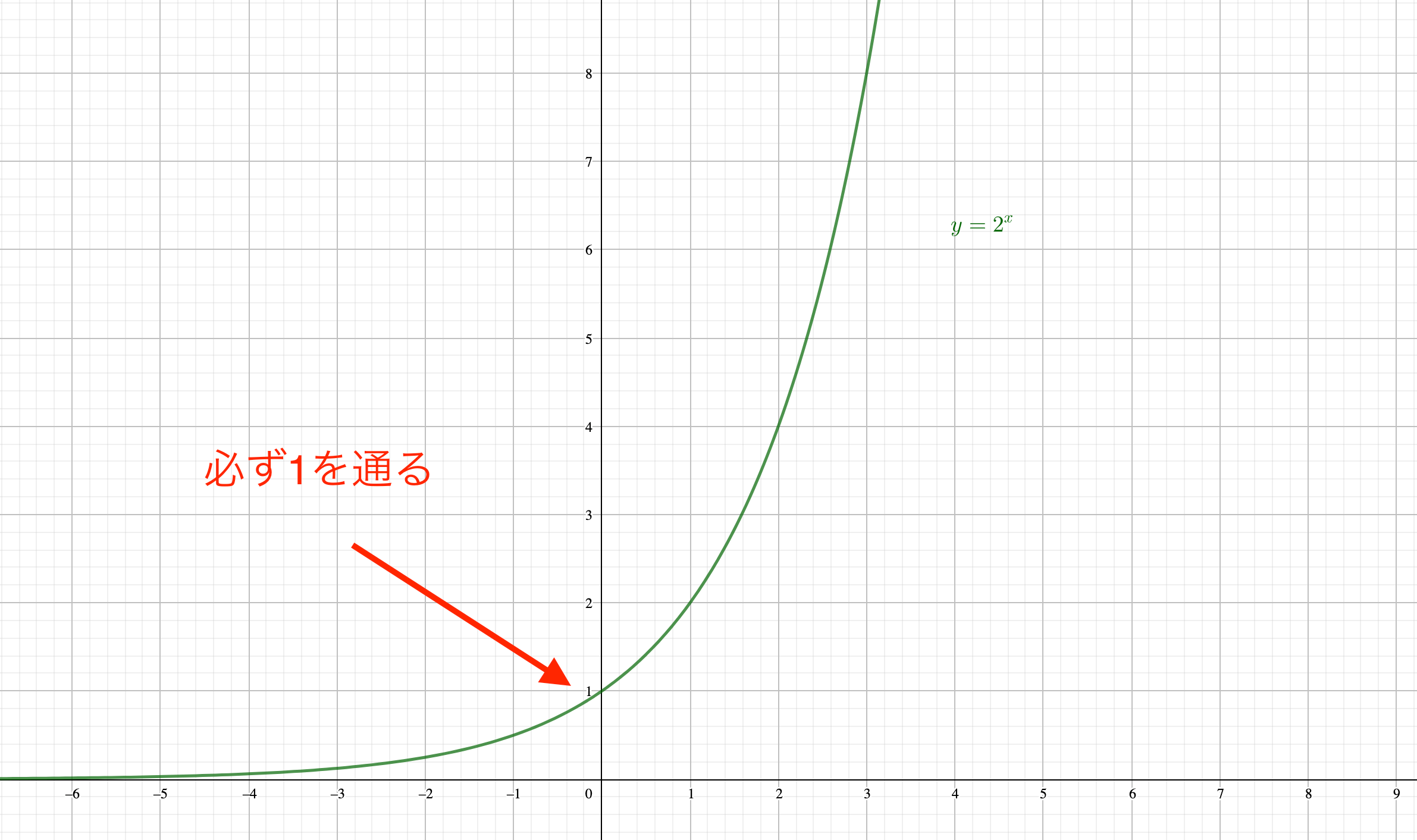
必ず1を通ること

指数法則では、0乗のときに結果をもれなく1にすることを定義としました。

参考【整数の指数法則】なぜ0乗が1なのか、息をするようにわかる指数法則

指数関数の\(x\)の値は実数なので、当然0を取ることにもなります。

よって、\(x=0\)のときにベースの指数関数は必ず\(y=0\)となることが決まります。

底が逆数になると\(y\)軸対象になること

指数関数のベース、例えば\(y=2^x\)における数2のことを『底』といいますが、この底が逆数になった指数関数\(y = \left(\frac{1}{2}\right)^x\)のグラフを見てみましょう。

小春

反転した！？

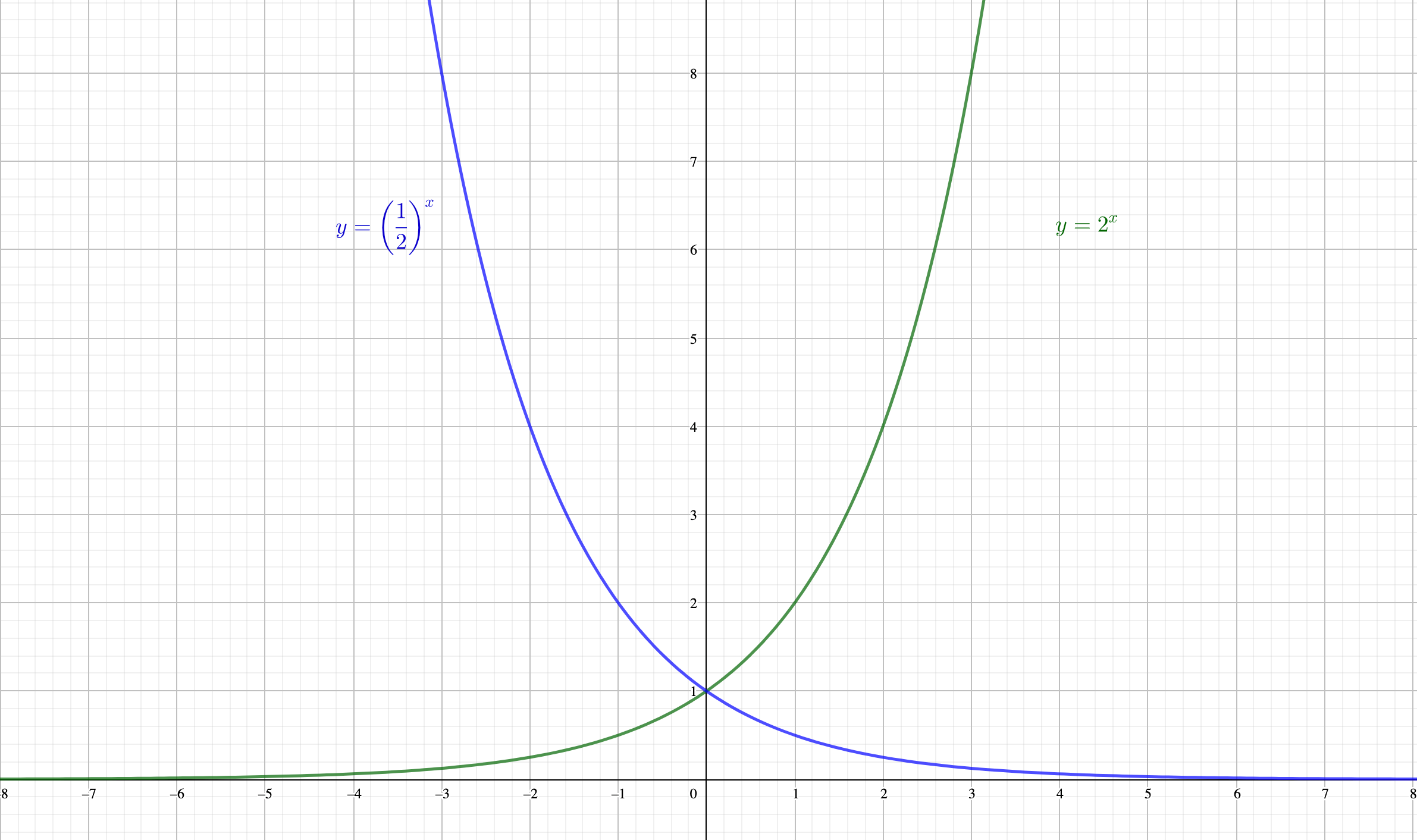
このように底が逆数になると、グラフは\(y=1\)を通りながらも、\(y\)軸に対して線対称となります。

底が大きくなるほど\(y\)軸寄りに、小さくなるほど直線\(y=1\)に近づく

では、この指数関数のベース\(y=a^x\)は底\(a\)によって、どのような振る舞いをするのかみてみましょう。

まずは底が1よりも大きい場合を見てみましょう。

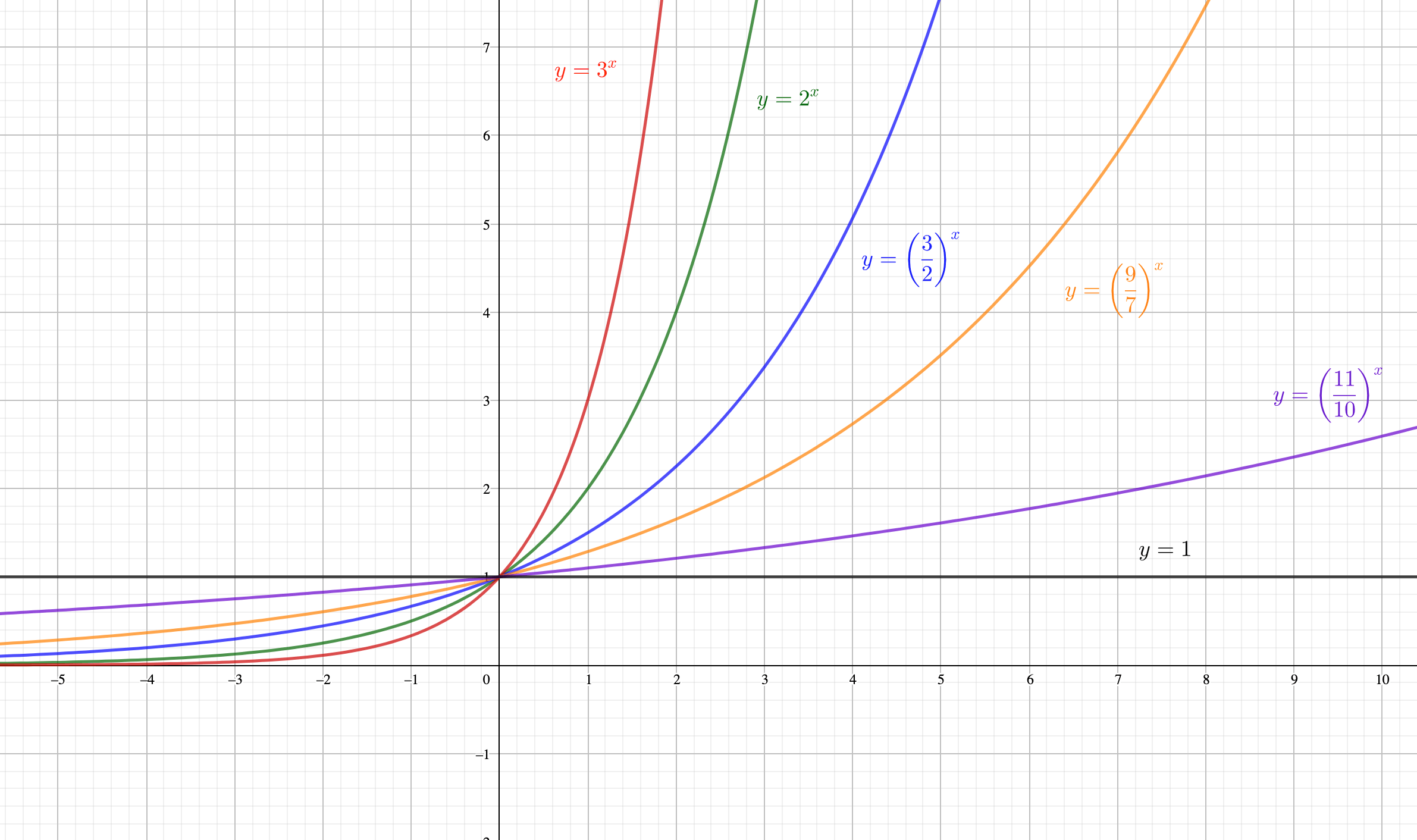
ちょっとカラフルにしすぎたかもしれませんが、底が1よりも大きいときは底が小さくなるほど\(y=1\)に近づいていることがわかります。

では底が1よりも小さいときはどうなるか、実はもう予想できているのではないでしょうか？

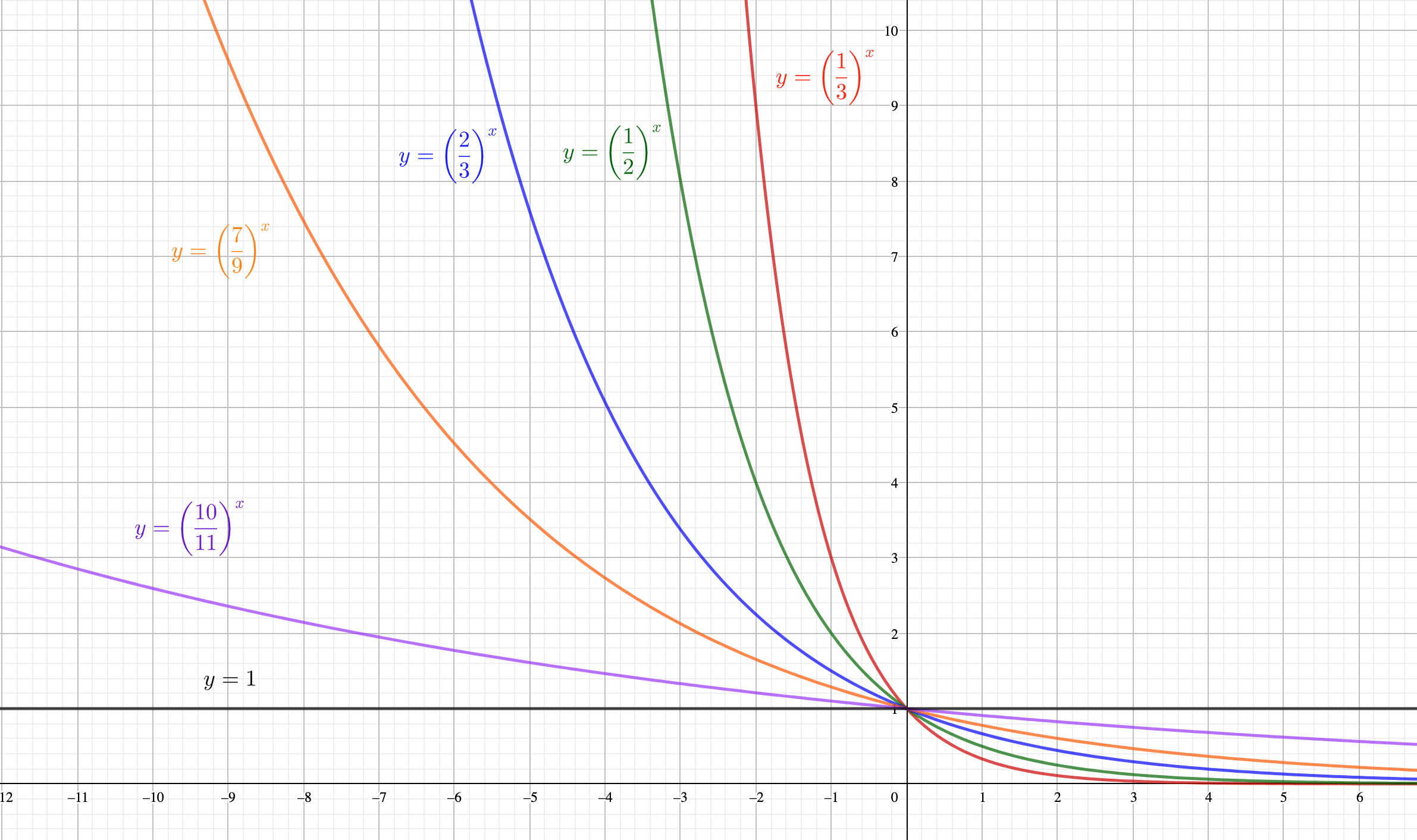
底が逆数になると、グラフは\(y\)軸対称になるのでした。

つまり、底が1よりも小さいときは底が大きくなるほど\(y=1\)に近づいていることが、（あまりグラフを見なくても）わかるはずです。

対数関数と\(y=x\)において線対称であること

対数関数\(y=\log_2 x\)のグラフを見てみましょう。

小春

\(y=x\)をつまんで、くるって回したみたい・・・

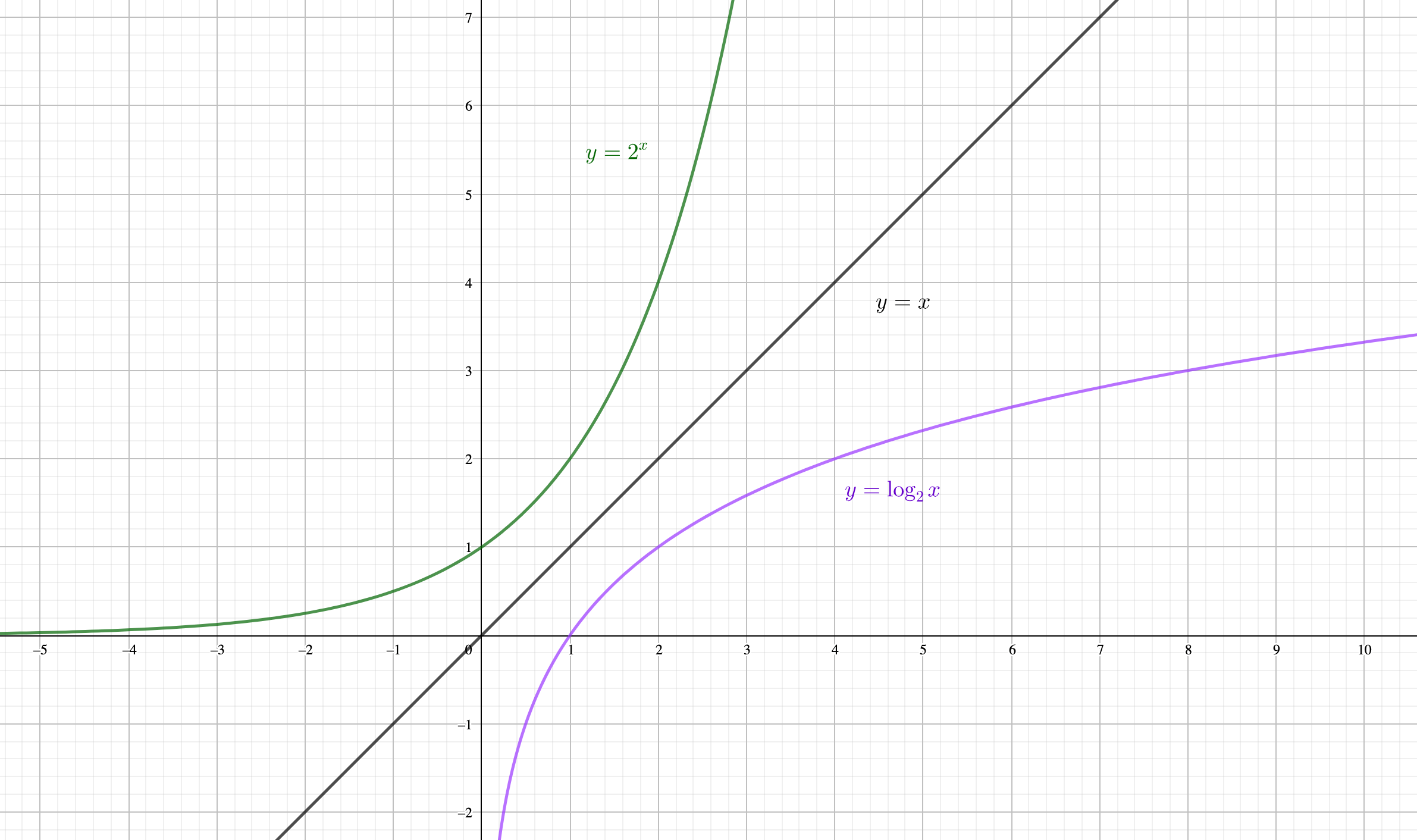
このように指数関数のベース\(y=a^x\)に対して、対数関数\(y=\log_a x\)は\(y=x\)に対して対称的なグラフになります。

結果だけ抑えておけばいいですが、理由も説明しておきましょう。

対数\(y=\log_a x\)は、日本語に翻訳すると「\(x\)は\(a\)の\(y\)乗」です。

楓

具体的に\(\log_2 8 = 3\)を思い出すといいよ。8は2の3乗だよね？

参考log(ログ)って何？常用対数、自然対数とは？対数を徹底解説！！

つまり、対数関数\(y=\log_a x\)は指数関数\(x = a^y\)と同じ意味になります。

2つの指数関数\(y=a^x\)と\(x=a^y\)は\(x\)と\(y\)を入れ替えただけの関係になりますね。

この関係を逆関数といい、逆関数には\(y=x\)に対して線対称になるという性質があります。

参考逆関数とは？グラフから考える『入れ替える』意味とその性質

つまり指数関数と対数関数には、逆関数という関係があり、それがこの\(y=x\)に対して対称となる理由になっているんですね。

グラフの特徴だけで問題の罠やゴールが見える

今回はグラフの形を眺めてみて、さっとわかる特徴を言語化していきました。

小春

「え、これみたまんまじゃん。なにに役立つの？」

というのは率直な感想でしょう。

ではグラフの特徴をしっかり理解しておくと、どれだけ便利か、練習問題を見てみましょう。

小春

ひぃえぇ〜、3乗根もあるし小数もあるし不気味だよぅ〜泣

一見不気味ですが、これらの指数は全て底を2、もしくは4で揃えることができます。

例えば4で揃えてみると

のようになります。

底が1より大きいとき、指数関数は\(x\)の値が大きいほど、その値が急増するのでした。

そのため結局、指数の大小関係だけをみればよく、

であることから、

の順になるため、

とわかります。

この解答で特殊なのは、底を4で揃えるという発想です。

計算機で計算するわけでもなく、なぜ底を4で揃えるという発想が出てきたのか、それは指数関数のグラフの振る舞いを解法に応用したためです。

計算機を用意しなくても、指数関数のグラフの性質を考えると、底さえ揃えることができれば指数の大小比較に持ち込める、という流れなんですね。

まとめ

楓

それじゃまとめるよ！

指数関数の性質は、結構な問題で解法の1手として登場します。

先ほどの例題は、もちろん一例に過ぎず、まだまだいろんな性質を利用した解法があります。

いつか、「当たり前やろ」といって解けるようになるといいですね。

もちろん、6つの性質を丸暗記する必要はなく、グラフを紙の隅っこに書いて考えてみてもOKです。

振る舞いから解法の流れを捉えられるようにしていきましょう！

以上、「指数関数のグラフとその振る舞いについて」でした。

チェック問題

先ほど扱った例題では底を4に揃えることで、実質的に指数の比較に持ち込みました。

しかし今回は底を揃えることは厳しそうです。

そこで底をじっくり観察してみると、どれも1よりも大きいことに気づきます。

底が1よりも大きい場合、指数関数は底が大きいほど\(y\)軸に、小さいほど\(y=1\)に近づくのでしたね！

よって、底を比較してみると

となります。

よって、この中で最も小さい\(\frac{14}{13}\)が最も1に近いとわかります。

それはすなわち、\(\left(\frac{14}{13}\right)^x -1\)が最も小さいことを意味していますね。

小春

あれっ、\(x=3.453\)って数は使わないの！？

うん、だって解けたし。

楓

小春

えぇ、じゃあただのひっかけぇ・・・？

そうだね。僕が先生ならひっかけでこれ出すね。戦意喪失させて・・・

楓

小春

性格悪いよ

これは後に出てくる指数方程式をちょっと優しくしたもの。

普通に考えると\(t= -1, 4\)なので、\(2^x = -1, 4\)の解を探してしまいたくなります。

しかし指数関数のグラフを思い浮かべてみると、グラフは必ず\(y>0\)となるのでしたね。

よって\(2^x = -1\)の解は存在しないと一発で見抜けます。

なので、この問題を見た瞬間に\(t=4\)となる解、すなわち\(x=2\)が答えだと瞬殺できるわけですね。

指数方程式ではよく使う考え方なので、しっかり抑えておきましょう！