場合分けのコツや、場合分けが必要な場面を見極めるコツを徹底解説【二次関数で学ぶ】

小春

場合分けってなんか苦手。。。どんな風に分ければいいのかわかんない。

場合分けは「値が切り替わるポイント」で行うといいんだよ。

楓

小春

「値が切り替わるポイント」？

このポイントは二次関数を元に考えると、非常にわかりやすいよ！

楓

小春

じゃあ今日は、場合分けのポイントについて教えて欲しいな！

こちらもぜひ！

二次関数で学ぶ場合分け｜二次関数の性質

楓

まずは二次関数について復習しておこう！

中学校の時に習った二次関数のベースである\(y=ax^2\)。

この二次関数が描く放物線を

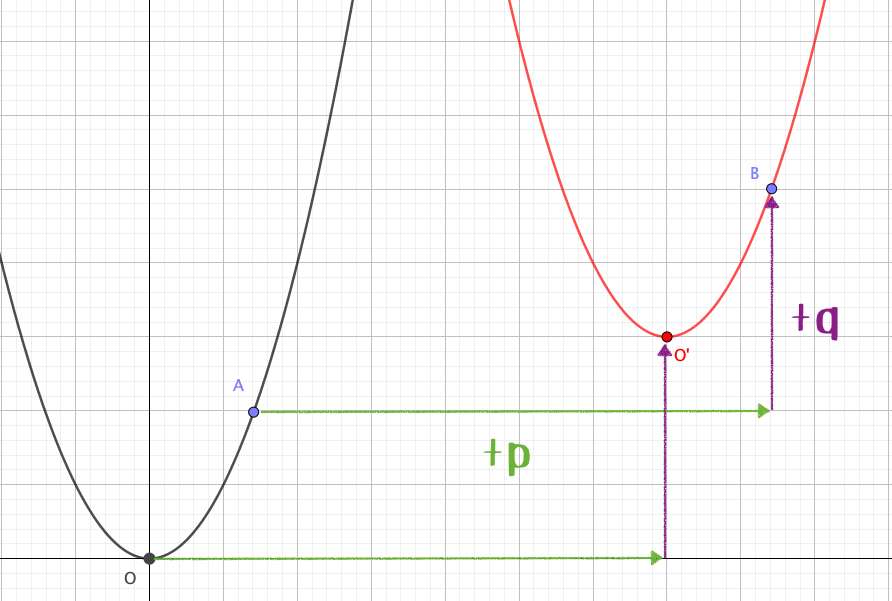
• \(x\)軸方向に\(+p\)
• \(y\)軸方向に\(+q\)

だけ平行移動したとき、その放物線の方程式は\(y-q=a(x-p)^2\)と表せるのでした。

二次関数と平方完成について復習したい人はこちらを参考にしてください。

グラフを見てもらえばわかる通り、二次関数の描く放物線は線対称になっている面白い形をしています。なお、線対称の対称軸となっている\(x=0\)（\(y\)軸）と\(x=p\)は放物線の軸と呼ばれます。

二次関数において場合分けが必要な理由は、この放物線という形に原因があります。

下の図を見てください。

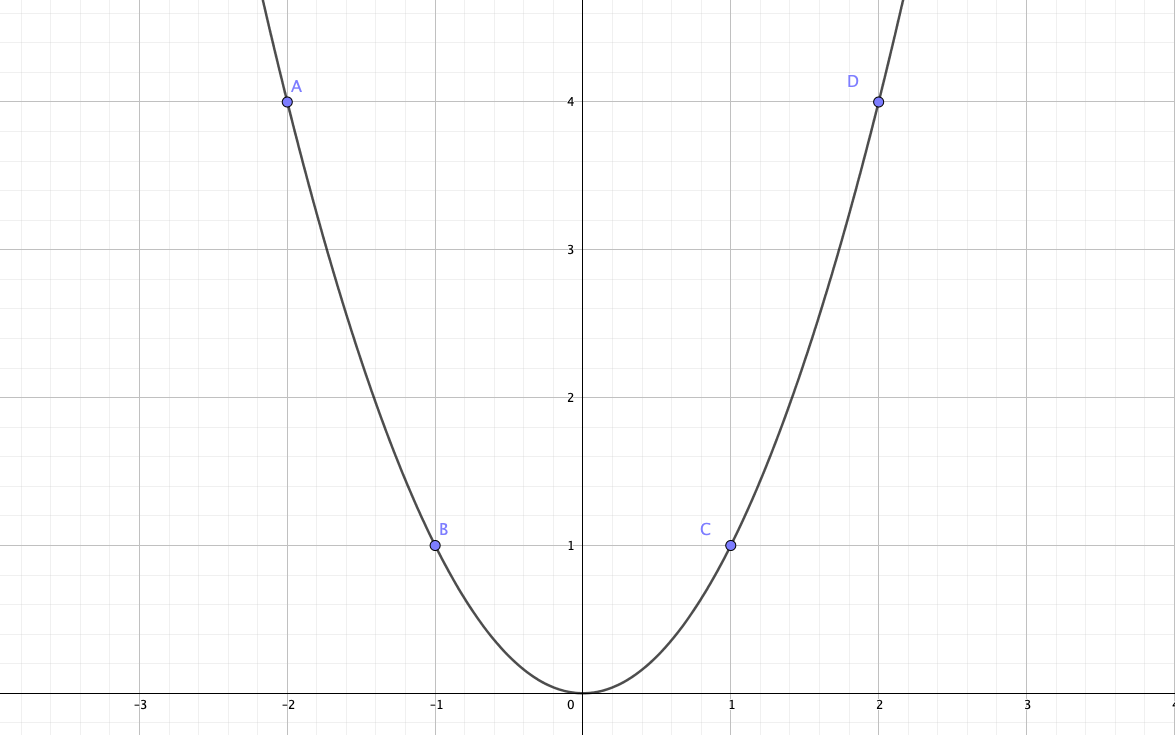
このグラフにおいて、高さが最も低い点は間違いなく原点\(O(0,0)\)でしょう。

しかし、高さが最も高い点は、この放物線がどこまでも続くので、一生求められません。

楓

放物線の先端ほど、高さが高くなっていくからね。

ところが、例えば\(-2≦x≦-1\)の範囲に限定して、グラフを見てみるとどうでしょう。

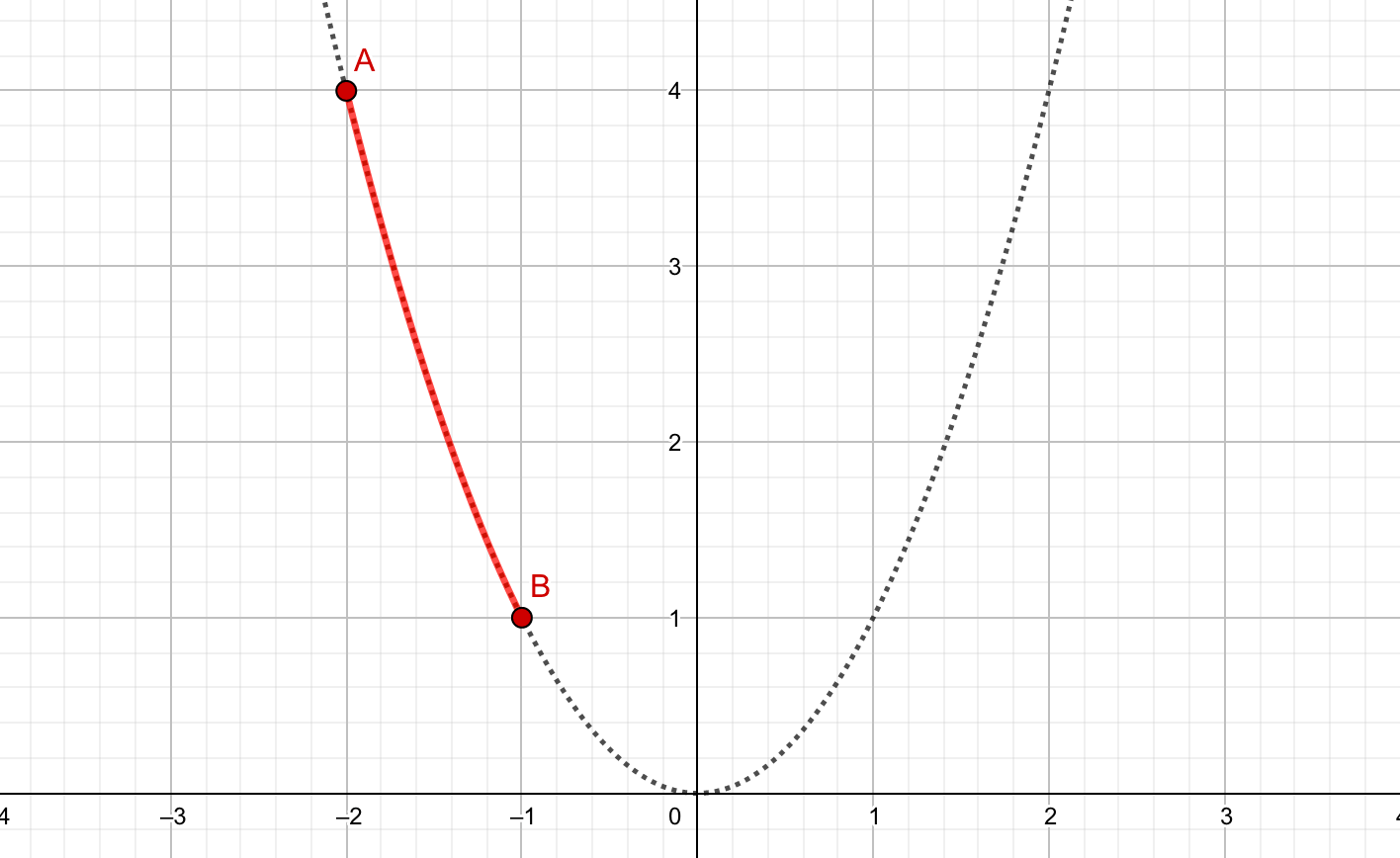
高さが最も高い点は\(A(-2,4)\)で、最も低い点は\(B(-1,1)\)となります。

では範囲を変えて、\(-1≦x≦1\)のときはどうでしょうか。

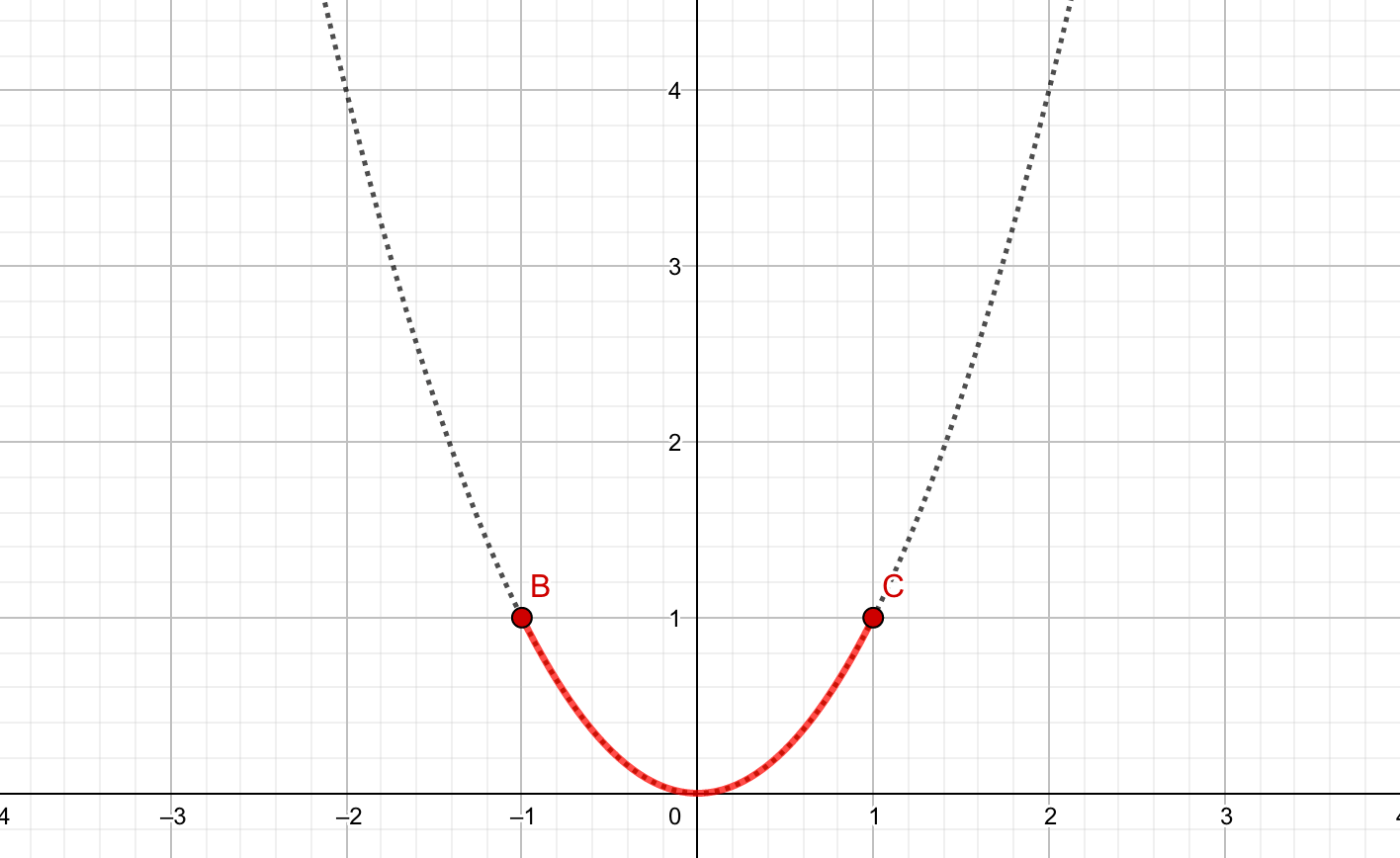
高さが最も高い点は\(B(-1,1),C(1,1)\)で、最も低い点は\(O(0,0)\)となります。

小春

さっきは最低点だった点Bが、今度は最高点になったね！？

このように、いくつかの条件が考えられて、その条件によって答えが異なる場合に場合分けが必要となります。

その理由は簡単、一気に答えを求められないためです。

楓

このグラフで最も高さが低い点は原点だ！

という意見は一見正しいようにも聞こえますが、\(-2≦x≦-1\)の範囲では不正解ですよね。

二次関数で学ぶ場合分け｜最大値最小値が変わる場面

楓

ではこれから、場合分けが必要な二次関数の具体的な問題を見ていこう！

先ほど、

\(x\)の範囲によって、\(y\)の最大値と最小値が異なるため場合分けが必要

と説明しました。

定義域の幅だったり、場所によって\(y\)の最大値・最小値は確かに異なりますね。

楓

長さが1の\(x\)の範囲が動いて、赤い点が最大値、緑の点は最小値を表しているよ。

確かに最大値と最小値が変化しているのがわかるね。

小春

ちなみに

といいます。合わせて覚えておきましょう。

放物線の場合分け問題は、応用しようと思えばいくらでもできます。

例えば定義域ではなく放物線が動く場合とか、定義域の幅を広げたり縮めたりするとか。

ですがこの定義域が動くパターンをマスターしておけば、場合分けの基礎はしっかり固まります。

楓

定義域の位置で最大値最小値が異なる感覚は掴めたかな？

二次関数で学ぶ場合分け｜二次関数の場合分けのコツ

楓

それでは先ほどのパターンの解法ポイントを見ていこう！

先ほどご紹介したパターンの場合分け問題は、定義域が動くという特徴があります。

放物線の場合、

で、圧倒的に考えやすくなります。

定義域が動く場合の場合分け

では、定義域の条件ですが任意の実数\(a\)を用いて\(a≦x≦a+1\)と表せます。

小春

任意の実数\(a\)ってどういう意味？

どんな実数の値を取っても大丈夫、という意味だよ。

楓

小春

じゃあ、\(a=-8\)でも\(a=3.4\)でも大丈夫ってこと？

なんでもいいよ。どんな実数\(a\)でもOKとすることで、定義域が固定されず動くという条件を表現できるんだ。

楓

定義域\(a≦x≦a+1\)では\(x=a\)が左端の\(x\)座標、\(x=a+1\)が右端の\(x\)座標を表しています。

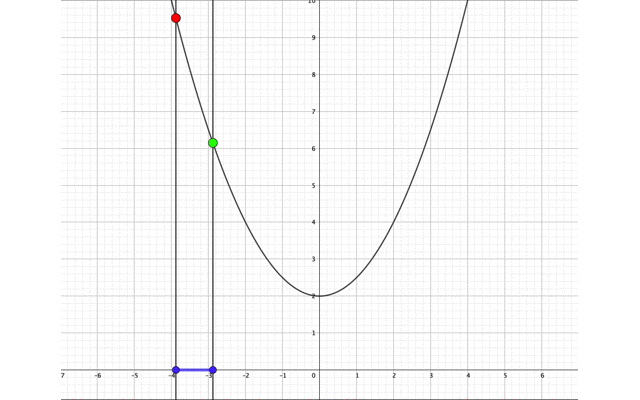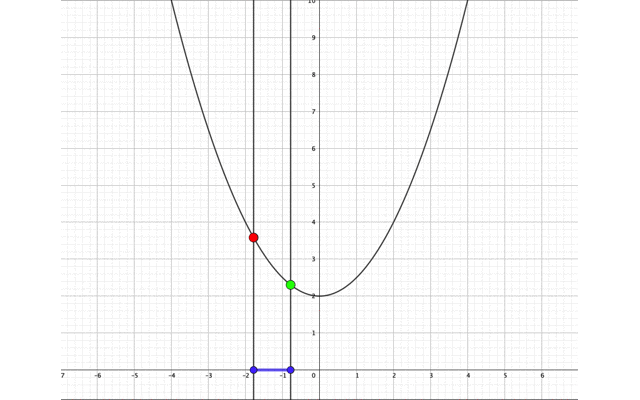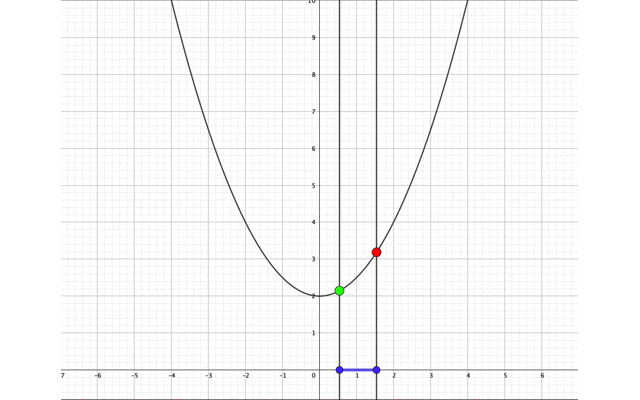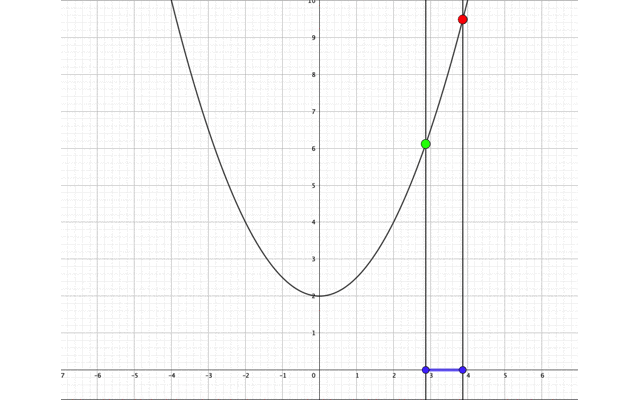
すなわち下の図の場合は、\(x=a\)のとき最大値、\(x=a+1\)のとき最小値になるということです。

step
1まずは最大値から考える。

ではまず最大値に着目して考えていきましょう。

楓

繰り返すけど放物線の場合分けでは、頂点を着眼点にするといいよ。

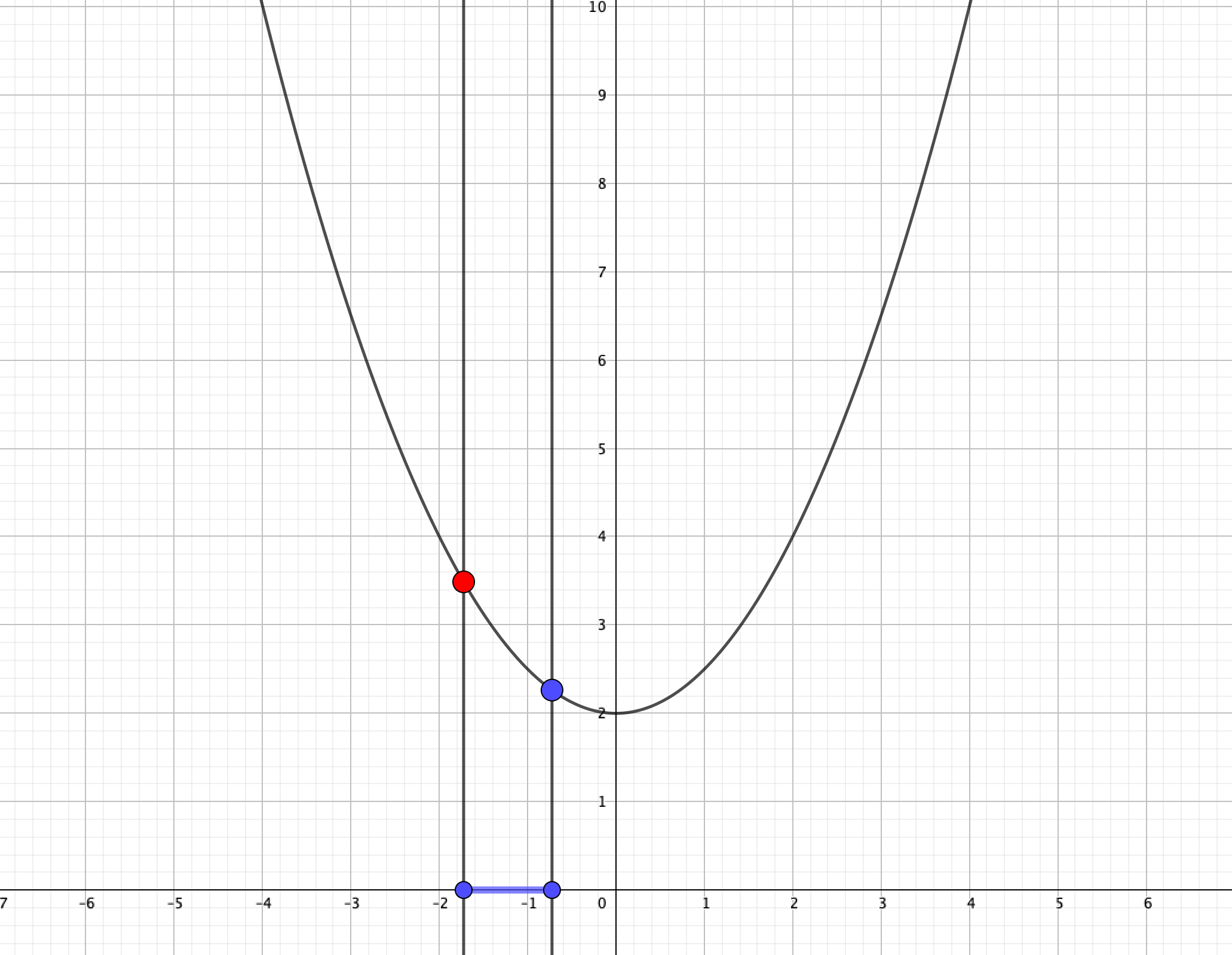
\(x=a,x=a+1\)がどちらも負のとき、最大値は当然\(x=a\)のときですね。

しばらくは\(x=a\)のとき最大値を取るのですが、頂点を越えだしたあたりから\(x=a+1\)のときの\(y\)座標が上昇を始めます。

\(x=a\)のとき最大値
 
 

\(x=a+1\)のときの\(y\)座標が上昇を始める。
 

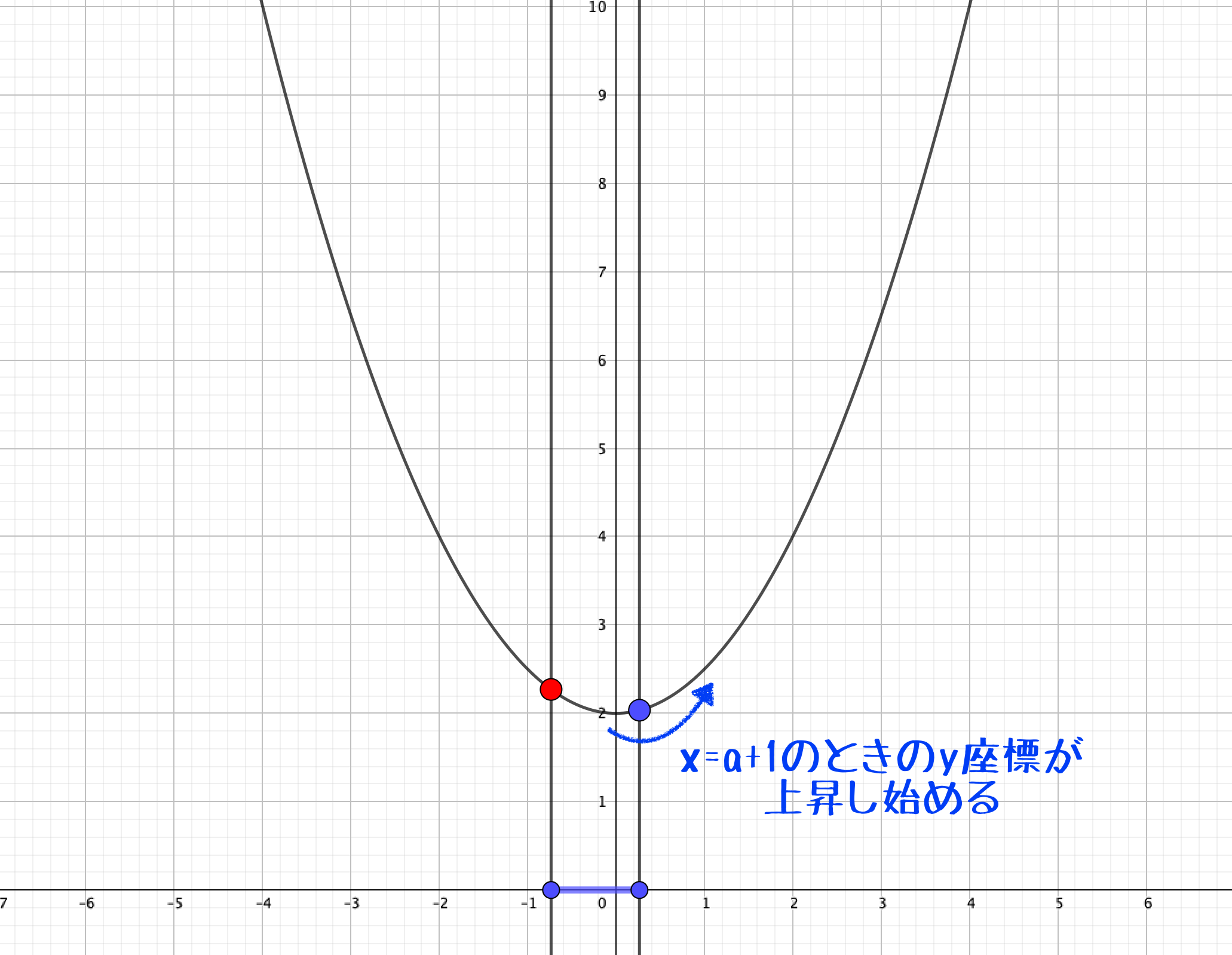
そして、\(x=a,x=a+1\)の真ん中に頂点が存在するとき、両者の\(y\)座標は等しく、そして最大値となります。

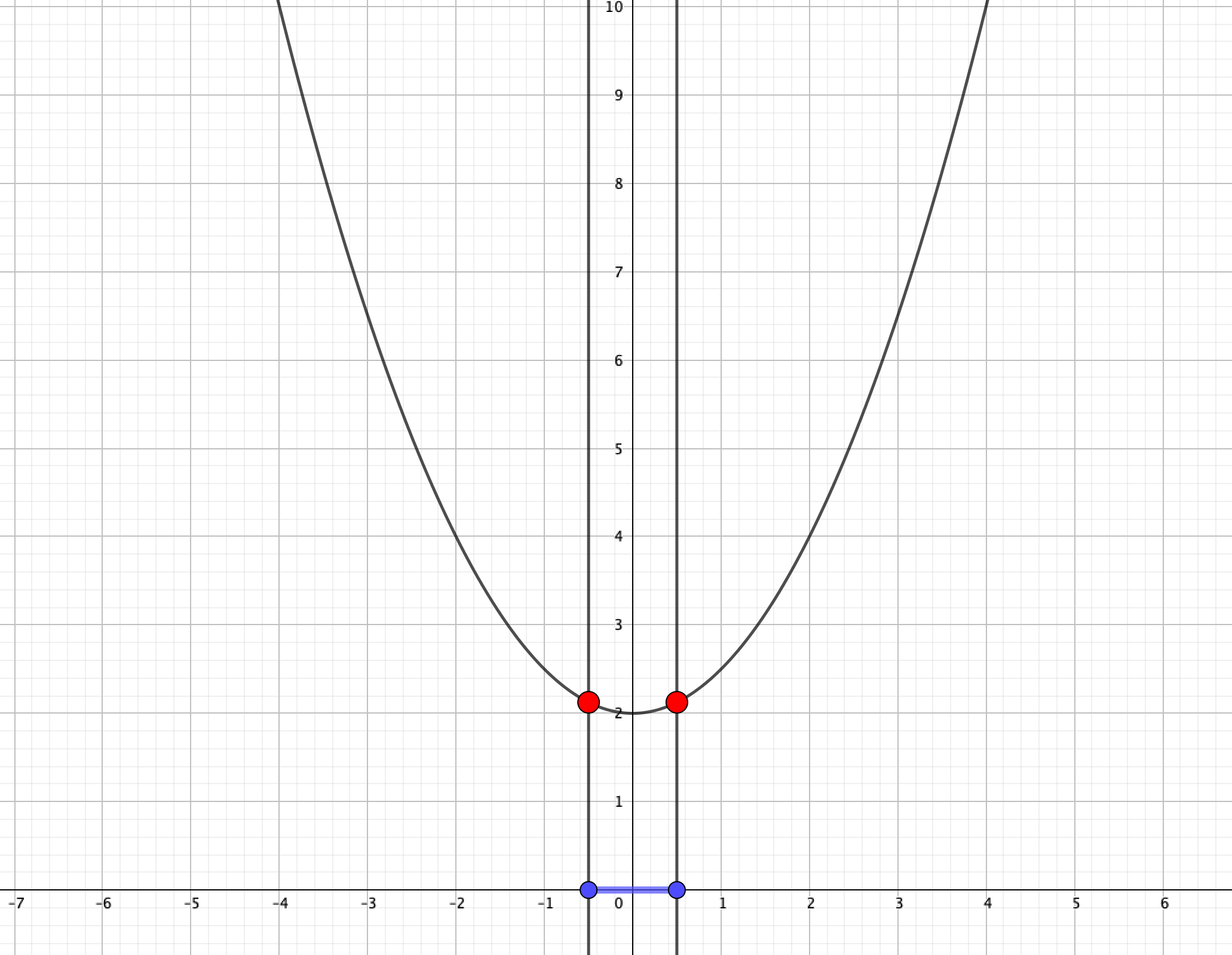
\(x=a,x=a+1\)の真ん中に頂点が存在するということは、

$$\frac{a+(a+1)}{2}=0（原点のx座標）$$

を計算して、\(a=-\frac{1}{2}\)のときに両者の高さが等しくなることわかります。

小春

つまり両点の高さが等しくなるまでの\(a<-\frac{1}{2}\)では、\(x=a\)のとき最大ということね！

そう、ここで最大値の条件が切り替わったので1つ目の場合分けのタイミングだよ。

楓

そしてさらに\(a\)の値が大きくなると\(x=a,x=a+1\)の\(y\)座標の上下関係が逆転し、\(x=a+1\)のとき最大値となります。

\(x=a,a+1\)のとき最大値

\(x=a+1\)のとき最大値

小春

つまり、高さが等しくなって以降の\(\frac{1}{2}<a\)のときは、\(x=a+1\)のときが最大ということだね

そしてまた条件が変わったので、2つ目の場合分けのタイミングってこと。

楓

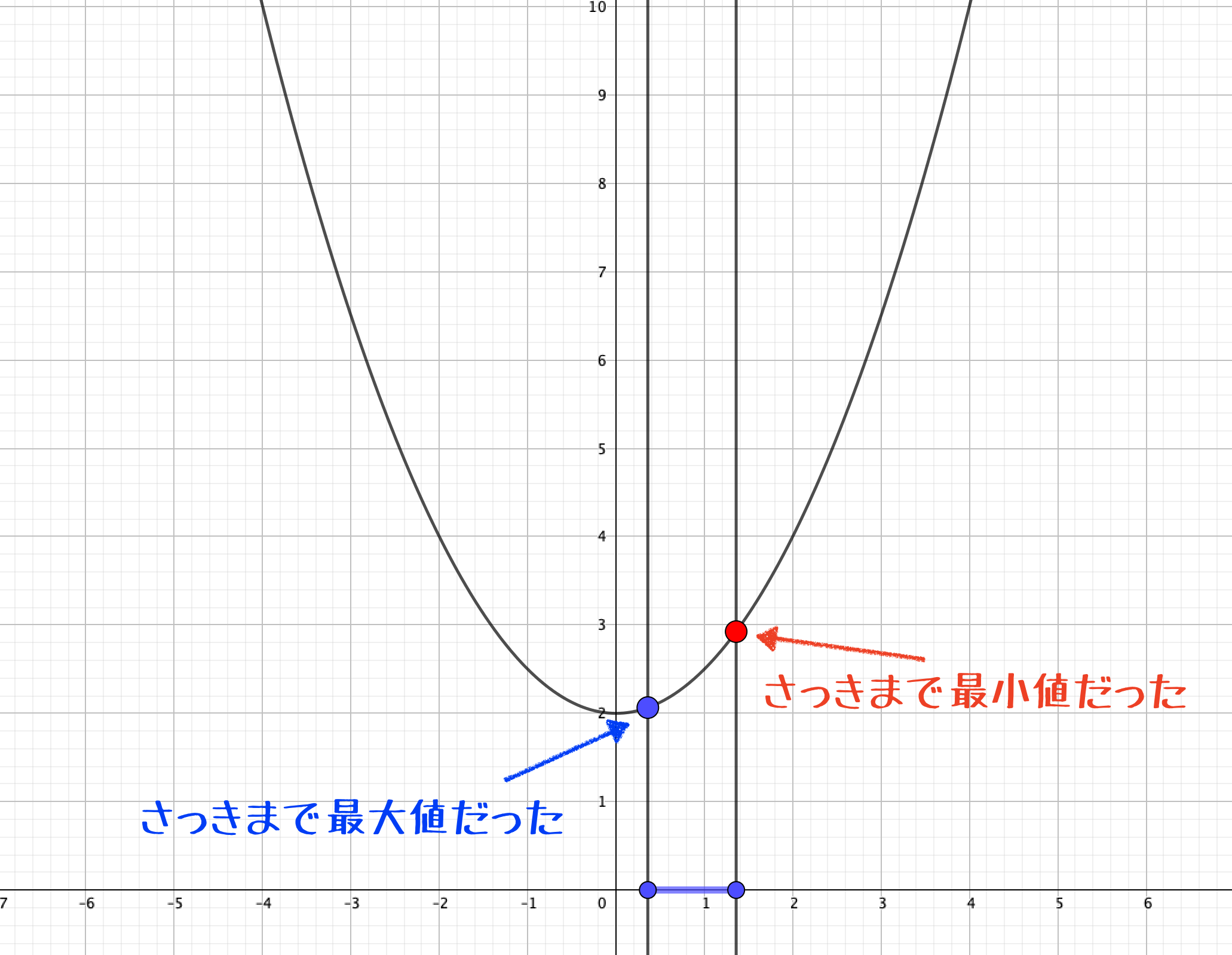
以上のことから、最大値に関しては

の３パターンがあることがわかりました。

楓

要は軸が区間より右にあるか、軸が区間内にあるか、軸が区間より左にあるかで考えればいいよ。

step
2次に最小値を考える。

次に最小値を考えましょう。

楓

最大値最小値を一気に考えると分かりにくいから、バラバラに求めて後で合体させるよ。

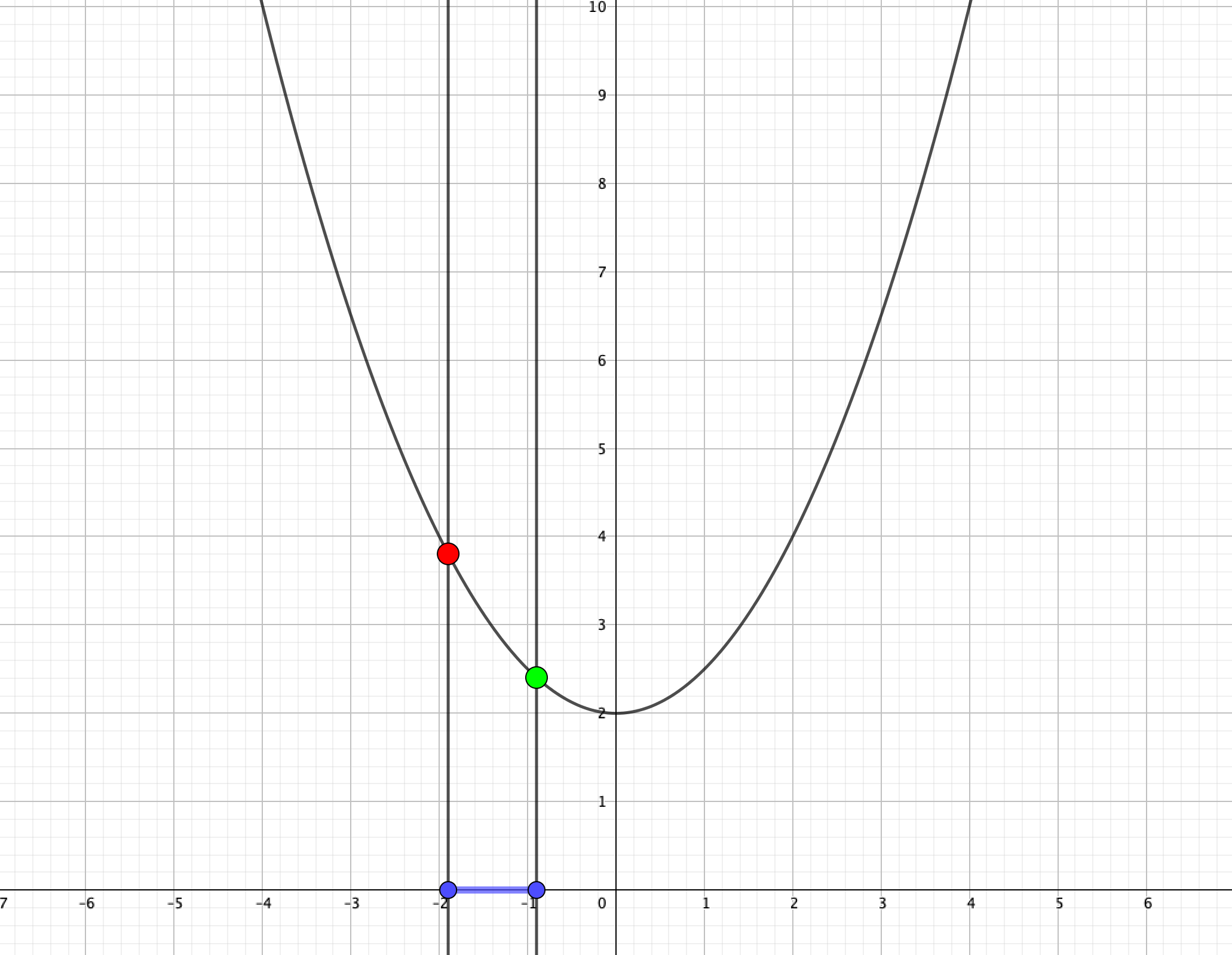
先ほどと同じ順番で考えると、\(x=a,x=a+1\)がどちらも負のとき、最小値は\(x=a+1\)のときです。

ですが\(x=a+1\)のときの点が、頂点を超えると次第に上昇するため、グラフの最小値は頂点に切り替わります。

\(x=a+1\)が頂点を超えるまでは、ずっと最小値を取る。
 

\(x=a+1\)が頂点を超えると、最小値は頂点になる。 
 

小春

つまり\(a+1<0\)か\(0≦a+1\)で場合分けができるってことね！

移項すると、\(a<-1\)か\(-1≦a\)のときで場合分けできるってことになるね。

楓

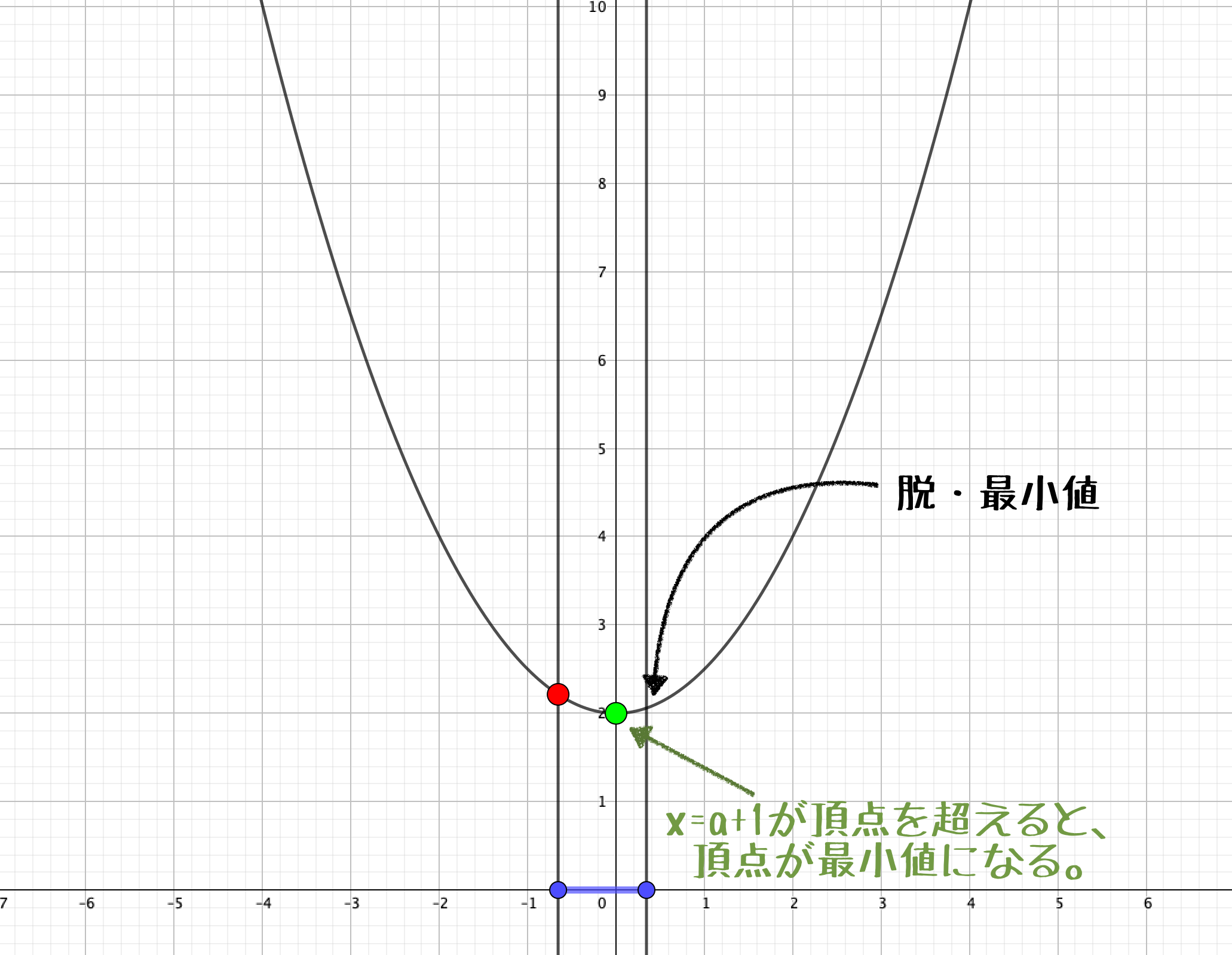
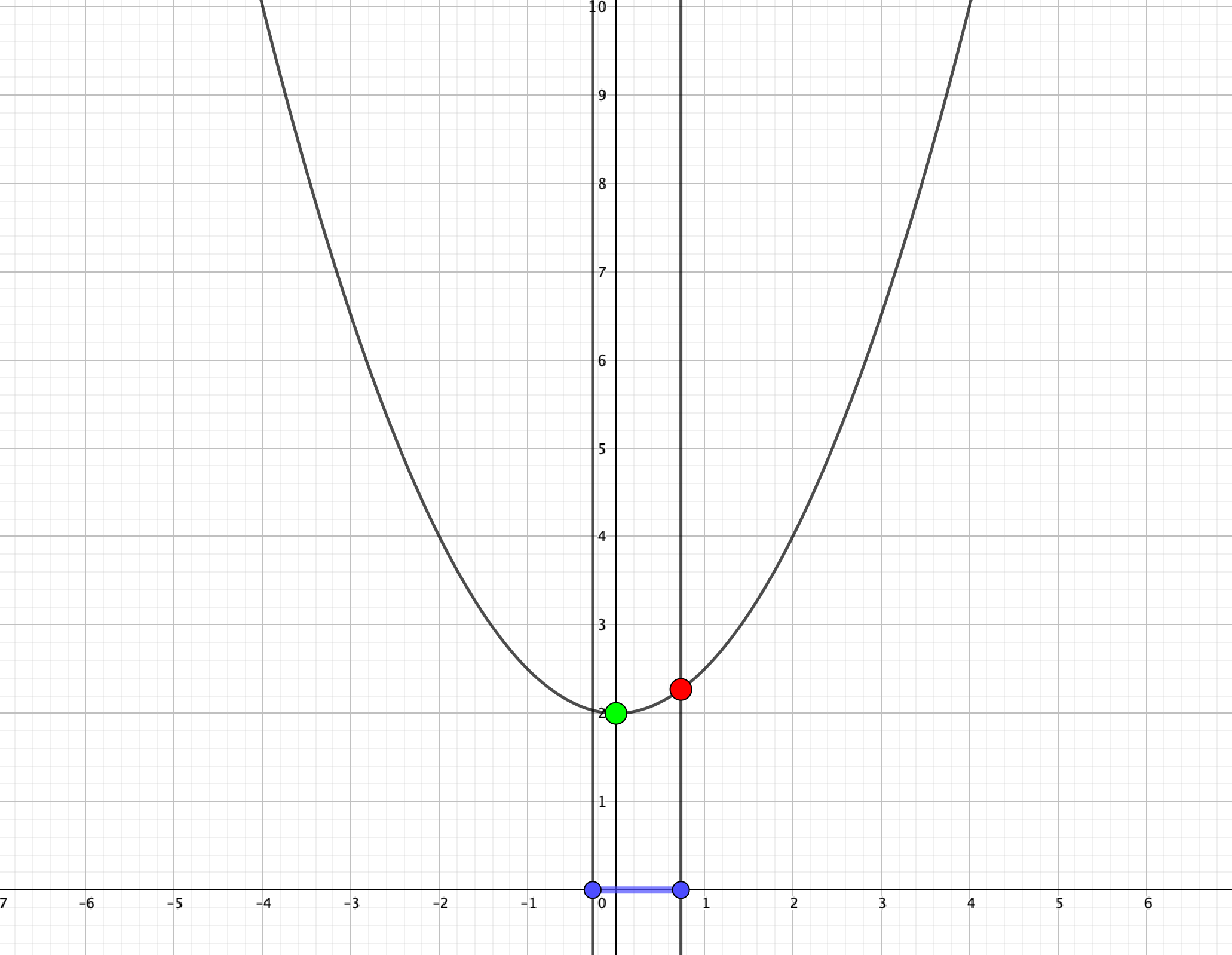
そして、\(x=a\)が頂点を通過するまでは最小値はずっと頂点となります。

しかし、\(x=a\)が頂点を通過すると最小値は\(x=a\)のときに切り替わります。

\(x=a\)が頂点を超えるまでは、頂点がずっと最小値を取る。
 

\(x=a\)が頂点を超えると、最小値は\(x=a\)のときになる。 
 

楓

値が切り替わったから、場合分け！

つまり、\(a≦0\)のときと\(0<a\)のときで場合分けができるね。

小春

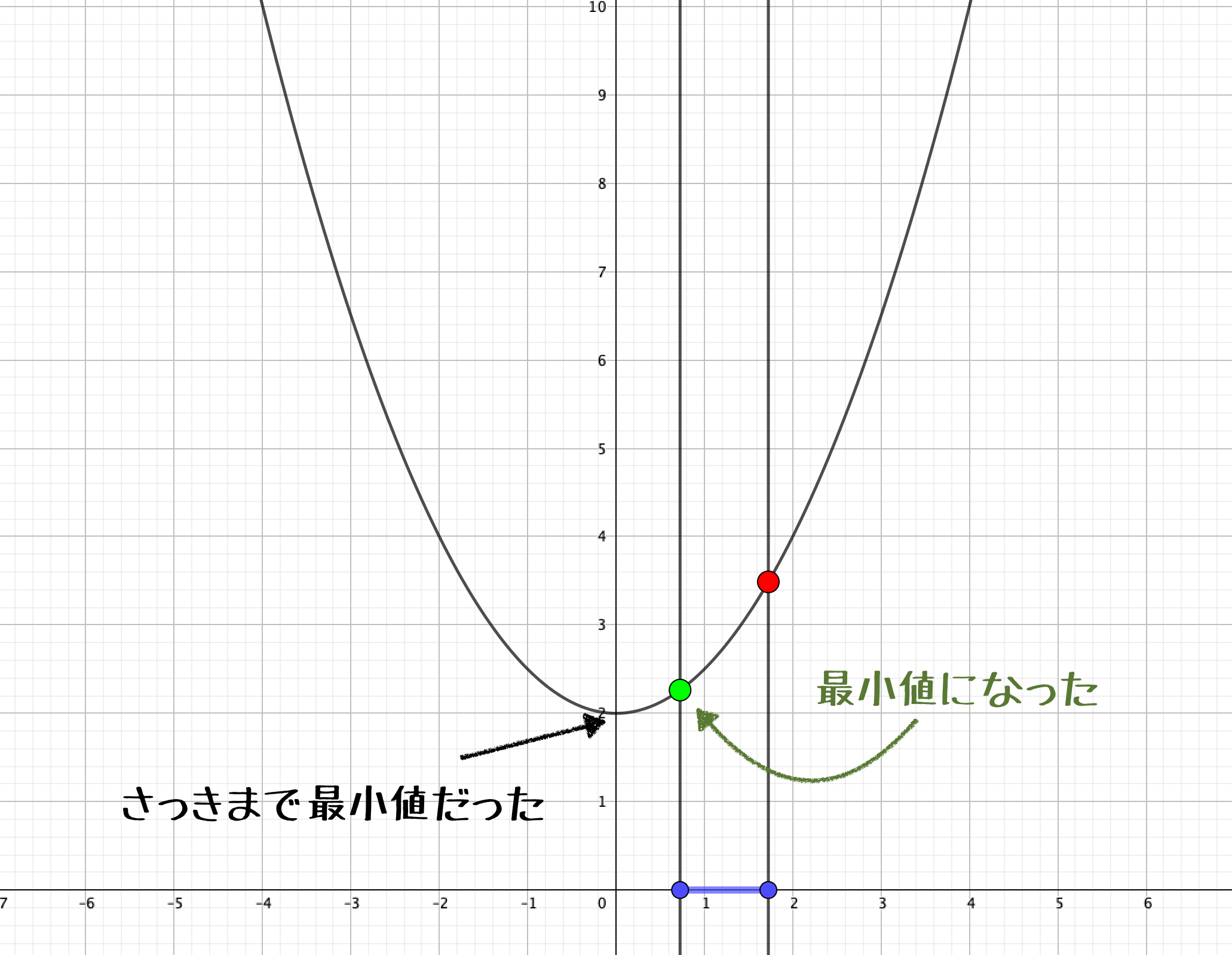
このように

• 定義域内に頂点が含まれていない場合、頂点に近い方が最小値になる。
• 定義域内に頂点が含まれている場合、頂点が最小値になる。

ということがわかります。また最小値に関しては

の３パターンがあることがわかりました。

step
3最大値、最小値を同時に考える。

さて、最後に最大値と最小値の条件を合体させて考えていきます。

\(a\)の定義域に着目して、

①\(a<-1\)のとき、\(x=a\)で最大値\(a^2+2\)、\(x=a+1\)で最小値\(\left(a+1\right)^2+2\)をとる。

②\(-1≦a<-\frac{1}{2}\)のとき、\(x=a\)で最大値\(a^2+2\)、\(x=0\)（頂点）で最小値2をとる。

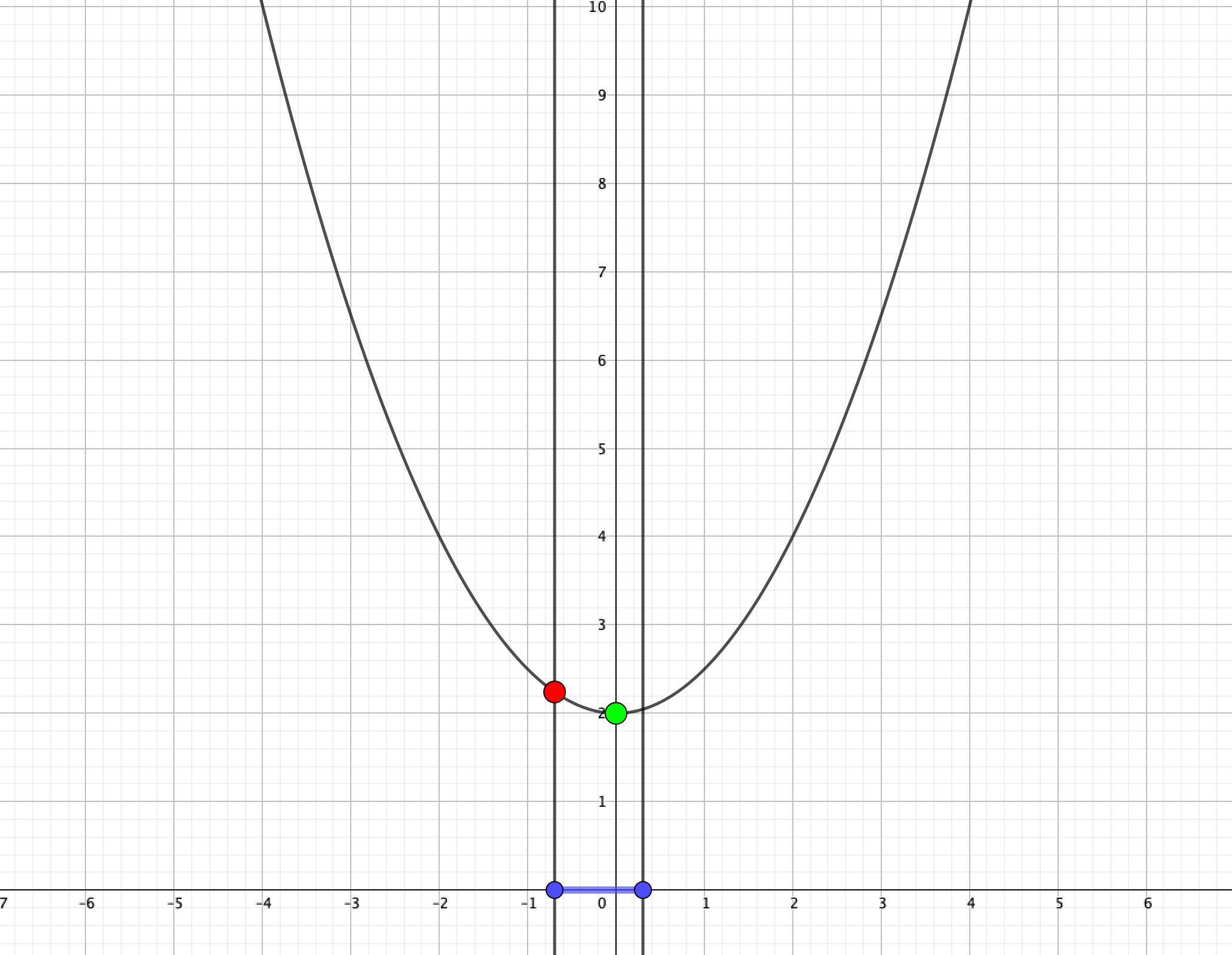
③\(a=-\frac{1}{2}\)のとき、\(x=a,a+1\)で最大値\(\frac{9}{4}\)、\(x=0\)（頂点）で最小値2をとる。

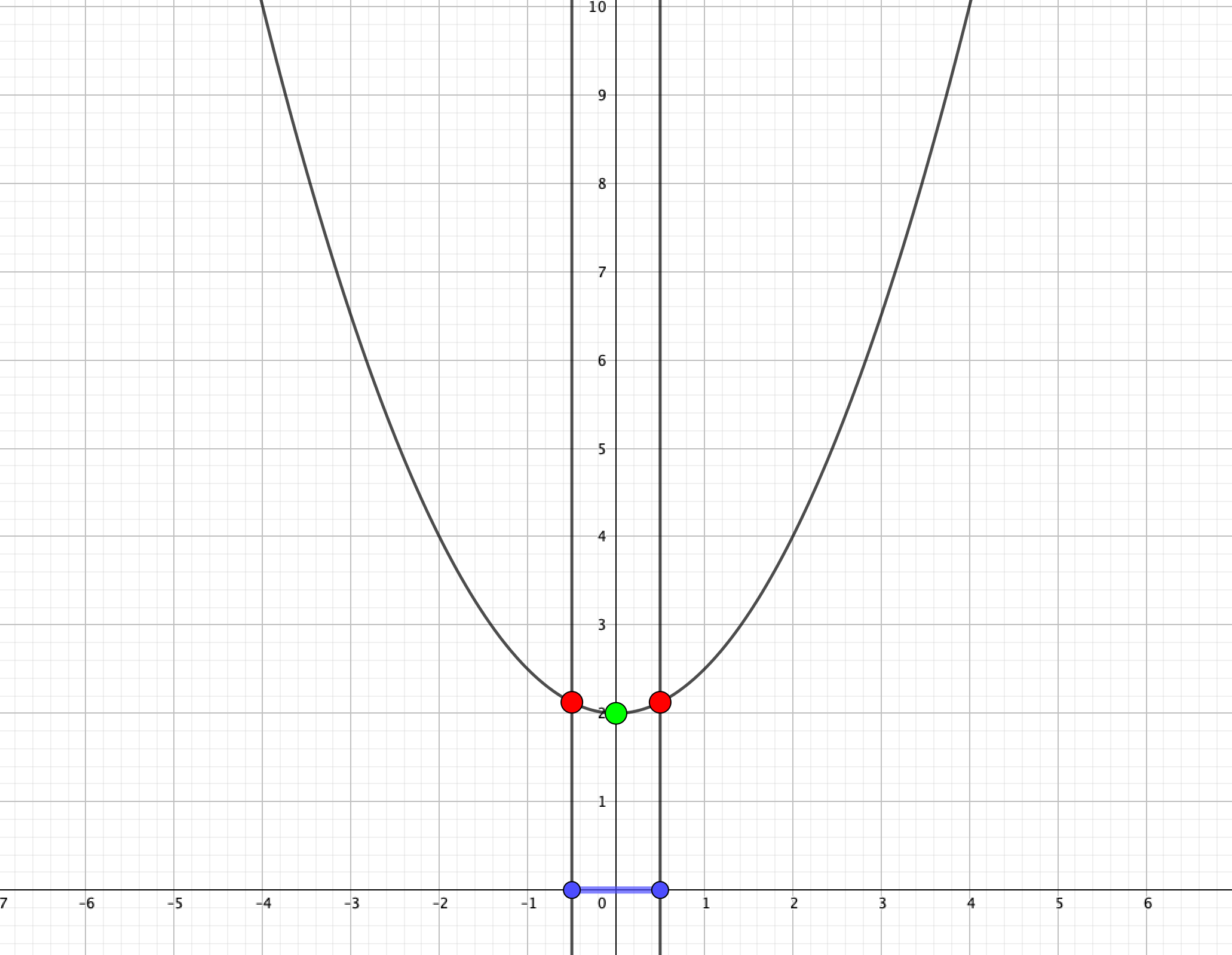
④\(-\frac{1}{2}<a≦0\)のとき、\(x=a+1\)で最大値\(\left(a+1\right)^2+2\)、\(x=0\)（頂点）で最小値2をとる。

⑤\(0<a\)のとき、\(x=a+1\)で最大値\(\left(a+1\right)^2+2\)、\(x=a\)で最小値\(a^2+2\)をとる。

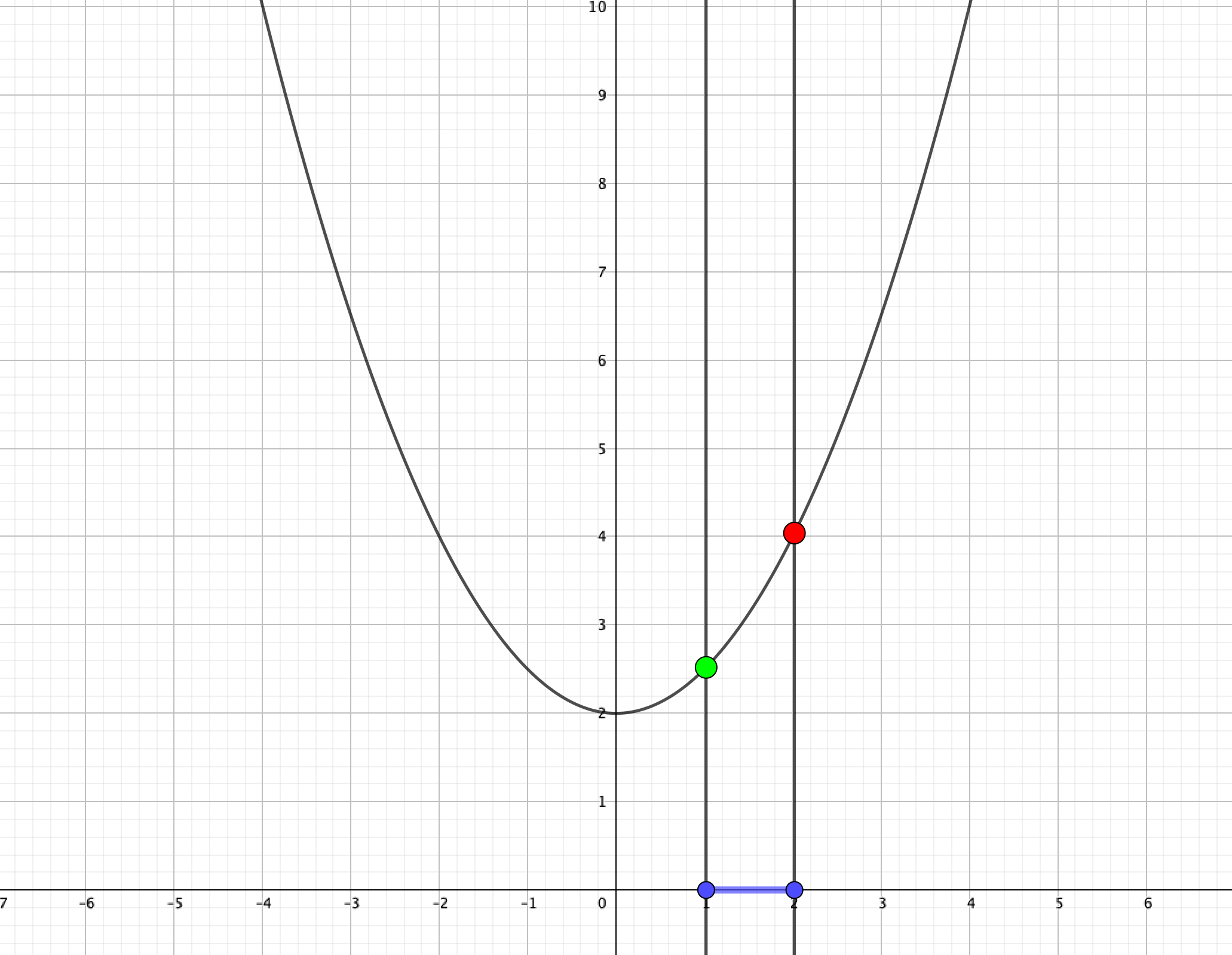
となります。

楓

頂点が定義域の真ん中にあるときは、最大値が2つあるから結構特殊。

二次関数で学ぶ場合分け｜場合分けをしたくなるポイントと場合分けのコツ

このように、二次関数の場合分けは最大値と最小値で分けて考えることで考えやすくなりました。

これも一種の場合分けと見なせます（最大値となる場合と、最小値になる場合）。

繰り返しになりますが、場合分けはどんな条件でも答えが1つなら必要ありません。

特定の条件で答えが変化するとき、場合分けしていきましょう。

例題でも何度か登場した、「最大値（最小値）が切り替わる」という表現は、この考え方に当てはまります。

特定の条件で値が切り替わるようであれば、それが場合分けのタイミングなので逃さないようにしましょう。

二次関数で学ぶ場合分け｜まとめ

最後に重要なポイントを書いておこう！

今回は二次関数を例題に扱いましたが、場合分けは数学の様々な場面で頻繁に登場します。そして二次関数はその中でも場合分けのいい例題を作りやす題材です。

そのため二次関数には今回取り扱ったもの以外にも、様々な場合分けが存在します。

しかしどんな問題でも、「値が特定の条件で切り替わる」ときに場合分けをするという感覚を大切にしてください。

以上、「場合分けの極意」でした。