Today's Topic
二次関数\(y=ax^2+bx+c\)を
$$y-q=a(x-p)^2$$
の形にすることを平方完成という。





こんなあなたへ
「平方完成の意味がわからない。何したいの?」
「変形のコツが知りたい!」
この記事を読むと、この意味がわかる!
- $$y=x^2+2x-6$$のグラフを描け。
- $$y=x^2$$を横に-3、縦に+2平行移動させたグラフの方程式を求めよ。

Contents
二次関数のベース:\(y=ax^2\)について知ろう

あなたは中学校の頃に、\(y=ax^2\)のグラフについて勉強したことを覚えているでしょうか?
ここの理解が抜けていると、二次関数はすごくイメージしにくくなるのでまずはここをしっかり押さえていきましょう。

関数\(y=ax^2\)(\(a\)は比例定数)のグラフを見てみると、次のような性質があることがわかります。
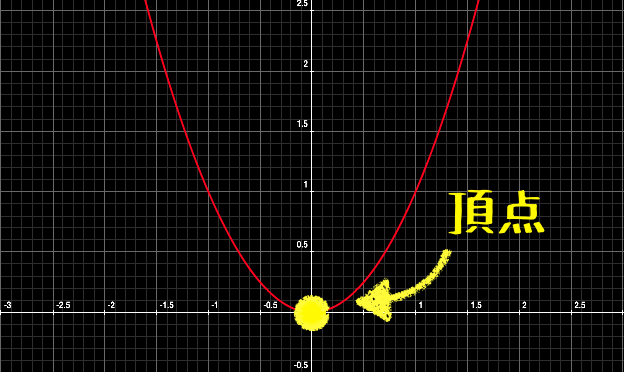
- 放物線を描き、その頂点は原点と一致する。
- \(x\)軸で線対称。

では比例定数\(a\)の値を変化させていくと、グラフはどのように変化するのでしょうか。
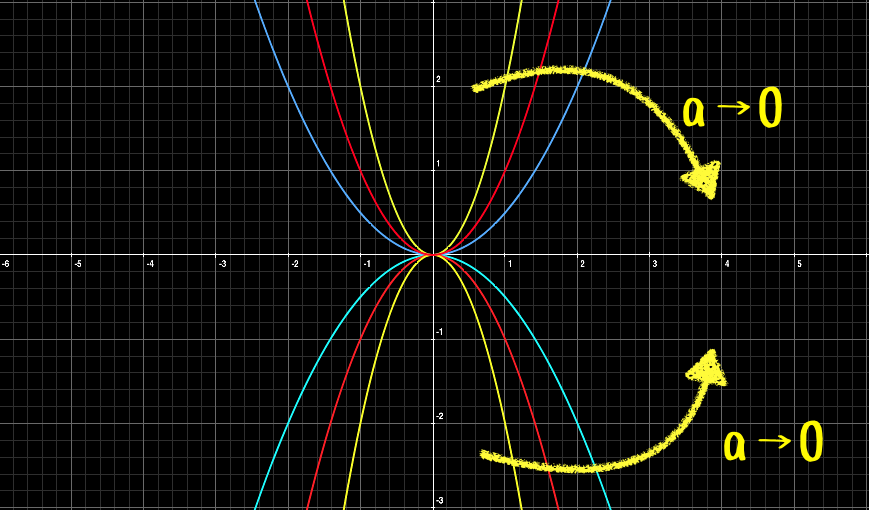
下のグラフでは
- \(y=2x^2\)
- \(y=x^2\)
- \(y=\frac{1}{2}x^2\)
の時を調べてみました。



これは\(a\)の値が負の場合も同様で、とにかく\(a\)の値が0に近づくほどグラフが広がることを覚えてください!


復習はここまで。
中学校のときまではここでおしまいだったのですが、この放物線にはある制限があります。
それは頂点が常に原点で固定されているということ。
頂点が固定されていない放物線の方程式を考えよう。
たとえば、ベース\(y=ax^2\)の頂点をつまんで、図のように移動させたとき、移動したグラフの方程式はどう表せるのでしょうか。
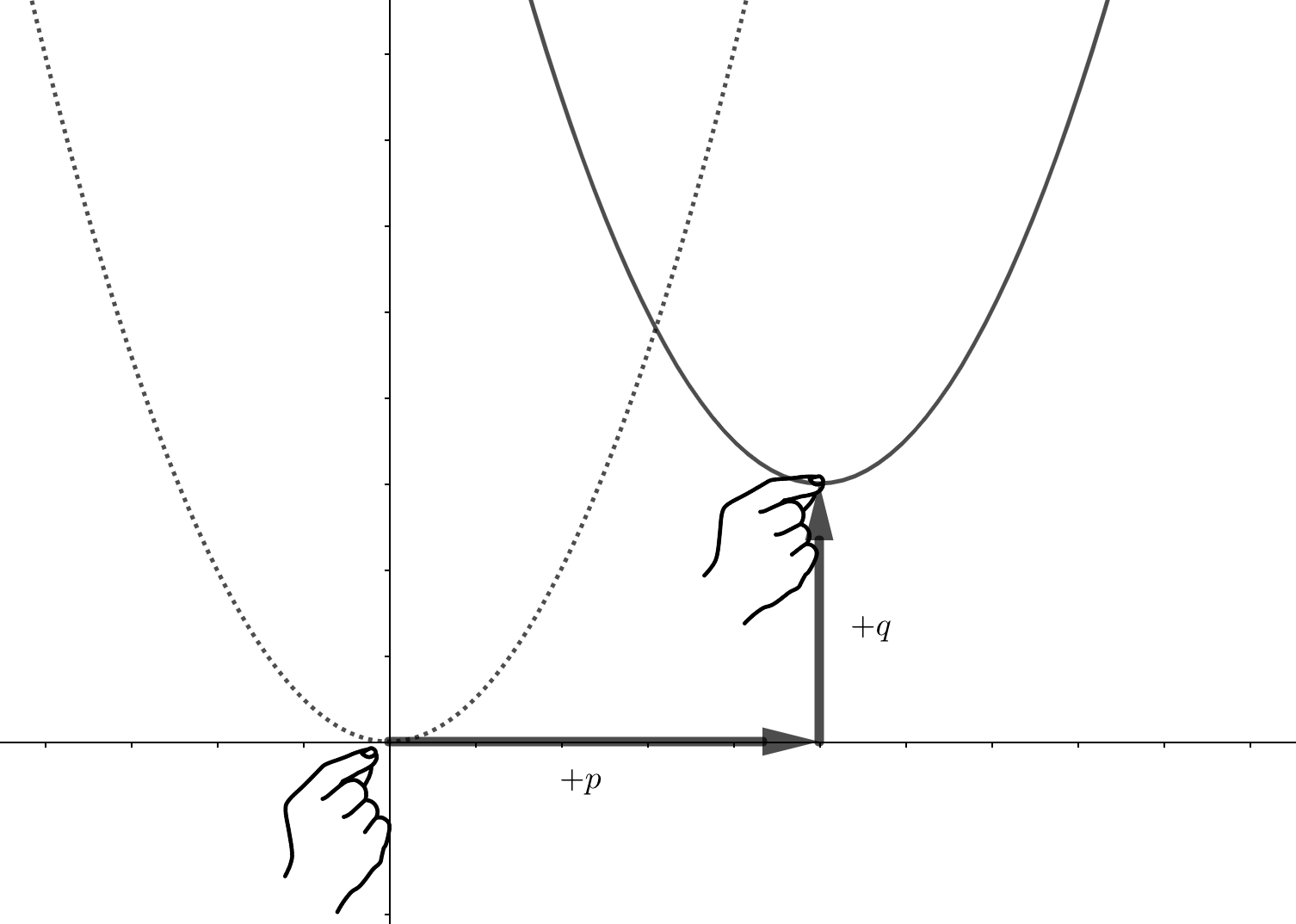
このような動きのことを平行移動といい、次のような公式がありました。
平行移動の公式
関数\(y=f(x)\)のグラフを、\(x\)軸方向に\(+p\)、\(y\)軸方向に\(+q\)だけ平行移動したグラフは、
$$y-q=f(x-p)$$
と表せる。

平行移動について復習したい人はこちらを参考にしてください。
続きを見る

平行移動のやり方と公式の意味→符号を入れ替えて書き換えるだけで、グラフの問題がスラスラ解ける
今回の場合、\(y=ax^2\)のグラフを\(x\)軸方向に\(+p\)、\(y\)軸方向に\(+q\)だけ平行移動したグラフなので、移動したグラフの方程式は
と表すことができそうです。
平行移動した放物線の式から押さえておきたい2つのポイント


【ベース】
$$y=ax^2$$
【横に\(p\)、縦に\(q\)平行移動】
$$y-q=a\left(x-p\right)^2$$
ベースの式と、平行移動した後の式を見比べた時、
- どちらも\(a\)の値→開き具合は変わらない
- ベースの\(x,y\)が、平行移動すると\((x-p),(y-q)\)に書き換わってる
という2つの点に注目してください。


また、頂点もグラフの動きと同じように平行移動しているわけですから\(x\)軸方向に\(+p\)、\(y\)軸方向に\(+q\)だけ移動させた先の頂点O'の座標は\(O'(p,q)\)となります。
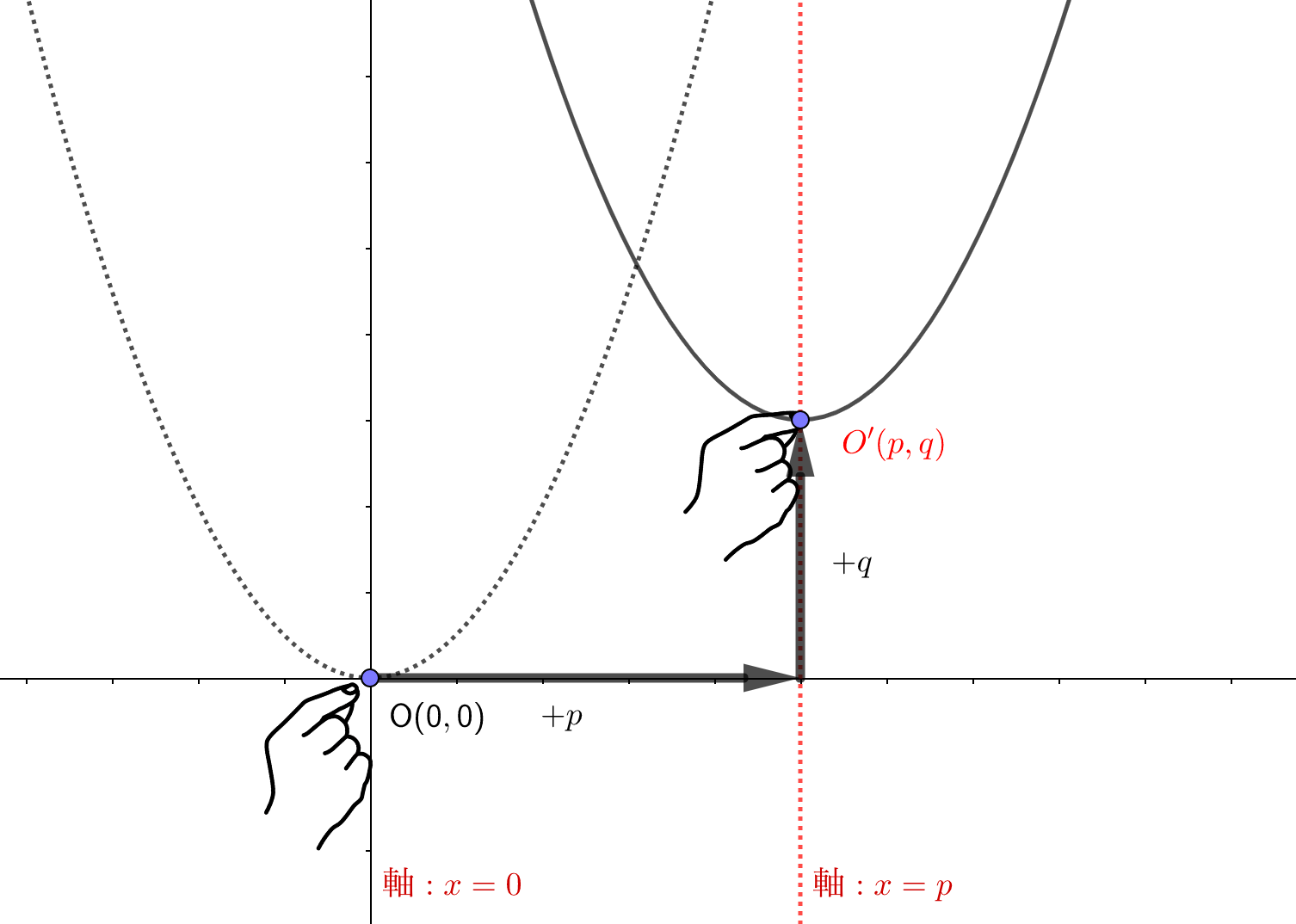



平方完成の意味


ここまでで分かったことを、もう一度、カンタンにまとめると、
重要ポイント
\(y=ax^2\)のグラフを\(x\)軸方向に\(+p\)、\(y\)軸方向に\(+q\)だけ平行移動したグラフの方程式は
$$y-q=a\left(x-p\right)^2$$
と表せる。


これを利用すると、次のような問題が解けます。
例題
\(y+3=\left(x-3\right)^2\)のグラフを描け。
(解答)
開き具合の同じベース\(y=x^2\)と見比べると、
$$y\rightarrow y+3$$
$$x\rightarrow x-3$$
のように書き換わっているので、\(y=x^2\)を\(x\)軸方向に+3、\(y\)軸方向に-3だけ平行移動した放物線を描けば良い。
よって、下図の赤い放物線のようになる。
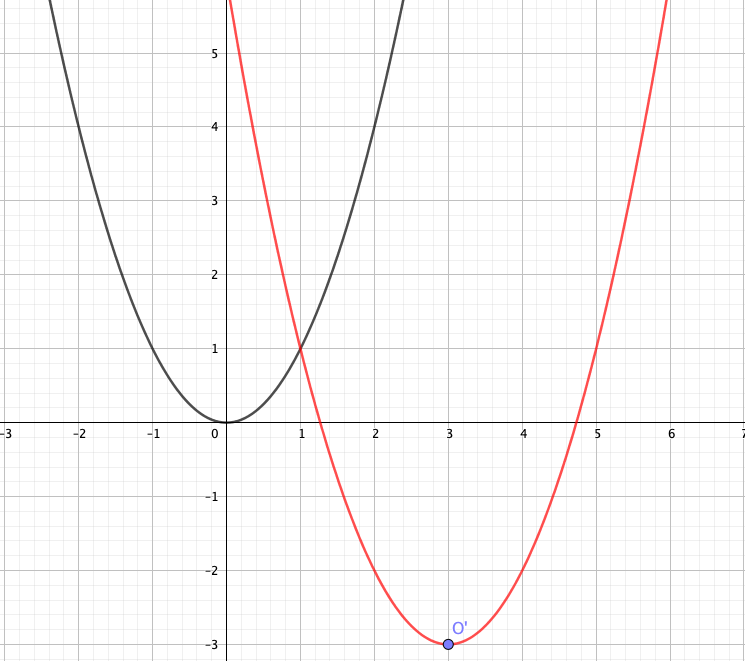

つまりあなたはすでに、\(y-q=a\left(x-p\right)^2\)の形で表された放物線であれば、どんなものでもグラフに表すことができるようになっているのです。




では次の二次方程式のグラフはどのようになるのでしょうか。
例題
\(y=2x^2+6x-4\)のグラフを描け。
このグラフを書くためにはどうすればいいでしょうか。
答えは単純で、グラフが描ける\(y-q=a\left(x-p\right)^2\)の形に直してあげればいいのです。
このようにグラフが描けるように、二次関数を\(y-q=a\left(x-p\right)^2\)の形に変形させることを平方完成といいます。
ポイント
平方完成は一般的な二次方程式を\(y-q=a\left(x-p\right)^2\)の形にすることで、どのような放物線を描くのか調べるために行う。
平方完成の仕方は後述しますが、\(y=2x^2+6x-4\)は
のように平方完成することができます。
\(y=2x^2+6x-4\)がどんなグラフを描くかすぐにはわかりませんが、
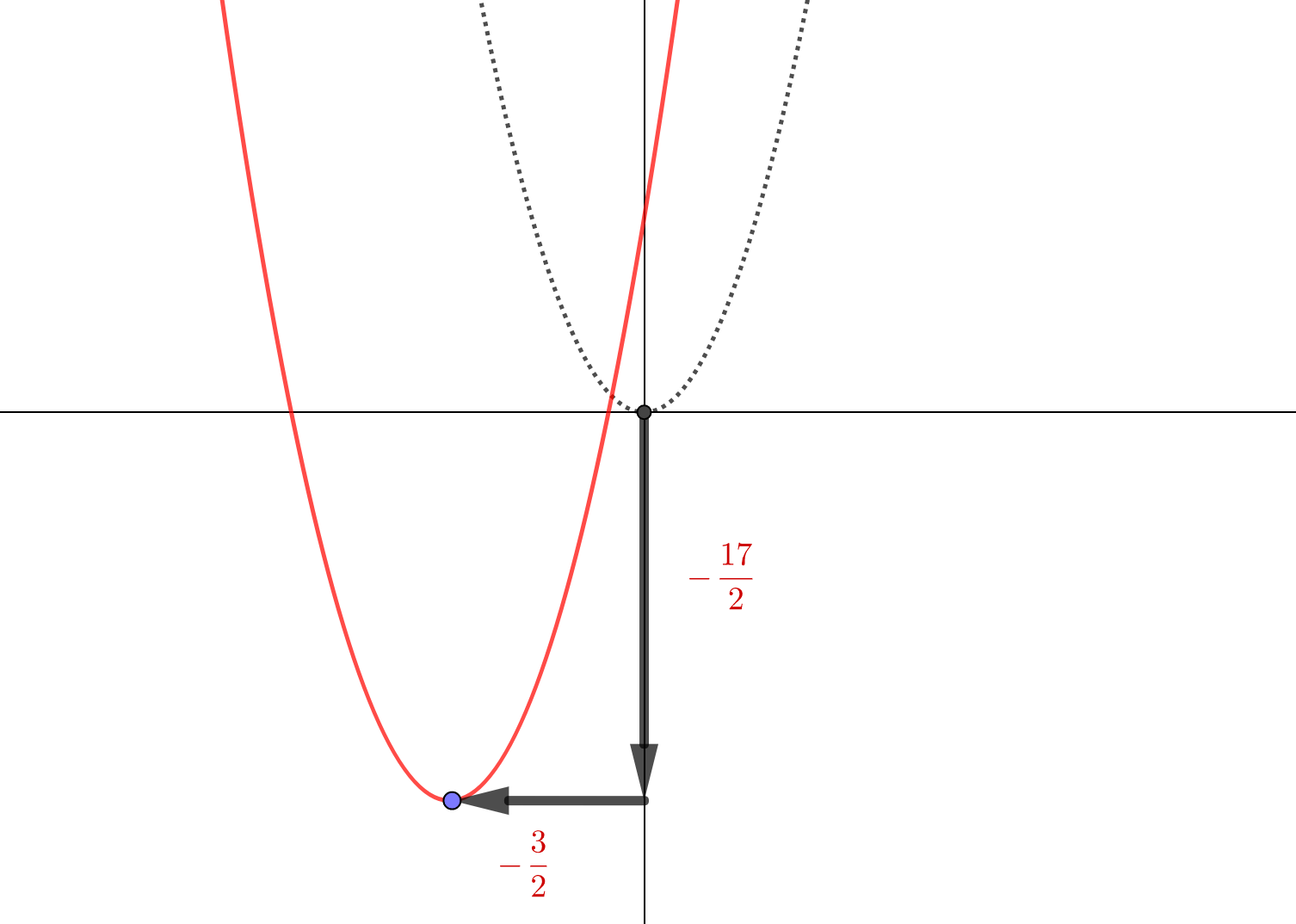
\(y+\frac{17}{2}=2\left(x+\frac{3}{2}\right)^2\)であれば、\(y=2x^2\)のグラフを
- 横に\(-\frac{3}{2}\)
- 縦に\(-\frac{17}{2}\)
だけ平行移動したグラフだとすぐにわかります。

平方完成 変形のコツ
それでは平方完成のやり方のポイントを、先ほどの例題
$$y=2x^2+6x-4$$
を実際二平方完成しながら解説していきます。
平方完成をカンタンに行うためには、3つのステップを順に踏んで行きます。
-
STEP1\(x^2\)の係数で、\(x\)がついている項までくくる。平方完成しても開き具合が一定であることに着目します。
-
STEP2カッコの中の式が出現するような、2乗の展開公式を考える。\((x-□)^2\)を展開して、\(x^2+○ x\)が出現する公式を探します。
-
STEP3余分な定数項を調整する。\(x\)がついていない定数項をスッキリ整理します。
順に詳しく解説していきます。
step
1\(x^2\)の係数で、\(x\)がついている項をくくろう。
まず\(y=2x^2+6x-4\)の\(x^2\)の係数2に着目します。
この2で方程式の\(x\)がついている項をくくった、
$$y=2\left(x^2+3x\right)-4$$
の形を作ります。




step
2カッコの中の式を含むような展開公式を思い出そう。
次に、変形した式のカッコの中身、\(y=2\left(\color{red}{x^2+3x}\right)-4\)の赤の部分に着目します。
展開すると
が登場するような2乗の展開公式\((x-□)^2\)を探してみましょう。
すると、
が思いつきます。


\(\left(x+\frac{3}{2}\right)^2=\color{red}{x^2+3x}+\frac{9}{4}\)の\(\frac{9}{4}\)を移項すると、
となります。
では、この\(\color{red}{x^2+3x}\)に着目して、STEP1の式を変形してみると
step
3定数項を整理しよう。
最後に、くくっていた\(x^2\)の係数を展開しましょう。
すると
となります。
定数項の部分を計算すると、
そして定数項を移項することで、
となるので、無事\(y-q=a\left(x-p\right)^2\)の形にすることができました。




平方完成のまとめ→平行移動したベースを意識しよう!


まとめ
- 二次関数の\(x^2\)の係数\(a\)は、放物線の開き具合を表し、\(a\)の値が0に近づくほど放物線は開く。
- 二次関数\(y-q=a\left(x-p\right)^2\)はベース\(y=ax^2\)が\(x\)軸方向に\(+p\)、\(y\)軸方向に\(+q\)だけ平行移動したときの式である。
- \(y=ax^2+bx+c\)のグラフを描くためには、平方完成を施し\(y-q=a\left(x-p\right)^2\)の形にすれば良い。
今回は平方完成の意味について、記事を書きました。
最後にもう一度、大事なポイントをおさらいしますが、
重要ポイント
\(y=ax^2\)のグラフを\(x\)軸方向に\(+p\)、\(y\)軸方向に\(+q\)だけ平行移動したグラフの方程式は
$$y-q=a\left(x-p\right)^2$$
と表せる。
これが本当に平方完成の全てを意味しています。
「グラフを描くために、平方完成をする』。この気持ちを大切にしてください。
以上、「二次関数 平方完成の意味と変形のコツ」でした。
Q. $$y=x^2+2x-6$$のグラフを描け。
$$\ $$
この2次方程式のグラフを描くためには、平方完成をすれば良い。
方程式の\(x^2+2x\)に着目すると、
$$(x+1)^2=x^2+2x+1$$
より、\(x^2+2x=(x+1)^2-1\)。
$$\ $$
よって、与えられた式は
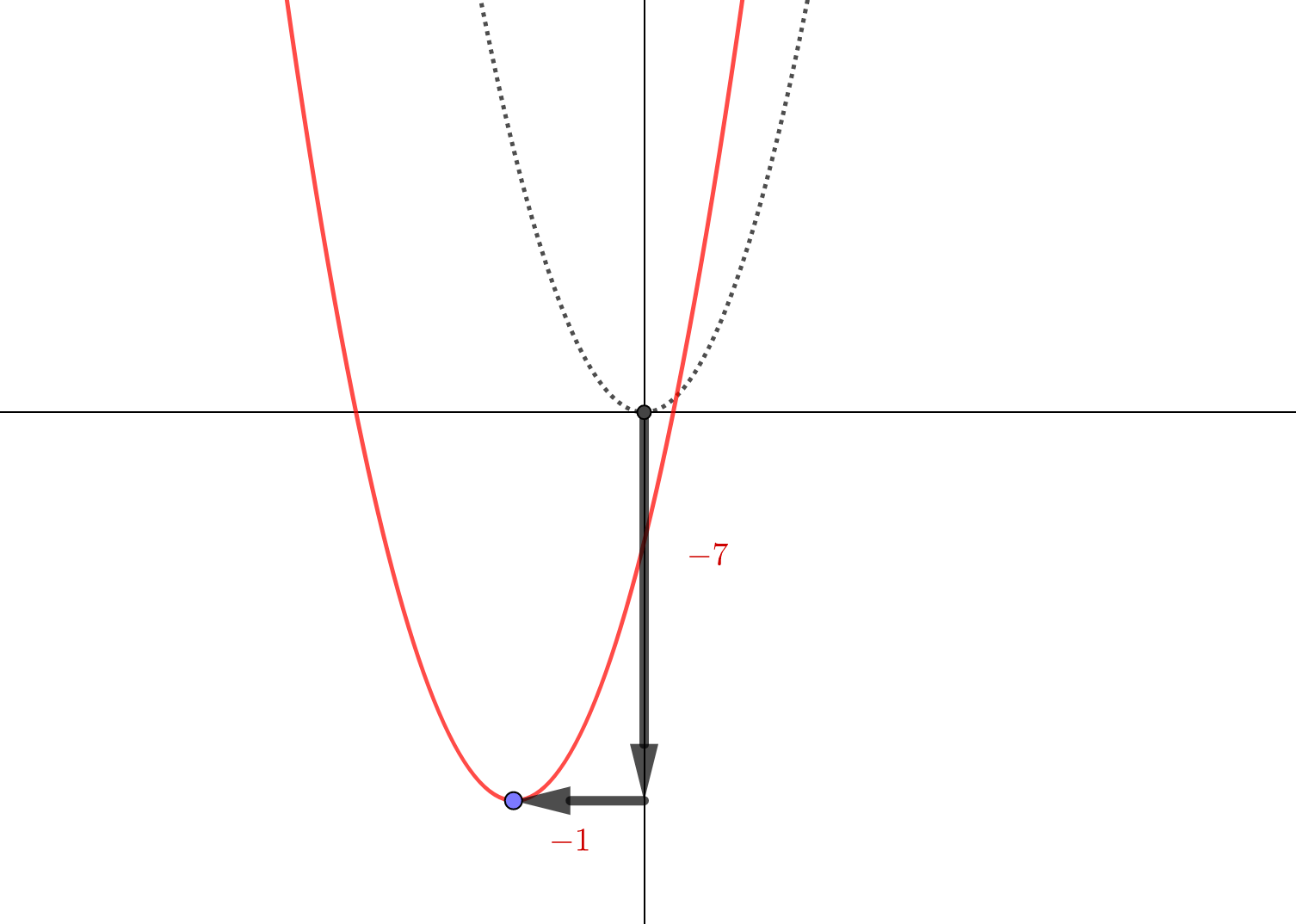
$$y+7=(x+1)^2$$
となる。これは\(y=x^2\)を横に\(-1\)、縦に\(-7\)平行移動したグラフである。

Q.$$y=x^2$$を横に-3、縦に+2平行移動させたグラフの方程式を求めよ。
$$\ $$
$$x\rightarrow x+3$$
$$y\rightarrow y-2$$
のように書き換えれば良い。
よって、
$$y-2=(x+3)^2$$








