Today's Topic
平方完成や一般形など、二次関数の様々な形と意味



こんなあなたへ
「問題を見て何をしていいかわからない」
「変形の仕方も変形する意味もわからない・・・。」
この記事を読むと、この意味がわかる!
- 点\((2,-3)\)を頂点とし、点\((4,-7)\)を通るような放物線の方程式を求めよ。
- 二次関数\(y=\frac{1}{2}x^2-x+1\)の最大値、最小値があれば求めよ。

二次関数の変形①:平方完成
平方完成の形にした二次関数からは、次のようなことがわかります。
- グラフが描ける!
- 軸の方程式がわかる!
- 頂点の座標がわかる!

例
$$y=x^2-5x+6 = \left(x-\frac{5}{2}\right)^2+\frac{9}{4}$$
平方完成の方法については、こちらで詳しくまとめています。
-

-
【平方完成】中学数学から解説!公式の意味と変形の仕方→無理やり二乗を作ると、グラフの動きがわかる!
続きを見る
平方完成は、基本的には平行移動の仕方を知るための変形。
頂点が原点の放物線を基準に、どのようにズレたのかがわかります。
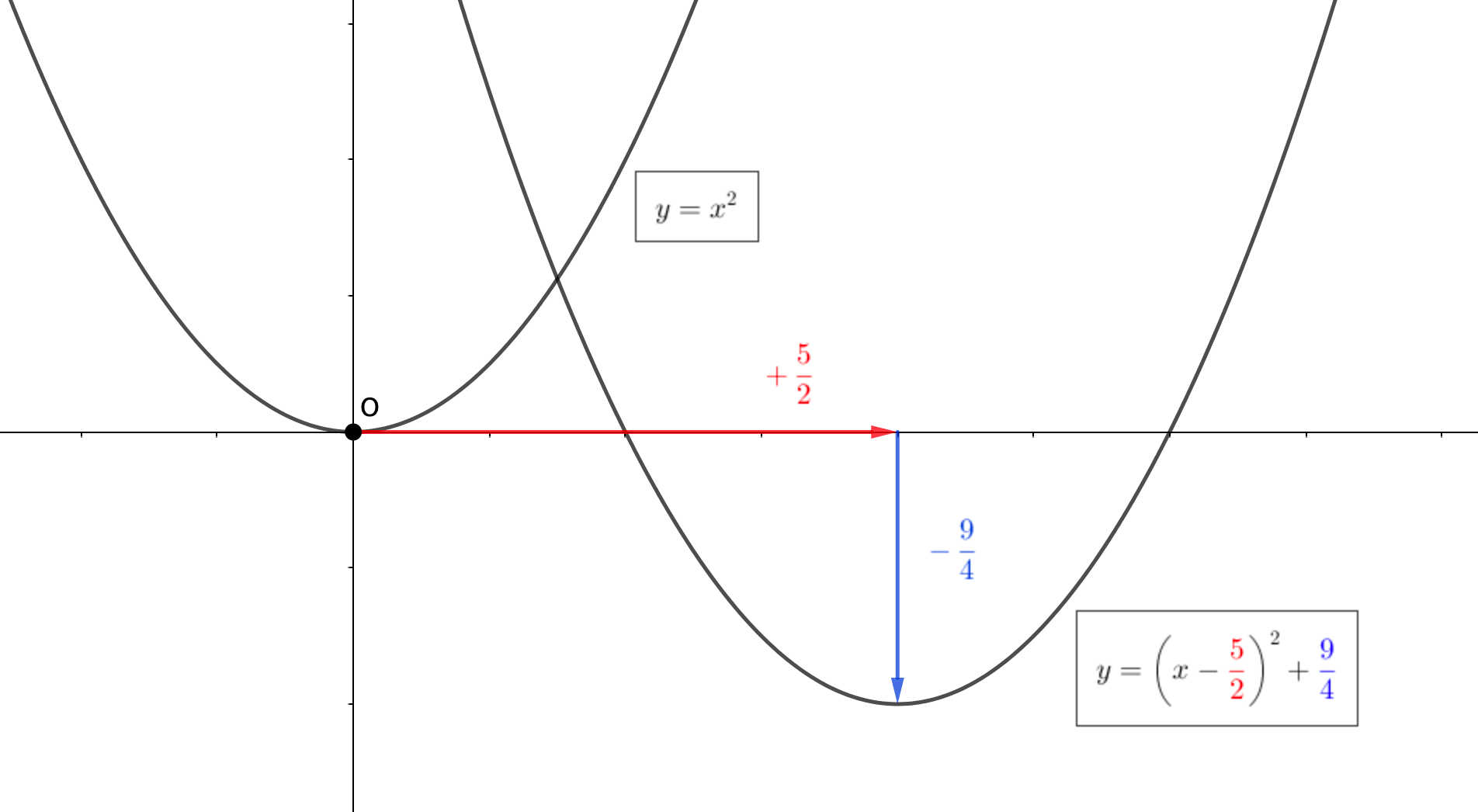

ただよく観察してみると、
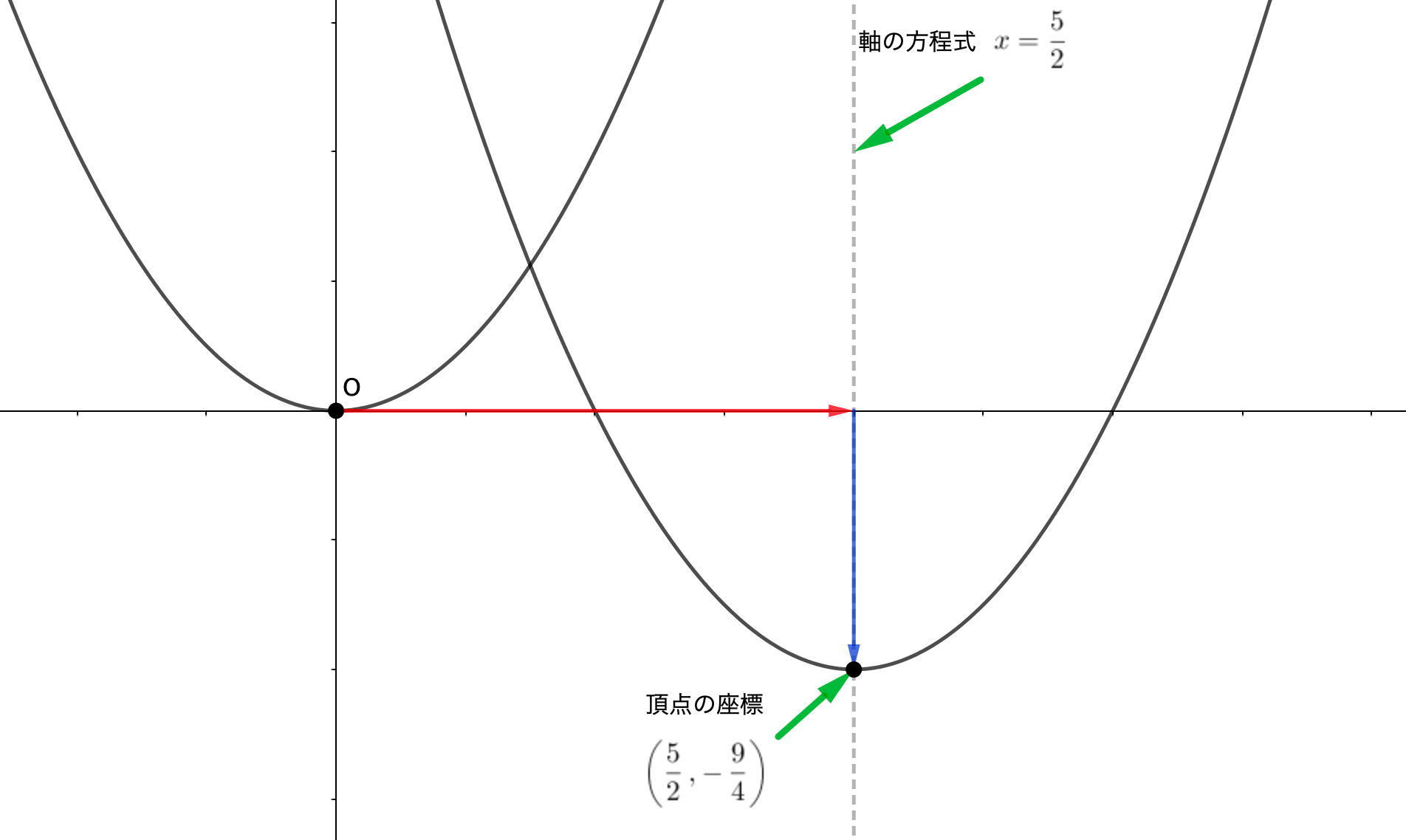
- 頂点の座標は、原点から平行移動している
- 軸は\(x\)軸と垂直に交わり、頂点を通る直線のこと
なので、おまけのような形で頂点の座標と、軸の方程式を得られます。

二次関数の変形②:因数分解
因数分解の形にした二次関数からは、次のようなことがわかります。
- \(x\)軸と交わるかどうか
- \(x\)軸との交点座標


例
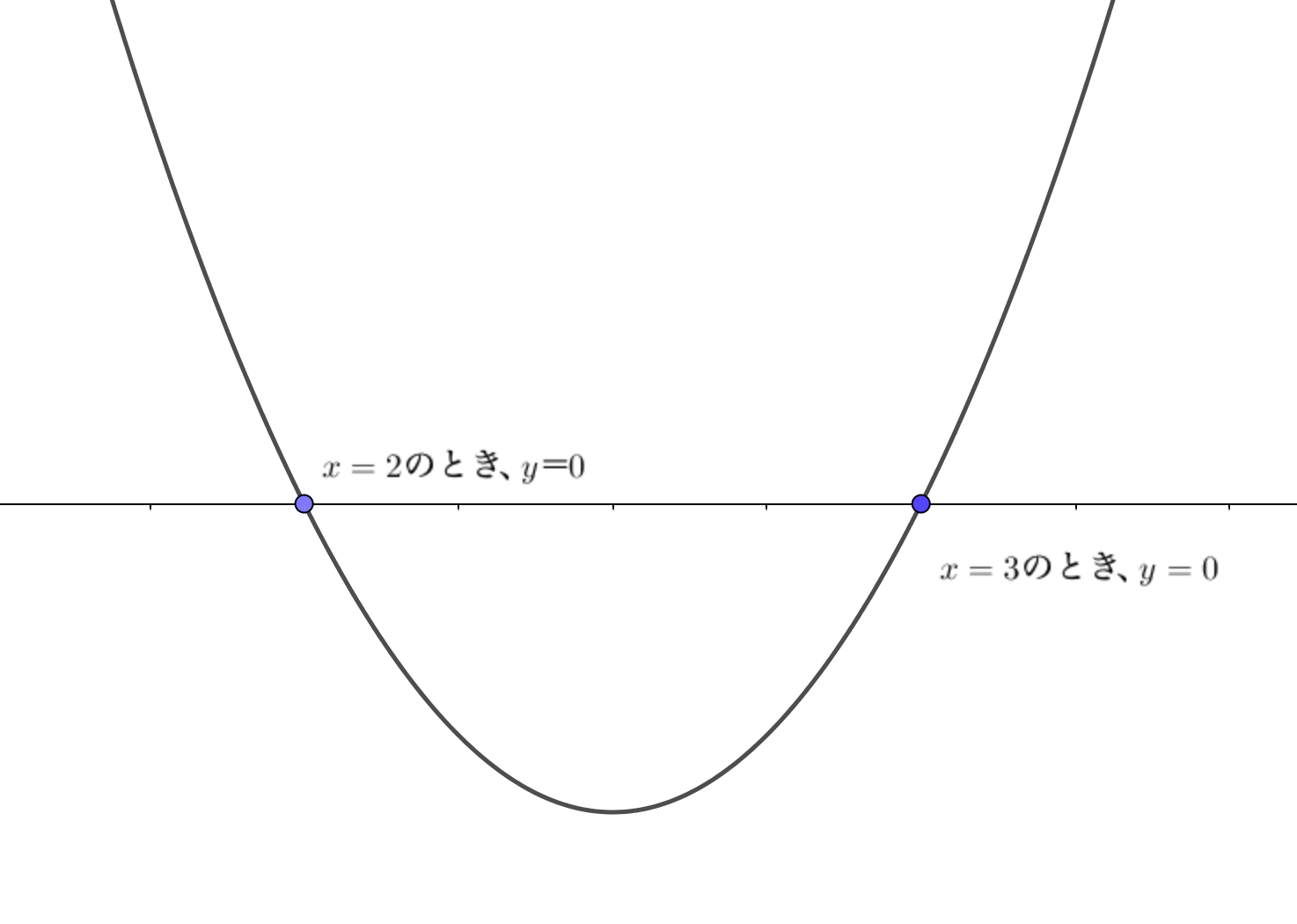
$$y=x^2-5x+6 = (x-2)(x-3)$$
因数分解形にすることで、\(y=0\)となるような\(x\)の値が瞬時に求められるようになります。

二次関数の変形③:一般形
一般形とは展開された形のこと。
例
$$y=x^2-5x+6$$
この形を使うのは、基本的に
- 放物線とほかのグラフの交点を求める
- 3つの点が与えられ、それらを通る放物線の方程式を求める
ときだけです。
実際に問題を見てみましょう。
例題
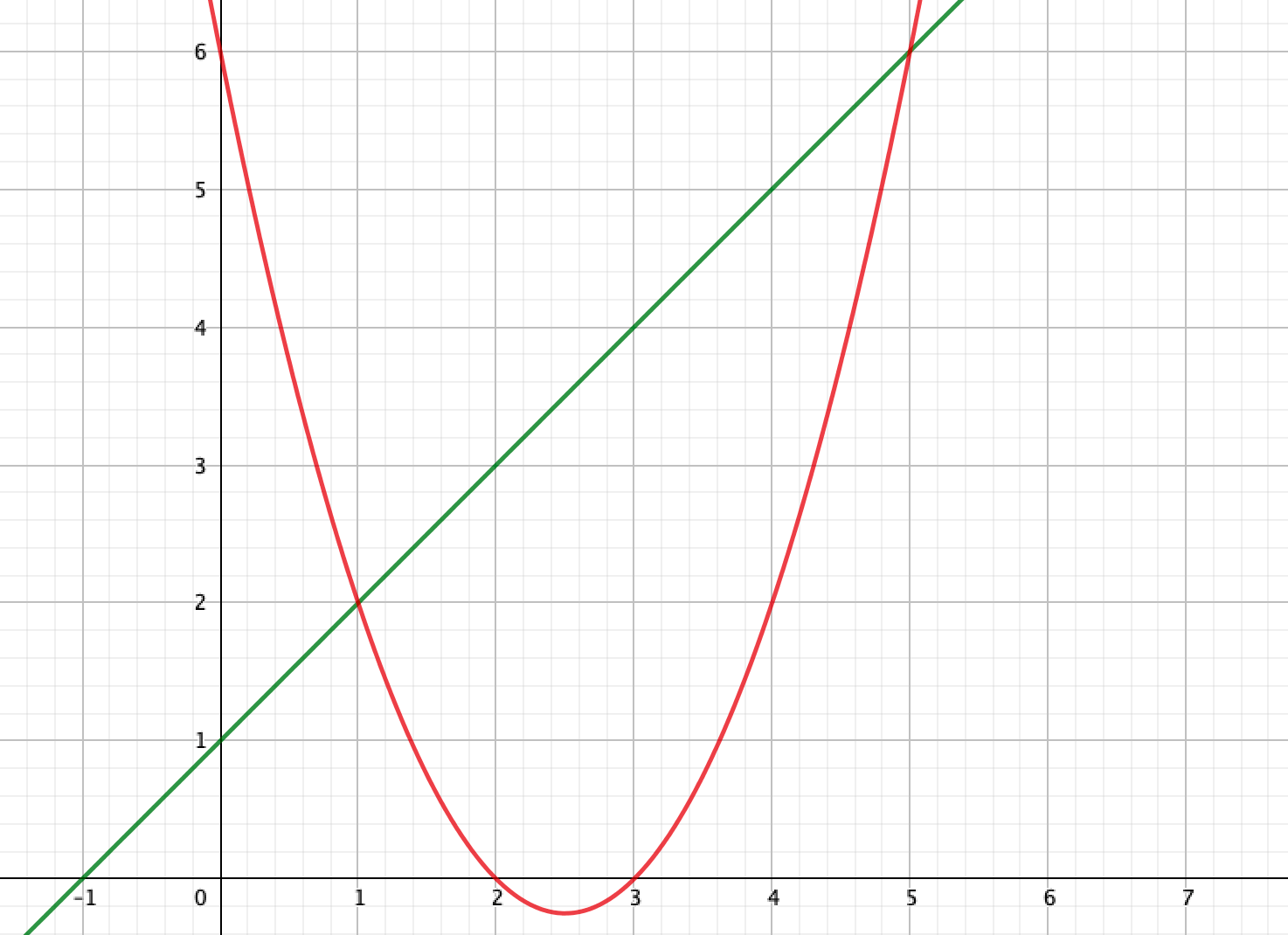
放物線\(y= \left(x-\frac{5}{2}\right)^2+\frac{9}{4}\)と直線\(y=x+1\)の交点座標を求めよ。
$$ \left(x-\frac{5}{2}\right)^2+\frac{9}{4} = x+1$$
を解けば良い。
左辺を展開して、
$$x^2-5x+6 = x+1$$
整理すると、
$$x^2-6x+5=(x-1)(x-5)$$
よって、\(x=1,5\)のとき放物線と直線は交わる。
\(x=1\)のとき、\(y=2\)
\(x=5\)のとき、\(y=6\)
よって交点は、\((1,2),(5,6)\)





二次関数の変形まとめ


まとめ
- グラフを描く・軸を求める・座標を求めるためには、平方完成形にすれば良い。
- \(x\)軸との交点を求めるためには、因数分解形にすれば良い。
- 計算をする時は、一般形にするといいことが多い。
むやみやたらに、適当な変形をしても、不必要な情報だけが集まるだけ。
次第に自分が何をしたいのか、何を求めればいいのか分からなくなってしまいますよ。
問題を見て、解答のためには何の情報が必要なのか、よく考えた上でこれらのツールを使うようにしましょう。
以上、「二次関数 よくある変形について」でした。
チェック問題
例題
点\((2,-3)\)を頂点とし、点\((4,-7)\)を通るような放物線の方程式を求めよ。


求める二次関数の方程式を\(y=a(x-p)^2+q\)とする。
頂点が\((2,-3)\)なので、\(y=a(x-2)^2-3\)となる。
点\((4,-7)\)を通るので、これに代入して\(a\)を求めれば良い。


\(x=4,y=-7\)を代入すると、
$$-4a=-4$$
$$a=-1$$
よって\(y=-(x-2)^2-3\)
例題
二次関数\(y=\frac{1}{2}x^2-x+1\)の最大値、最小値があれば求めよ。




これは頂点\((1,\frac{1}{2})\)、下に凸のグラフを描く。
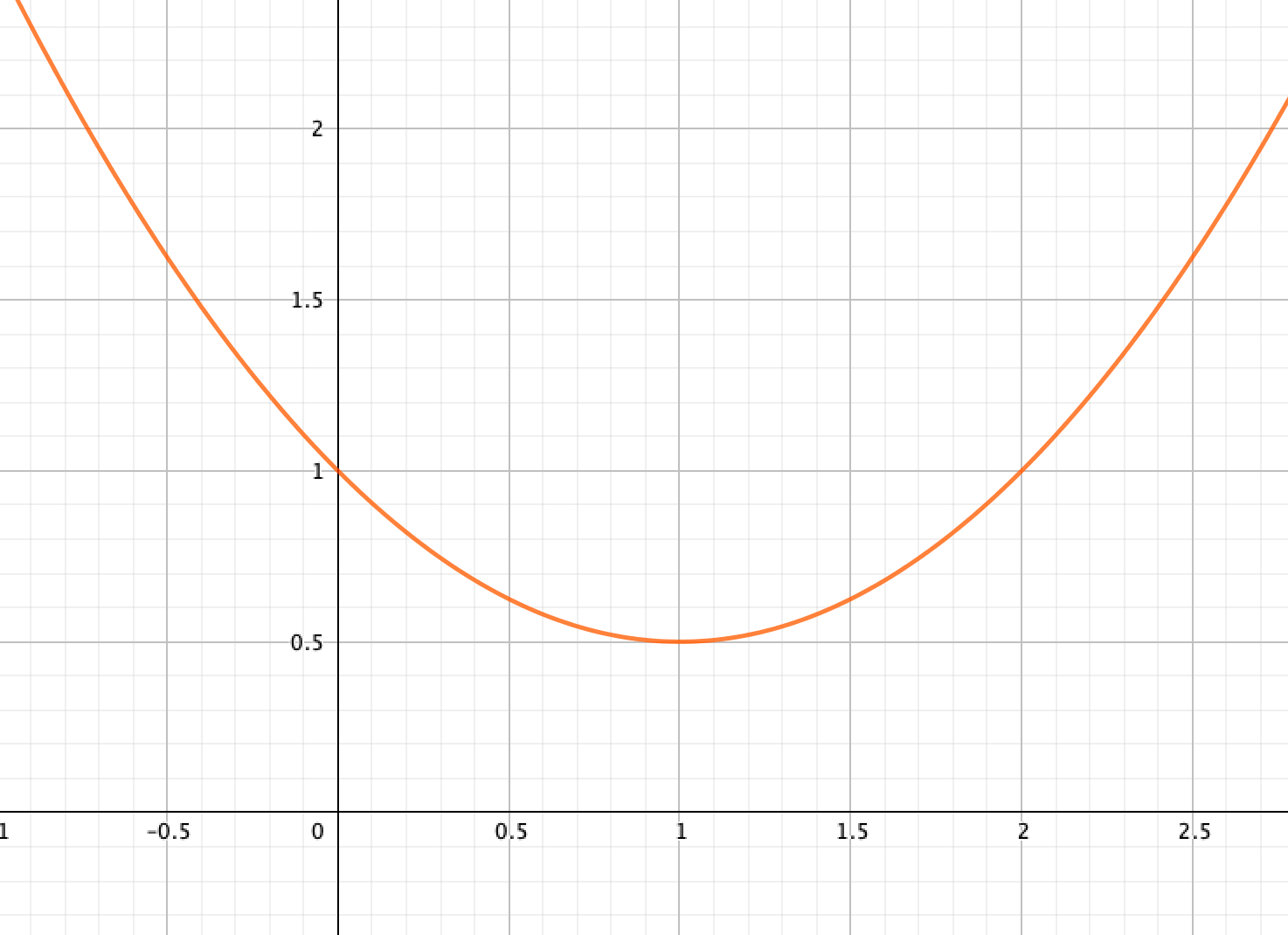

よって
- 最小値\(\frac{1}{2}(x=1のとき)\)
- 最大値なし









