【和集合・共通部分・補集合】それぞれの違いと捉え方、使う場面を徹底解説

楓

これまで集合と要素の関係、集合と集合の包括関係について見てきたね。

今まで難しく感じてたけど、だんだん要点がわかってきたよ！

小春

楓

じゃあ今日は集合の中でも重要な3つの集合を見てみよう！

この記事を読むと、この問題が解ける！

全体集合\( U = \left\{ x | xは20以下の自然数 \right\} \)に対して2つの集合
$$A = \left\{ 2, 3, 6, 7 \right\}$$
$$B = \left\{ x | xは20以下の素数 \right\}$$
を考える。このとき、次の集合に含まれる要素を全て書き表せ。

1. \(A \cap B\)
2. \(A \cup B\)
3. \(\overline{A \cup B}\)

楓

答えは一番最後に扱うよ！

共通部分

1〜12のうち、2の倍数だけを集めた集合\(A\)と、3の倍数だけを集めた集合\(B\)を考えます。

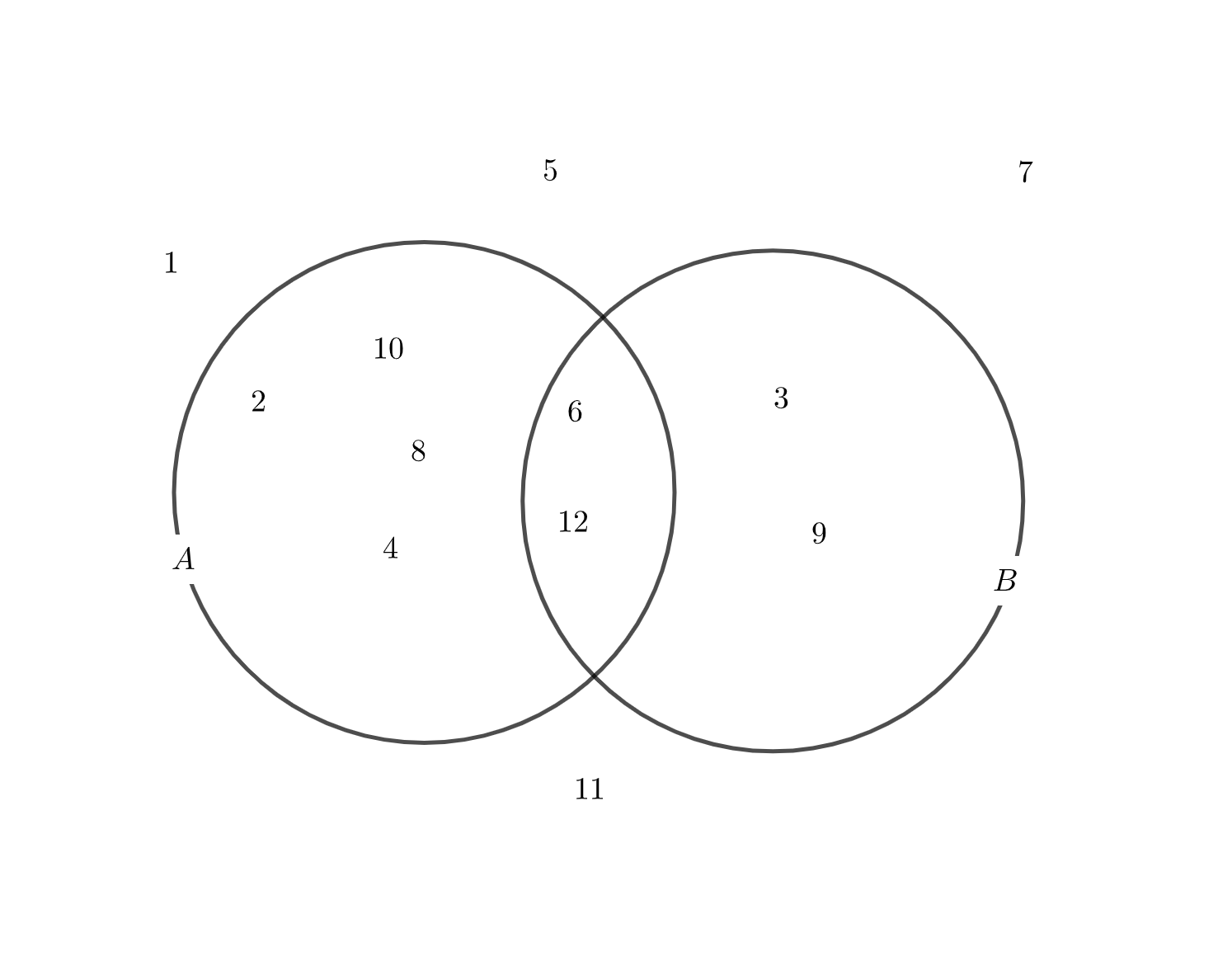
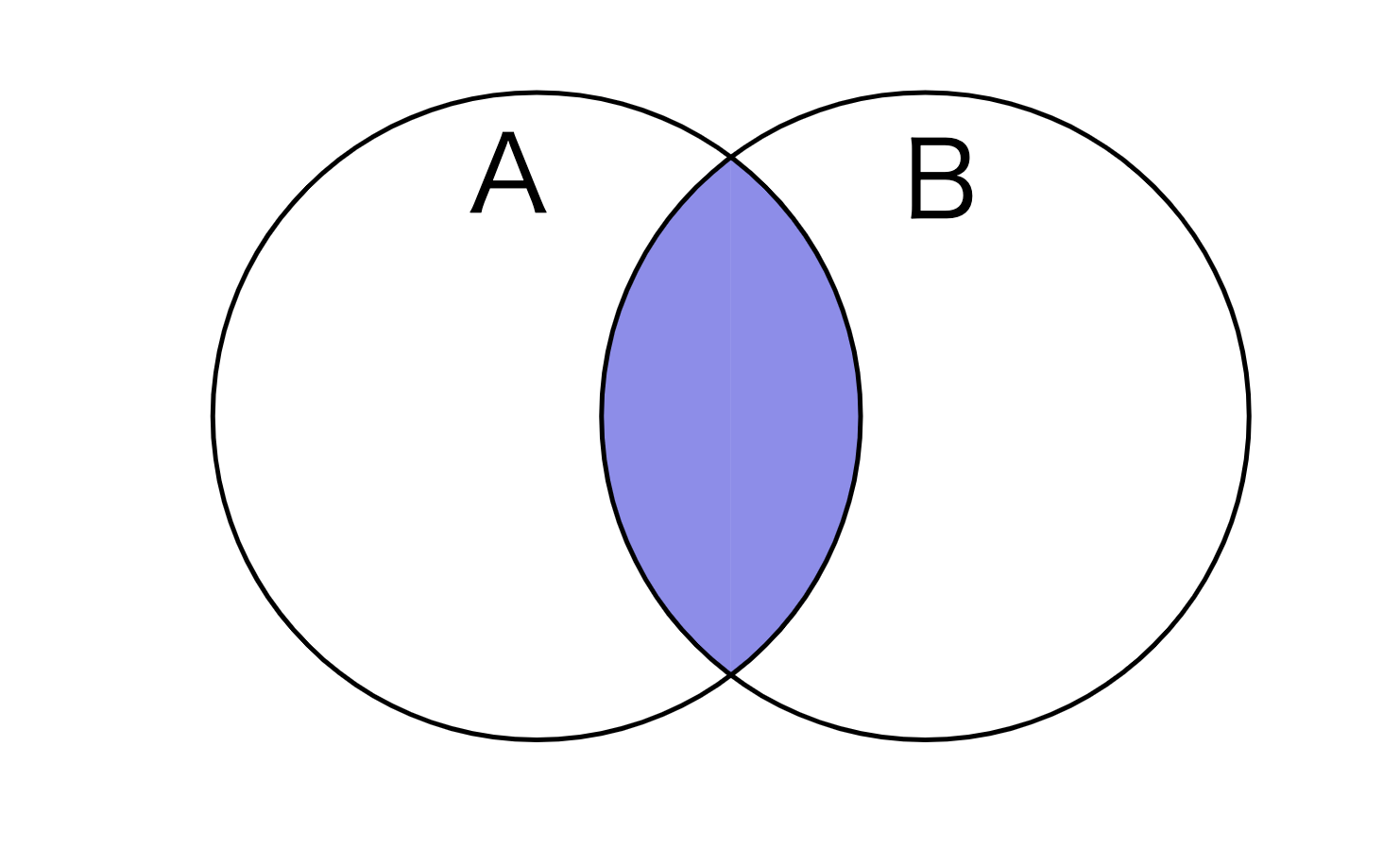
このとき、集合\(A\)にも含まれ、かつ集合\(B\)にも含まれている要素がありますね？

小春

6と12のことかな？

このような\(x \in A\)かつ\(x \in B\)の要素だけ集めて作った集合を共通部分といいます。

楓

つまり集合\(\left\{ 6, 12 \right\}\)のことを共通部分というってこと！

集合\(A\)と\(B\)の共通部分は\(A \cap B\)と表され、\(\cap\)は蓋を閉じるようなイメージからキャップと読みます。

$$A \cap B = \left\{ x | x \in A かつ x \in B \right\}$$

和集合

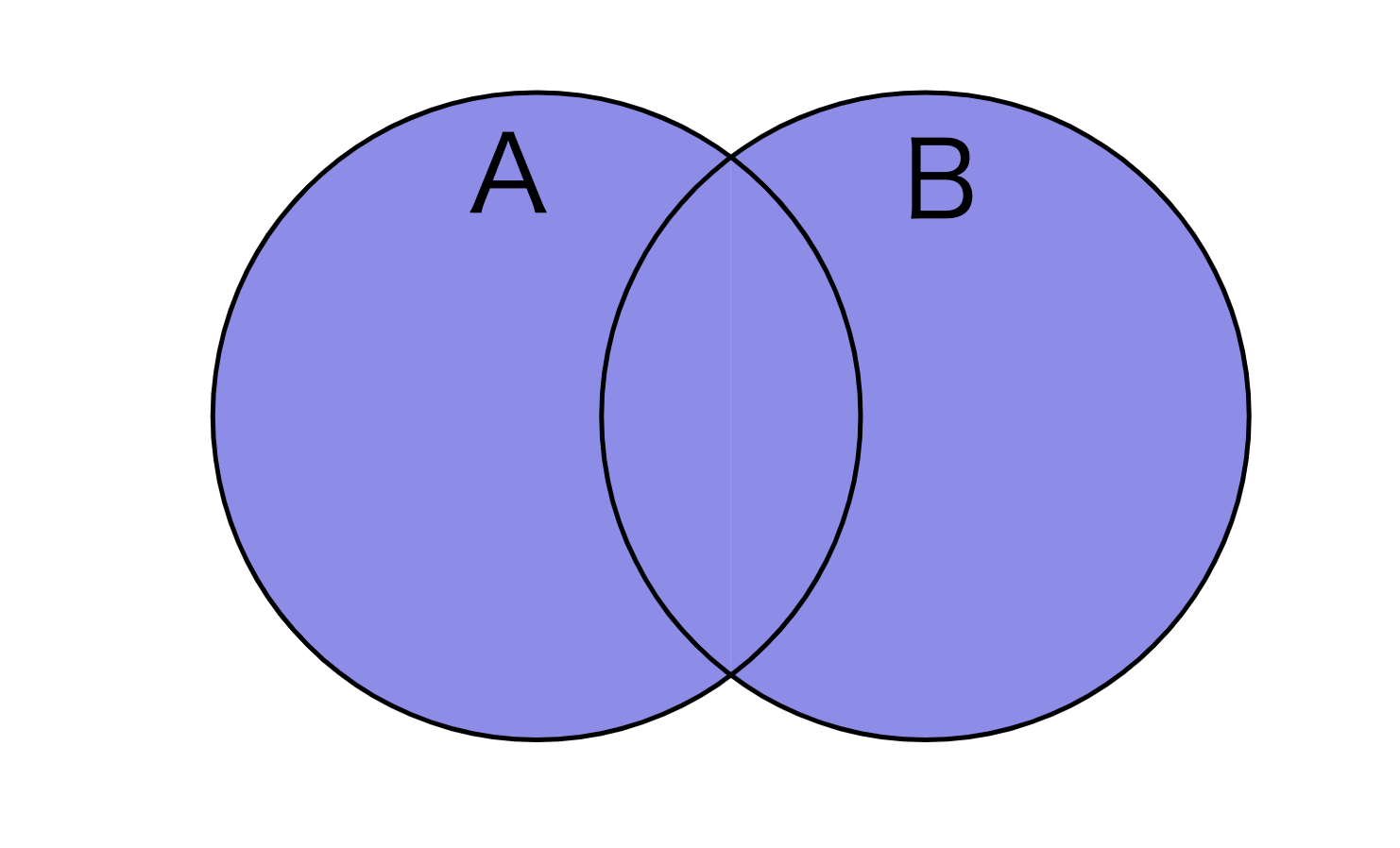
先程と同じ2つの集合を考えてみましょう。

このとき、集合\(A\)か集合\(B\)、少なくともどちらか一方には含まれている要素を考えます。

小春

す、少なくとも・・・？

つまり最低レベルの条件として\(A\)か\(B\)に含まれているってことだね。

楓

小春

じゃあ、6や12みたいに\(A, B\)どっちにも含まれる要素もOKってこと？

その通り。\(A, B\)どちらかに含まれていればOKってことは、どちらにも含まれているものもOKってことだよ。

楓

小春

ということは\(2, 3, 4, 6, 8, 9, 10, 12\)が該当するね。

このような\(x \in A\)または\(x \in B\)の要素だけ集めて作った集合を和集合といいます。

楓

つまり集合\(\left\{ 2, 3, 4, 6, 8, 9, 10, 12 \right\}\)のことを和集合というってこと！

集合\(A\)と\(B\)の共通部分は\(A \cup B\)と表され、\(\cup\)は容器のようなイメージからカップと読みます。

$$A \cup B = \left\{ x | x \in A もしくは x \in B \right\}$$

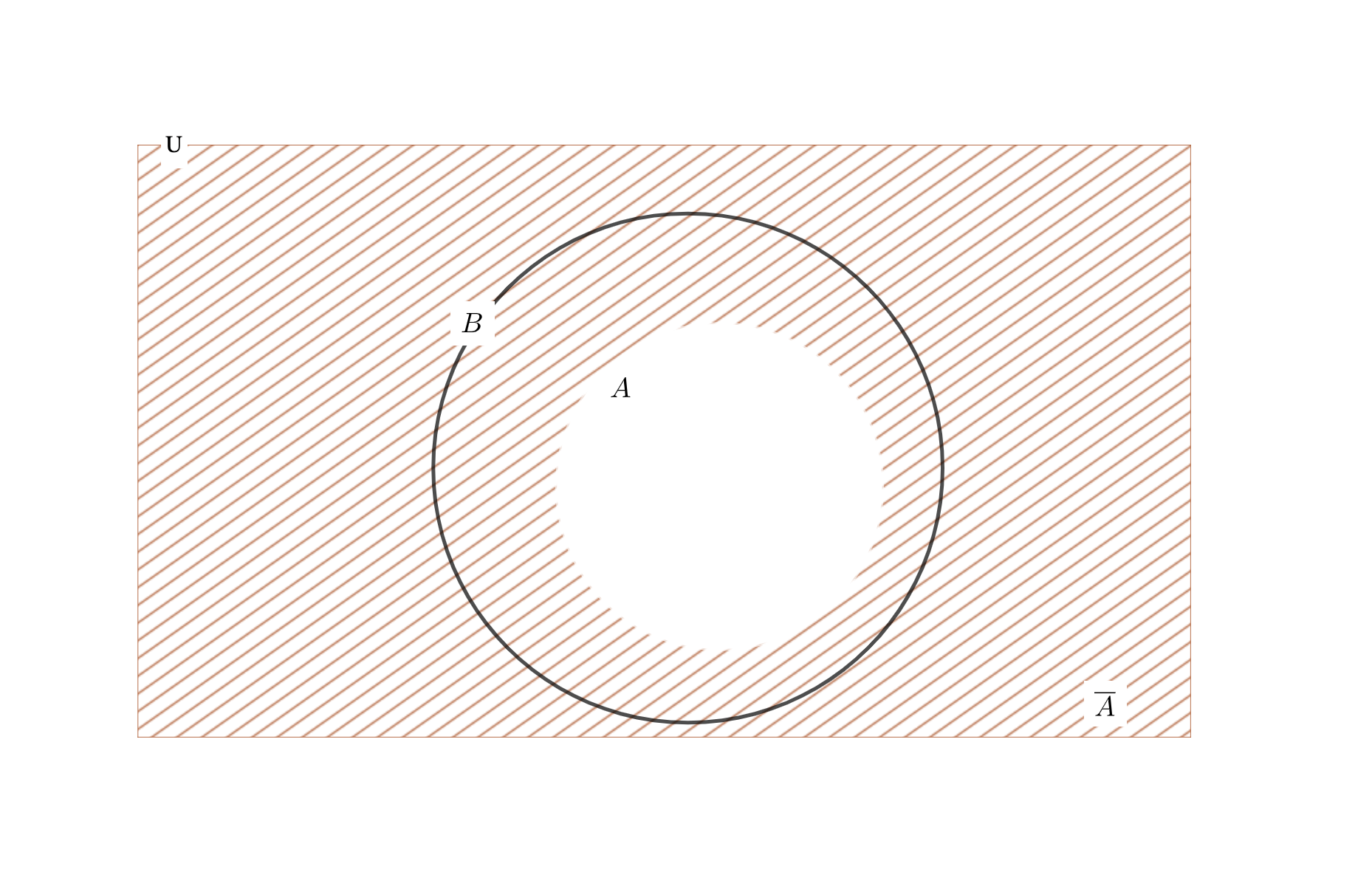
補集合

これまで個別に集合\(A\)や\(B\)を捉えてきましたが、実際の場面では1つの集合\(U\)を決めて、その部分集合として\(A, B\)を考えることが多いです。

この集合\(U\)を全体集合といい、集合\(U\)の要素で集合\(A\)には含まれない要素全体の集合を\(\overline{A}\)と表します。

図で表すと次のようなイメージをしています。

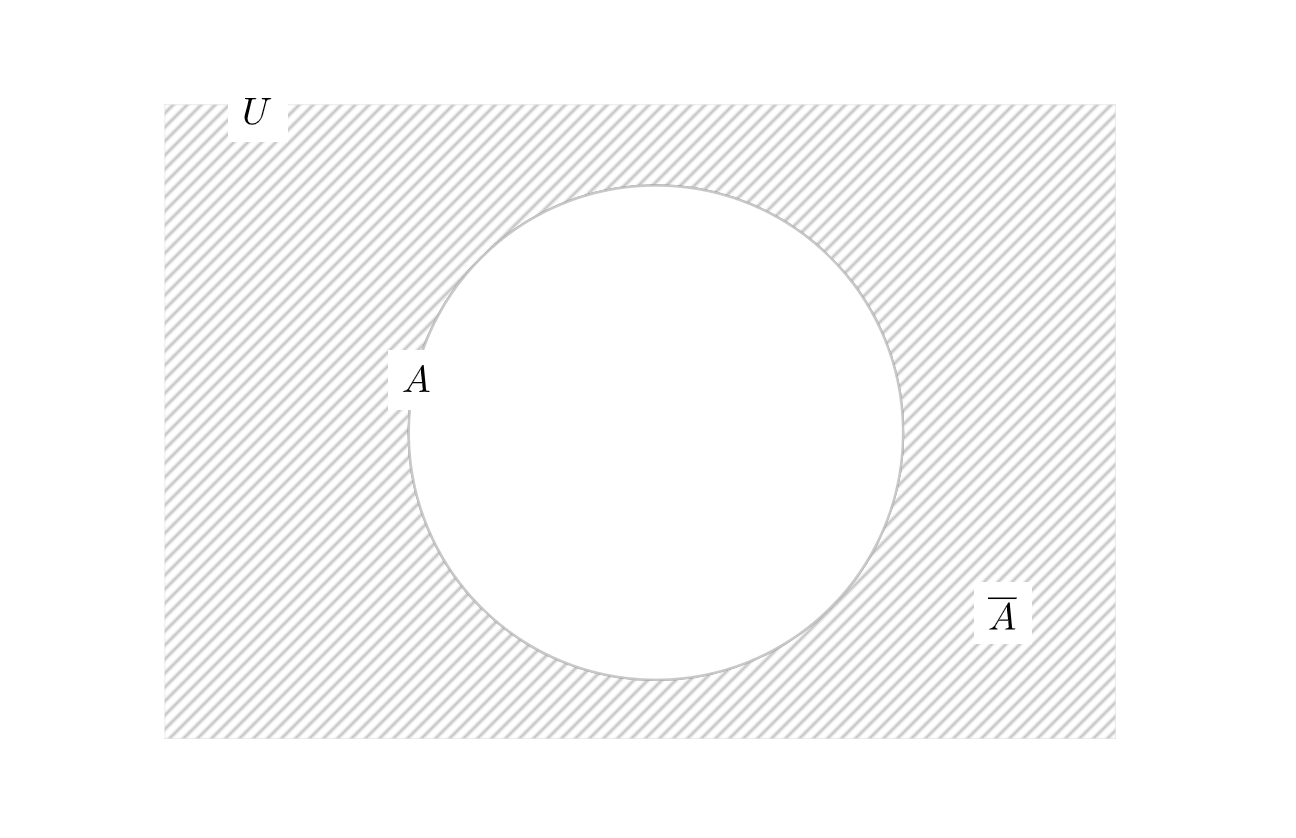
例えば、全体集合

に対して、2の倍数を集めて作った集合

を考えると、その補集合は

となります。

$$\overline{A} = \left\{ x | x \notin Aかつx \in U \right\}$$

補集合の性質

この定義とベン図を見てもらうと、次のような性質がわかります。

上から順に日本語訳していくと、

となります。

小春

確かに定義とベン図から明らかだね。。。

まとめ

楓

それじゃあまとめよう！

今回扱った集合間の関係は、今後数学を捉える上で非常に重要な内容になります。

イメージで覚えるのも大事ですが、まとめにもある式で理解しておくことが肝心です。

楓

例えば、「\(x \in A \cap B\)は\(x \in A\)かつ\(x \in B\)を満たす要素を集めた集合だ」と捉えられるようにしておこう！

ベン図で理解することは悪いことではありませんが、集合の話は抽象的になりすぎて、ベン図で書くことが難しいことがちょいちょいあります。

そのため、集合を「どんな要素の集まりなのか」で捉えられておくようにしておくと良いですよ。

以上、「和集合・共通部分・補集合について」でした。

チェック問題

とりあえず、集合\(B\)の全要素は書き出せるのでメモっておきましょう。

\(A \cap B\)は集合\(A, B\)の共通部分を表す集合のことでしたね。

\(A\)にも\(B\)にも含まれている要素を考えると、\(2,3,7\)が該当しますね。

続いて\(A \cup B\)は集合\(A, B\)の和集合のことでしたね。

\(A\)または\(B\)にも含まれている要素を考えると、重複しているものを除くと\(2,3,5,6,7,11,13,17,19\)が該当しますね。

よって

最後に\(\overline{A \cup B}\)を考えてみましょう。

これは\(A \cup B\)の補集合、すなわち

の要素を考えれば良いということになります。

全集合の条件より、20以下の自然数の中で

に含まれないものは\(1,4,8,9,10,12,14,15,16,18,20\)

よって

となります。