【ド・モルガンの法則】を使うコツ！複雑な集合関係もコレ一発！【証明付き】

楓

さて、集合論最終章へと突入！ド・モルガンの法則を扱うよ！

ふぇ〜、、、なんか教科書にマーカー引かされたなぁ。。。

小春

楓

ド・モルガンの法則は暗記しがちなんだけど、めんどくさい式を理解しやすくできる便利な法則なんだ

じゃあ今回は法則の中身だけじゃなくて、使う場面や便利な場面も教えて欲しいな！

小春

この記事を読むと、この問題が解ける！

$$U = \left\{ x| 1から12までの自然数 \right\}$$
$$A = \left\{ x| xは12の約数 \right\}$$
$$B = \left\{ x| xは8の約数 \right\}$$
であるとき、

• \(\overline{\overline{A} \cap B}\)を求めよ。
• \(\overline{\overline{A} \cap \overline{B}}\)の要素を全て列挙せよ。

楓

答えは例題と一番最後で扱うよ！

ド・モルガンの法則

ド・モルガンの法則ですが、その内容は共通部分・和集合の補集合についてです。

楓

つまり2つの集合の共通部分、和集合に対して、そこに含まれない要素に着目した法則ってことね。

楓

上のー（バー）を分割して\(\cap\)と\(\cup\)を入れ替えることができるってことだね

なるほど〜、、、だけどこれ何に使うの・・・？

小春

証明は一旦後回しにして、このド・モルガンの法則が有効活用できる場面を見て行きましょう。

ド・モルガンの法則　例題

ド・モルガンの法則より、

となるので、

より、

とわかりました。

普通に考えてみるとどうなるでしょうか。

を満たす集合を考えればOKですね。

そこでまず、\(\overline{A} \cap B\)の要素を考えてみることにしましょう。

ということなので、

の共通部分をとって

となります。

\(\overline{\overline{A} \cap B}\)はこの補集合なので、

となりますね。

以上のことから、ド・モルガンの法則には次のことが言えそうです。

楓

特に最後の特徴が大事で、要素を列挙するような具体的な解答は他の問題に何も応用できない場合が多いんだ。

ド・モルガンの法則はどんな集合でも使うことができるから、一度コツを覚えるとなんでも使ってOKってことね。

小春

楓

そゆこと！これからどんどん抽象的になっていく集合に対して、具体的に数え上げていくという原始的なアプローチは結構死に近いよ笑

【直感的】ド・モルガンの法則の証明

ド・モルガンの法則はベン図を使って証明することができます。

ここでは\(\overline{A \cap B} = \overline{A} \cup \overline{B}\)を示します。

楓

もう片方の法則も同様に証明できるよ。

\(\overline{A}\)の部分を見てみましょう。

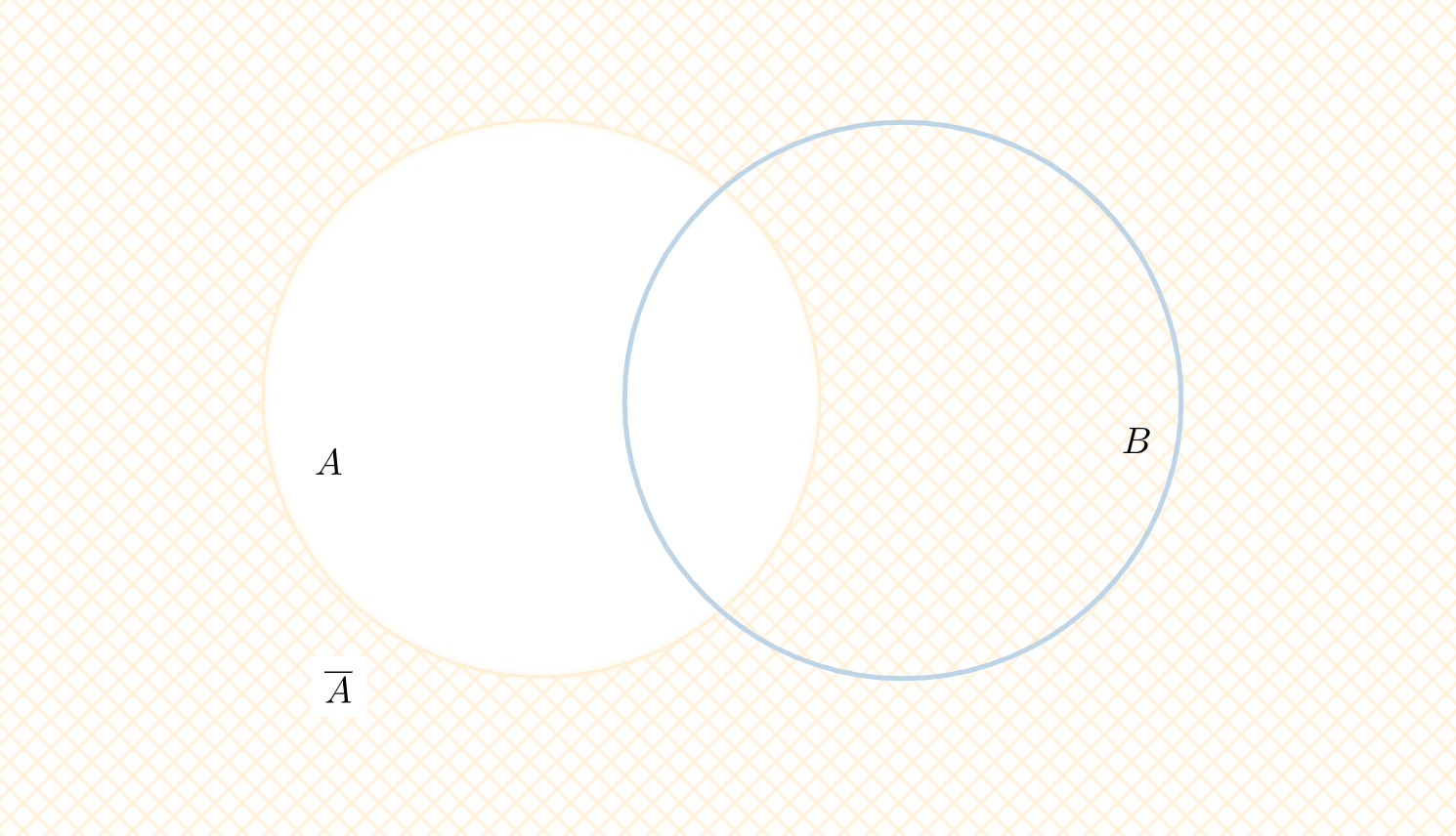
続いて、\(\overline{B}\)の部分を見てみよう。

楓

じゃあ\(\overline{A} \cup \overline{B}\)の部分はどこかな？

和集合を考えればいいわけだから、オレンジ線と青線の部分すべてだよね。

小春

小春

あっ、\(A \cap B\)部分以外全てを表してるっ！！！

その通り、つまり\(A \cap B\)の補集合は\(\overline{A} \cup \overline{B}\)と表すことができるんだね。

楓

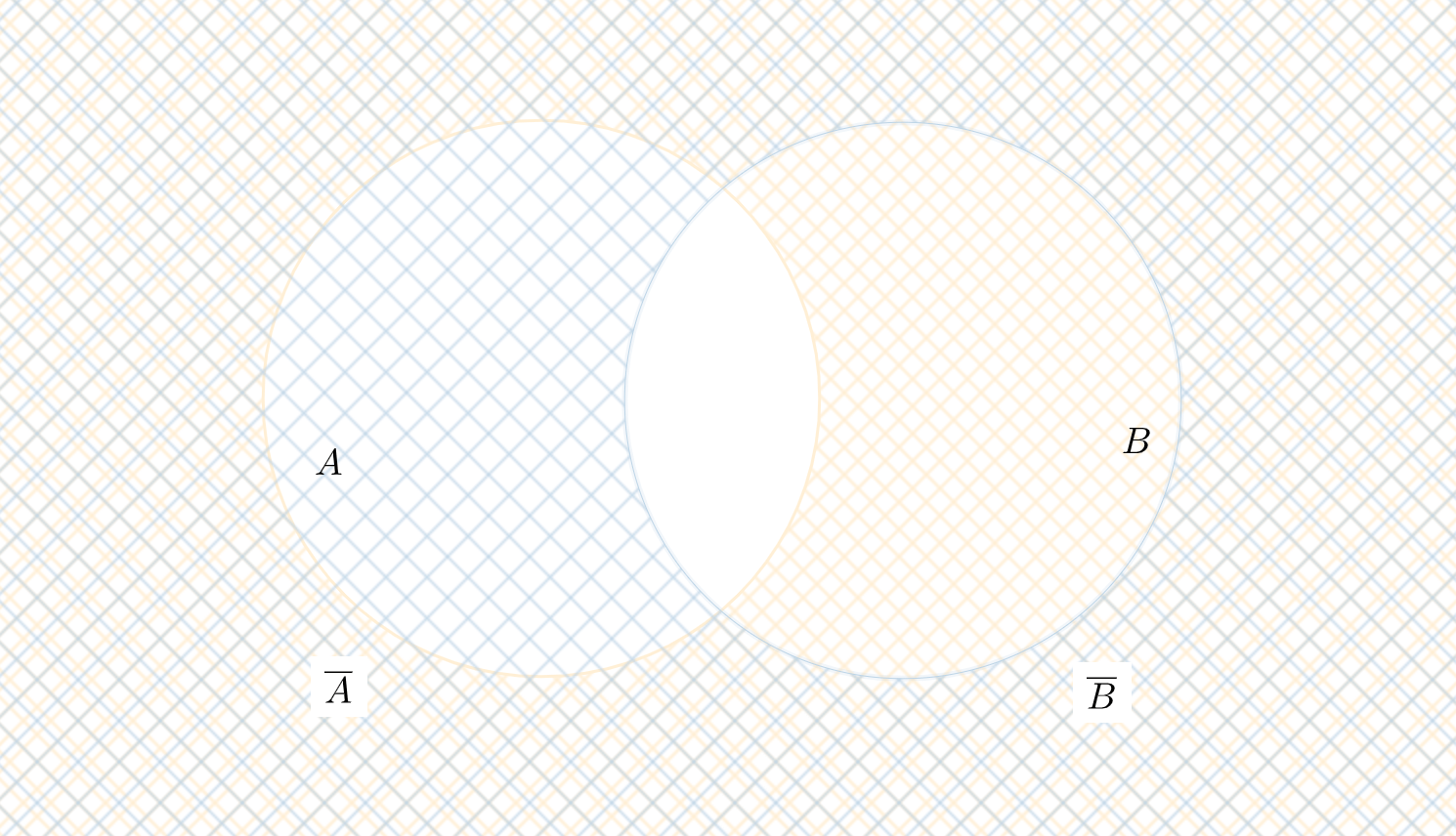
以上より

が証明できました。

【論理的】ド・モルガンの法則の証明

ド・モルガンの法則は論理式で証明しようとすると、少しコツが必要です。

また高校数学では、あまり論理的に証明させることは多くないです。

しかし「2つの集合が等しい」ということを証明するための基本的な手順の練習にはなると思いますので、お暇があればぜひご覧ください。

\(\overline{A \cap B} = \overline{A} \cup \overline{B}\)の証明

まず\(\overline{A \cup B} = \overline{A} \cap \overline{B}\)を示してみます。

以前、

ということを学びました。

参考【集合の包括関係・部分集合】部分集合の捉え方と等しい集合の条件を解説

また、

ということを学びましたね。

参考【集合の包括関係・部分集合】部分集合の捉え方と等しい集合の条件を解説

この2つを使って、次のように証明していきます。

•  
  STEP1
  \(\overline{A \cup B} \subset \overline{A} \cap \overline{B}\)であることを示す
  \(x \in \overline{A \cup B}\)ならば、\(x \in \overline{A} \cap \overline{B}\)であることを示せればクリア
•  
  STEP2
  \(\overline{A \cup B} \supset \overline{A} \cap \overline{B}\)であることを示す
  \(x \in \overline{A} \cap \overline{B}\)ならば、\(x \in \overline{A \cup B}\)であることを示せればクリア
•  
  STEP3
  \(\overline{A \cup B} = \overline{A} \cap \overline{B}\)を示す
  \(\overline{A \cup B} \subset \overline{A} \cap \overline{B}\)かつ\(\overline{A \cup B} \supset \overline{A} \cap \overline{B}\)であることに言及すればOK

STEP1 \(\overline{A \cap B} \subset \overline{A} \cup \overline{B}\)であることを示す

このポイントを抑えておくと、ここで証明すべきは

であるとわかります。

証明

\(x \in \overline{A\cup B}\)ならば、補集合の性質より\(x \notin A\cup B\)

つまり\(x\)は\(A, \ B\)の共通部分には含まれない。

ゆえに\(x \in \overline{A} \)かつ\(x \in \overline{B}\)

\(x\)は\(\overline{A}\)にも\(\overline{B}\)含まれるということなので、

$$x \in \overline{A} \cap \overline{B}$$

したがって、\(\overline{A \cup B} \subset \overline{A} \cap \overline{B}\)が示された。

STEP2 \(\overline{A \cap B} \supset \overline{A} \cup \overline{B}\)であることを示す

\(x \in \overline{A} \cap \overline{B}\)とすると、\(x \in \overline{A}\)かつ\(x \in \overline{B}\)

つまり、\(x \notin A\)かつ\(x \notin B\)

これはすなわち\(A, \ B\)どちらにも含まれないことを表すので\(x \notin A \cup B\)。

よって、\(x \in \overline{A \cup B}\)

以上より、\(\overline{A} \cap \overline{B} \subset \overline{A \cup B}\)が示された。

STEP3 \(\overline{A \cap B} = \overline{A} \cup \overline{B}\)を示す

上記STEP1、STEP2より、

となるので、

が示された。

\(\overline{A \cup B} = \overline{A} \cap \overline{B}\)の証明

もう一方の法則は、先程示した

から求めることができます。

適当な集合\(X,\ Y\)を考えても

が成り立ちますね。

両辺の補集合を考えると、

このとき、\(\overline{\overline{X \cup Y}} = X \cup Y\)なので、

ここで\(X = \overline{A},\ Y = \overline{B}\)とおくと、

まとめ

楓

それじゃあまとめよう！

集合論は、これから学んでいく数学の根幹となる重要な議論です。

その中でも複雑な集合関係を、別の視点から理解できるド・モルガンの法則の価値はとても高いもの。

法則自体は簡単なものですので、ぜひ有効活用してください。

以上、「ド・モルガンの法則について」でした。

チェック問題

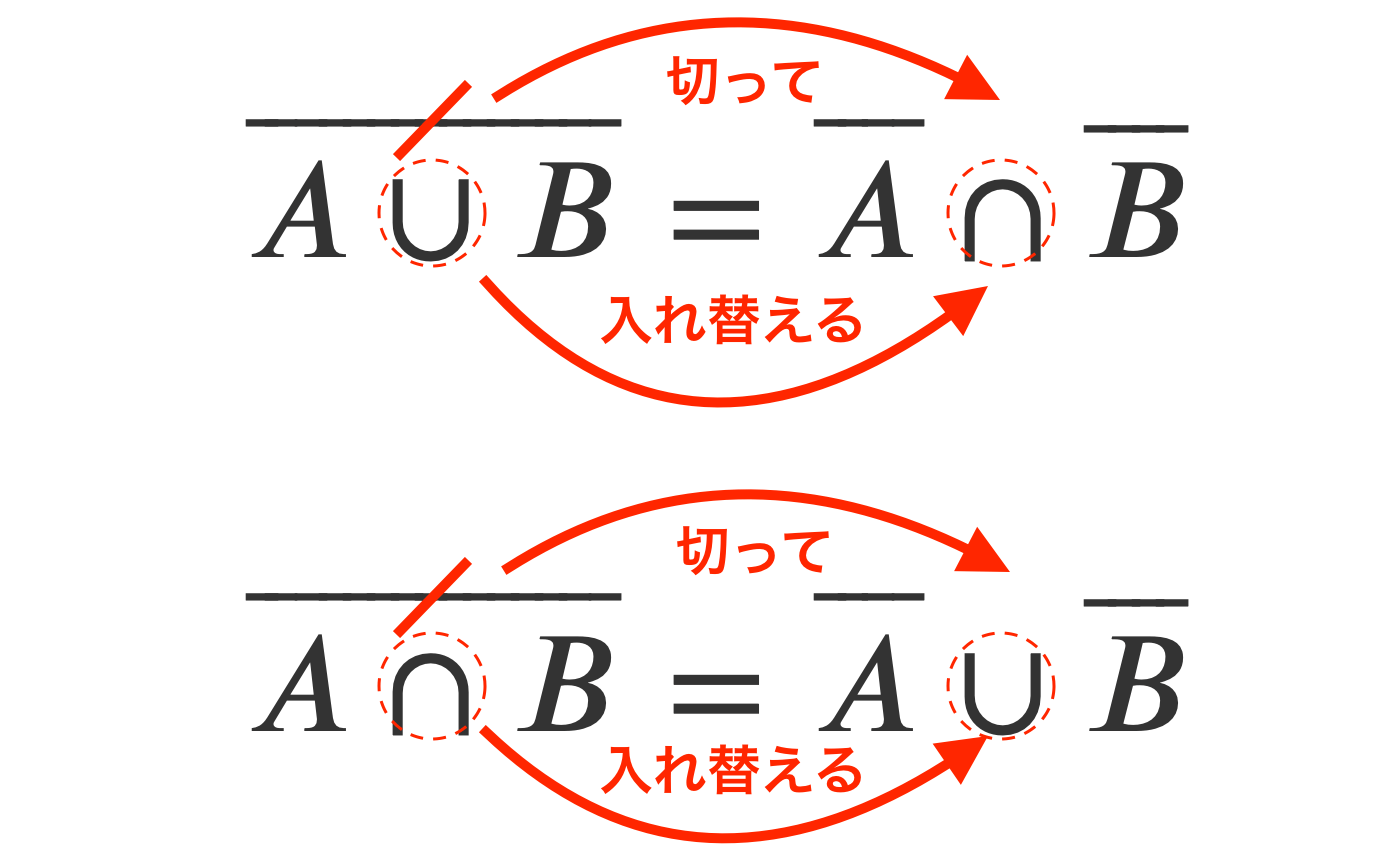
切って、入れ替える。

ド・モルガンの法則より、

$$\overline{\overline{A} \cap \overline{B}} = A \cup B$$

よって、集合\(A\)と集合\(B\)の和集合を求めれば良いので、

から、

となる。