【命題】が必ず理解できる4ステップ！真偽の基準と証明するテクニックを徹底解説！

 

 

 

数学における命題とは

 

「命題」とは、数学に限らず世間一般でも使われることのある言葉です。

意味にそれほど違いはありませんが、しっかり定義しようとすれば次のようになります。

 

例えば

は人や比較対象によって真偽が変わりますね。なので命題にはなり得ません。

 

では次の文章はどうでしょうか？

 

このように命題では、比較対象の\(x\)や7みたいな、大小関係や文字式などの条件が含まれることが多いです。

 

仮定と結論

数学では命題を記号で略記することが多いです。

 

具体例を見ていきましょう。

とします。

 

このとき、命題「\(x > 3\)ならば、\(x>1\)」は

と書くことができます。

 

またこの条件\(A\)のように\(\Rightarrow\)より前にある部分を仮定、条件\(B\)のように\(\Rightarrow\)より後ろにある部分を結論と言います。

 

数学における命題は必ずこの形で書くことができ、仮定が前提条件、結論が示すべきことがらとなっています。

 

例えば先程の具体例

を命題に直すと、

のようになります。

 

命題が真か偽かは命題の定義には含まれていないので、1、2のどちらも、真偽に関係なく命題となります。

 

【重要】仮定の考え方

命題を理解するためのポイントは仮定にあります。

 

突然ですが、命題が真であると認められるときはどういうときでしょうか？

 

答えられましたか？

数学がわからなくなる要因の1つに、何を示せば命題が真として認められるのか把握していないことが起因していることが多いです。

 

それでは答えを発表します。

 

具体例を通して見ていきましょう。

 

1では、仮定が\(99 > x > 1\)となっています。

このとき仮定を満たすすべての要素とは、\(99> x > 1\)を満たすすべての数になります。

 

そのため

のすべての数において、\(100 > x\)が認められればこの命題は真となるというわけです。

 

2では、仮定が\(x=7\)となっています。

これを満たすすべての要素、といっても7しかありませんね。

よって\(x=7\)が\(x  >11\)を満たしていればこの命題は真となるわけです。

 

数の集合を用いた前提条件

早速ですが、この命題は真でしょうか？

 

正解は命題になっていない、が答えです。

　

 

数学における数には自然数や整数、実数などの数の世界がありましたね。

参考【数の集合】自然数とは？整数とは？感覚だけでわかる数の集合

 

上の命題では、仮定における\(x\)がどの数の集合かが決められていません。

そのため、仮定が次のように数の集合によって変化してしまいます。

 

これはつまり、\(x\)を自然数として認識した人と整数として認識した人で結論が分かれることを意味します。

 

よって、上記を正しく命題として表記するのであれば

のように注釈を付け加える必要があり、略記で表すと

のように書く必要がありますね。

 

以上のことから、命題として成立させる上で

数の集合が重要な前提条件となる

ことがお分かりいただると思います。

 

反例

 

大事なことなので、もう一度掲載しておきましょう。

 

 

これはその通りで、仮定を満たすすべての要素を列挙して結論が成り立っていることを証明するのは難しい場合があります。

 

そこで考え方を変えて、偽であることを示すためにはどうすれば良いでしょうか？

 

答えは、

そしてこの「仮定で述べられる条件を満たした要素の中で、結論を満たしていない要素」のことを反例と言います。

 

 

反例を1つ示せば、その命題は偽となる

 

後ほど、練習問題でこの反例を実際に使ってみることにしましょう。

 

集合とのリンク

 

命題は、これまで扱っていた集合として捉えることもできます。

次の命題を考えて見ましょう。

 

 

実数全体の集合を全体集合\(U\)としたとき、仮定\(p\)を満たす数の集合\(P\)と、結論\(q\)を満たす数の集合\(Q\)とします。

 

命題が真の場合の集合関係

命題\(p \Rightarrow q\)が真の場合とは、仮定を満たすすべての要素が結論を満たすことでした。

これを集合で捉えると、

となります。

 

そしてこれは「集合\(P\)が集合\Q\)の部分集合である」の定義とそのまんま一致しています。

参考【集合の包括関係・部分集合】部分集合の捉え方と等しい集合の条件を解説

 

つまり、

 

命題が偽である場合の集合関係

では命題が偽の場合はどうでしょうか？

真の場合とは反対に、

 

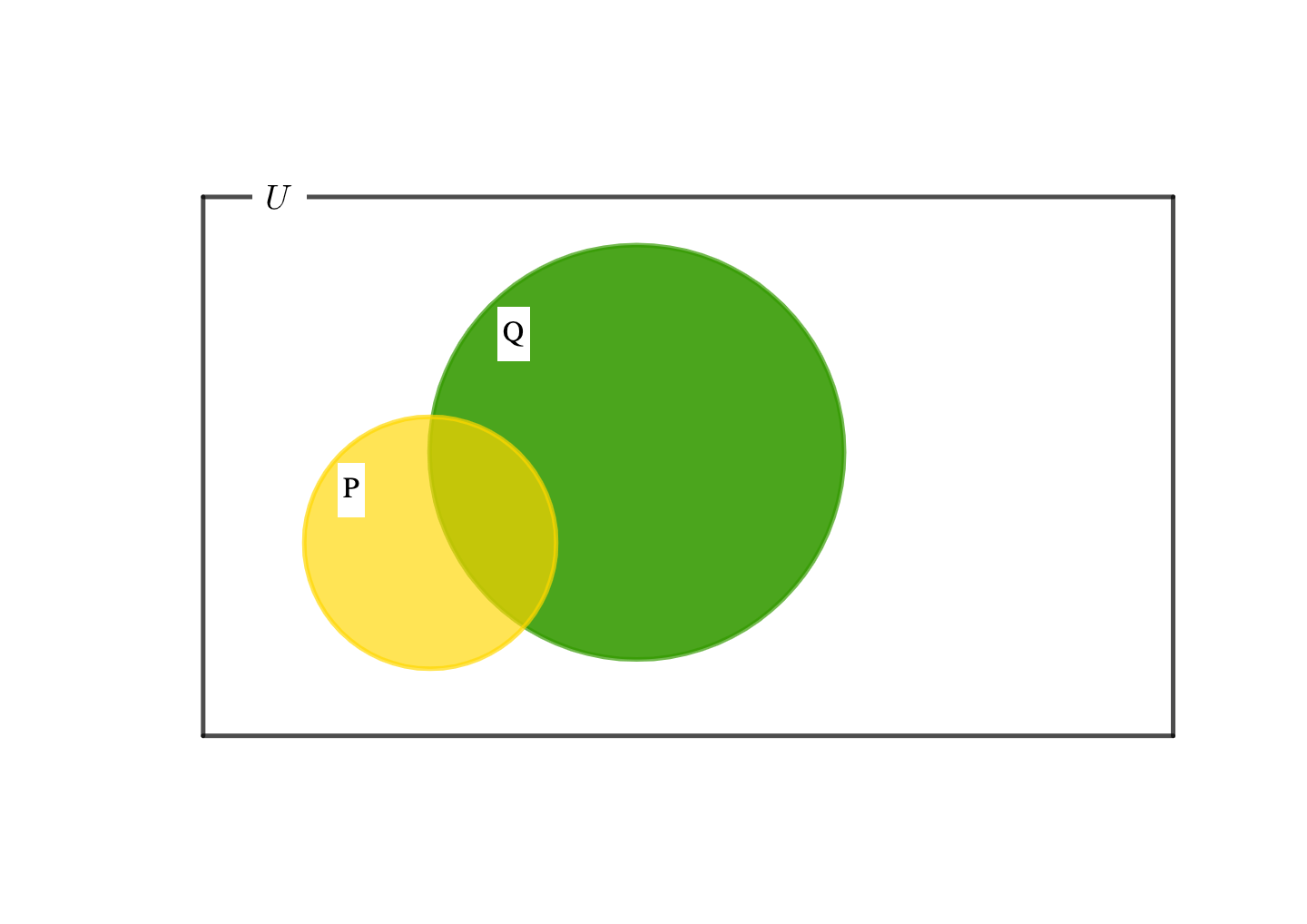
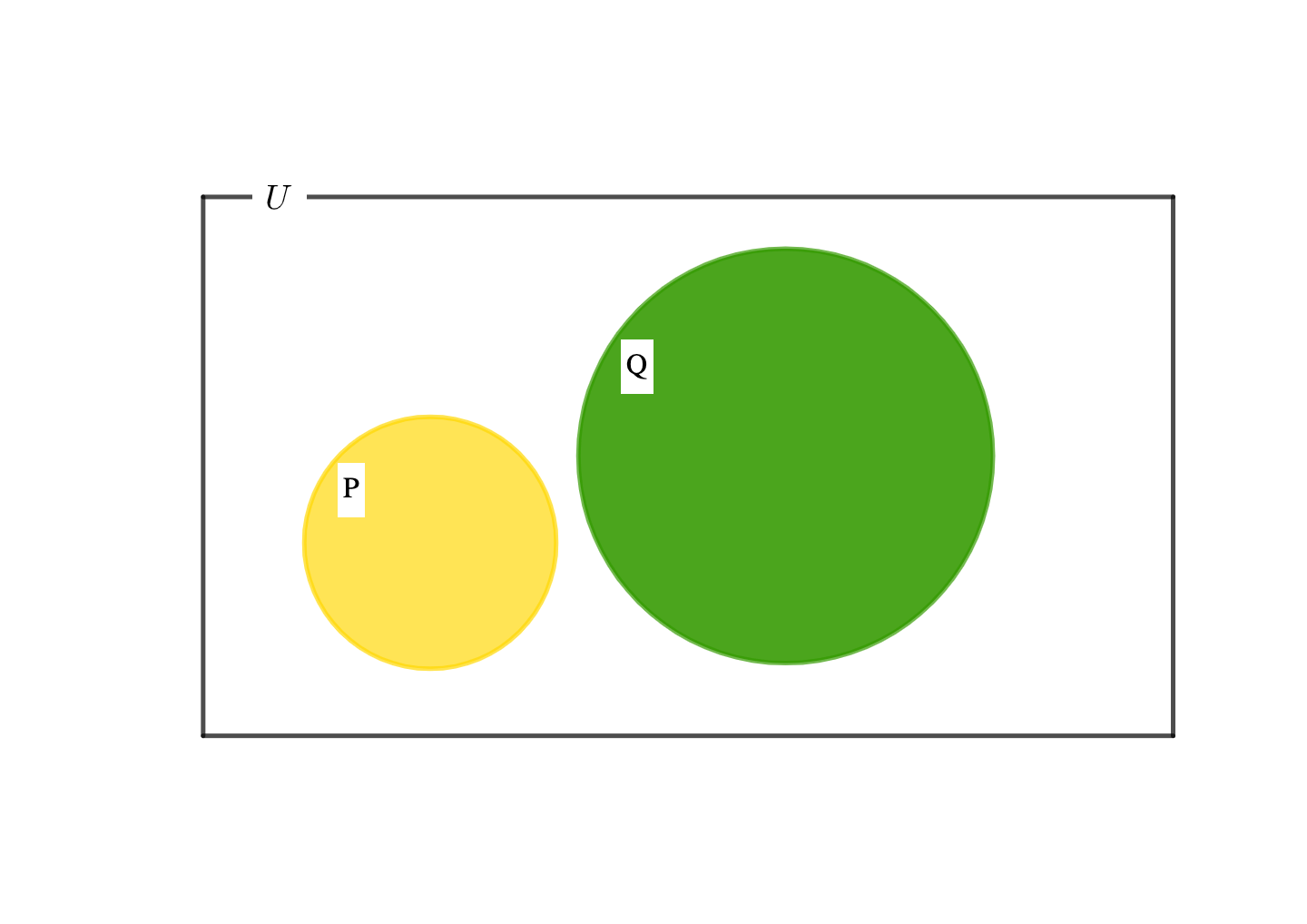
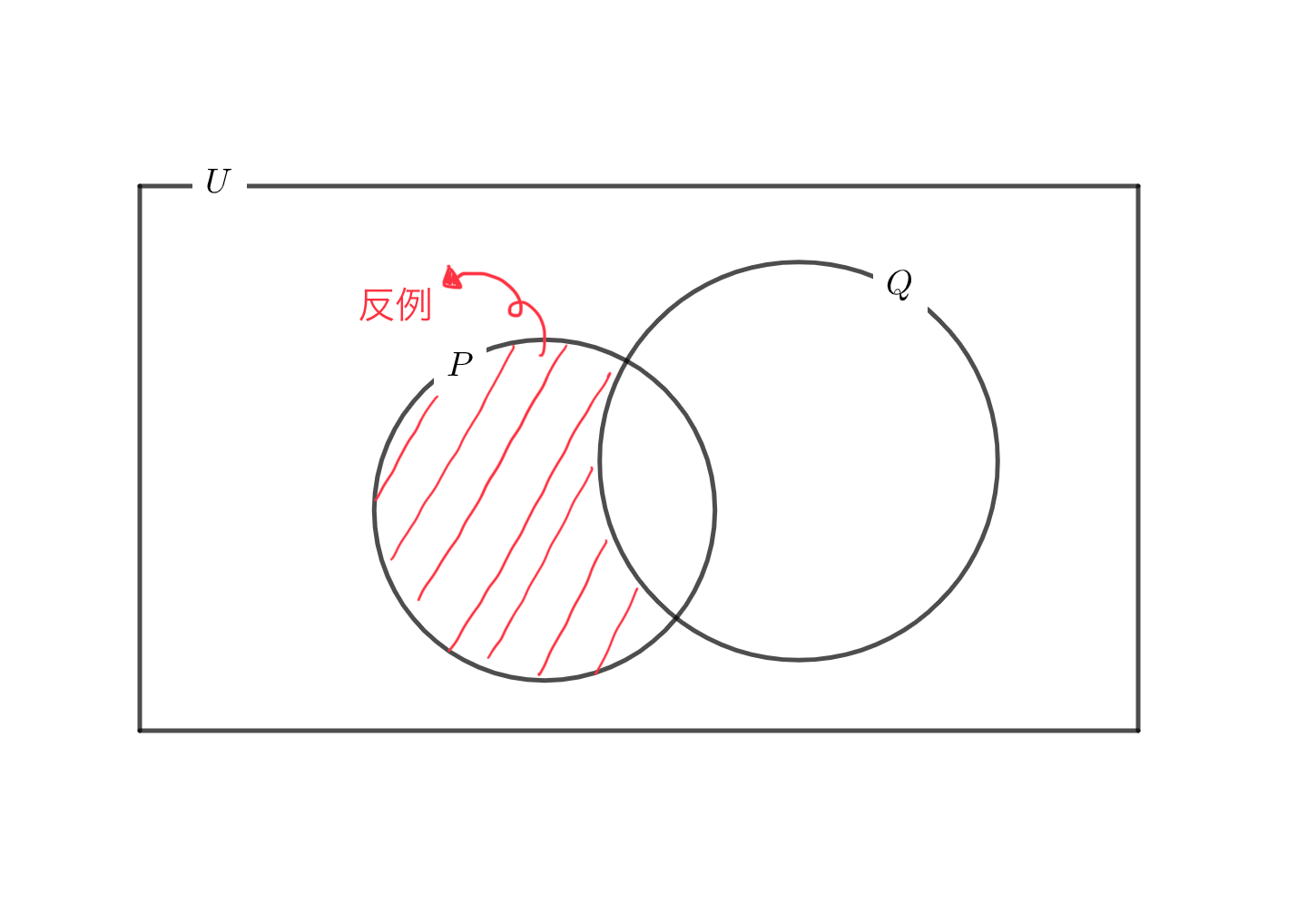
特に最初の集合関係にあるとき、\(x\in P かつx \notin P\cap Q\)に含まれる要素たちが反例と言われるわけです。

 

【命題の捉え方】真or偽を示す極意

 

命題は、数学における問題文と言っても過言ではありません。

命題を理解できなければ、数学の問題を理解していないことになるので、証明をはじめとして様々な問題が難解となります。

 

そんな基礎的な命題ですが、コツを掴めば特に気負う必要もなく、また証明問題では何を論点として証明を展開すればいいかが鮮明になります。

 

ここからは命題の真偽を証明するための考え方を見ていきましょう。

やることは次の3ステップです。

 

•  
  STEP1
  命題の仮定と結論を把握し、略記に直す
  日本語で表された文章を、数学の命題として考えやすいように略記に直してみます。
•  
  STEP2
  仮定の要素を考えてみて、全ての要素を列挙できるか考える
  仮定を満たす要素を、もれなくダブりなく列挙できるか考えてみましょう。
•  
  STEP3
  仮定の条件から式変形して、結論の式に持っていけないか考えてみましょう。
  仮定を満たす全ての要素が列挙できない場合、条件式を式変形することで結論の式と一致することが示せないか考えましょう。
•  
  STEP4
  全ての要素について証明できないなら、反例を考える
  上記までで仮定が結論を満たしていると証明できない場合、反例をあげられないか考えてみましょう。

 

命題　練習問題

それでは例題を通して、上記4ステップを身につけてみましょう。

 

問題1

 

step
1略記に直す

「〜を満たせば」の部分が仮定、「〜である」の部分が結論

 

 

step
2仮定を満たす全ての要素を列挙できるか

今回の場合、列挙していると実数全てを列挙しないといけなくなります。

そんなこと不可能ですね。。。

 

そこで仮定の式を、結論に向けて式変形できるか試みます。

 

step
3仮定の式を変形して、結論の式と一致させられるか

先に説明しておくと、仮定の条件だけで行う式変形は、仮定の式と同じ要素を指し示します。

 

つまり

ということです。

 

今回の場合、

を満たす実数\(a, b, c\)は、両辺に\(-b\)を足した

も満たします。

 

そしてこれはまさしく、結論の式

になりますねっ！

 

step
4反例を考える

今回はすでに証明できたので、このステップはいりません。

 

問題2

 

 

step
1略記に直す

 

step
2仮定を満たす全ての要素を列挙できるか

全ての実数と整数の組み合わせを列挙するのは不可能です。

次のステップにいきましょう。

 

step
3仮定の式を変形して、結論の式と一致させられるか

今回の場合、仮定の条件が少ないのでかなり難しい戦いになります。

 

\(a>b\)の式変形としては、\(a-b>0\)や\(-a-b<-2b\)などがありますが、結論の\(a^n > b^n\)に持っていくのは、厳しいです。

そこで見方を変えて、反例があげられないか考えましょう。

 

step
4反例を考える

実数\(a,\ b\)と正の整数\(n\)の組み合わせで、仮定は満たしつつ、結論を満たしていないものを探していきましょう。

もう一度言いますが、反例は1つ示せればその命題が偽であることを示していることになります。

 

例えば\(a=1, b=-3, n=2\)のときを考えてみましょう。

このとき\(a > b\)はしっかり満たしていますね。

ところが、結論の式に当てはめてみると、\(1^2 > (-3)^2\)となり、これは\(1>9\)となるため正しくありません。

 

つまり仮定を満たす条件\(a=1, b=-3, n=2\)は、結論が成立しない反例となるわけです。

 

日常生活での命題

ちょっとだけ脱線した内容を書きますね。

疲れた方は読み飛ばしてください。

 

この命題の理解は、論理的に人の話を理解する力を圧倒的に高めてくれます。

つまり日常生活で最も役立つ数学の分野と言っても過言ではありません。

 

社会を見渡してみると、多くの人が騙されている胡散臭い広告なんかがたくさんあります。

 

「あなたは私の親友よ。だから私はあなたを裏切るはずないわ！（だからこの書類に印鑑を・・・）」

「この仕事は社会に何も貢献できてない。つまりこの仕事をしている人は無意味な人だ。」

「私は人が好きです。だからこのビジネスを始めてあなたがお金持ちになることで、私も幸せです。」

などなど。。。

 

これらを命題にしてみるとどうでしょう。

反例を挙げること、できませんか？？

 

では3つ目はどうでしょう。。。

「あなたと私の幸せは違うでしょう？例えば私が殺しに快感を覚える殺人鬼であなたの前で人を殺してもあなたは幸せなの・・・？」

 

一般的に命題は、仮定の範囲が大きくなるほど反例が出やすくなります。

 

例えば

「女性たちは皆、身長の高い男性と結婚したい」

という命題は、世界中探せば身長の低い人と付き合っている方（反例）はたくさんいますね。

 

しかし範囲を限定した

「私の友達の女性たちは皆、身長の高い男性と結婚したい」

であれば、その人の友達全員を調査すれば真であると示せます。

 

何が言いたいかというと、論理的に説明しているように見えて実は

などのポンコツ理論が押し付けられることはよくあります。

なので人の話は信じる前に、よく聞いて反例がないかを考えてみてください。

 

まとめ

 

 

 

命題は数学の根幹であり、問題文とも言える部分。

どんなにあなたが正しいと思っても、反例が示せたり、仮定から導けないのであれば、その結論は間違っていることになります。

 

以上、「命題について」でした。

 

チェック問題

 

 

step
1略記に直す

 

step
2仮定を満たす全ての要素を列挙できるか

仮定の\(a, b\)は実数を表しているので、全数を列挙して示すのは無理。

 

step
3仮定の式を変形して、結論の式と一致させられるか

\(a>0,\  b>0\)のとき、\(a+b -2\sqrt{ab}\)について考えることができる。

 

実数において、2乗されたものは必ず正となるので

 

よって

となり両辺に\(\frac{1}{2}\)をかけると

となり結論と一致する。

step
4反例を考える

このフェーズはいりません。

 

 

step
1略記に直す

 

 

step
2仮定を満たす全ての要素を列挙できるか

仮定の\(a, b\)は実数を表しているので、全数を列挙して示すのは無理。

 

step
3仮定の式を変形して、結論の式と一致させられるか

 

 

ここで仮定の条件より、

より、\(\frac{b-a}{ab} < 0\)となる。

 

よって、\(\frac{1}{a} - \frac{1}{b} < 0\)より、

 

step
4反例を考える

このフェーズはいりません。