Today's Topic
集合を定義するためには、必ず「この要素は集合に含まれるか」が判別できるようなルールが必要となる。
(含まれるかもしれないし、そうじゃないかもみたいなのはNG)





この記事を読むと、この問題が解ける!
- ある集合\(A\)の要素は全て7以上16未満の偶数である。このとき集合\(A\)を表せ。
- $$B =\left\{ 3k | kは20以下の素数 \right\}$$と定義される集合\(B\)の要素を全て書き表せ。

【大事な考え方】集合とは
数学における「集合」は、範囲がはっきりしたものの集まりを指します。
範囲、というのは
- 「これはこの集合に入っている」
- 「これはこの集合に入っていない」
と、きっちりかっちり絶対に区別できるような、境界線ルールが存在することを指します。

例えば、次のようなものは集合にはなりません。
- 美味しい食べ物
- かわいい動物
なぜなら、「美味しいかどうか」や「かわいいかどうか」といった感覚によるものは境界線ルールにはなっていないからです。


数学ではこのような感覚を廃し、誰がどう読んでも理解される内容が一致するように境界線ルールを作り上げました。
例えば、
- 1以上7以下の奇数
- \(2x+1 > 4\)を満たす100未満の素数
という境界線ルールは、しっかり集合を定義することができます。

集合と要素の関係・表し方
要素とベン図
集合とは、ある境界線ルールによって集められたものの集まりのことでした。
このとき、集められた1つ1つのものを要素といいます。
また、ある数\(x\)がある集合\(A\)の要素であるとき、\(x\)は集合\(A\)に属する(含まれる)と言ったりします。
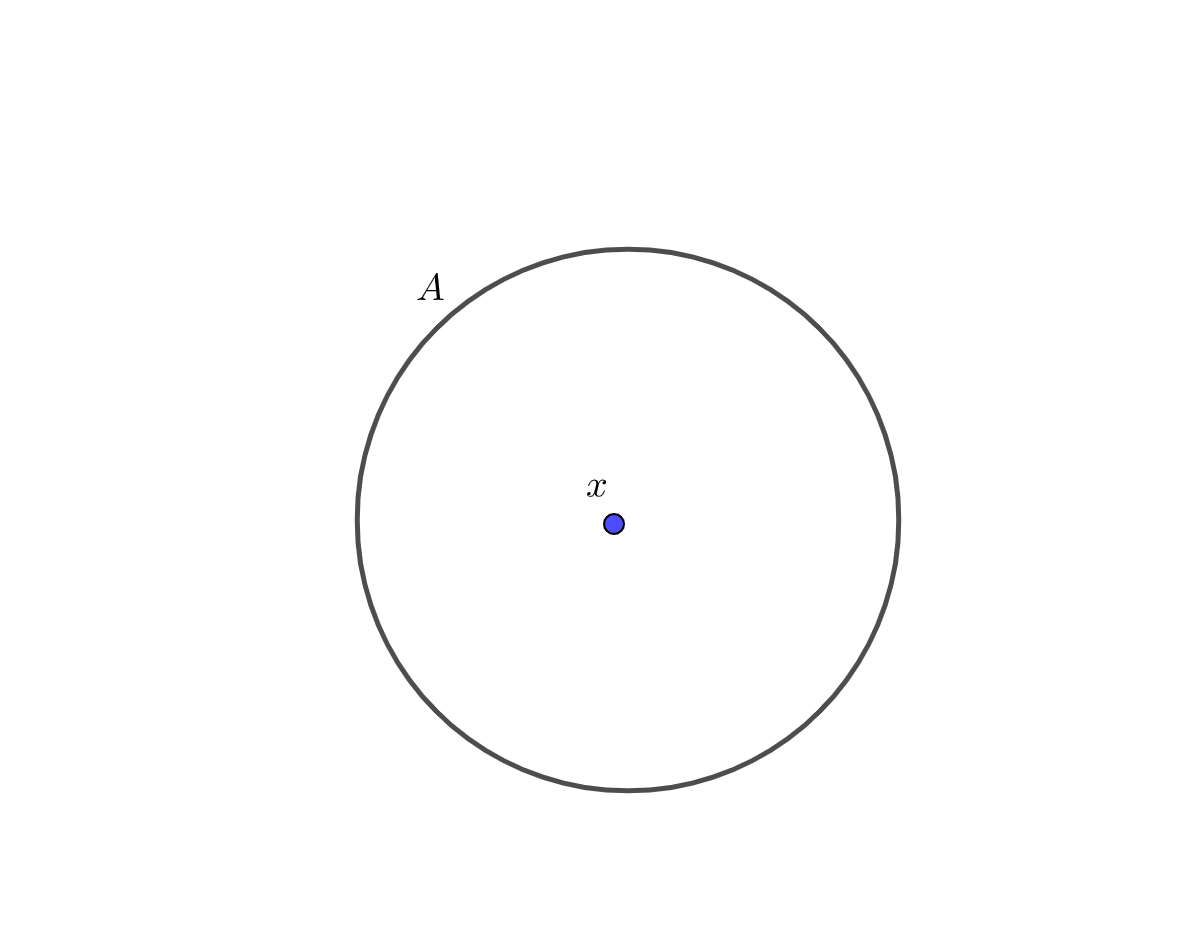


ただこの図を毎度回答用紙に書いていると紙がもったいないので、数学では
ポイント
\(x\)が集合\(A\)の要素であることを
$$x \in A$$
と表します。
またその否定の場合、
ポイント
\(y\)が集合\(A\)の要素でない(含まれていない)ことを
$$y \notin A$$
と表します。
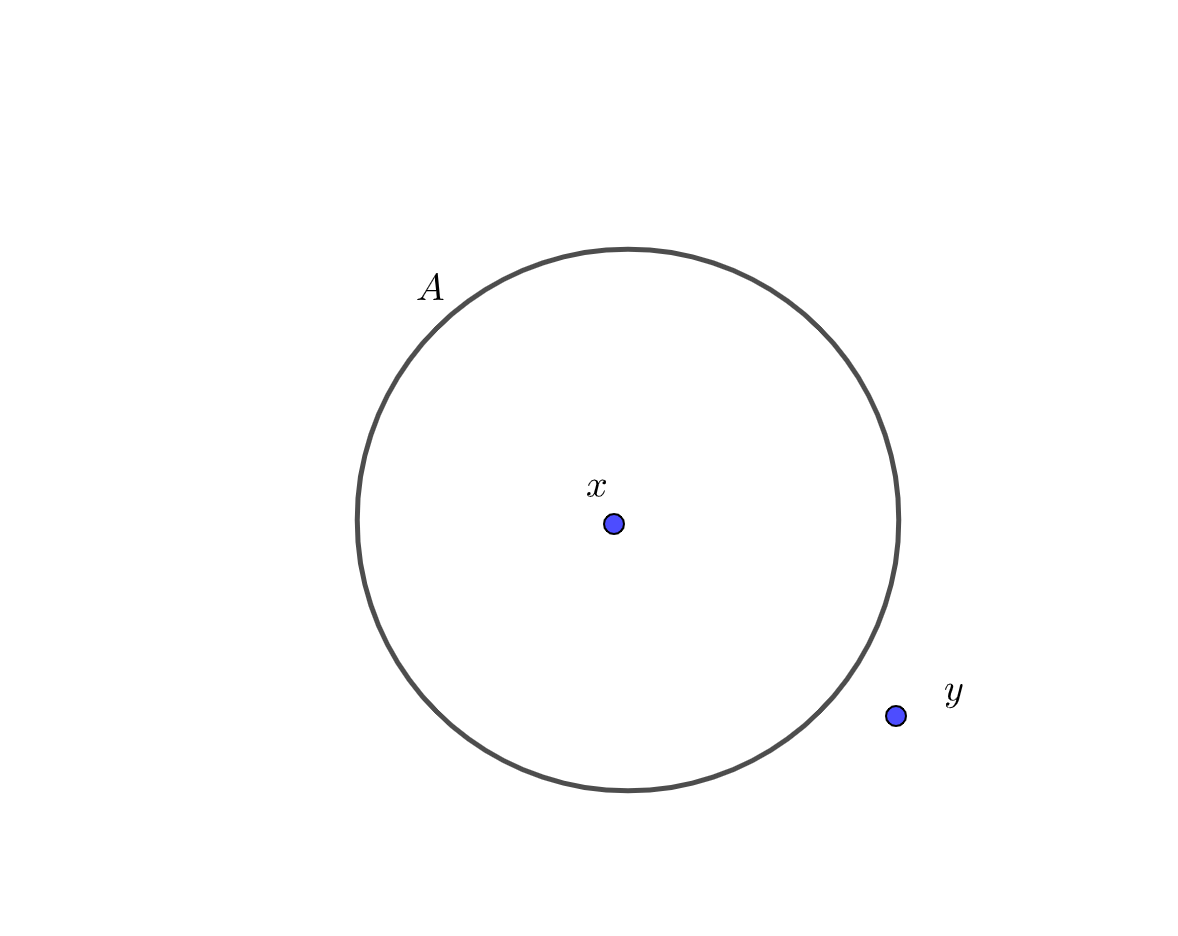
集合の2通りの表し方
一般に、ある集合\(A\)の要素が全て把握できている場合には、
のようにカッコの中に要素を列挙します。
ただ要素を全て書くのはめんどくさいので、境界線ルールがわかっている場合には、
$$A = \left\{ 2n | nは整数 \right\}$$
のように
(※見切れている場合はスクロール)
と書くこともできます。

例題
具体例を見てみましょう。
例題
3の倍数だけを集めて作った集合\(A\)があるとします。
このとき、
$$2, 5, 6, 12, 100$$
のなかで、集合\(A\)の要素となり得るのはどれか。




解答
集合\(A\)は
と表せる。

\(n=2\)のとき、\(3n = 6\)
\(n=4\)のとき、\(3n = 12\)
なので、
またどの整数\(n\)に対しても\(3n \neq 2, 5, 100\)なので、
よって、
より、6、12が集合\(A\)の要素である。
まとめ

まとめ
集合を定義するためには、必ず「この要素は集合に含まれるか」が判別できるようなルールが必要となる。
(含まれるかもしれないし、そうじゃないかもみたいなのはNG)
集合の表し方や、要素との関係自体は難しいものではありません。
しかし、この境界線ルールをもとに「含まれるか否か」の考え方が、実は現代の数学のベースになっています。

今のうちからしっかりと基本を抑えていくようにしましょう!
以上、「集合の表し方と要素について」でした。
チェック問題
例題
ある集合\(A\)の要素は全て7以上16未満の偶数である。このとき集合\(A\)を表せ。
(※見切れている場合はスクロール)

例題
$$B =\left\{ 3k | kは20以下の素数 \right\}$$
と定義される集合\(B\)の要素を全て書き表せ。
20以下の素数は
よってそれぞれ3倍すればOKなので、








