Today's Topic
$$ラジアン=\frac{孤の長さ}{半径}$$




こんなあなたへ
「サインコサインで角度から急に弧度法を使いだしたのはなんで?」
「どうして30度が\(\frac{\pi}{6}\)なの?」
この記事を読むと、この意味がわかる!
- \(\frac{3}{2}\pi = 135^\circ\)
- \(240^\circ = \frac{4}{3}\pi\)

Contents
弧度法(ラジアン)の定義
弧度法の定義は次のようにされます。
定義
円の半径と弧の長さが等しくなるときの中心角を1ラジアン(1[rad])という。
角度というと、分度器で計る\(1^\circ\) や\(180^\circ\)のような度数法がしっくりくる人が多いと思います。
度数法は\(1^\circ\)という単位を基準に、角度の計測を行なっています。
対して弧度法の場合、図のような半径1の円において弧の長さが1となるような角度を1ラジアンといい、この1ラジアンを基準に角度を計量していきます。
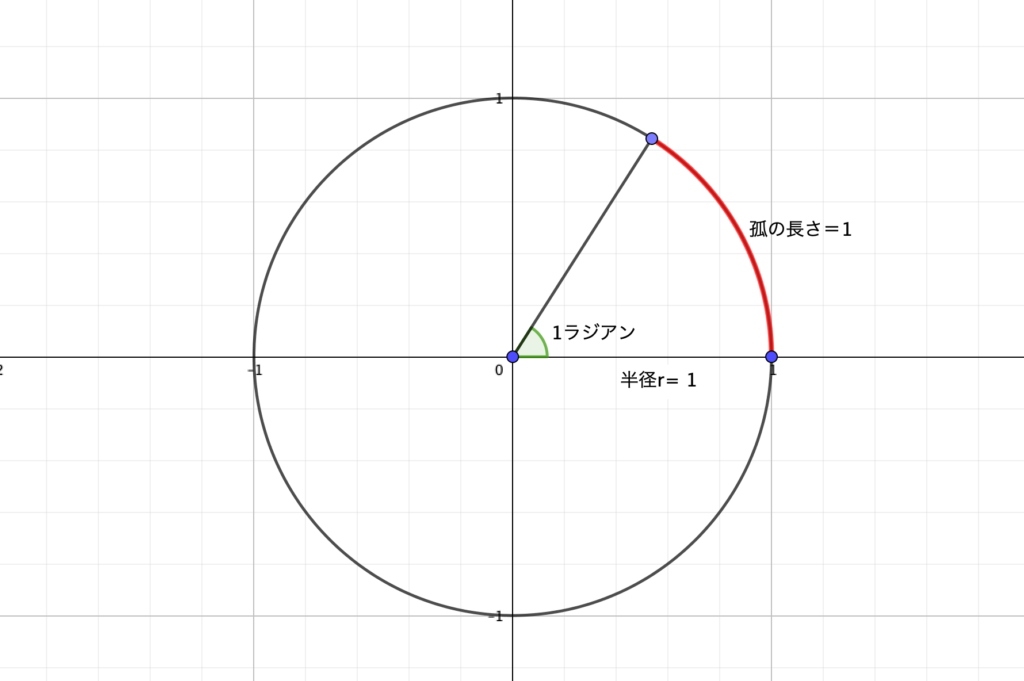

この定義でいくと、半径2の円では孤の長さが2のとき、半径が500のときは孤の長さが500のときが1ラジアンとなります。
つまり
という比例式が得られます。
またこの比例式から、半径1の円では孤の長さが2のとき2ラジアンとなることから、半径1の円では孤の長さが\(x\)のとき中心角は\(x\)ラジアンとなります。
さらに半径\(r\)、中心角\(\alpha^\circ\)の扇型を考えると、孤の長さは通常\(2\pi r\times\frac{\alpha^\circ}{360^\circ}\)で表されるので、
半径が伸びて円が大きくなっても、\(\frac{孤の長さ}{半径}\)を計算すると半径が打ち消しあうため、弧度法も度数法と同じく円の大きさに依存しないことがわかります。
弧度法の性質を考えると変換公式を求めることもできます。

度数法から弧度法(ラジアン)に変換するコツ
変換公式から\(\alpha^\circ=180^\circ\)のとき、ラジアンでは\(\theta=\pi[rad]\)となります。
つまり度数法の\(180^\circ\)を、ラジアンの\(\pi\ [rad]\)と表すということで、度数法から弧度法に変換できるというわけです。
例えば、\(30^\circ\)を弧度法で表現すると、
となります。

ちなみに1ラジアンは何度なのでしょうか。
変換公式を使うと、
となり、約\(57^\circ\)であることがわかります。

弧度法(ラジアン)を使うメリット

確かに言われればそうです。
これまで使い慣れた度数法ではなく、なんでわざわざ新しく定義したラジアンを使わなきゃいけないのでしょうか。
座標系が統一できる
弧度法を使うメリットで一番大きい(と筆者が感じている)ものは、座標系が統一できることです。
例えば\(y=\sin x\)という三角関数を考えてみましょう。
\(x\)が弧度法ではなく度数法を採用している場合でも、\(y=\sin x\)のグラフを描くことはできます。
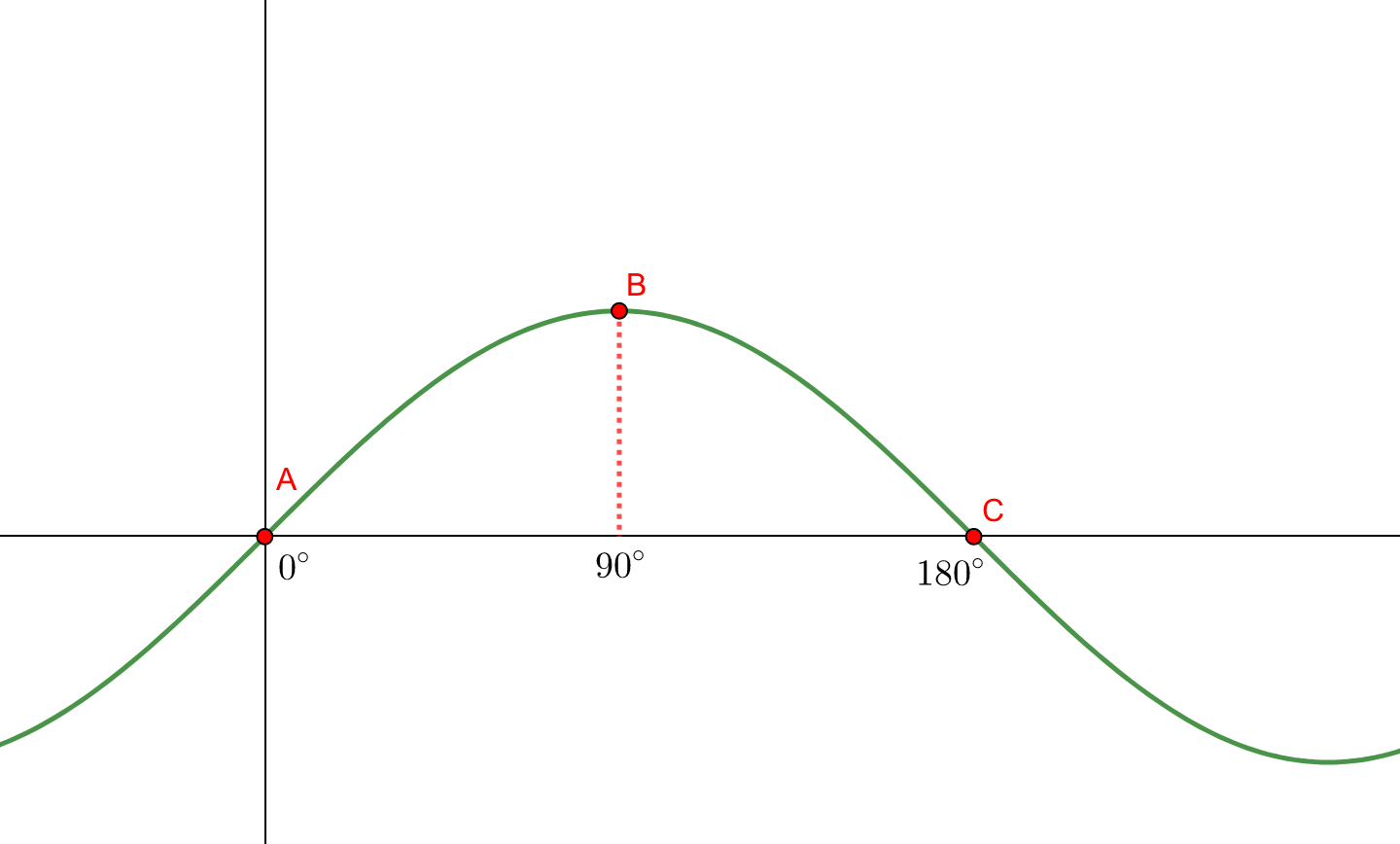

通常使う\(xy\)座標系は\(x\)軸も\(y\)軸も単位がない、もしくは長さを表すものが一般的です。
なので横軸\(x\)の単位が[\(^\circ\)]に限定されていると、他関数のグラフを一緒に考えることができません。
弧度法は性質からも分かる通り、ただの比を表しています。
この記事ではわかりやすいように[rad]表記をしましたが、通常は他の比率と同様、単位を書きません。
単位がない数であることは、座標軸の数値に採用しやすいメリットがあり、数学を発展させる上では弧度法の方が都合が良かったことがわかります。

扇型の面積の表し方が綺麗
中心角\(\alpha^\circ\)の扇型の面積Sの表し方は、
となり、ちょっとぐちゃぐちゃしています。

一方、中心角を\(\theta[rad]\)で表してみると
とかなりコンパクトに表せます。
扇型の面積を求めることはそれほどないですし、他のメリットに比べると大したものではありません。
でもパッと計算できるという点では、メリットと言えますね。
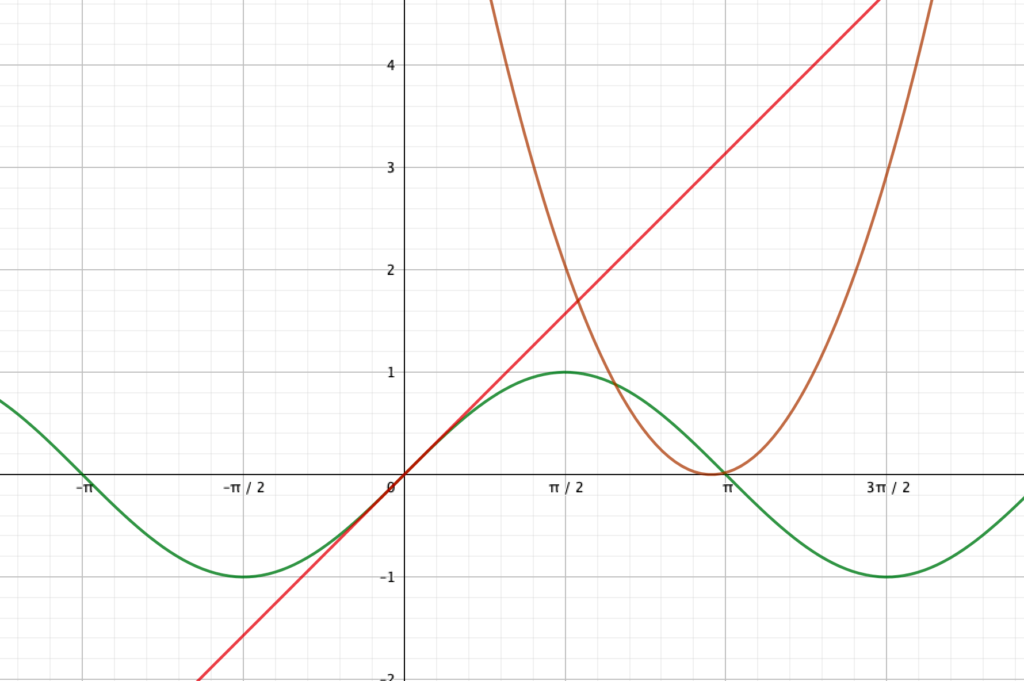
サインコサインの極限や微分、マクローリンが綺麗になる
サインコサインでは、弧度法を採用すると次の3つが成り立ちます。
ここでは意味や証明ではなく、単純に形だけをみてください。
- サインの極限公式:$$\lim_{x\rightarrow 0}\frac{\sin x}{x}=1$$
- サインの微分公式:$$\left(\sin x\right)'=\cos x$$
- サインのマクローリン展開:$$\sin x=x-\frac{x^3}{3!}+\frac{x^5}{5!}-\cdots$$

一方、度数法を採用すると先ほどの3つの公式はこのようになります。
- サインの極限公式:$$\lim_{x\rightarrow 0}\frac{\sin x}{x}=\frac{\pi}{180}$$
- サインの微分公式:$$\left(\sin x\right)'=\frac{\pi}{180}\cos x$$
- サインのマクローリン展開:
$$\sin x=\frac{\pi}{180}x-\frac{\pi^3}{180^3}\frac{x^3}{3!}+\frac{\pi^5}{180^5}\frac{x^5}{5!}-\cdots$$
(※見切れている場合はスクロール)

ただえさえ計算ミスが増えがちなサインコサイン に複雑な係数\(\frac{\pi}{180}\)が加わってしまいました。
マクローリン展開なんてすごいことになっています。
計算を簡単にできるという点だけでも、弧度法を採用するメリットは大いにあります。
度数法と弧度法を場面に応じて切り替える重要性
度数法を使うか、弧度法を使うか。
それは人の好みによると思いますが、この両者にはそれぞれ利点があります。
度数法は具体的に「このくらいの角度だろう」とイメージしやすいですが、計算にはあまり向いていません。
一方で度数法は、計算はかなりしやすくなりますが、イメージは(慣れるまで)しにくいです。

よって、
- 人に伝える必要性があったり、自分で図を意識したい場合には度数法を使う。
- 計算過程では弧度法を使う。
という使い分けがオススメです。
弧度法(ラジアン)のまとめ

まとめ
- $$ラジアン=\frac{孤の長さ}{半径}$$
- 1ラジアンは約\(57^\circ\)
- 度数法から弧度法に変換するときには、\(180^\circ\)を\(\pi\)と表せば良い。
- 弧度法を使うと計算が楽になったり、三角関数を他の関数と一緒に考えることができる。
ラジアンについて、理解は深められたでしょうか?
経験上、文系さんは度数法だけでもいい気がしますが、理系さんはラジアンとこれからずっと付き合っていきます。
その理由はやはり計算が楽になるというメリットや、他グラフと同じ座標系に描けるというメリットがあるから。
結果的には「\(180^\circ\)を\(\pi\)と表せば良かったなぁ」と思いだせればパーフェクトです。
以上、「ラジアンの意味とメリット」でした。
$$\frac{3}{2}\pi = \frac{3}{2}\times 180^\circ = 135^\circ$$
$$240^\circ = \frac{4}{3}\times 180^\circ = \frac{4}{3}\pi$$








