こんなあなたに読んでほしい!
「問題を解いても、なかなか本番で解けるようにならない。」
「公式や解法を暗記しても、点数につながらない。」
という方へ、元文系・3ヶ月で理転できた僕があっという間に数学を得点源にできる考え方をご紹介します。
こんにちは、ラスカルです!
このページを見ているあなたは、これまで必死に勉強してきたはずなのになかなか点数が上がらなくて悩んでいるのだと思います。
勉強してもなかなか解法が思いつかなかったり、点数につながらないととても辛いですよね。
僕が理転したときに学んだのは、数学という分野は効率的に勉強することが非常に重要です。
特に解けない問題に出くわしたときにどう立ち回るか、これが大きな違いを生んでいると思います。
そこで今回は、解けない問題に出会ったときの効率的な立ち回り方をご紹介します。
慣れてくればさらに自分なりにアレンジできると思うので、参考にしていただければ幸いです。
ちなみにこの記事は、以下の言葉に注意して呼んでいただければ読みやすいと思います。
ポイント
- 定義:それが何かを定めた条件。
- 性質:定義を元に発見された条件。
この記事を読むと・・・
- 数学ができる人の勉強法や、考え方を身につけることができる。
- 無駄な暗記をせず、効率的に成績を上げる勉強ができる。
Contents
数学が解けないとき|解答を見て、Whyを確認

数学の問題が解けないとき、多くの場合は『解くための考え方』の知識が不足していることが多いです。
中学校数学で言えば、図形の証明なんかが最たる例。
具体的な場面で解説して見ましょう。
例題
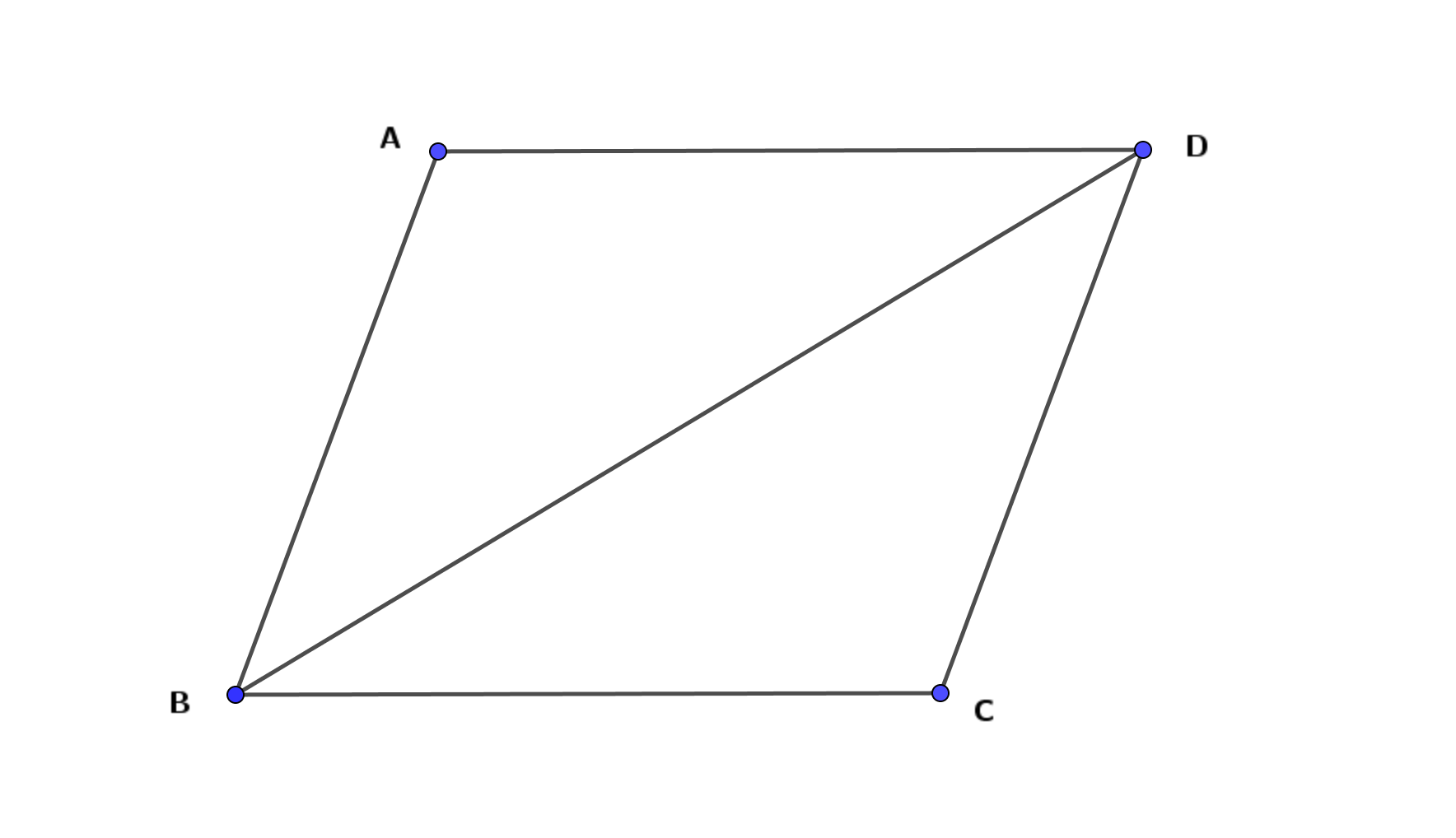
平行四辺形ABCDにおいて、\(\angle A = \angle C\)を証明せよ。
解答
\(\triangle ABD\)と\(\triangle CDB\)において、
平行四辺形の性質より、向かい合う辺の長さが等しいので
$$AB=CD\cdots①$$
平行四辺形の定義より、向かい合う辺が平行なので\(AB\) \\ \(CD\)。
平行な2直線の錯覚は等しいので、
$$\angle ABD = \angle CDB\cdots②$$
共通な辺の長さは等しいので、
$$BD=BD\cdots③$$
①②③より、二組の辺とその間の角がそれぞれ等しいので\(\triangle ABD \equiv \triangle CDB\)。
合同な図形の対応する角は等しいので、
$$\angle A = \angle C$$
以上より平行四辺形ABCDにおいて、
\(\angle A = \angle C\)
この問題の解答におけるポイントは、
という性質を使っている点です。
この性質を使うために、わざわざ\(\triangle ABD \equiv \triangle CDB\)であることを証明しているのです。
このように解答を見ると、
- なぜそのように変形したのか
- なぜそれを証明したのか
など、式変形や証明のWhyが隠されています。
解答を見る大きなメリットは、この部分さえ集中して考えれば問題の解法が自然と理解できるようになる点です。


ただし重要なのは、隠されているということ。
通常数学の解答はここまで親切に書いてくれているものは少なく、自力で変形の意味や証明したことの意味を把握する必要があります。
そして数学が得意な人のほとんどは、この部分に多くの時間を費やしているんですね。
解答を見なければ、このWhyを考えるまでに相当の時間を奪われます。
苦手なうちは全て自分で解くのではなく、まずは解答の意味を把握することから始めましょう。
いろんな問題を解くと、自然といろんな解法に触れることになります。
その解法の中でWhyを徹底的に吸収していくと、次第に問題を解くときに自分で
- 「こんな風に変形したいな」
- 「こんな風に扱いたいな」
という気持ちが芽生えます。
この気持ちが生まれたとき、数学をマスターするまでにはおそらく数日とかからないでしょう。
ポイント
解答の意味を理解するためには、
- なぜそのように変形したのか
- なぜそれを証明したのか
などのWhyを考えよう。
数学が解けないとき|解答や問題を見て、Whatを確認
解法を見ていく中で、変形の意味を考えるWhy以外にも
- この式や言葉はなんなのか
- この性質はなんなのか
を考えることがあります。
これをWhyと対応させて、僕はWhatと呼んでいます。
Whyとの違いは
- Whyは変形の意味や考え方など、その問題を解く上で必要な方法の知識
- Whatは言葉の意味や性質など、その問題を解く上で必要な基本的な知識
と捉えてもらえればいいと思います。
日常場面で例えると、
- Whatの知識が『ノコギリとは何か』
- Whyの知識が『(効率的に切るために)ノコギリは引くときに力を入れればよく切れる』
といった感じです。
このWhatが抜けていると、そもそも解答が読めません。
解答の意味がわからない場合はWhyを突き詰めればいいですが、なんのことを言っているのかわからない場合はWhatを突き詰めましょう。
特に定義や性質がパッと思い浮かばない言葉は注意が必要です。
例えば先ほどの解答で、2つの三角形が合同であることを用いましたがそもそも合同とは何か説明できますか?
- 合同の定義は『2つの図形がぴったり重なること』。
- 2つの図形が合同であるとき、重なっている(対応する)辺や角は等しくる。
- そして2つの図形が合同であるかどうかは、合同条件を確認することで確かめることができる。
このように合同という1つのワードに対して、Whatが持っている意味は膨大な情報量を含んでいます。

ポイント
解答の謎ワードを理解するためには、
- どのような定義か
- どのような性質があるか
を調べれば良い。
数学が解けないとき|【完璧な解答の書き方】考え方が思い浮かぶか確認、逆から書く

Why・Whatに着目して解答の意味を理解できたら、その理解度を試します。
実際に問題を解いてもいいですし、解答を見た問題の解き直しでもいいでしょう。
ここで大事にして欲しいのは、自分の解答が模範解答と全く同じに書けるかではなく、何をすればいいか思いつけるかどうかです。
お手本と同じように書ければいいのは、書写という科目の役割です笑
数学では自分で考え、表現する力が必要です。
- 何をすればいいのか・何を証明すればいいのか
- それを使うためには何をすればいいのか・何を証明すればいいのか
- それを使うためには・・・
を考えて、解答を書くときは考えたことと逆の順番で書けば完璧な解答をかけます。
例えば前述した平行四辺形の証明の問題では、
⒉合同の性質を使うために、\(\triangle ABD \equiv \triangle CDB\)であることを示せばいい。
⒊\(\triangle ABD \equiv \triangle CDB\)を示すために、合同条件を示せばいい。
という考え方が必要です。
解答を見てみると、この逆の順番
⒉合同条件より、\(\triangle ABD \equiv \triangle CDB\)を示す
⒈合同な図形の性質『対応する角がそれぞれ等しい』を使う
となっていますね。
数学が解けないとき|結果を焦らないことが重要
ここまでの話から薄々気がついた人もいるかもしれませんが、暗記よりもよっぽど大変です。
わからないこと(What)を覚えなきゃいけないし、やり方(Why)を理解しなきゃいけないし。
ですが、数学のいい点はこれら1つ1つが独立せずに、繋がっている知識になっているということです。
つまり一回やって終わりではなく、やった回数だけ他の問題が次第に解けるようになるという知識の蓄えが可能なんです。

ただし勘違いしないで欲しいのは、時間がかかるとは言っていません。
時間がどれだけかかるかは、その人のこれまでの勉強量やこれから解く問題量に依存します。
解く問題量を増やし、出会った問題と徹底的に向き合うことで時間はいくらでも短縮できます。
足早に結果だけを求めて暗記に走ったり、自暴自棄にならないようにすれば必ず結果は出ます。
数学が解けないとき|まとめ
まとめ
- 数学の問題を解けるようになるためには、
- いっとき考えて、わからないようであれば積極的に解答を見る。
- 解答を見るときは、Why/Whatを意識して読む。
- もう一度問題を解き、しっかりWhy/Whatが思い浮かぶか確かめる。
- 解答を完璧に仕上げるためにはWhyを意識し、解答は逆の順番で書く。
- 結果は焦らず、着実に取り組むことで必ず出る。
もし数学があなたの得点源でないのなら、それはすごく勿体無いこと。
僕は理転したことで大学の選択肢も、そして就活や人生の選択肢もかなり広がりました。
あなたにとって数学が最高のパートナーになることを願っています。
以上、「数学の問題を完璧に解けるようになる」でした。








