Today's Topic
$$偏差値z=\frac{x-\mu}{\sigma}\times10+50$$
\(x:\)点数、\(\mu:\)平均、\(\sigma:\)標準偏差




こんなあなたへ
「進路指導の時に偏差値で志望校判断されるけど、それって判断基準になってる?」
「進路指導でよく偏差値を生徒に言うけど、意味は知らない」
この記事を読むと・・・
- 偏差値の意味がよくわかる。
- なぜ自分たちを測る指標に、偏差値が採用されているのかがわかる。
さぁ、Let's aim high(高みを目指そう)!!!
偏差値の定義
まず偏差値の定義は、次のようになっています。
偏差値の定義
\(x:\)点数、\(\mu:\)平均、\(\sigma:\)標準偏差とするとき、偏差値\(z\)は
$$z=\frac{x-\mu}{\sigma}\times10+50$$
と定義する。
ではこれからこの式が何を表しているのか、また何を表したくてこのような形になったのかを考えていきます。

偏差値の意味
遼一くんと佑紀乃さんが、2週間前に受けた模試の点数で勝負をします。
二人とも同じ模試の同じ科目を受験して
遼一くん
60点だった。
佑紀乃さん
65点だった。
という場合、より点数の高い佑紀乃さんの方が成績は優秀ということになります。
同じテストであれば、より点数の高い方が優秀ということになります。
しかし模試や入試では、みんながみんな同じテストを同じ条件で受験するとは限りません。
そこで、もし二人が違うテストを受験していて
遼一くん
60点だった。
佑紀乃さん
65点だった。
という場合、どちらが優秀なのでしょうか。
具体的な問題場面
それでは、具体的に次のような問題を考えてみましょう。
例題
遼一くんはA社の、佑紀乃さんはB社の数学模試を受験した。
どちらの模試も平均点が同じ50点だったが、点数の分布が次のようになっていた。
【A社】 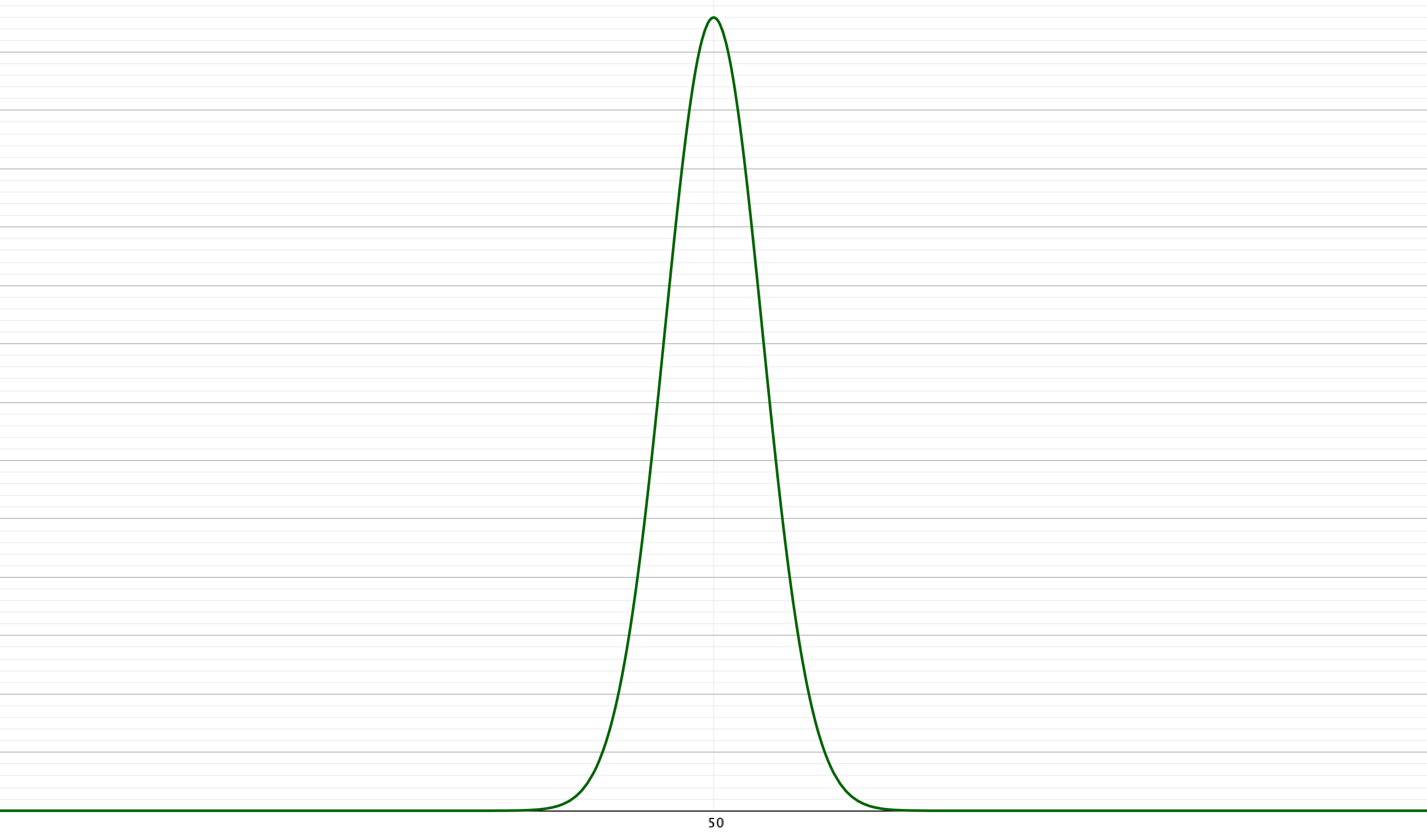
【B社】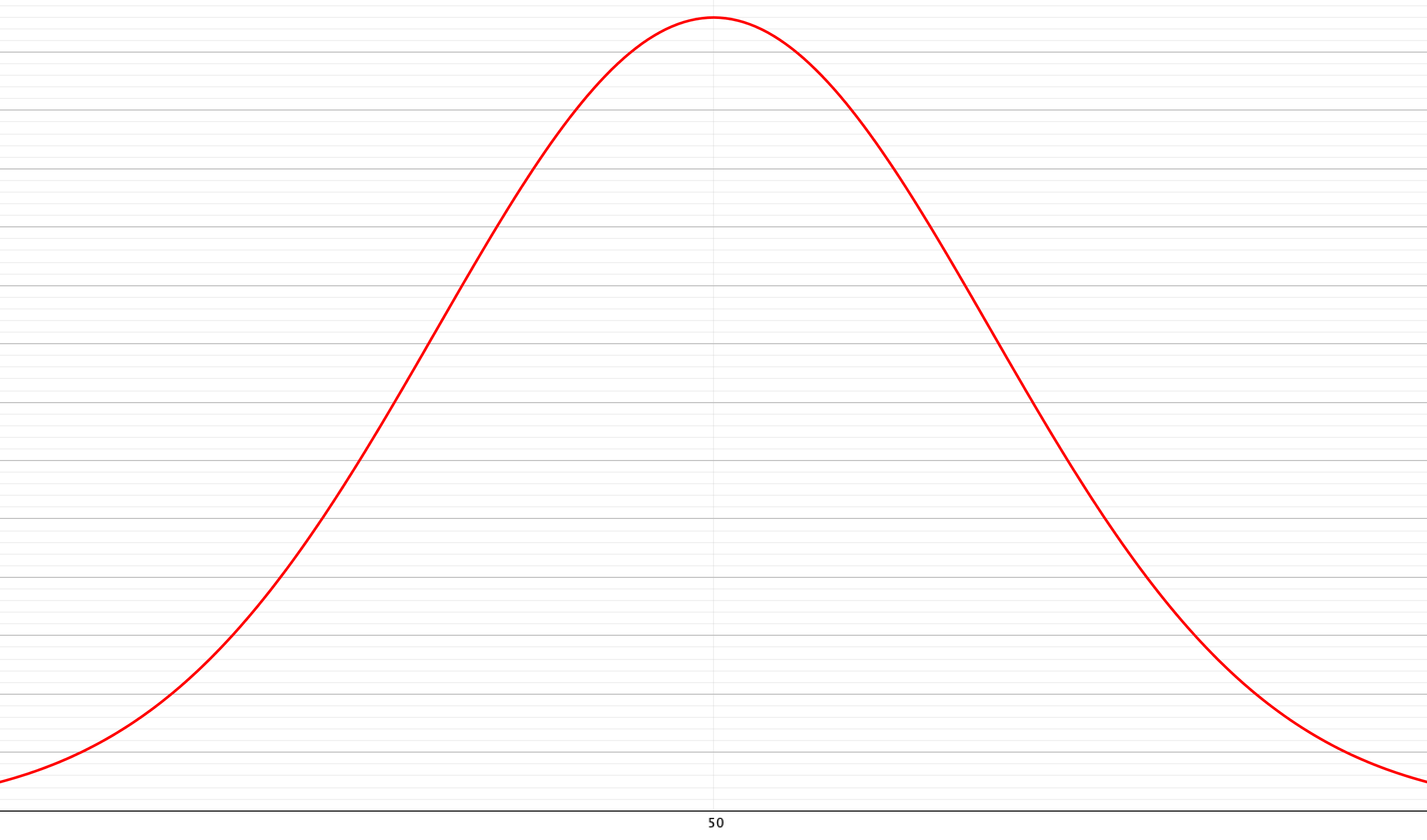
(縦軸:人数、横軸:点数)
このとき、遼一くんと佑紀乃さんの点数を比較すると、どちらの方が優秀と言えるか。

両方の会社の点数分布を見ると、どちらも平均点の人数が最も多くなっています。
ただし、A社の模試は平均点付近に固まっており、高得点を取った人がかなり少ないことから、難易度は高めだったと思われます。
一方、B社の模試はA社と比べると高得点の人も割と多く分布しており、努力がそのまま反映されているようなテストと言えます。
両模試は平均点こそ同じですが、平均点付近に固まっているか、全体的にばらついているかの違いがあります。
当然難易度はA社の方が高かったと思えるので、この感覚を評価基準に組み込みましょう。
【標準偏差の意味】模試の点数分布のばらつきを考えよう。
受験した人の点数について
- ほとんどの人が平均点と同じくらいの点数
- 人によってバラバラ
となっていた場合、前者の方が難しい点数だったと考えられます。

そこで、全体の点数が平均点からどれだけ離れているかを考えると、その模試の難易度がわかりそうです。
まず、\(x\)点とった人が平均\(\mu\)からどれだけ離れているかは、\(x-\mu\)で求めることができますね。これを偏差と言います。
N人全員の偏差を考えることで、各自どれだけ平均から離れているかを考えられます。
すなわち
は、各自の平均点からのズレをまとめて足したものと見なせます。
しかしこのまま足してしまうと、不都合が生じます。
例えば平均30点のテストで28点の生徒と32点の生徒がいたとします。
2人とも2点ずつズレていますが、\((28-30)+(32-30)=-2+2\)となるのでズレの和は0となってしまいます。

そこで、全ての偏差を負の値にならないために2乗します。
(※見切れている場合はスクロール)
さらにこれを人数Nで割ると、
(※見切れている場合はスクロール)
となり、『平均からのズレ』の平均を考えることができます。
ただし勝手に2乗したので
- 単位が点\(^2\)という意味不明なものになっている。
- 値がかなり大きくなる。
というデメリットが発生します。
このデメリットを解消するためにルートをつけてあげます。
(※見切れている場合はスクロール)
これが全体の値のばらつき具合を表す標準偏差と呼ばれるものの定義になります。
このような複雑な式になった理由は、
- 平均点から各自、どれだけ離れているのかを考慮した(偏差)
- 平均からの差が打ち消し合わないように2乗した
- 単位や数量の大きさ問題を解消するためにルートをとった
という作業があったからです。
この流れを理解すると、今後データの活用の問題で楽ができます。
偏差値の定義
$$\sqrt{\frac{\left(x_1-\mu\right)^2+\left(x_2-\mu\right)^2+\cdots+\left(x_N-\mu\right)^2}{N}}$$
偏差値の意味を考える
それでは再び遼一くんと佑紀乃さんの場面に戻ります。
標準偏差は全員分の点数が必要なため、模試を行なった会社しか求めることができません。
そこで標準偏差の開示を求めたところ、
- 【A社】:標準偏差11
- 【B社】:標準偏差21
という結果が得られました。
それではまず遼一くんの偏差値を求めていきましょう。
平均からどれだけ離れた点数を取ったか、は非常に重要な判断材料でした。
そこで偏差
を考えます。
次に点数のばらつき具合について、
- ばらつきが小さいほど、高得点はとりにくかった。
- ばらつきが大きいほど、高得点を取れる人は取っている。
ということが言えるので、ばらつきが小さくなるほど評価するようにしたいですね。
そこで先ほどの偏差の分母に標準偏差\(\sigma\)を置きます。
こうすることでばらつき具合を表す標準偏差が小さくなるほど、値が大きくなる、すなわち優秀さを表すことになります。
実際に計算してみると、遼一くんの場合
となりました。
小数点で扱いにくいので、10倍してわかりやすい数にしましょう。
また、優秀さレベルを表す数値なら0〜100で表した方がわかりやすいです。
そこで0と100の間である50を加えましょう。

同じように佑紀乃さんのも求めると、
(※見切れている場合はスクロール)
となりました。


このように求めたものが偏差値と呼ばれるものです。
異なる教科やテストでも、
- 平均点に着目し、
- 点数のばらつき具合を表す標準偏差に着目し、
- わかりやすいように10倍し50加えた数
である偏差値を比較することで、点数を見比べるよりもより納得のいく評価ができるようになりました。
偏差値の性質
偏差値は平均だけでは測れない、点数のばらつき具合(いわゆるテストの難易度)も考慮した評価値になりましたね。
この偏差値には、面白い性質があります。
それは点数の分布が正規分布と呼ばれる、いわゆる山なりの形になっているときに言えます。
正規分布

この正規分布に似た点数分布のテストであれば、次のようなことが言えます。
- 偏差値が70以上→上位2.2%
- 偏差値が60以上→上位15.8%
- 偏差値が50以上→上位50%
これは点数や平均点、標準偏差にかかわらず成り立ちます。
つまり、偏差値を見れば今回のテストで大体どれくらいの位置にいるのかがわかります。

まとめ
それではまとめです。
まとめ
- 偏差値は異なるテストでも、平均と点数のばらつき具合に着目して、優秀さを比較できるようにした値。
- 偏差値だけをみて、自分が今全体の何%の位置にいるのかがわかる。
偏差値は模試の結果を見るだけでなく、自分のテストを見直す上でも大きな役割を担うことができます。
例えば前回50点だったテストが60点に上がっていたとしても、それはテストが簡単になっただけかもしれません。
偏差値を求めて、前回の偏差値と比較してみれば自分の能力が上がっているかどうかがわかるので、改善点を考える、いい指標にもなります。
偏差値は志望校を決める上で、重要な数値であることに間違いありません。
しかしそれ以前に、過去の自分と比較して何が苦手なのか把握することも忘れないでください。
以上「偏差値の定義」についてでした。








