Today's Topic
方程式\(z^n=\alpha\)の解を複素数\(\alpha\)の\(n\)乗根という。





こんなあなたへ
「\(z^6=1\)の解き方やその意味がわからない。」
「図が出てきたり、解が複数あったりするけどなんで・・・。」
この記事を読むと、この意味がわかる!
- \(z^5=1\)を解け。
- \(z^6=36i\)を解け。

複素数を一気に理解したい方への記事は、こちらにまとめてあります。
複素数のn乗根の解き方|たったの4ステップ
\(n\)乗根は解き方はそれほど難しくなく、本質に価値があるのでチャチャッとやっつけちゃいましょう。
ポイント
\(z^n=\alpha\)の解を求めるためには、
- \(z\)も\(\alpha\)も極形式にする。
- \(z^n\)をドモアブる。
- 2.と\(\alpha\)を比較する。
- \(\theta\)を考える。
のようにすれば良い。
ド・モアブルの定理について復習したい人はこちらを参考にしてください。
続きを見る



ド・モアブルの定理の証明と問題場面→極形式の形に直せればOK
それでは具体例を通して、複素数の\(n\)乗根を考えてみましょう。
例題
方程式\(z^6=1\)を解け。
step
1\(z\)も1も極形式にする。
複素数\(z\)を2つの実数\(r,\theta\)を用いて
とする。
続いて実数1を複素数とみなすと、\(1=1+0i\)となることから
と表せる。
step
2\(z^6\)をドモアブる。
\(z^6\)にドモアブルの定理を適用します。
Step1より、\(z=r\left(\cos\theta+i\sin\theta\right)\)なので、
となります。
step
3比較する。
最後に\(z^6\)と1を比較していきます。\(z^6=1\)より、
これにより\(r=1\)とわかります。
問題は\(\theta\)です。
step
4\(\theta\)を求める。
パッと見、\(6\theta=0\)となりそうですが、これは不十分です。
\(\cos0\)と\(\sin0\)の値と一致する値は0の他にも、
と複数の答えがあります。


\(\cos2\pi=1,\sin2\pi=0\)
も答えだし、
\(\cos (-2\pi)=1,\sin(-2\pi)=0\)
も答えになるにゃ。
つまり\(\pm 2n\pi\)(\(n\)は整数)が付け加わればその分だけ、 すべて答えになるということです。
よって
が正しい答えになります。
よって、
\(\theta=\frac{1}{3}n\pi\)
が得られます。
\(z\)を極形式にした際、\(\theta\)の範囲を\(0≦\theta<2\pi\)と制限していました。
これにより、\(0≦\frac{1}{3}n\pi<2\pi\)となり、これを満たす\(n\)は
\(n=0,1,2,\cdots ,5\)
の6通りとなります。


最後はそれぞれの解、\(z\)の値を求めて終わりです。
\(z=\cos\frac{0\pi}{3}+i\sin\frac{0\pi}{3} =1\)
\(n=1\)のとき、
\(z=\cos\frac{\pi}{3}+i\sin\frac{\pi}{3} =\frac{1}{2}+\frac{\sqrt{3}}{2}i\)
\(n=2\)のとき、
\(z=\cos\frac{2\pi}{3}+i\sin\frac{2\pi}{3} =-\frac{1}{2}+\frac{\sqrt{3}}{2}i\)
\(n=3\)のとき、
\(z=\cos\frac{3\pi}{3}+i\sin\frac{3\pi}{3} =-1\)
\(n=4\)のとき、
\(z=\cos\frac{4\pi}{3}+i\sin\frac{4\pi}{3} =-\frac{1}{2}-\frac{\sqrt{3}}{2}i\)
\(n=5\)のとき、
\(z=\cos\frac{5\pi}{3}+i\sin\frac{5\pi}{3} =\frac{1}{2}-\frac{\sqrt{3}}{2}i\)
(※見切れている場合はスクロール)
よって、
となります。
\(n\)乗根の周期性
ここでは\(z^6=1\)を求める際、\(0≦\theta<2\pi\)と制限していました。
この制限を外して考えてみるとどうなるでしょうか。
当然\(0≦\frac{1}{3}n\pi<2\pi\)という制限も外れるため、無数の\(n\)の値が定まります。
では\(n=6\)のときを考えてみましょう。
となります。
これは\(n=1\)のときと解が同じですね。
このように制限を外しても、結局新しい解は生まれず、ずーっと同じ解をぐるぐる巡回するだけなのです。
円一周分\(0≦\theta<2\pi\)と制限すれば、すべての複素数解は出揃います。
それ以降考えても同じ解が巡回するだけなので、このように制限するわけです。


複素数のn乗根の図的な意味
得られた複素数解を複素平面上にプロットすると、半径1の円周をちょうど6等分する場所に位置していることがわかります。
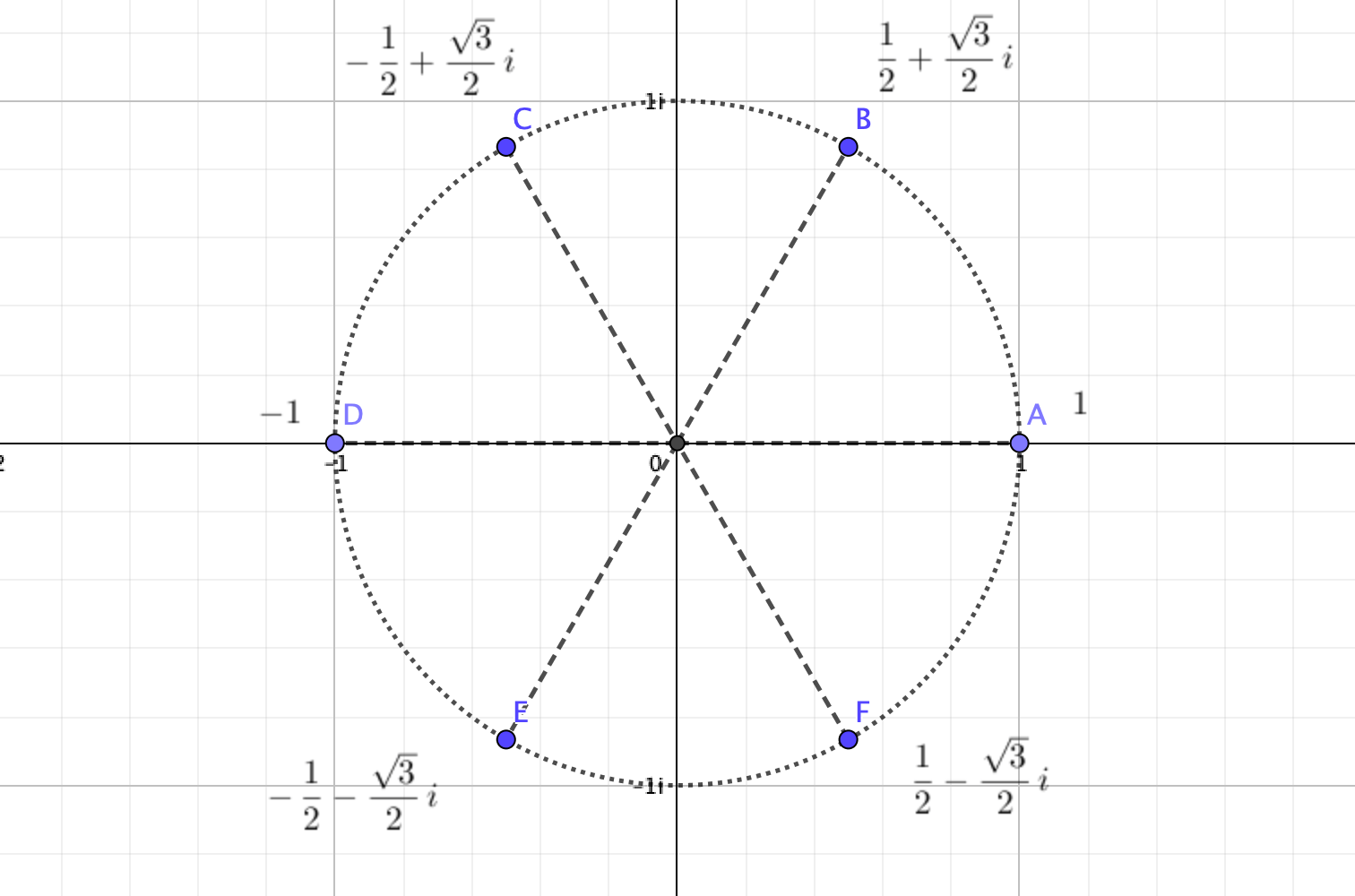

このように
ポイント
\(z^n=\alpha\)を満たす複素数の\(n\)乗根は、半径\(r\)の円周を\(n\)等分する
ことがわかります。


複素数のn乗根と実数のn乗根の比較
複素数の理解を深めるために、実数の\(n\)乗根も考えてみましょう。
これまで実数範囲で1の6乗根を考えろ、と言われると\(\pm\sqrt[6]{1}=\pm1\)の解のみしか考えられませんでした。
他にも2の3乗根なども\(\sqrt[3]{2}\)と、1つや2つの解しか求められませんでした。
ところが解の範囲を複素数まで広げると、1の6乗根には
と6つも解があることがわかりました。
2の3乗根は
(※見切れている場合はスクロール)
と3つの解があることがわかります。
一般的に解を複素数まで拡張すると、\(n\)次方程式は\(n\)個の解を持つことがわかります。
これを代数学の基本定理と言います。
\(n\)次方程式について、実数世界では解がいくつ存在するのかわかりませんが、複素数の世界では\(n\)個と断言できるようになるわけです。
まとめ


まとめ
\(z^n=\alpha\)の解を求めるためには、
- \(z\)も\(\alpha\)も極形式にする。
- \(z^n\)をドモアブる。
- 2.と\(\alpha\)を比較する。
- \(\theta\)を考える。
のようにすれば良い。
n乗根は複素平面上の円を、n等分するように分布する。
n乗根の解を複素数まで拡張することで、n次方程式にはn個の解があることが言える(代数学の基本定理)。
このように、n乗根はドモアブルを使って解決することができ、それによって代数学の基本定理という最強の武器を手に入れることになります。
計算もイメージもそれほど難しくないので、数問解いて慣れておくようにしておいてください。
以上、「複素数のn乗根について」でした。
Q. \(z^5=1\)を解け。
\(z=r\left(\cos\theta+i\sin\theta\right)\ (0≦\theta<2\pi)\)とおくと、
$$r^5\left(\cos 5\theta + i \sin 5\theta\right)=\left(\cos0+i\sin0\right)$$
よって\(r=1,\theta=\frac{0+2n\pi}{5}\ (n=0,1,2,3,4)\)。
以上より、解は以下5通り。
(※見切れている場合はスクロール)
Q.\(z^6=36i\)を解け。
\(z=r\left(\cos\theta+i\sin\theta\right)\ (0≦\theta<2\pi)\)とおくと、
\(36i=6\left(\cos\frac{\pi}{2}+i\sin\frac{\pi}{2}\right)\)より、
$$r^6 \left( \cos 6\theta + i \sin 6\theta \right)=6 \left( \cos \frac{\pi}{2}+i \sin \frac{\pi}{2} \right)$$
よって\(r=\sqrt[6]{6},\theta=\frac{\pi}{2}+2n\pi=\frac{1+4n}{12}\pi\ (n=0,1,2,3,4,5)\)。
以上より、解は以下6通り。
$$z=\sqrt[6]{6}\left(\cos\frac{5\pi}{12}+i\sin\frac{5\pi}{12}\right)$$
$$z=\sqrt[6]{6}\left(\cos\frac{9\pi}{12}+i\sin\frac{9\pi}{12}\right)=-frac{sqrt[6]{6}}{sqrt{2}}+frac{sqrt[6]{6}}{sqrt{2}}i$$
$$z=\sqrt[6]{6}\left(\cos\frac{13\pi}{12}+i\sin\frac{13\pi}{12}\right)$$
$$z=\sqrt[6]{6}\left(\cos\frac{17\pi}{12}+i\sin\frac{17\pi}{12}\right)$$
$$z=\sqrt[6]{6}\left(\cos\frac{21\pi}{12}+i\sin\frac{21\pi}{12}\right)=frac{sqrt[6]{6}}{sqrt{2}}-frac{sqrt[6]{6}}{sqrt{2}}i$$
(※見切れている場合はスクロール)









