Today's Topic
$$\overrightarrow{a}\cdot\overrightarrow{b}=|\overrightarrow{a}||\overrightarrow{b}|\cos \theta$$
$$|a|^2=\overrightarrow{a}\cdot\overrightarrow{a}$$




こんなあなたへ
「内積がなにを意味しているのか知りたい」
「内積っていつ使うの?」
この記事を読むと、この意味がわかる!
- 内積の意味するもの
- 内積の重要公式・つかうポイント
Contents
内積の公式
ベクトルの内積は、2つのベクトルから生成するもので、
ポイント
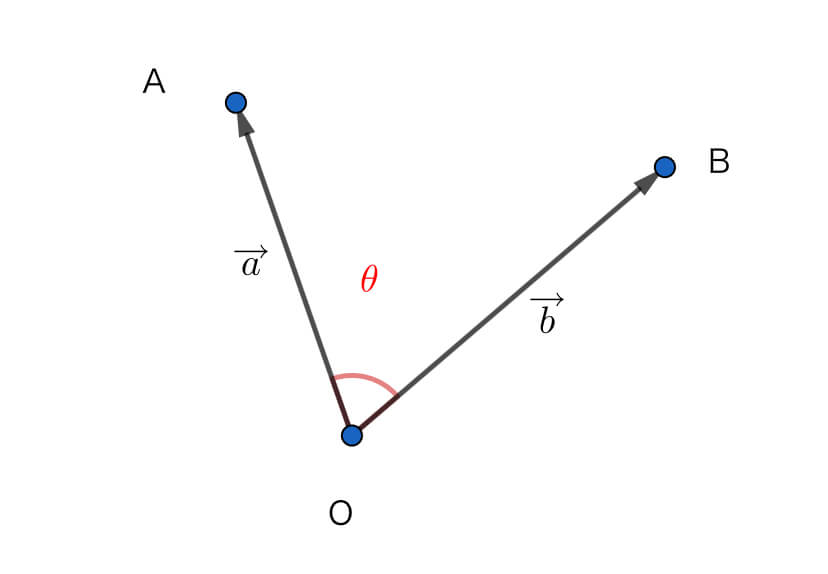
図のような2つのベクトル\(\overrightarrow{a},\ \overrightarrow{b}\)の内積は
$$\overrightarrow{a}\cdot\overrightarrow{b}=|\overrightarrow{a}||\overrightarrow{b}|\cos \theta$$
で求める。
とされています。

また、ベクトルの内積を成分表示で考えると、次のようなことがわかります。
ポイント
2つのベクトル
$$\overrightarrow{a}=\begin{pmatrix}a_x\\ a_y\\ \end{pmatrix}$$
$$\overrightarrow{b}=\begin{pmatrix}b_x\\ b_y\\ \end{pmatrix}$$
の内積は
$$\overrightarrow{a}\cdot\overrightarrow{b}=a_x b_x + a_y b_y$$
で求める。



ここから先は、内積の正体について考えていきましょう。
内積の意味→力のした仕事
内積を計算すること自体はそれほど難しいことではないのですが、内積がなにを表しているのか理解している人はそれほど多くいません。
結論から述べると、内積は『力のした仕事』のことを表しています。


下の図のように、ある物体を力\(F[N]\)で、力を加えた方向に\(x[m]\)だけ引っ張ってみます。
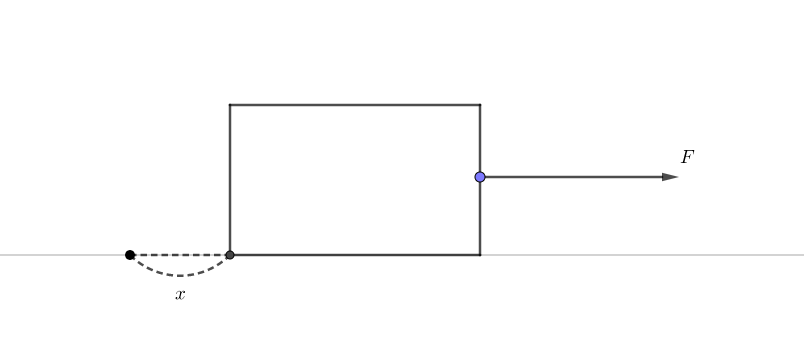
このとき物体を動かす力Fは
だけ仕事をしています。
ここで大事なのが、物体を動かす力の向きと物体の移動する向きは、共に同じ向きでなければなりません。
つまり向きも考慮して正確にいうのであれば、下の図のようにベクトルで表記する方が正しいです。
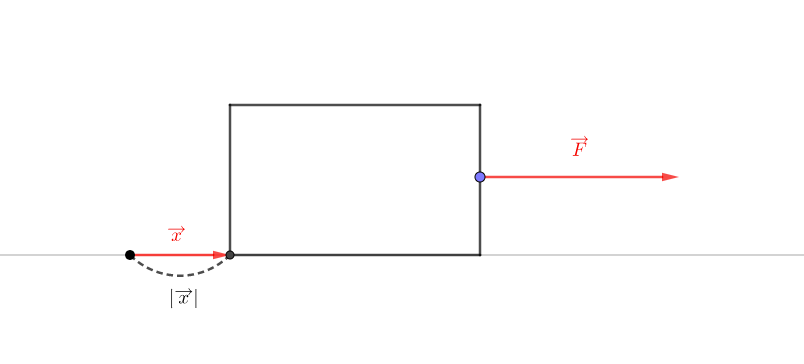
このとき力\(F\)のした仕事は、
と表せます。

では、力の向きと移動する向きが異なっている場合はどうすればいいのでしょうか。
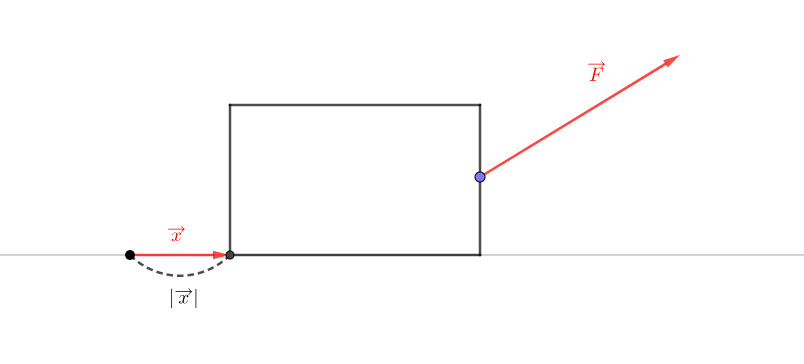
答えは簡単で、そろえてあげればいいのです。
力\(F\)の向きを\(\overrightarrow{x}\)と同じ、水平方向にしてみましょう。
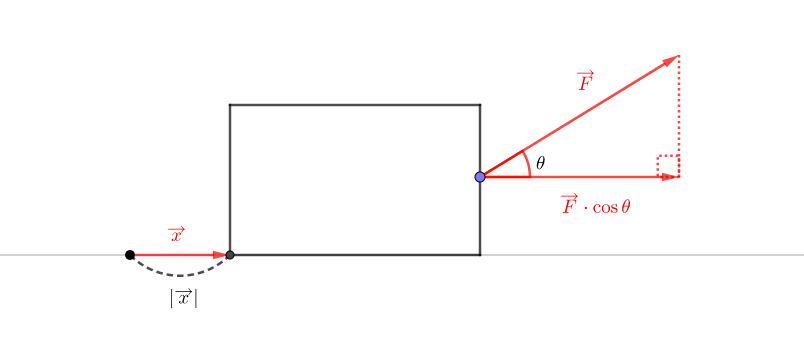
このとき斜辺が\(| \overrightarrow{F} |\)の直角三角形を考えると、\(\overrightarrow{F}\)が水平面から\(\theta\)だけ傾いているとき、水平方向に加わる力は
と表せます。
よってこのとき力\(\overrightarrow{F}\)がした仕事は、
となります。
順番を入れ替える(積の交換法則を使う)ことで、
となるので、力\(F\)のした仕事\(W\)が内積を表していることがわかります。


内積を使うポイント→実数・角度・垂直・ベクトルの大きさ

数学の世界のベクトルでは、内積の意味は全く重視されず、ベクトルを扱うための手法として内積が用いられます。
内積を用いることで得られるメリットは、主に次の3つ。
内積がくれるメリット①:扱いにくいベクトルから、扱いやすい実数に変換
ベクトルは、平行移動を表す数量として考えられました。
ベクトルの意味について復習したい人はこちらを参考にしてください。
続きを見る

ベクトルってナニ?考える意味と、基本的な公式一覧→図形を扱いやすくするツールです。
実数などの数とは違い、向きを持つ特殊な数です。そのため
$$3+\overrightarrow{x}$$
のような計算は、あまり意味を持ちません。


つまり計算するとなると、ベクトル表記は正直めんどくさいわけです。
ここで内積の公式をもう一度見てみると、
と、右辺が実数になっていることがわかります。
これによって、ベクトルを『計算する』という(数学では当たり前の)処理をしやすくなります。


内積がくれるメリット②:成分が分かっていれば、なす角がわかる
2つのベクトルの成分が分かっている場合、内積は
と表すことができました。
成分が分かっている場合、ベクトルの大きさ\(|\overrightarrow{a}|,|\overrightarrow{b}|\)は、
$$|\overrightarrow{b}|=\sqrt{{b_x}^2+{b_y}^2}$$
で求めることができましたので、内積を
(※見切れている場合はスクロール)
と表すこともできます。
よって、
(※見切れている場合はスクロール)
が成り立つため、整理すると、
と、コサインの値を求めることができました。


2つのベクトルの位置関係がいまいちわかっていないのに、コサインの値、つまりは角度が求められるようになりました。


内積がくれるメリット③:垂直条件があるとき、数学の神条件「=0」が使える
2つのベクトルが垂直に交差するとき、2つのベクトルがなす角は\(90^{\circ}\)になります。

よって、内積は
となります。
つまり内積が0であれば、2つのなす角は\(90^{\circ}\)とわかりますね。
また、『=0』は、数学の中でもかなり有効な、そして強力な条件です。
図が示され、2つのベクトルのなす角が\(90^{\circ}\)になっている場合は、積極的に活用しましょう。
内積がくれるメリット④:どんなベクトルの大きさも求められる
2つのベクトルが、互いに同じである\(\overrightarrow{a}\)であるとした時、2つのベクトルの内積は
(※見切れている場合はスクロール)
と表せます。
この式は逆から考えると、かなり有効です。
この式は、ベクトルの大きさを2乗すると内積に分解できることを表しています。


例題
$$|\overrightarrow{a}|=3,\ |\overrightarrow{b}|=2,\ \overrightarrow{a}\cdot\overrightarrow{b}=-1$$
を満たす時、以下の値を求めよ。
$$|\overrightarrow{a}+3\overrightarrow{b}|$$
ベクトルの大きさは、黙って2乗して内積分解すべし!
解答
(※見切れている場合はスクロール)
注意
ベクトルの内積も分配法則・交換法則が成り立つため、
$$|\overrightarrow{a}+3\overrightarrow{b}|^2 = \overrightarrow{a}\cdot\overrightarrow{a}+6\overrightarrow{a}\cdot\overrightarrow{b}+9\overrightarrow{b}\cdot\overrightarrow{b}$$
$$(a+3b)^2=a^2+6ab+9b^2$$
(※見切れている場合はスクロール)
と、\(|\overrightarrow{a}+3\overrightarrow{b}|^2\)と\((a+3b)^2\)は、ほぼ同じ計算結果になります。
に注意すると、
(※見切れている場合はスクロール)
となるので、




内積まとめ:ベクトルの式変形の定番


まとめ
ベクトルの内積は、物体を動かす仕事を表す。
ベクトルの内積は、
- ベクトルを実数化できる
- 2つのベクトルのなす角がわかる
- 垂直条件の時、内積から最強の条件が手に入る
- $$|a|^2=\overrightarrow{a}\cdot\overrightarrow{a}$$
のメリットがある。
ベクトルの内積は、本来の意味から離れてベクトル計算に大きな意味を与えます。
内積で重要な公式は、
$$\overrightarrow{a}\cdot\overrightarrow{b}=a_x b_x + a_y b_y$$
$$|a|^2=\overrightarrow{a}\cdot\overrightarrow{a}$$
の3つだけ。


ベクトルの問題を解く上では必須の計算ツールになるので、ぜひいくつか練習問題をといて、さっさとマスターしてあげてください。
以上、「内積の本質と重要公式について」でした。








