ベクトルってナニ？考える意味と、基本的な公式一覧→図形を扱いやすくするツールです。

Today's Topic

$$\overrightarrow{OB}=\overrightarrow{OA}+\overrightarrow{AB}$$

小春

楓くん、今日はねベクトルを教えて欲しいの！

いいけど、急にどうしたの？

楓

小春

ベクトルって、定義の言っていることは分かんなくはないんだけど、意味があまりパッとしなくて。

なるほど、ベクトルは確かに意味がわかりにくいかもね。

楓

小春

だから今日は、ベクトルの意味と使いかたを教えて！

こんなあなたへ

「ベクトルの言っていることがわからない、何したいの？」

「ベクトルを使う場面がはっきりしない、必要なの？」

この記事を読むと、この意味がわかる！

ベクトルの意味と基礎
ベクトルの使い方

Contents

1 ベクトルの意味｜平行移動を考えている
2 ベクトルの成分表示｜横にいくつ、縦にいくつ動いたか
- 2.1 等しいベクトルとは？｜同じ「平行移動」を表す
3 ベクトルの大きさ｜三平方の定理を考えている
4 ベクトルの種類｜「向き」「移動距離」「場所」に着目
5 ベクトルを考えるメリット｜図形を数式に落とし込む
- 5.1 実践的なベクトルの例題
6 ベクトルのまとめ

ベクトルの意味｜平行移動を考えている

楓

ベクトルは「平行移動を可視化したもの」と捉えると、考えやすくなるよ！

具体的な場面で考えてみましょう。

座標平面上に３つの点、

$$O(0,0),\ A(3,1),\ B(4,5)$$

を考えてみます。

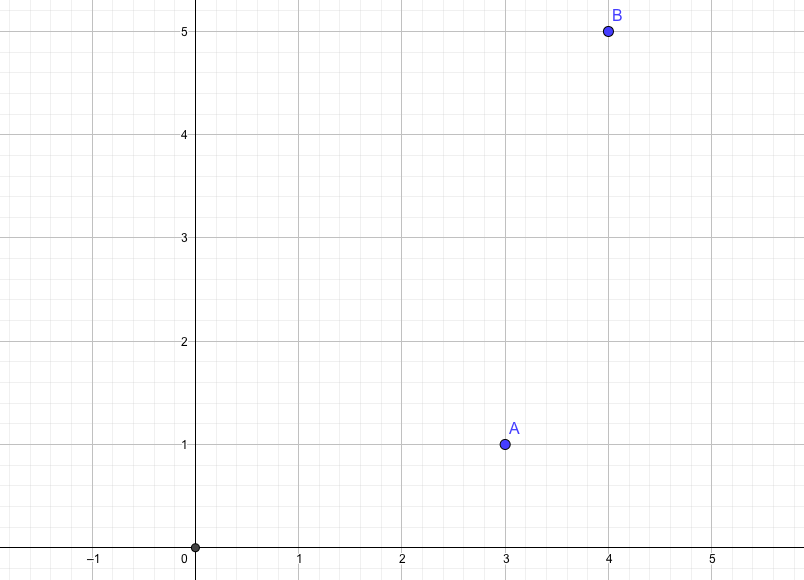
点Oを横に＋3、縦に＋1平行移動させると、点Aと一致します。この移動を$\overrightarrow{OA}$と表します。

同様に、点Aを横に＋1、縦に＋4平行移動させると点Bと一致し、この移動を$\overrightarrow{AB}$と表します。

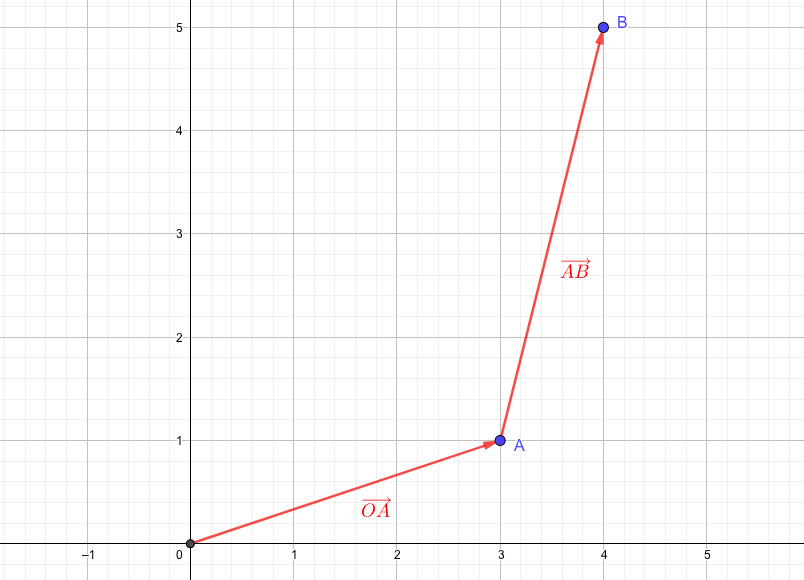
ではここで、点Oから点Bに移動する方法について考えてみましょう。

小春

え？点Oを横に＋4、縦に＋5平行移動すればいいんじゃないの？

点Oを点Aの位置に平行移動させて、そこから点Bに移動させる方法もあるよ。

楓

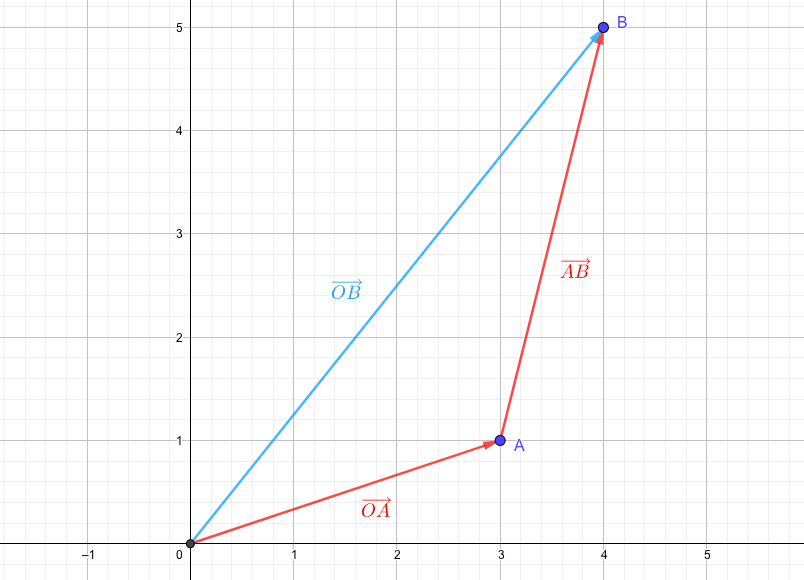
点Oから直接、点Bに移動する場合、この移動は$\overrightarrow{OB}$と表すことができます。

一方で点Oから点Aに移動させて、点Aから点Bに移動させるような、点Aを経由する移動を$\overrightarrow{OA}+\overrightarrow{AB}$と表すことにすると、

$$\underbrace{\overrightarrow{OB}}_{直接移動}=\underbrace{\overrightarrow{OA}+\overrightarrow{AB}}_{点Aを経由した移動}$$

と表すことができます。

楓

どちらも同じ移動を表していることには変わりないからね。

ベクトルの成分表示｜横にいくつ、縦にいくつ動いたか

ここまでは、点Oから点Aへの平行移動を$\overrightarrow{OA}$として、視覚的に捉えてきました。

でも結局、どんな平行移動をしたのか説明するには

横（$x$軸方向）にいくつ進み、縦（$y$軸方向）にいくつ進んだか

を話してあげればいいですよね。

原点Oから点Aに平行移動した際、

$x$軸方向に＋3、$y$軸方向に＋1だけ動いているので、$\overrightarrow{OA}$を次のように表してみます。

$$\overrightarrow{OA}=\begin{pmatrix}3 \\1 \\ \end{pmatrix}$$

このように点Oを、$x$軸方向に$+p$、$y$軸方向に$+q$だけ平行移動させて点Xに移動させたとき

$$\overrightarrow{OX}=\begin{pmatrix}p \\q \\ \end{pmatrix}$$

と表す方法をベクトルの成分表示と言います。

楓

教科書では、スペースの関係上、$\overrightarrow{OX}=(p,q)$と表すことが多いけれど、座標と混同するから縦表記の方がオススメ

座標は位置を表していて、ベクトルは平行移動を表す。全く別の考え方だもんね。

小春

先ほどの図をもう一度見てみましょう。

座標に着目してみると、

点Aから点Bに移動するためには、$x$軸方向に$+1$、$y$軸方向に$+4$だけ
点Oから点Bに移動するためには、$x$軸方向に$+4$、$y$軸方向に$+5$だけ

平行移動していることがわかります。

よって、$\overrightarrow{AB},\ \overrightarrow{OB}$は次のように成分表示できます。

$$\overrightarrow{AB}=\begin{pmatrix}1 \\4 \\ \end{pmatrix}$$
$$\overrightarrow{OB}=\begin{pmatrix}4 \\5 \\ \end{pmatrix}$$

成分表示の場合、２つのベクトルの和は$x,y$それぞれの成分の和で表すことができます。

$$\begin{align} \overrightarrow{OA}+\overrightarrow{AB} &=\begin{pmatrix}3 \\1 \\ \end{pmatrix} + \begin{pmatrix}1 \\4 \\ \end{pmatrix}\\\ &= \begin{pmatrix}3+1 \\1+4 \\ \end{pmatrix}\\\ &= \begin{pmatrix}4 \\5 \\ \end{pmatrix}\\\ \end{align}$$

$\overrightarrow{OB}=\begin{pmatrix}4 \\5 \\ \end{pmatrix}$と、$\overrightarrow{OA}+\overrightarrow{AB}=\begin{pmatrix}4 \\5 \\ \end{pmatrix}$であることからも、

$$\overrightarrow{OB}＝\overrightarrow{OA}+\overrightarrow{AB}$$

が成り立ちますね。

また移項しただけですが

$$\overrightarrow{AB}＝\overrightarrow{OB}+\overrightarrow{OA}$$

というように分離もできます。よく問題で使う変形なので、合わせて覚えておきましょう。

等しいベクトルとは？｜同じ「平行移動」を表す

ここでちょこっと補足です。

ベクトルはあくまで、平行移動を表すものであり、どの点を移動させたかは重要ではありません。

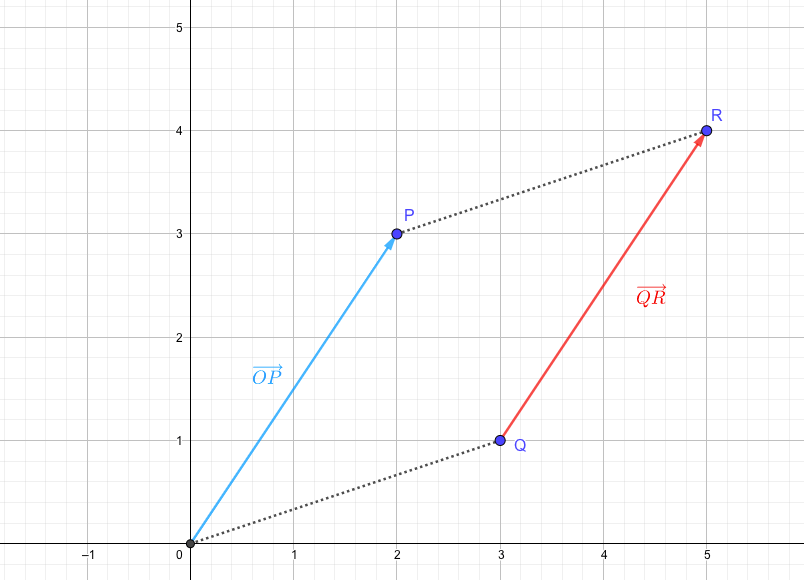
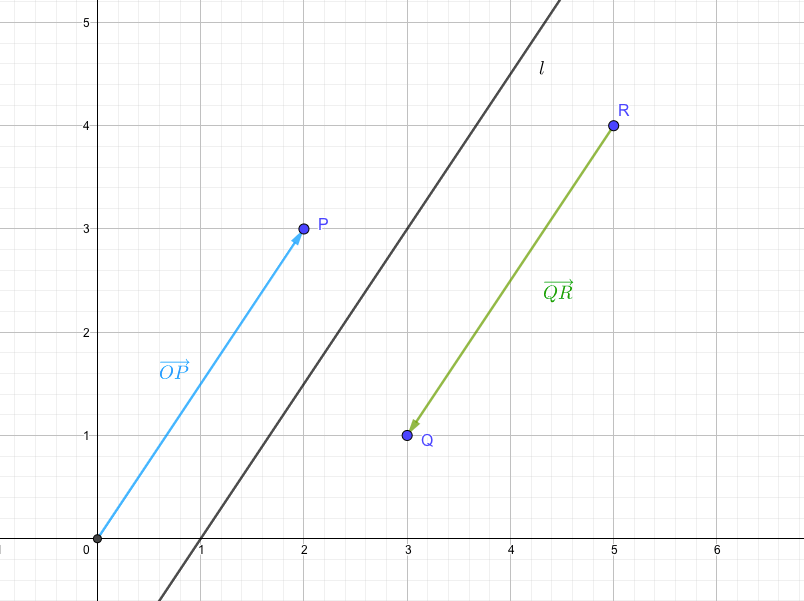
例えば、次の図を見てください。

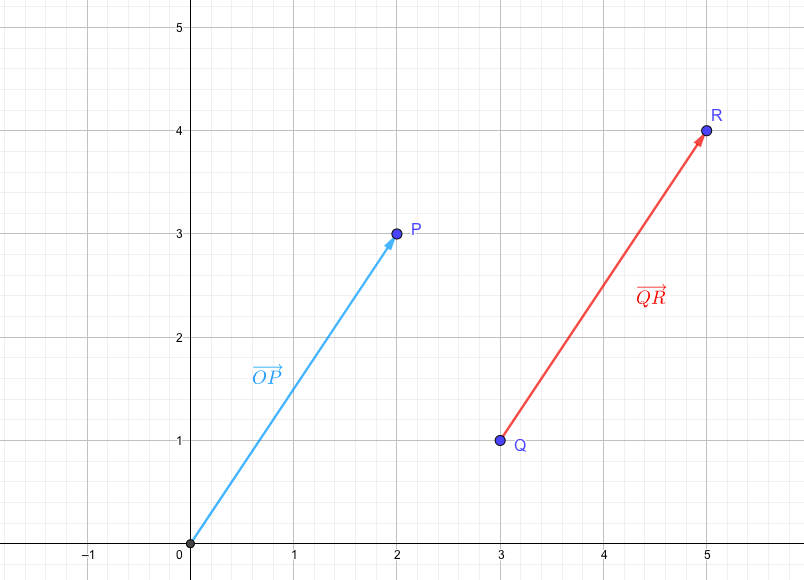
$\overrightarrow{OP}$は点Oから点Pへの平行移動を表す。
$\overrightarrow{QR}$は点Qから点Rへの平行移動を表す。

ということから、別物のベクトルと見えますが、どちらも$x$軸方向に$+2$、$y$軸方向に$+3$の平行移動を表しています。

つまり同じ平行移動を表しているので、

$$\overrightarrow{OP}=\overrightarrow{QR}\left(=\begin{pmatrix}2\\3\\ \end{pmatrix}\right)$$

が成り立ちます。

楓

あくまでベクトルは、移動に着目した数量だということ！

２つの等しいベクトルは、成分が同じになるのね。

小春

もちろん平行移動なので、２つの等しいベクトルには平行な関係があります。

ベクトルの大きさ｜三平方の定理を考えている

小春

ベクトルは平行移動なのに、「大きさ」ってなんかへんな感じ。。。

ベクトルの大きさは、「移動距離」を表すよ！

楓

ベクトルはこれまで、「横にいくつ、縦にいくつ」移動したかを表す数量として扱いました。

これに対してベクトルの大きさとは、始点から終点までの長さ、いわゆる最短距離のことを言います。

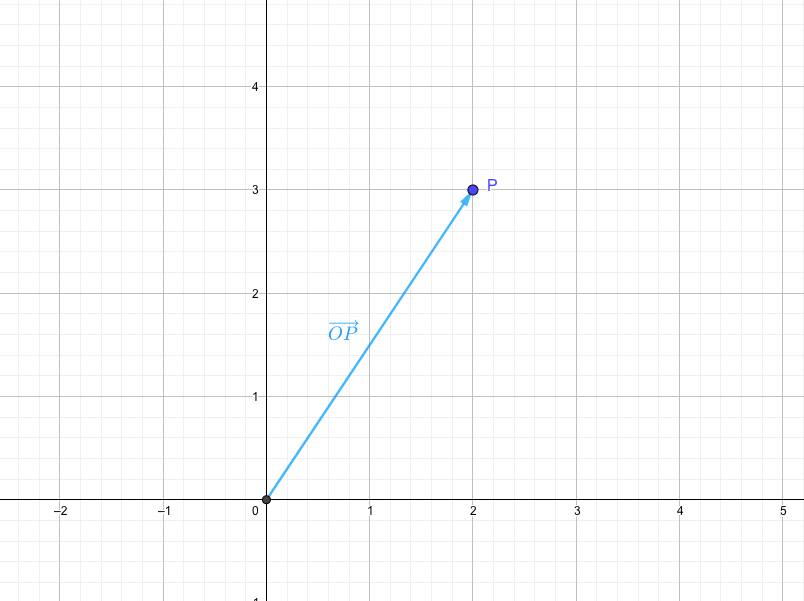
図の$\overrightarrow{OP}$の大きさは、線分$OP$の長さのことを指しています。

またこのベクトルの大きさを$|\overrightarrow{OP}|$のように表します。

小春

つまりベクトル$\overrightarrow{OP}$の大きさ$|\overrightarrow{OP}|$は、線分$OP$の長さを表しているってことね！

2点間の距離を求める際、数学では三平方の定理が大変有効です。

そこで今回も、直角三角形を意識して三平方の定理を活用してみると、

\begin{align} OP &= \sqrt{2^2+3^2}\\\ &= \sqrt{13}\\\ \end{align}

よって、

$$|\overrightarrow{OP}|=OP=\sqrt{13}$$

となります。

一般化すると、ベクトル$\overrightarrow{OP}=\begin{pmatrix}a\\ b\\ \end{pmatrix}$のベクトルの大きさ$|\overrightarrow{OP}|$は

$$|\overrightarrow{OP}|=\sqrt{a^2+b^2}$$

で求めることができる。

楓

ただしこの公式を覚えるよりも、意味を理解して欲しい！！

ベクトルの種類｜「向き」「移動距離」「場所」に着目

楓

ベクトルにはいろんな種類があって、図形を把握するツールとしてかなり便利！

逆ベクトル

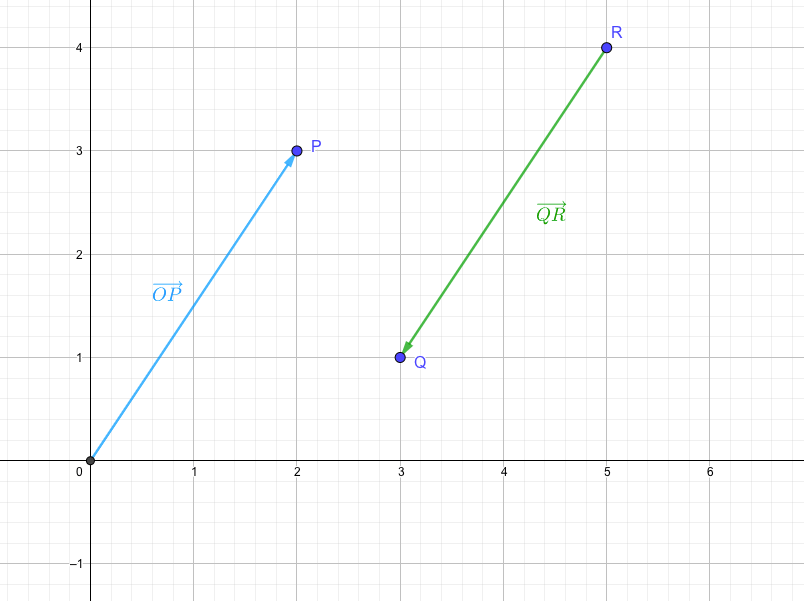
図の$\overrightarrow{OP}$に対して、逆向きの平行移動を表す$\overrightarrow{QR}$を$\overrightarrow{OP}$の逆ベクトルといい、

$$\overrightarrow{QR}=-\overrightarrow{OP}$$

のようにマイナス符号をつけて表します。

零ベクトル

ベクトル$\overrightarrow{OP}$と、その逆ベクトル-$\overrightarrow{OP}$を足してみる。

これは「行って帰ってくる」という平行移動を表し、結果的に元の位置から動いてはいないですよね。

よって元の位置から動かない平行移動を$\overrightarrow{0}$と表すものとすると、

$$\overrightarrow{OP}+\left(-\overrightarrow{OP}\right)=\overrightarrow{0}$$

が成り立ちます。

単位ベクトル

移動距離が1のベクトルのこと。

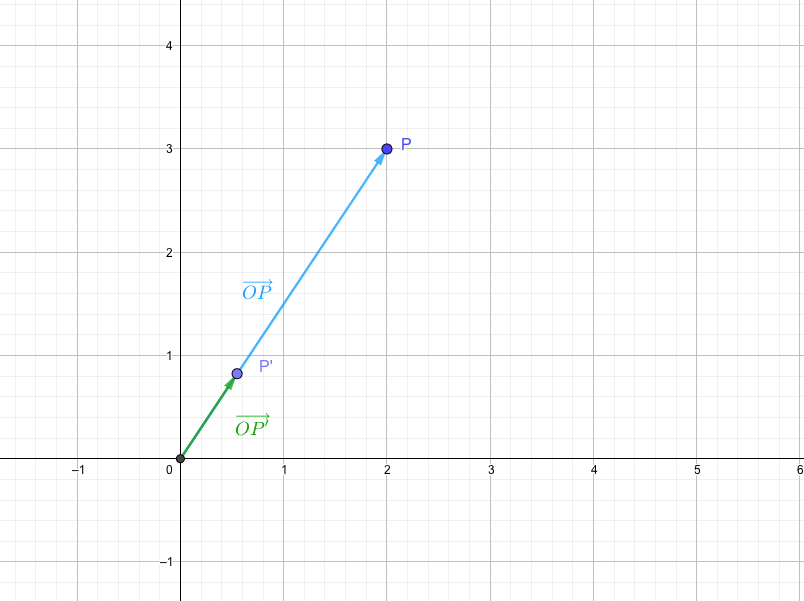
$\overrightarrow{OP}$の大きさ

$$|\overrightarrow{OP}|=OP=\sqrt{13}$$

なので、自身の大きさで割ってあげることで、求めることができます。

つまり単位ベクトル$\overrightarrow{OP'}$は

$$\overrightarrow{OP’}=\frac{\overrightarrow{OP}}{|\overrightarrow{OP}|}=\frac{\overrightarrow{OP}}{\sqrt{13}}$$

となります。

位置ベクトル

始点が原点のベクトルのこと。

$\overrightarrow{OP}$は位置ベクトルであるが、$\overrightarrow{QR}$は位置ベクトルではありません。

楓

でも平行移動の仕方的に同じベクトルだから、言葉の違いってだけ。

位置ベクトルを使うことで、平面上全ての点の位置を位置ベクトルで表すことができ、図形などを調べるときにかなり便利。

そのため使う頻度が高く、いちいち$\overrightarrow{OP}$と書くのはめんどくさいので、

$$\overrightarrow{OP}=\overrightarrow{p}$$

と省略して表すことが多いです。

また原点Oから点Pまでの平行移動は、位置ベクトル$\overrightarrow{p}$で表すことができ、このような点Pのことを

$$P(\overrightarrow{p})$$

と表記する。

方向ベクトル

ある直線に対して、平行なベクトルのこと。

図の直線$l$に対して、$\overrightarrow{OP}$と$\overrightarrow{QR}$はどちらも平行なので、両方とも直線$l$の方向ベクトルです。

小春

これ何に使うの？

実は直線の式をベクトルで表すことができるんだ。

楓

小春

ベクトルだけで表せていいことあるの？

関数では表しにくい微妙な位置の点や、空間図形における空中に浮かぶ点なんかの位置も把握できるようになるんだ！

楓

小春

つまり関数や座標とは別の観点で、点の場所を特定できるようになるってことね！

その通り！詳しくはベクトル方程式で扱うよ！

楓

法線ベクトル

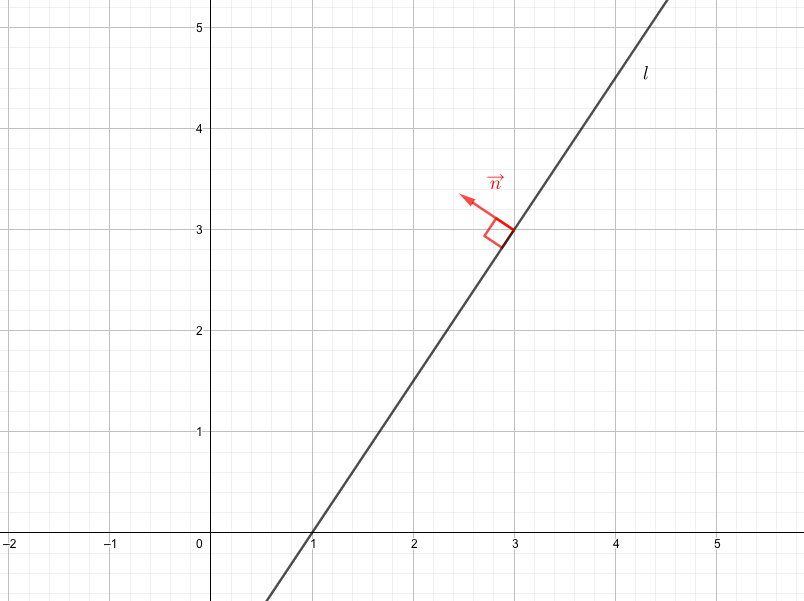
図のように、直線$l$に垂直なベクトル$\overrightarrow{n}$のことを、直線$l$の法線ベクトルという。

楓

直線$l$と垂直な関係であれば、どんなベクトルも法線ベクトルとして扱えるよ。

ベクトルを考えるメリット｜図形を数式に落とし込む

小春

ベクトルは結局、勉強することで何かメリットがあるの？

あなたは図形問題、得意ですか？

僕はかなり苦手だったんですけど、ベクトルのおかげで図形問題はなんとかクリアできるようになっていました。

しかし図形問題得意な人は、ベクトルなんか使わなくても一瞬で答えを導き出してしまいます。

この差は経験値によって作られた「図形的な才能」によって生じます。

楓

この図形的な才能の差は圧倒的で、持っている人はよく「見ればわかるじゃん」といいます。

問題でもよく「どうしてここで二等分線作図しようと思ったの？！」ってことよくあるよね・・・。

小春

しかしベクトルさえ使えれば、その「図形的な才能」を擬似的に獲得することができます。そうすることで「見ればわかるじゃん」に対して、「確かにそうだね」と返すことができる。

つまりベクトルは凡人が天才に追いつくための、図形を簡単に把握するためのツールなんです。

ベクトルを使うことで、感覚をしっかり数式に表現できるようになったわけですね。

楓

図形からベクトルという数に落とし込めると、計算処理を簡単にでき、図形をただの計算問題に変形できるようになるよ！

実践的なベクトルの例題

楓

ではどれほどベクトルが強力か見ていこう！

ここでは少し簡単な実践例を見てみましょう。

ただしあくまで見るだけ、「あぁほんとだ。答え出せてるすげー」的な感覚で見てもらえれば大丈夫です。

例題

３つの点$A(1,2),B(2,3),C(-1,1)$がある。直線ABと垂直に交わり、点Cを通るような直線の方程式を求めよ。

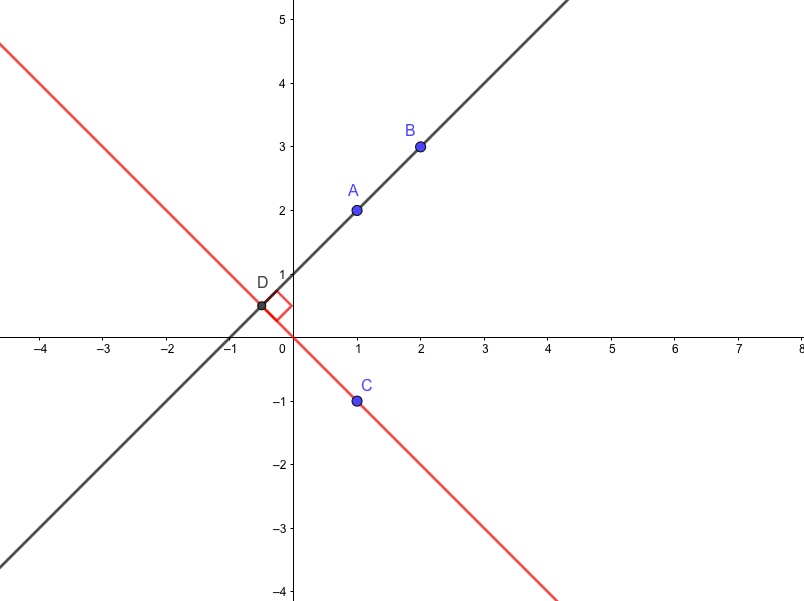
（解答）

直線ABと、点Cを通る垂直な直線の交点を$D(x,y)$とする。

$$\overrightarrow{AB}=\begin{pmatrix}2-1\\ 3-2\\ \end{pmatrix}=\begin{pmatrix}1\\ 1\\ \end{pmatrix}$$

$$\overrightarrow{CD}=\begin{pmatrix}x-(-1)\\ y-1\\ \end{pmatrix}=\begin{pmatrix}x+1\\ y-1\\ \end{pmatrix}$$

$\overrightarrow{AB}\perp\overrightarrow{CD}$なので

$$\overrightarrow{AB}\cdot\overrightarrow{CD}=0$$

よって、

$$\begin{pmatrix}1\\ 1\\ \end{pmatrix}\cdot \begin{pmatrix}x+1\\ y-1\\ \end{pmatrix} =1(x+1)+1(y-1)=0$$

（※見切れている場合はスクロール）

以上より求める直線の方程式は、

$$x+y=0$$

ベクトルを使わない解法であれば、通常は点Dの座標を求め、直線CDの方程式を導出します。

それがベクトルを使えば、点Dの座標がわからなくても答えを求めることができました。これだけでも十分価値のある概念だと思いますよ。

ベクトルのまとめ

楓

最後にまとめます。

まとめ

ベクトルとは、「平行移動」を数として考えたもの

$$\overrightarrow{OB}=\overrightarrow{OA}+\overrightarrow{AB}$$

$$\overrightarrow{AB}＝\overrightarrow{OB}+\overrightarrow{OA}$$

ベクトルの大きさは$$|\overrightarrow{OP}|=\sqrt{a^2+b^2}$$で求める。

逆ベクトル、零ベクトル、単位ベクトル、位置ベクトル、方向ベクトル、法線ベクトルは「向き」「距離」「場所」に着目している。

ベクトルは最初、取っ付きにくいイメージを持ってしまいがちですが、理解できれば図形問題がより簡単に考えることができる、大変優秀な数です。

大学数学でもこのベクトルを用いて、人間の感覚では見えない4次元以上の図形を考えたりもします。

言い換えれば、図形問題が嫌いな人ほど、マスターすべきツール。

ぜひとも使えるようになってください！

以上、「ベクトルって何？」についてでした。