これで意味は完璧！ベクトル方程式って結局何が言いたいの？→円や直線上の点Pの位置ベクトルを他の位置ベクトルで表したい

Today's Topic

$$\overrightarrow{p}=(1-s)\overrightarrow{a}+s\cdot\overrightarrow{b}$$

$$|\overrightarrow{p}-\overrightarrow{a}|=r$$

小春

楓くん、ベクトル方程式が全くわかんないんだけど・・・。

ついにベクトル方程式まで来たかぁ。

楓

小春

なに？！そんなに難しいの？！

ベクトル方程式は、少し慣れとコツが必要なんだ。でも大事な知識や、数学のイメージが飛躍的に伸びるところでもある。

楓

小春

じゃあ、じっくり丁寧にやっていけばいいのね！

そう、焦らずにね！僕もこれから丁寧に解説していくから、一つ一つしっかり理解していってね！

楓

こんなあなたへ

「ベクトル方程式の意味がわからない！」

「普通の方程式との違いって何！？」

この記事を読むと、この意味がわかる！

2つの点$A(0,4),B(2,1)$を通る直線上の任意の点$P$の位置ベクトル$\overrightarrow{p}$のベクトル方程式を求めよ。
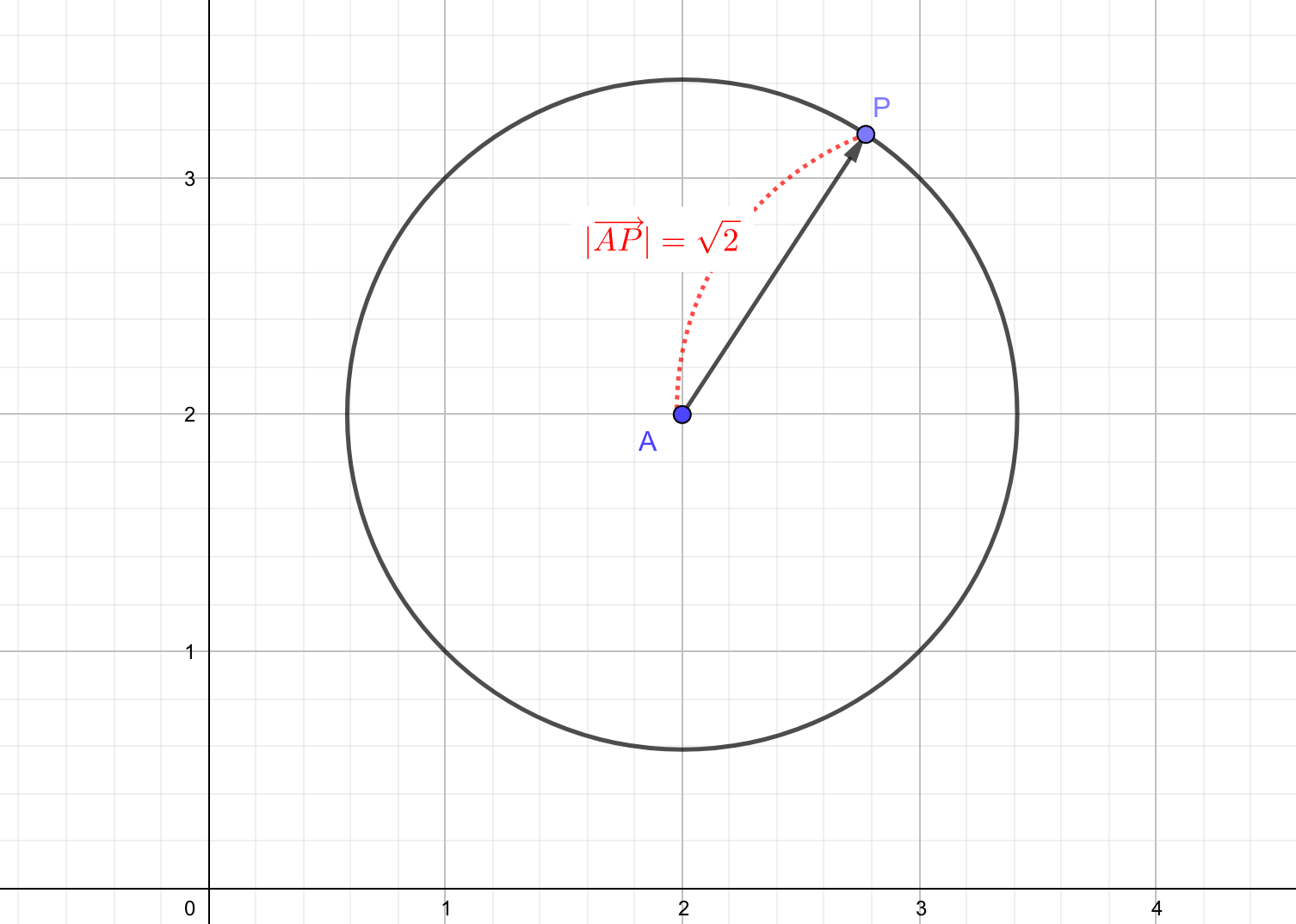
ベクトル方程式$|\overrightarrow{p}-\overrightarrow{a}|=\sqrt{2}$を満たす点$P$の位置ベクトル$\overrightarrow{p}$が描く図形を図示せよ。ただし、$\overrightarrow{a}=\begin{pmatrix}2\\ 2\\ \end{pmatrix}$とする。

小春

答えは最後にあるよ！

Contents

1 位置ベクトルという考え方
2 ベクトル方程式とは
- 2.1 ベクトル方程式の裏ワザ→成分表示
3 基本的なベクトル方程式
4 ベクトル方程式まとめ→点Pの動きを追う！

位置ベクトルという考え方

楓

ベクトル方程式に必須の『位置ベクトル』について、しっかり理解しよう！

位置ベクトルとは、ベクトルの始点が原点になっている$\overrightarrow{OP}$や、$\overrightarrow{OA}$のことを言います。

通常、$\overrightarrow{OP}=\overrightarrow{p},\ \overrightarrow{OA}=\overrightarrow{a}$のように略記します。

楓

図の$\overrightarrow{OP},\overrightarrow{OA}$は位置ベクトルだけど、$\overrightarrow{BC}$は位置ベクトルじゃないね。

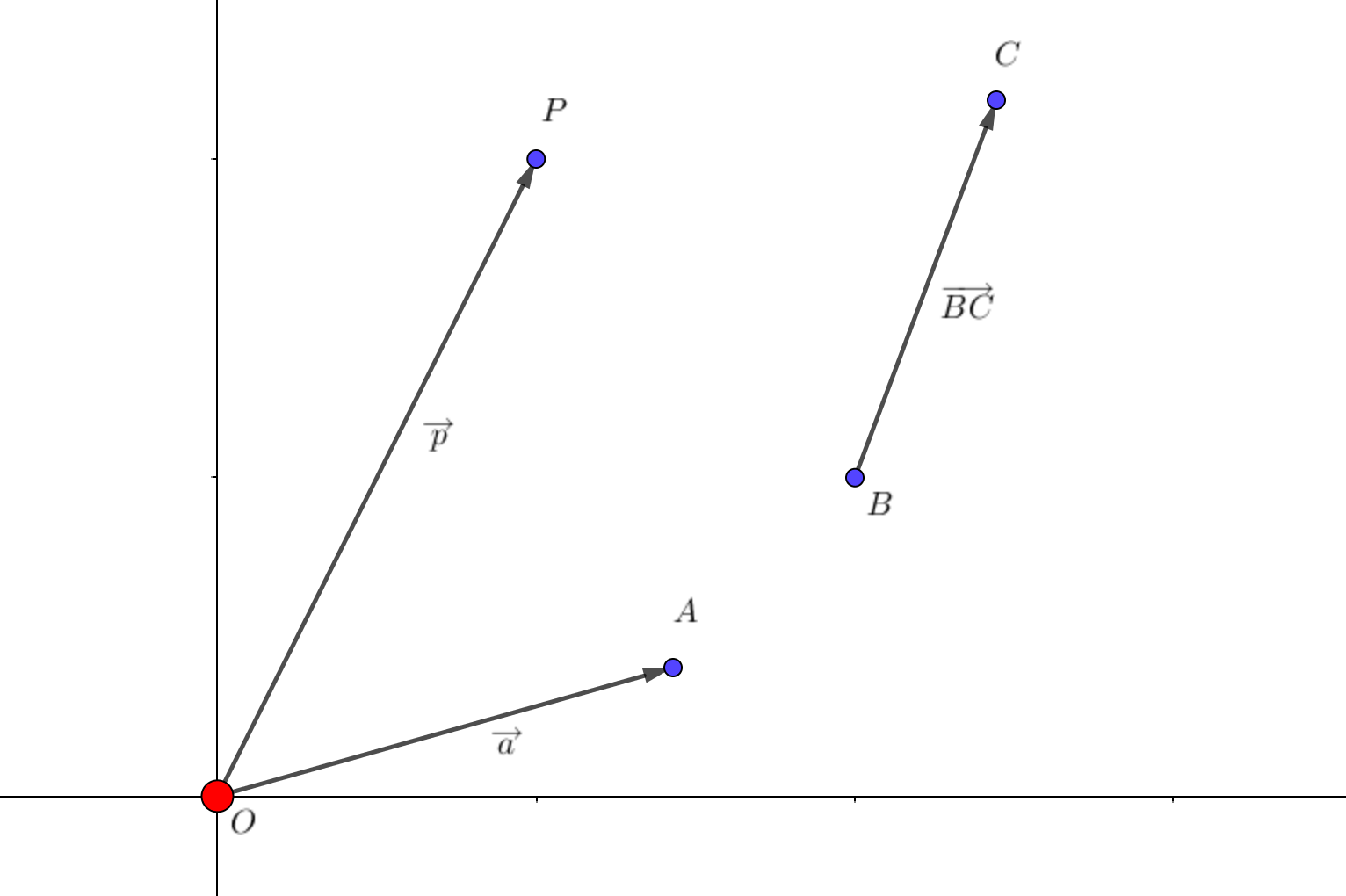
また、上図のような点$A$を『点$A(\overrightarrow{a})$』、

点$P$を『点$P(\overrightarrow{p})$』と表記することがあります。

楓

このとき『点$A$は位置ベクトル$\overrightarrow{a}$を持つ』とか言うね

位置ベクトルの利点としては、どんなベクトルも位置ベクトルの和や積で表すことができます。

例えば図の$\overrightarrow{BC}$は下の図のようにみると

$$\overrightarrow{BC}=\overrightarrow{c}-\overrightarrow{b}$$

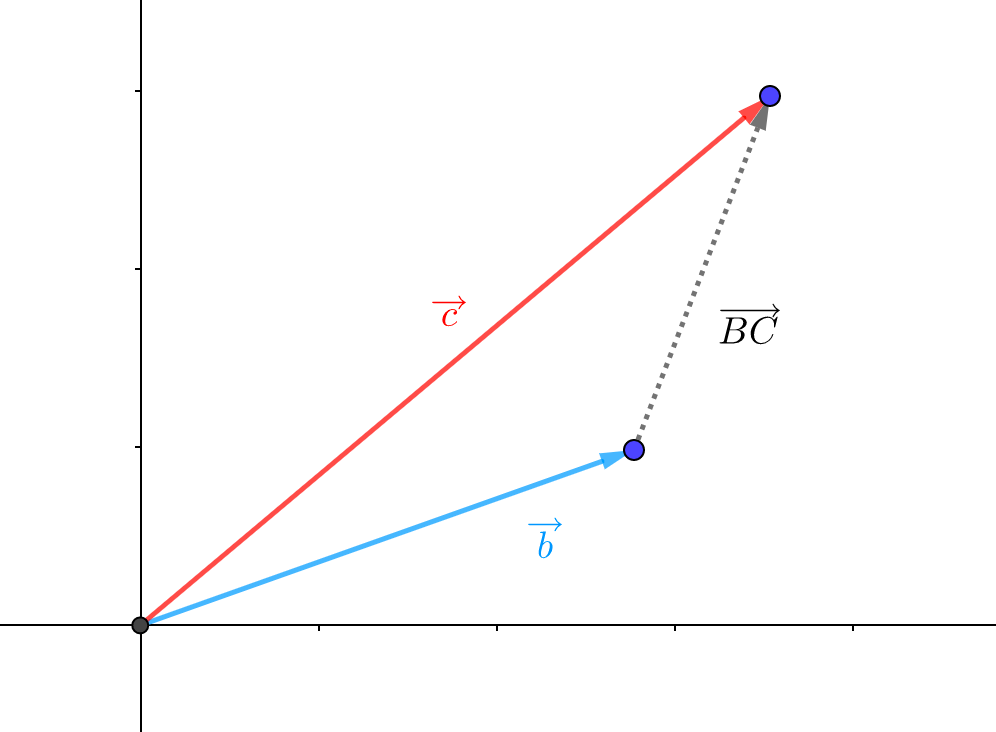
と2つの位置ベクトルに分解することができました。

ベクトル方程式とは

小春

いよいよ本題だね・・・（ゴクリ）

ベクトル方程式は、任意の点$P$の位置ベクトル$\overrightarrow{p}$を、別の位置ベクトルを用いて表現した方程式のこと。

例えば、

$$\overrightarrow{p}=s\overrightarrow{a}+t\overrightarrow{b}\ (s,tは実数)$$

は位置ベクトル$\overrightarrow{p}$を、2つの位置ベクトル$\overrightarrow{a},\overrightarrow{b}$で表現したベクトル方程式です。

このベクトル方程式は位置ベクトル$\overrightarrow{p}$の終点、つまり点$P$の動きを表現しています。

楓

逆に言えば、動く点$P$を表すのにベクトル方程式はピッタリってことだね。

・・・？？

小春

はい、なんのことかサッパリですね！

少し具体例を見てみましょう。

例題

点$A(1,1)$の位置ベクトルを$\overrightarrow{a}$とするとき、ベクトル方程式
$$\overrightarrow{p}=k\overrightarrow{a}\, (kは実数)$$
で表される点$P$の描く図形は何か。

ここから先は、一緒にグラフを描いてみよう！

与えられたベクトル方程式によると、点$P$の位置ベクトル$\overrightarrow{p}$は$\overrightarrow{a}$を実数倍したもので表せるらしいです。

$k$はどんな実数でもいいので、例として-3から3までの値をとってみましょう。

このとき位置ベクトル$\overrightarrow{p}$の終点$P$は、次のように変化していきます。

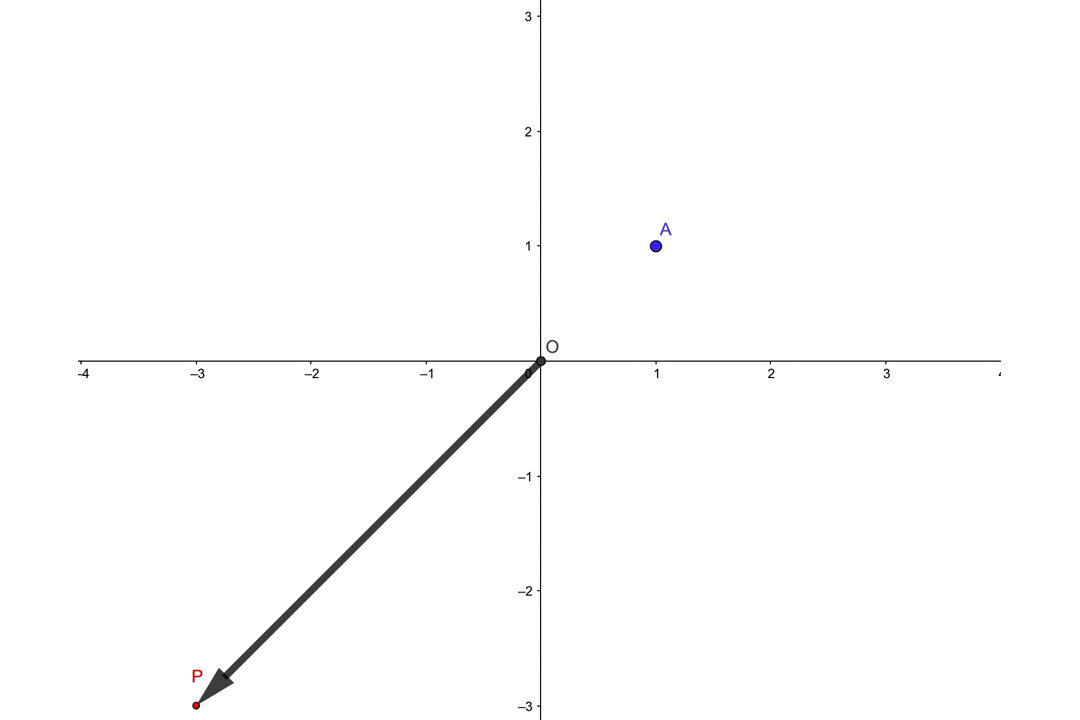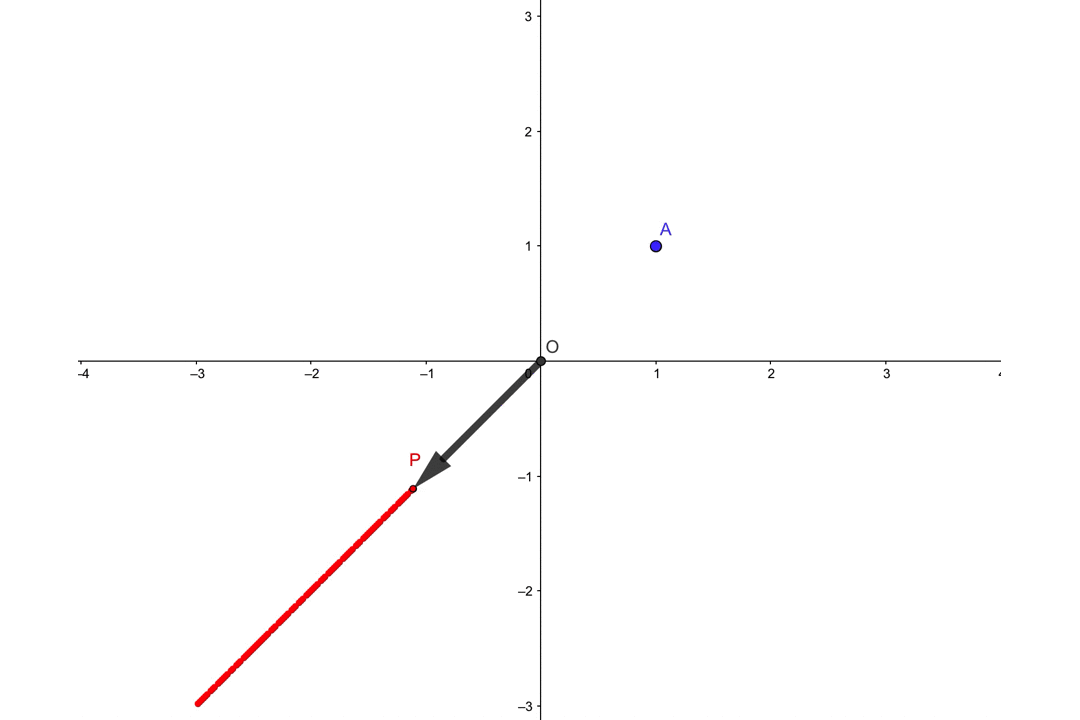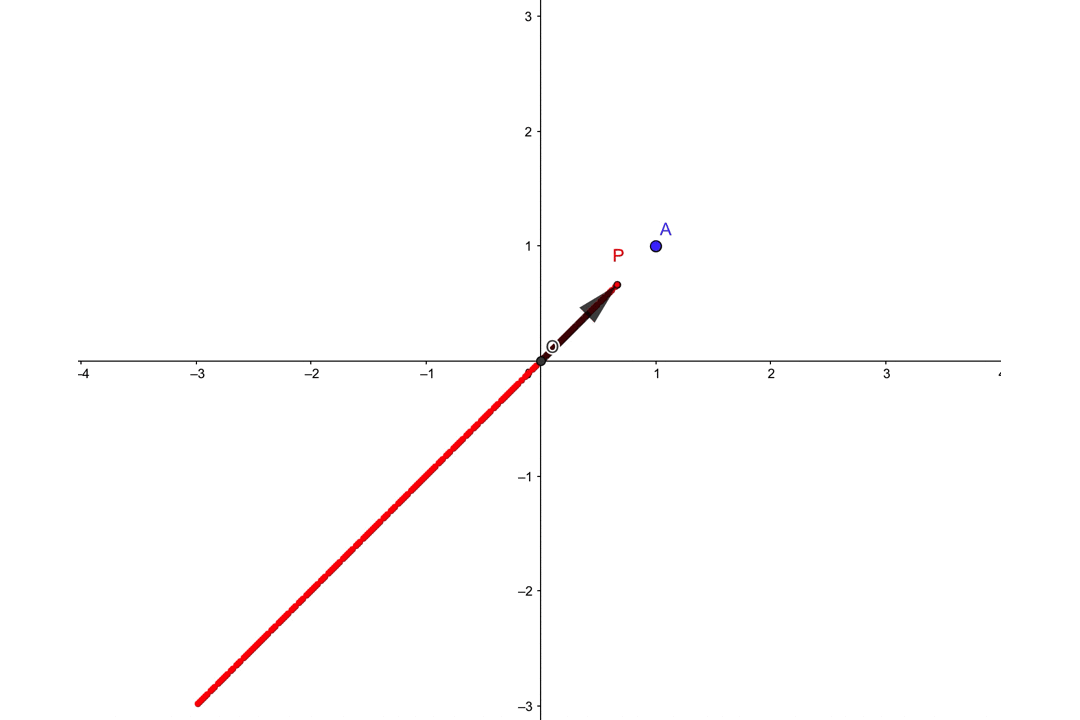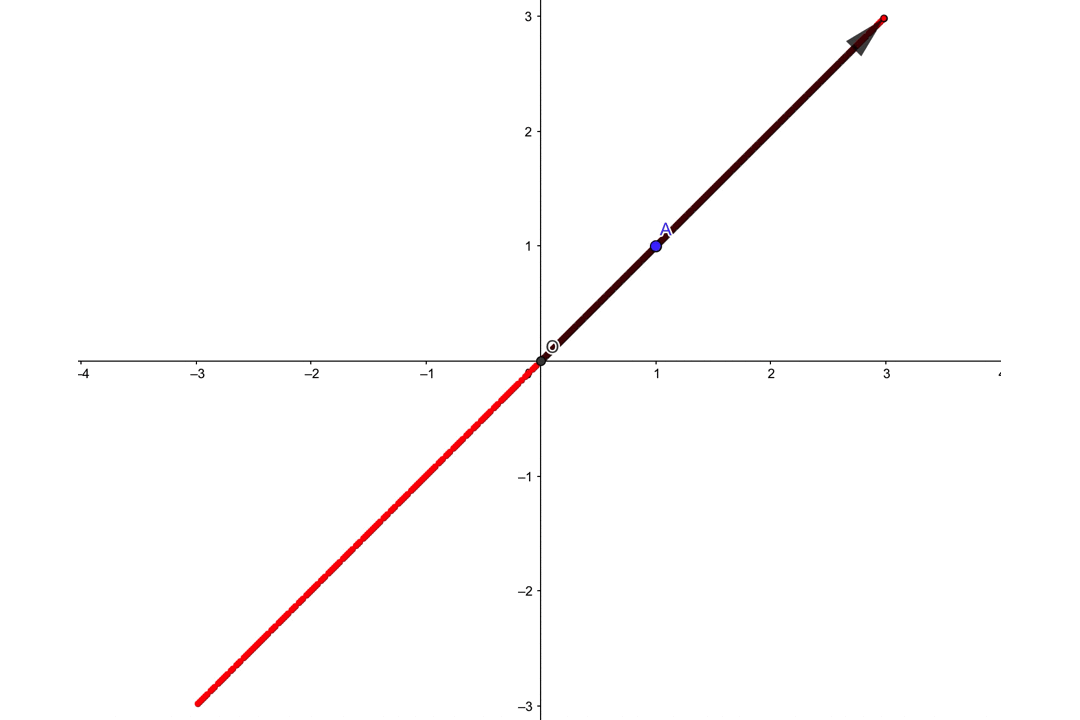
この他にも$k$は実数全体どんな数でもOKな訳ですから、無限個の点$P$を描いていくと、図のように直線になると思われます。

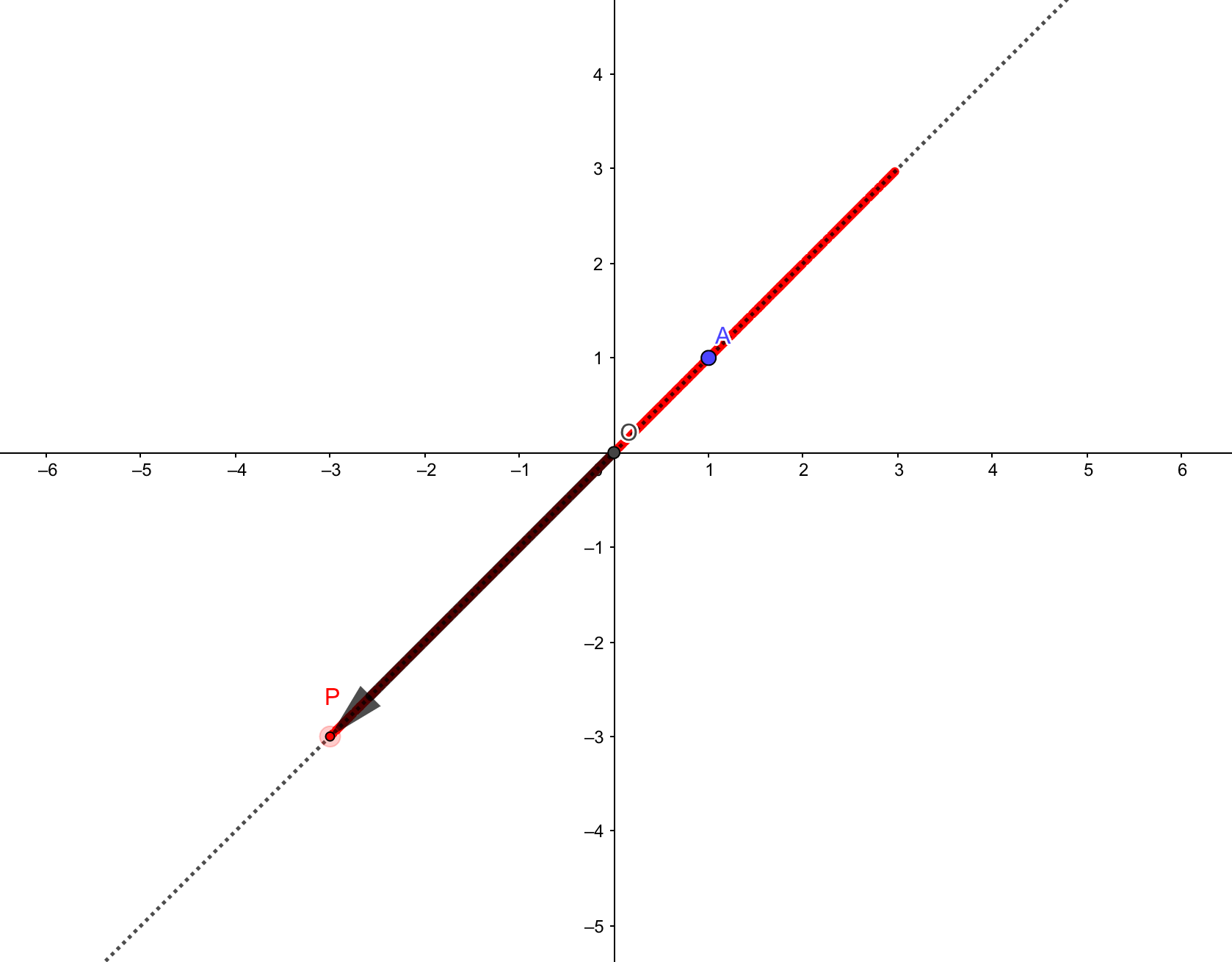
つまり、

ポイント

任意の位置ベクトル$\overrightarrow{a}$を用いて、位置ベクトル$\overrightarrow{p}$がベクトル方程式

$$\overrightarrow{p}=k\overrightarrow{a}\, (kは実数)$$

を満たすとき、点$P$は原点と点$A$を通る直線を描く。

ということがわかります。

楓

これは暗記することじゃなくて、ベクトルをイメージするとこういうことがいえるって話ね。

ベクトル方程式の裏ワザ→成分表示

点$P$の位置ベクトルの成分を、

$$\overrightarrow{p}=\begin{pmatrix}x\\ y\\ \end{pmatrix}$$

としてみましょう。

この$x$成分と$y$成分の関係が分かれば、与えられたベクトル方程式を今まで慣れ親しんだ関数や方程式の形に直すことができます。

実際に直してみましょう。

点$A$の位置ベクトルの成分は座標を見れば、

$$\overrightarrow{a}=\begin{pmatrix}1\\ 1\\ \end{pmatrix}$$

とわかります。

楓

位置ベクトルと座標は、一緒とみなしていいよ。

ベクトル方程式$\overrightarrow{p}=k\overrightarrow{a}\, (kは実数)$より、

\begin{align} \begin{pmatrix}x\\ y\\ \end{pmatrix} &= k\begin{pmatrix}1\\ 1\\ \end{pmatrix}\\\ &= \begin{pmatrix}k\\ k\\ \end{pmatrix}\\\ \end{align}

これにより、

$$\left\{ \begin{array}{l} x=k \\ y=k \end{array} \right. $$

が成り立つので、代入して

$$y=x$$

が得られます。

これは先ほど、ベクトル方程式を図で考えたときに得た直線の方程式になっていますね。

小春

原点と点$A(1,1)$を通る直線の方程式だね！

今回の結果からベクトル方程式を成分表示で考えると、今までの方程式の形にできるってことね！後で詳しく解説するよ。

楓

基本的なベクトル方程式

小春

なんかベクトル方程式、分かったようなわからないような。。。

ここからはベクトル方程式の基本が身につく「直線」と「円」のベクトル方程式を見ていこう。

楓

小春

公式を覚えれば身につくの？

そうじゃない！どうしてその公式が導出されているかを考えるんだ！

楓

直線のベクトル方程式

ベクトル方程式

$$\overrightarrow{p}=(1-s)\overrightarrow{a}+s\overrightarrow{b}\ (sは実数)$$

は、2つの点$A,B$を通る直線を描く点$P$の動きを表しています。

小春

なんでこれが直線になるの？

ここで2つの点$A,B$を通る直線上の点$P$について考えてみましょう。

図のように$\overrightarrow{AP}$が伸び縮みすることで、直線$AB$を表現することができそうです。

イメージはこんな感じ

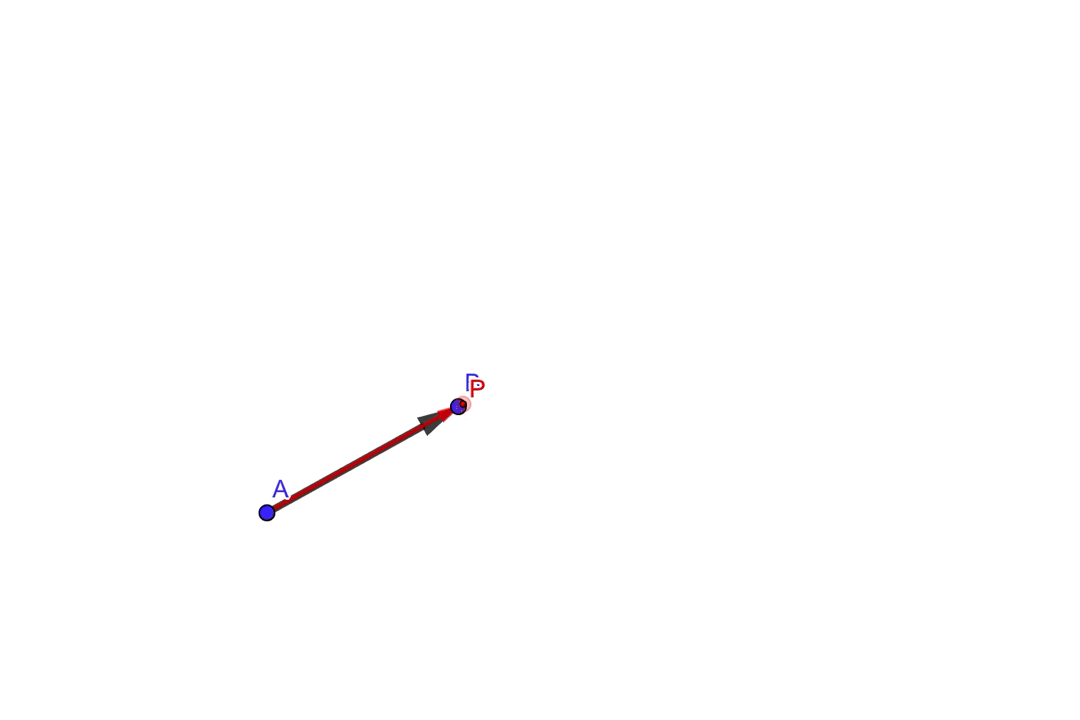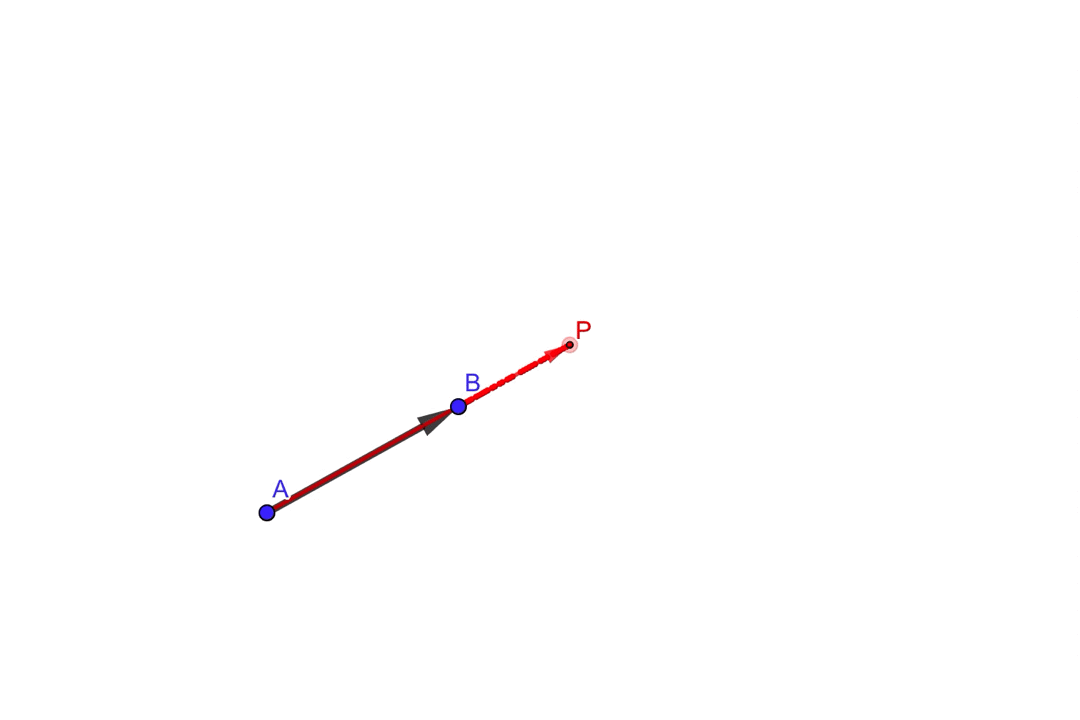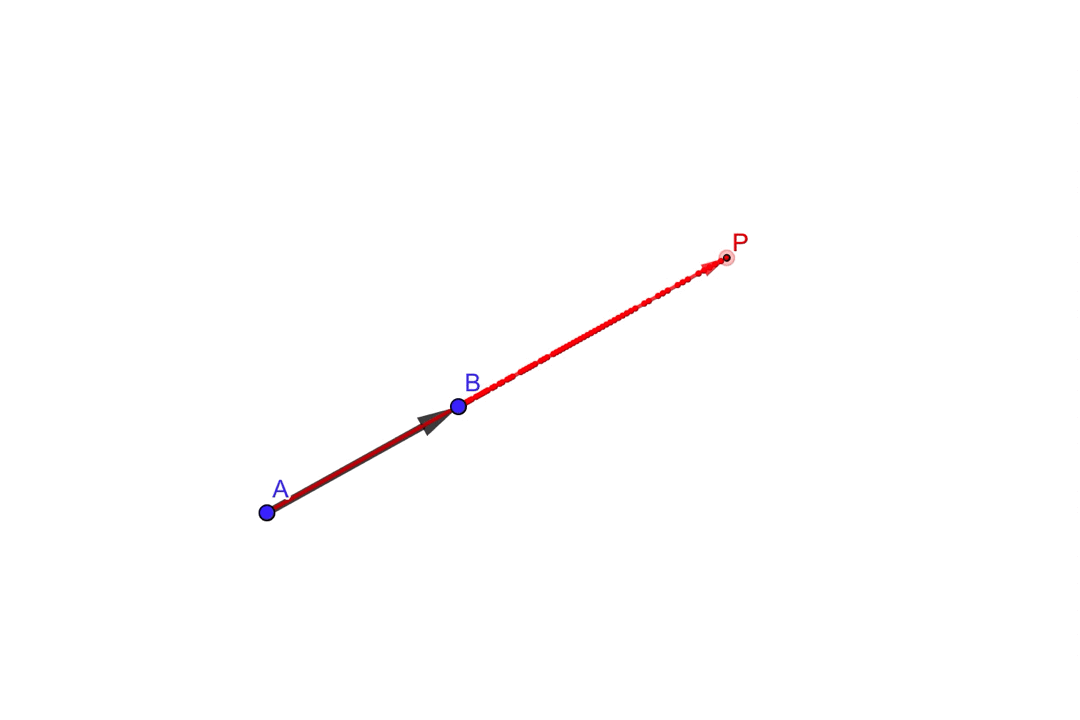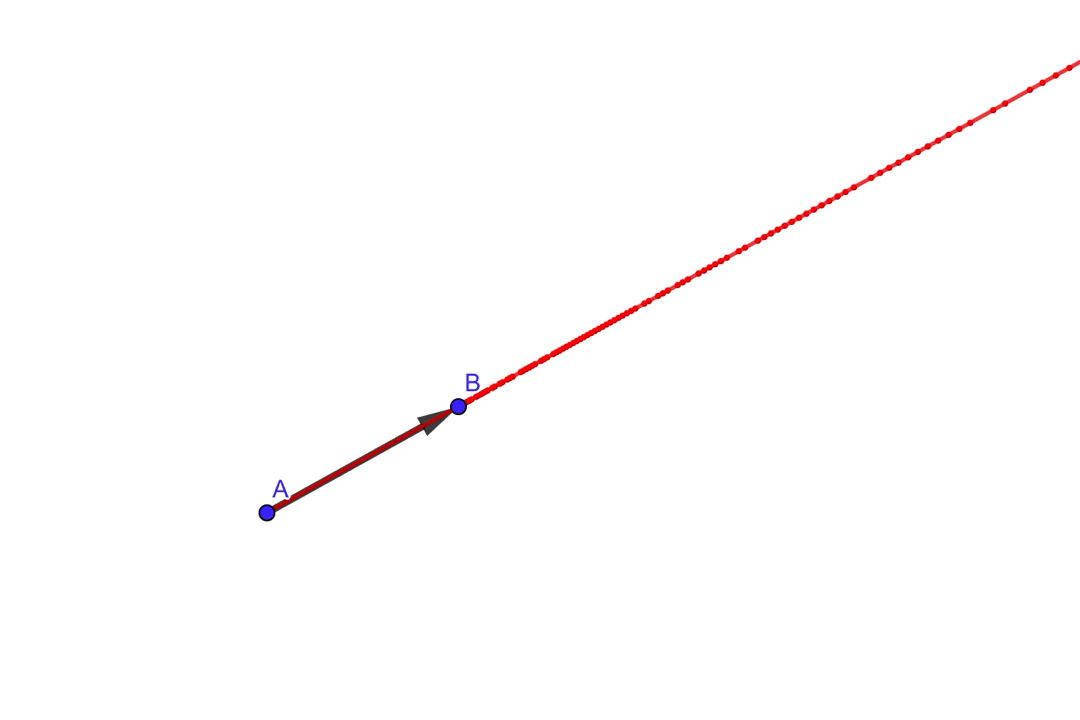
ベクトル$\overrightarrow{AP}$は、ベクトル$\overrightarrow{AB}$を定数倍することで、伸び縮みを表現できそうなので、

$$\overrightarrow{AP}=s\cdot \overrightarrow{AB}\ (sは実数)$$

と表してみます。

小春

負の実数をかけるとAの方向にも伸びるから、これは直線ABを表していることになるね。

知りたいのは点$P$の位置ベクトル$\overrightarrow{p}$なので、

$$\overrightarrow{AP}=\overrightarrow{p}-\overrightarrow{a}$$

を利用すると

$$\overrightarrow{p}-\overrightarrow{a}=s\left(\overrightarrow{b}-\overrightarrow{a}\right)$$

となるので、整理して

$$\overrightarrow{p}=(1-s)\overrightarrow{a}+s\cdot\overrightarrow{b}$$

となりました。

これが2点$A,B$を通る直線のベクトル方程式になります。

楓

ベクトル方程式は、このように簡単なベクトルの関係から求めればいいよ！

直線のベクトル方程式の成分表示

ベクトル方程式を成分表示で考えると、慣れ親しんだ方程式の形にすることができましたね。

そこで

$$\overrightarrow{p}=\begin{pmatrix}x\\ y\\ \end{pmatrix},\overrightarrow{a}=\begin{pmatrix}a_x\\a_y\\ \end{pmatrix},\overrightarrow{b}=\begin{pmatrix}b_x\\ b_y\\ \end{pmatrix}$$

として、先ほどのベクトル方程式の成分表示を考えてみましょう。

$$\overrightarrow{p}=(1-s)\overrightarrow{a}+s\cdot\overrightarrow{b}$$

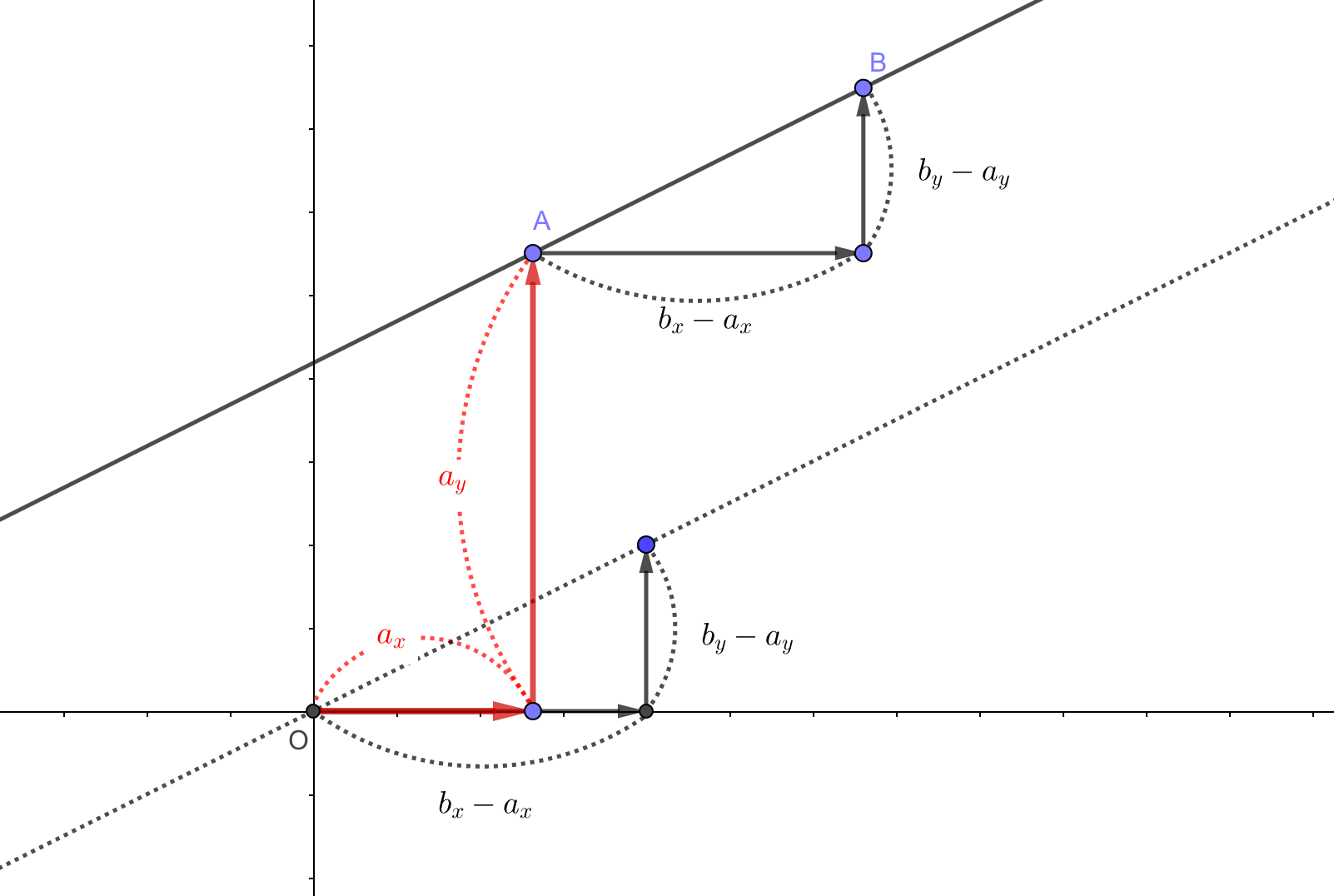
を成分表示してみると、

$$\begin{pmatrix}x\\y\\ \end{pmatrix}=(1-s)\begin{pmatrix}a_x\\a_y\\ \end{pmatrix}+s\begin{pmatrix}b_x\\b_y\\ \end{pmatrix}$$

となるので、連立方程式

$$\left\{ \begin{array}{l} x=(1-s)a_x+sb_x \\ y=(1-s)a_y+sb_y \end{array} \right. $$

が成り立ちます。

ここで、上の$x$の式を$s$について変形すると、

$$s=\frac{x-a_x}{b_x-a_x}$$

となります。

$y$の式を整理してみると、

\begin{align} y &= (1-s)a_y+sb_y\\\ &= \left(b_y-a_y\right)s+a_y\\\ \end{align}

となるので、これに先程の$s$の式を代入してみると、

$$y=\left(b_y-a_y\right)\cdot\frac{x-a_x}{b_x-a_x}+a_y$$

最後に$a_y$を移項して整理してあげると、

$$y-a_y=\frac{b_y-a_y}{b_x-a_x}\cdot\left(x-a_x\right)$$

となり、直線$y=\frac{b_y-a_y}{b_x-a_x}x$が横に$a_x$、縦に$a_y$だけ平行移動した直線の式が得られます。

楓

この直線は2点$A,B$を通る直線を表しているね！

平行移動について復習したい人はこちらを参考にしてください。

: 平行移動のやり方と公式の意味→符号を入れ替えて書き換えるだけで、グラフの問題がスラスラ解ける

続きを見る

円のベクトル方程式

ベクトル方程式

$$|\overrightarrow{p}-\overrightarrow{a}|=r$$

は中心が点$A(\overrightarrow{a})$、半径$r$の円を表しています。

これは原点が中心の円を考えてみるとわかりやすいです。

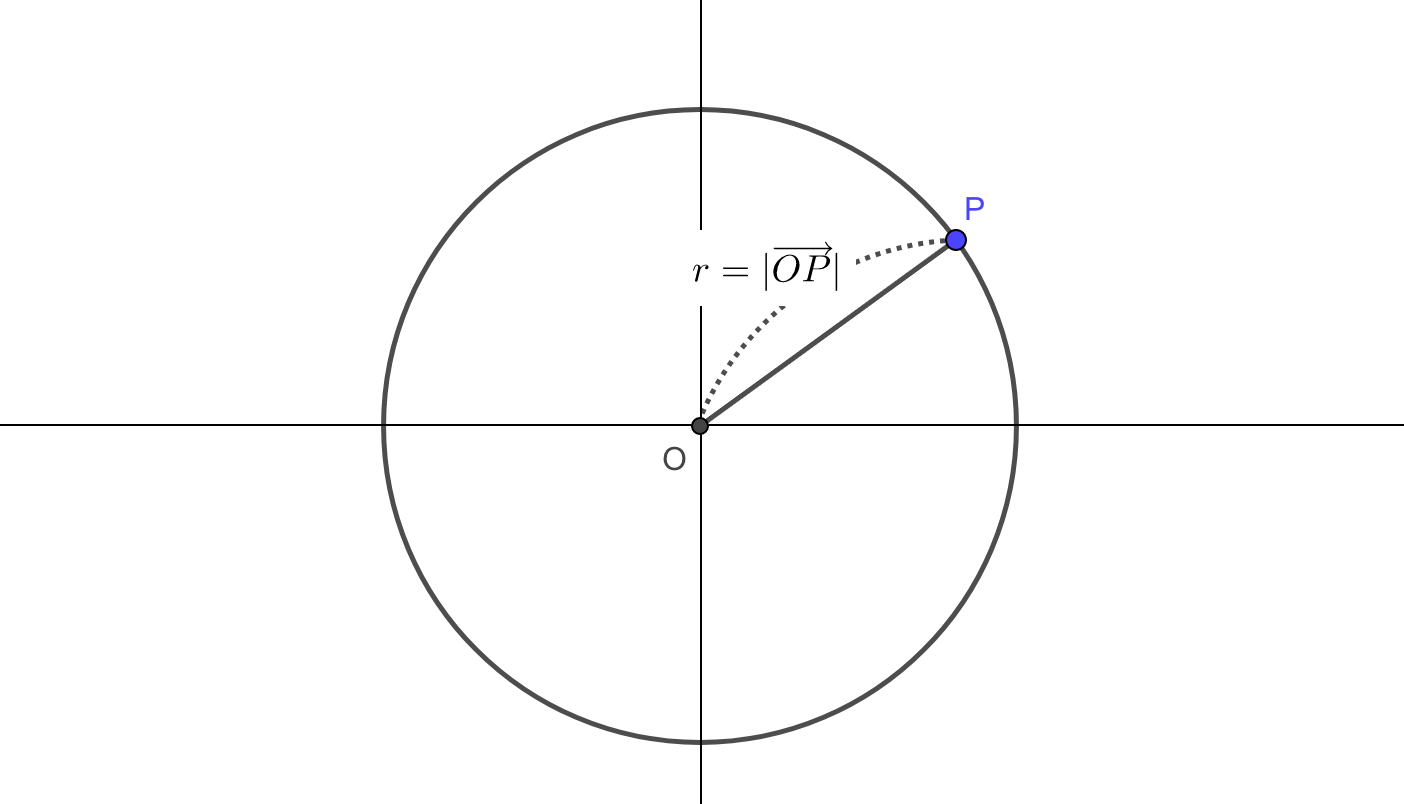
中心点から円周までの距離は一定なので、原点から円周上の点$P$までの距離は変わりません。

つまり位置ベクトルの大きさ$|\overrightarrow{p}|$は常に一定ということです。

そして円の中心から円周までの一定距離のことを半径というので、

$$|\overrightarrow{p}|=r$$

が原点中心、半径$r$の円を表しています。

この中心を点$A$にズラしてみましょう。

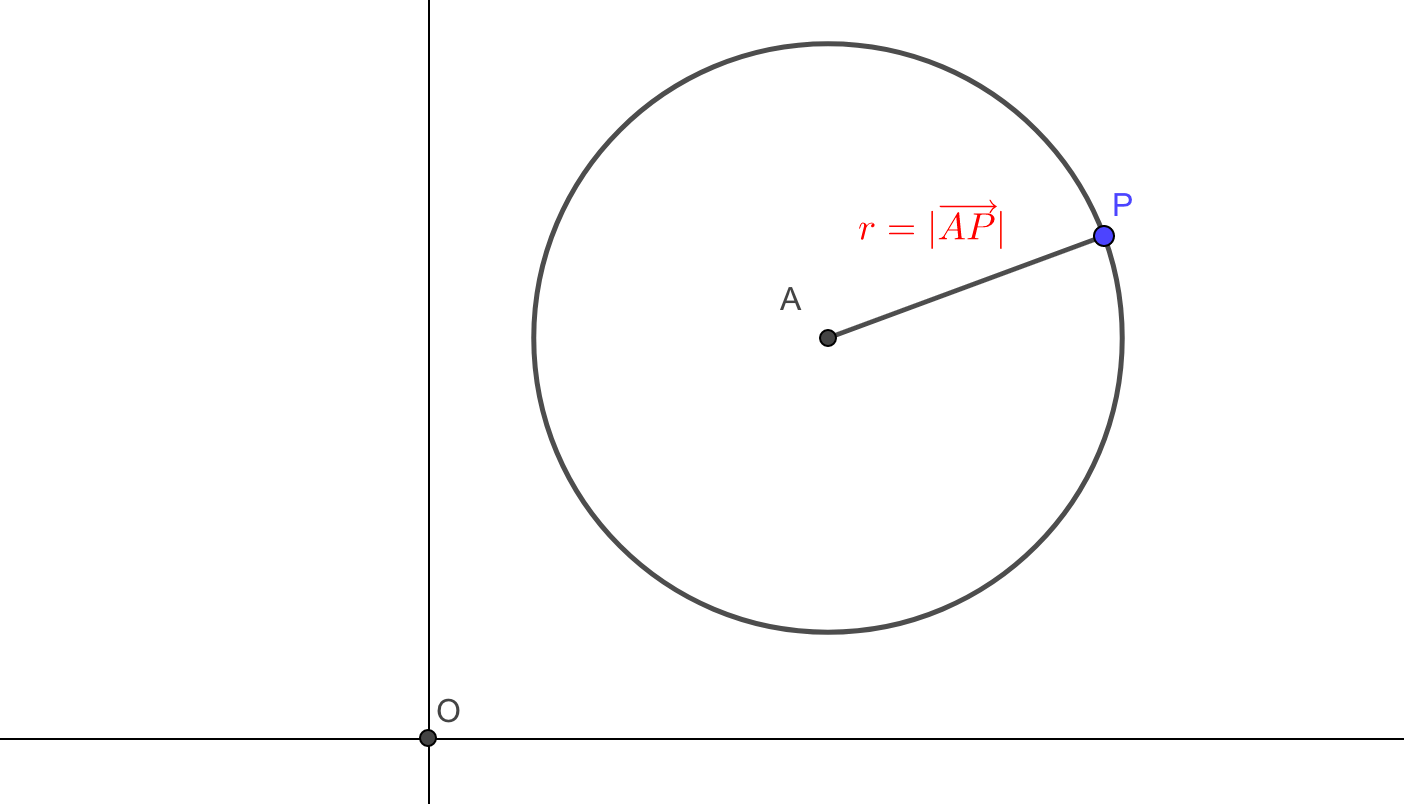
中心から円周までの距離（半径）は常に一定であるということに着目すると

$$|\overrightarrow{AP}|=r$$

が成り立つことがわかります。

これを位置ベクトルに分解してあげると、

$$|\overrightarrow{p}-\overrightarrow{a}|=r$$

が円の方程式であることがわかります。

楓

つまりこっちのベクトル方程式は、中心が任意の点なんだね。

円のベクトル方程式の成分表示

小春

ベクトル方程式は成分表示して整理すると、わかりやすくなるんだったね

$$\overrightarrow{p}=\begin{pmatrix}x\\ y\\ \end{pmatrix},\overrightarrow{a}=\begin{pmatrix}a_x\\a_y\\ \end{pmatrix}$$

として、円のベクトル方程式を考えてみましょう。

$$|\overrightarrow{p}-\overrightarrow{a}|=r$$

より、

\begin{align} \left|\begin{pmatrix}x\\ y\\ \end{pmatrix}-\begin{pmatrix}a_x\\a_y\\ \end{pmatrix}\right| &= \left|\begin{pmatrix}x-a_x\\ y-a_y\\ \end{pmatrix}\right|\\\ &= r\\\ \end{align}

小春

ここからどう式変形すればいいの？

ここから先の式変形はよく出てくるから、要チェック！

楓

ここで両辺を2乗してあげます。

楓

ベクトルの世界で絶対値出たら、とりあえず二乗しておけばいい気がする。

するとベクトルの大きさの二乗は、そのベクトル同士の内積に等しい、つまり

$$|\overrightarrow{p}|^2=\overrightarrow{p}\cdot\overrightarrow{p}=x^2+y^2$$

が成り立つので、

\begin{align} \left|\begin{pmatrix}x-a_x\\ y-a_y\\ \end{pmatrix}\right|^2 &= \begin{pmatrix}x-a_x\\ y-a_y\\ \end{pmatrix}\cdot\begin{pmatrix}x-a_x\\ y-a_y\\ \end{pmatrix}\\\ &= (x-a_x)^2+(y-a_y)^2\\\ \end{align}

（※見切れている場合はスクロール）

が成り立ちます。

これは中心が$\left(a_x,a_y\right)$、半径$r$の円を表していますね。

ベクトル方程式まとめ→点Pの動きを追う！

楓

ではまとめますー

まとめ

ベクトル方程式とは点$P$の位置ベクトル$\overrightarrow{p}$の動きを、他の位置ベクトルを用いて表現したもの。

ベクトル方程式を今まで学んだ方程式に直すためには、成分表示を考えれば良い。

【2点$A,B$を通る直線のベクトル方程式】

$$\overrightarrow{p}=(1-s)\overrightarrow{a}+s\cdot\overrightarrow{b}$$

【中心$A$で半径$r$の円】

$$|\overrightarrow{p}-\overrightarrow{a}|=r$$

今回はベクトル方程式の基本を扱いました。

この記事では

ベクトル方程式が何を意味していているのか→点$P$の動きを他の位置ベクトルで表したい！

という位置ベクトルの意味を抑えてもらえれば十分です。

小春

でも、ベクトル方程式って考えて何かいいことあるの？

メリットや使う場面については、別の記事で取り扱うね！

楓

小春

焦らずじっくり、だったね。まずは基本からしっかりしよう。

以上、「ベクトル方程式の意味と、基本的な公式」についてでした。

最初の答え
Q. 2つの点$A(0,4),B(2,1)$を通る直線上の任意の点$P$の位置ベクトル$\overrightarrow{p}$のベクトル方程式を求めよ。

直線上に点$P$があると考えてみよう！

直線$AB$上に点$P$があるとき、ベクトル$\overrightarrow{AP}$はベクトル$\overrightarrow{AB}$の実数倍で表すことができる。
つまり、
$$\overrightarrow{AP}=s\overrightarrow{AB}\ (sは実数)$$
これを位置ベクトル$\overrightarrow{p}$について解くと
$$\overrightarrow{p}=(1-s)\overrightarrow{a}+s\cdot\overrightarrow{b}$$
成分表示で考えると、
$$y-4=-\frac{3}{2}x$$
となるので、これは2点$A,B$を通る直線を表していることがわかる。

Q. ベクトル方程式$|\overrightarrow{p}-\overrightarrow{a}|=\sqrt{2}$を満たす点$P$の位置ベクトル$\overrightarrow{p}$が描く図形を図示せよ。ただし、$\overrightarrow{a}=\begin{pmatrix}2\\ 2\\ \end{pmatrix}$とする。