Today's Topic
樹形図の枝分かれが均等なとき、積の法則が適用でき、そうでないときは場合わけして和の法則を使う。






こんなあなたへ
「場合の数の意味がわからない。何をしたいの?」
「和の法則と積の法則はなぜ成り立つの?」
この記事を読むと、この意味がわかる!
- 2つのサイコロを投げた時、サイコロの目の出方は何通りあるか。
- 2つのサイコロを投げた時、サイコロの目の和が5、もしくは6となるのは何通りか。

Contents
そもそも場合の数とはなんだろう。→何通りの場合が考えられるか。
まず最初に『場合の数』なんていう、不気味な言葉について考えてみましょう。
カンタンに訳すと、
『何か実験をしたときに、どんなパターンが何通り起こり得るかな?』
を考えた数が、場合の数です。
例えば、サイコロを1つ転がす実験をしてみましょう。
すると起こり得るパターンは
- 1の目がでた。
- 2の目がでた。
- 3の目がでた。
- 4の目がでた。
- 5の目がでた。
- 6の目がでた。
の6パターンではないでしょうか。

ただし、ここで肝心なのは、考えられるパターンを全て列挙する必要があるということです。
全て列挙するためには、考えられるパターンを『モレなく、ダブりなく』数える必要があります。
例えば先ほどのサイコロの例で、『6の目がでた』場合を数え忘れていたら、場合の数は5通りとなり、正しい場合の数とは言えません。
また『1の目がでた』を2回ダブって数えてしまうと、場合の数は7通りとなり、これまた正しい場合の数とは言えません。
今回の例ではそれほどモレやダブりが発生することはないと思いますが、次の例題はどうでしょうか。
例題1
サイコロを2回転がすとき、目の出方のパターンは何通りあるか。
1回目のサイコロが1のとき、2回目のサイコロは1の場合もあれば2の場合もあります。もちろん3〜6の場合も。
じゃあ1回目のサイコロが2のときは?3のときは?


というわけで、モレやダブりが発生しないように、効率的にスッキリと数える必要があるわけです。
モレなくダブりなく数えたい→樹形図の活用
最も原始的な『効率的な数え方』の1つに、樹形図を描くという手法があります。
中学でもやった通り、樹形図とは1つの選択に対して何通りの選択肢が考えられるかを図で表したものです。
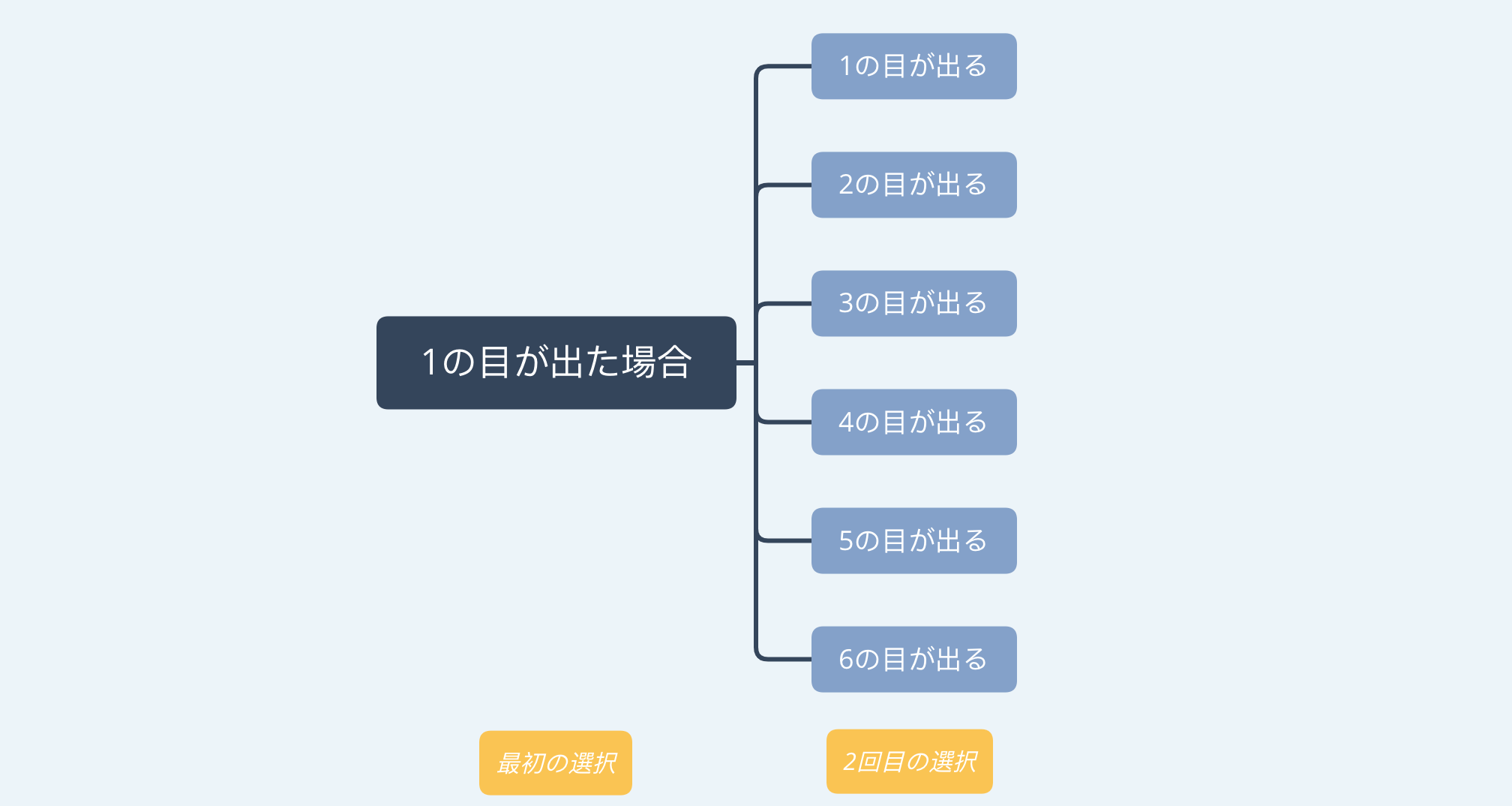

では2回サイコロを転がした際に考えられる全てのパターンは、何通りなのでしょうか。
樹形図を利用して考えてみると、
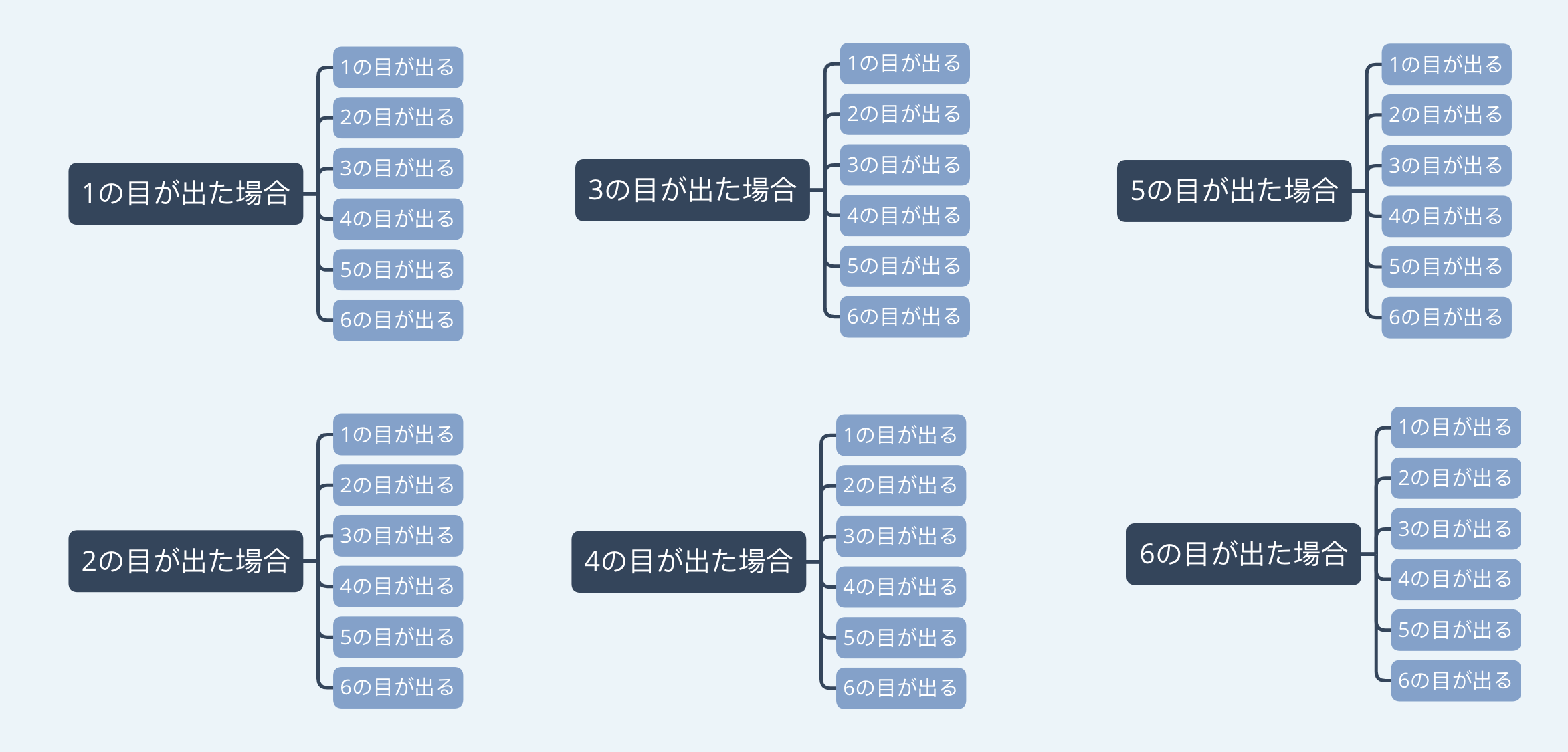


積の法則とはなんだろう。→効率よく数えたい。
ただし樹形図にも弱点があります。
それは
- とにかく描くスペースが必要。
- 選択肢が増えるほど、枝分かれが増えて書きにくいし見えにくくなる。
という点です。

そこで、先ほどの樹形図を見て何か規則性がないか考えてみましょう。



では次の例題はどうでしょうか。
例題2
4人の生徒A,B,C,Dを1列に並べる際、順番の並び方は何通りあるか。
例えばAさんを先頭にした場合、樹形図はこのように描けます。
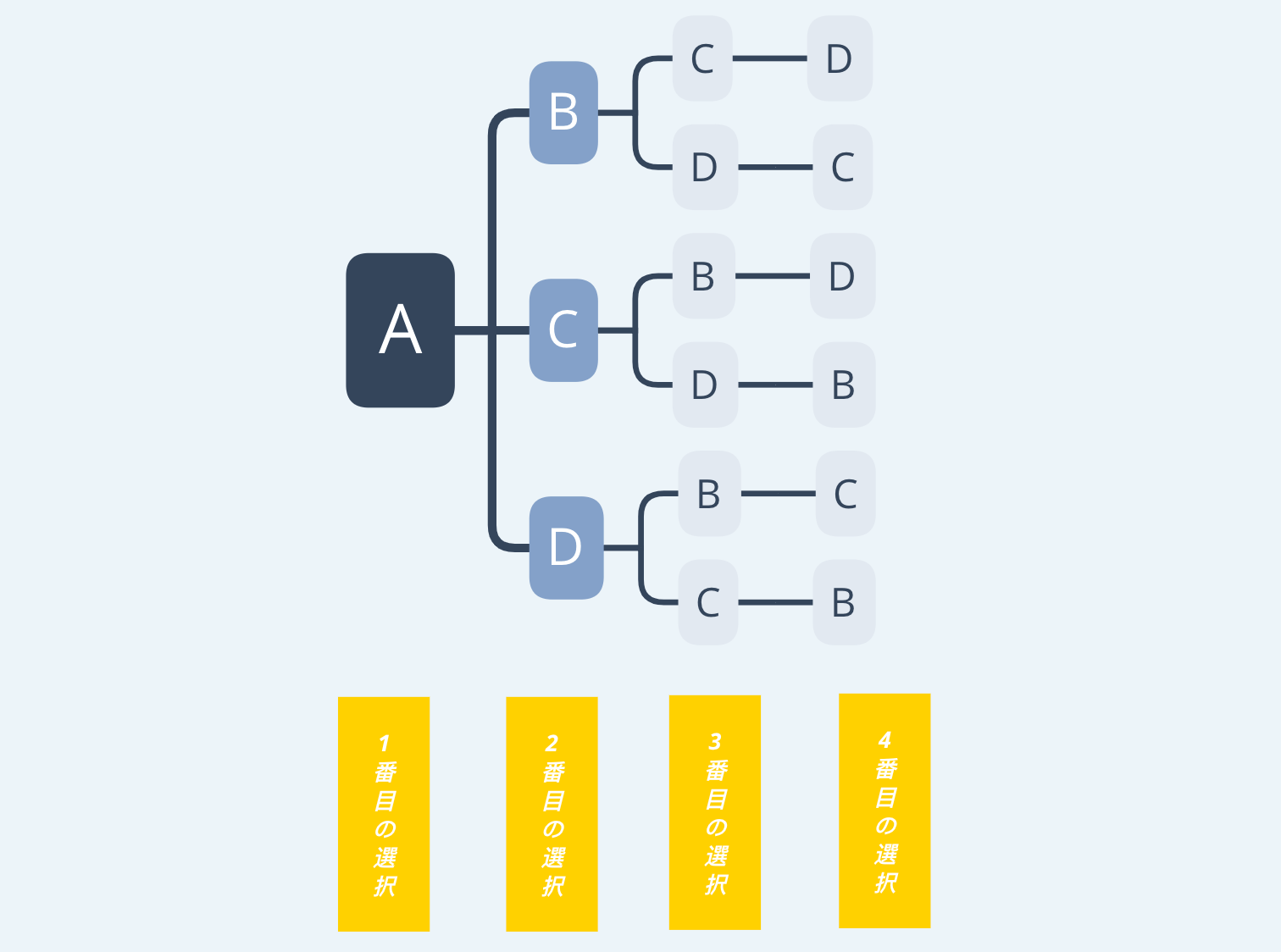


ではここで規則性を探す際のポイントを見てみましょう。
規則性を探すポイント
枝分かれしているところに着目し、1つの選択肢に対して何通りの枝分かれがあるかを考えよう。
まずAから分岐した3つの選択肢。これらはそれぞれ2つに分岐します。
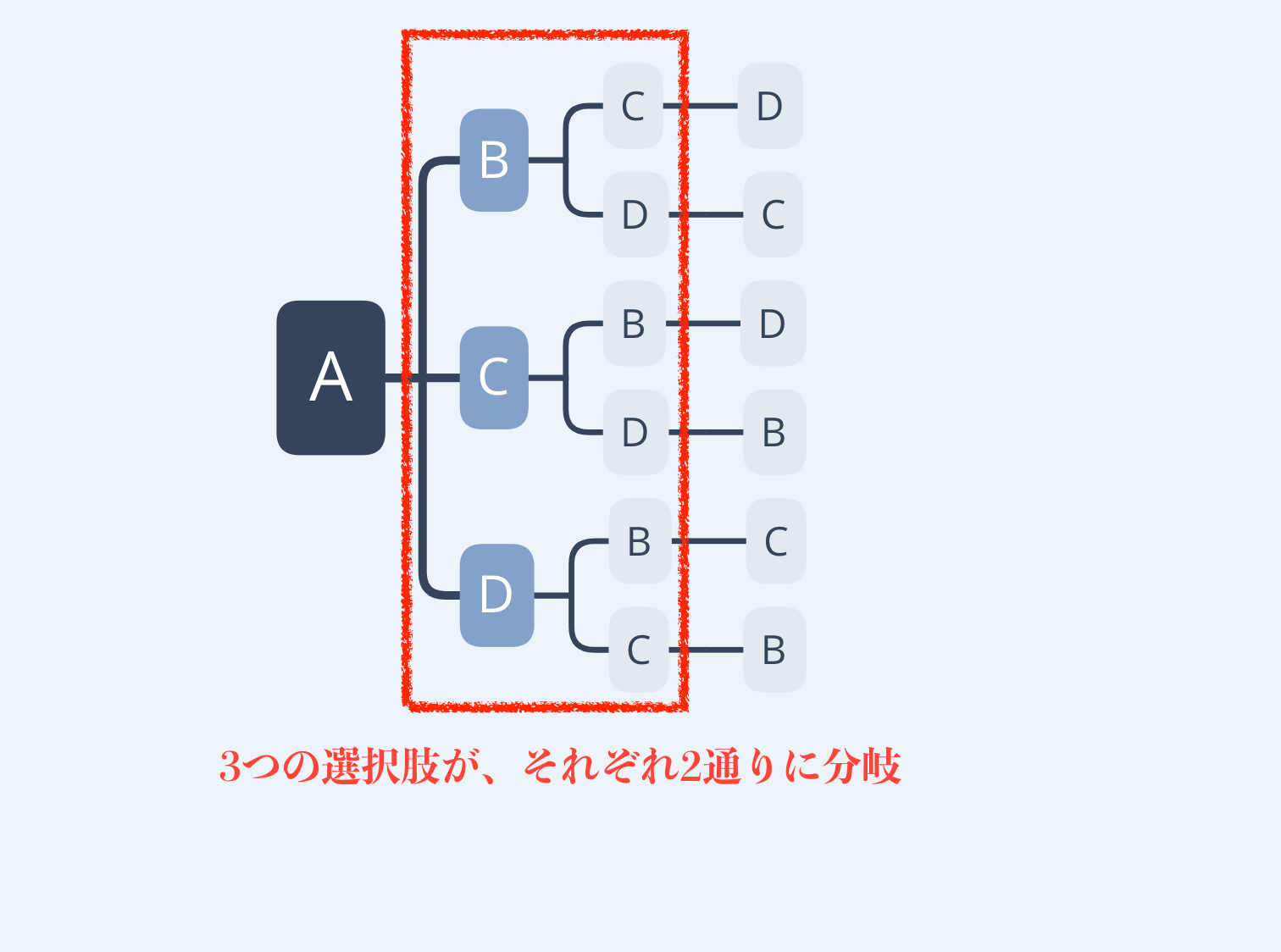


3つの選択肢から分岐した、2つのそれぞれの選択肢は分岐することなく、最後のひとを1通りに決めています。
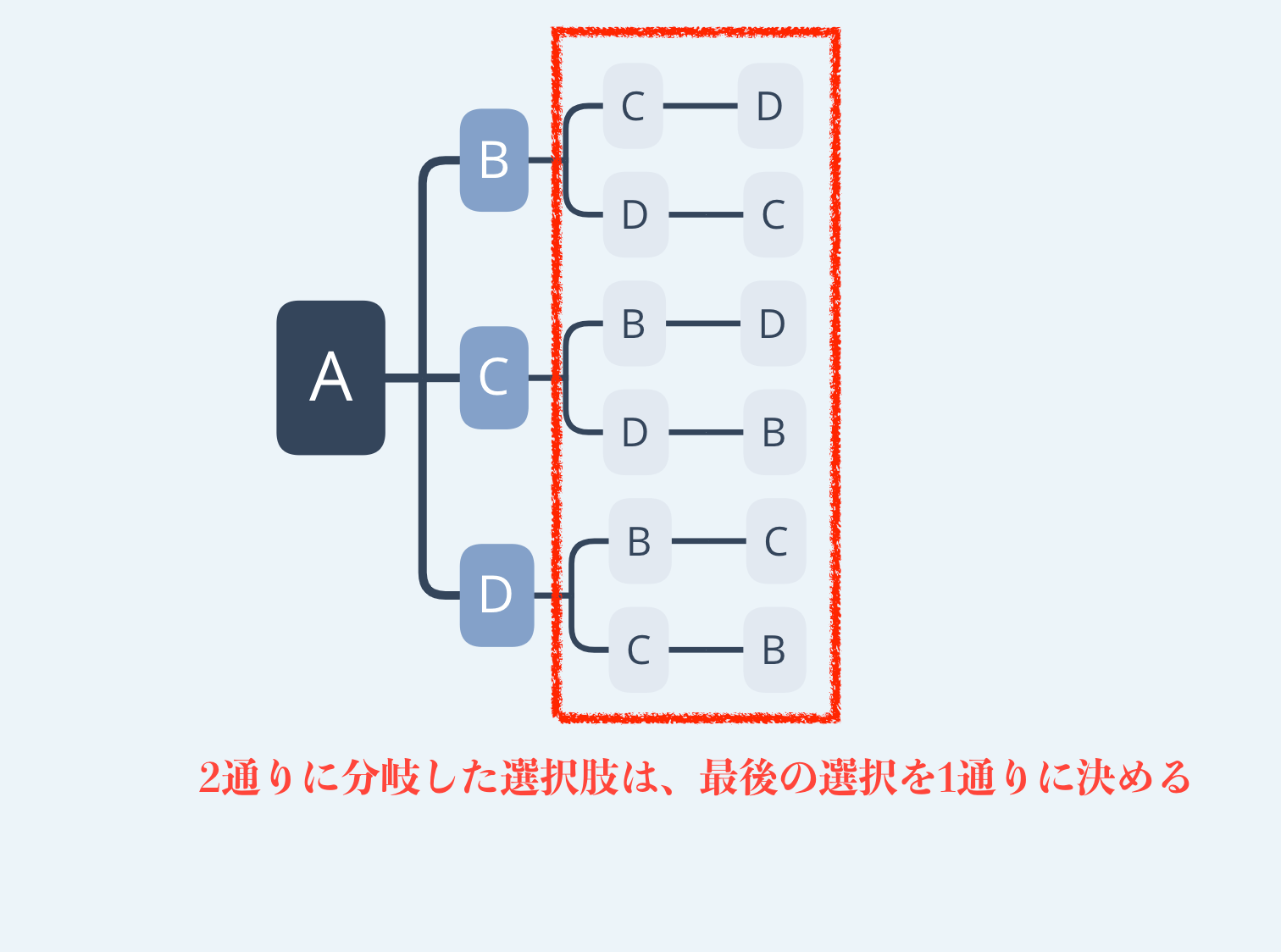


そして先頭の選択肢はA,B,C,Dの4通りありましたね。
これはつまり、合計で\(1\times 2\times 3=6\)通りある選択肢が4つあるということです。
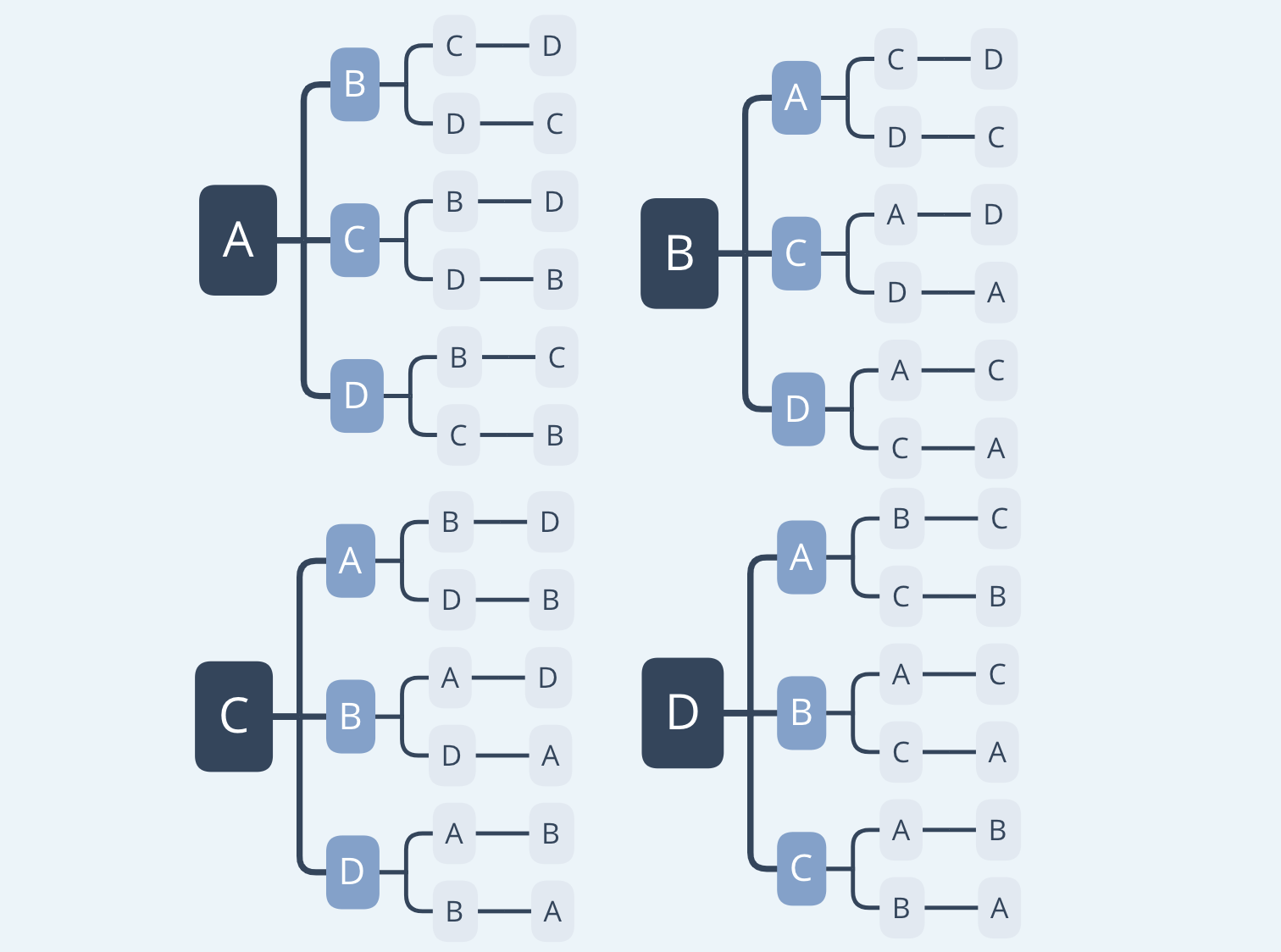
よって、
$$1\times 2\times 3\times 4 = 24通り$$
の選択肢があるということがわかりました。
このように樹形図の枝分かれに着目すると、結果的に分岐した選択肢の個数を掛けていくと全ての場合の数が得られることがわかります。
これを積の法則といいます。
枝分かれの仕方が規則的である場合にのみ使えるものですが、いちいち樹形図を描かなくても計算で全ての場合の数をモレなく、ダブりなく数えることができます。
順列と積の法則の”制限”
例題1のサイコロ問題のように、枝分かれしても選択肢が減らないような樹形図を持つものを『重複(ちょうふく)順列』といい、
例題2の並び方問題のように、枝分かれするたびに選択肢が減るような樹形図を持つものを『順列』といいます。
順列は並び方を考えるときによく登場し、その度に
と書くのはめんどいので、
と表します。
順列は、結局のところ積の法則を満たすようなパターンの『場合の数』をちょっとカッコよく言っただけ。
わからなくなったら、樹形図書けば済む話なんですね。

そして、この積の法則には絶対に忘れてはいけない制限があります。
それは『枝分かれの仕方が均等であること』です。
どれも等しく枝分かれしているからこそ、掛け算ができるのであって、そうでない場合は使えません。


和の法則とはなんだろう。→場合分けして数えてる
ここでは次の例題を考えてみましょう。
例題
5枚のカードがあり、それぞれ0,1,2,3,4と書かれている。このうち3枚のカードを並べて、3桁の偶数を作るパターンは全部で何通りか。
ここでも最初に樹形図を考えますが、”3桁の偶数”を作るので一の位が偶数であればいいですね。
そこで最初に一の位の選択肢から考えていきます。
例えば一の位が0の数を考えると、
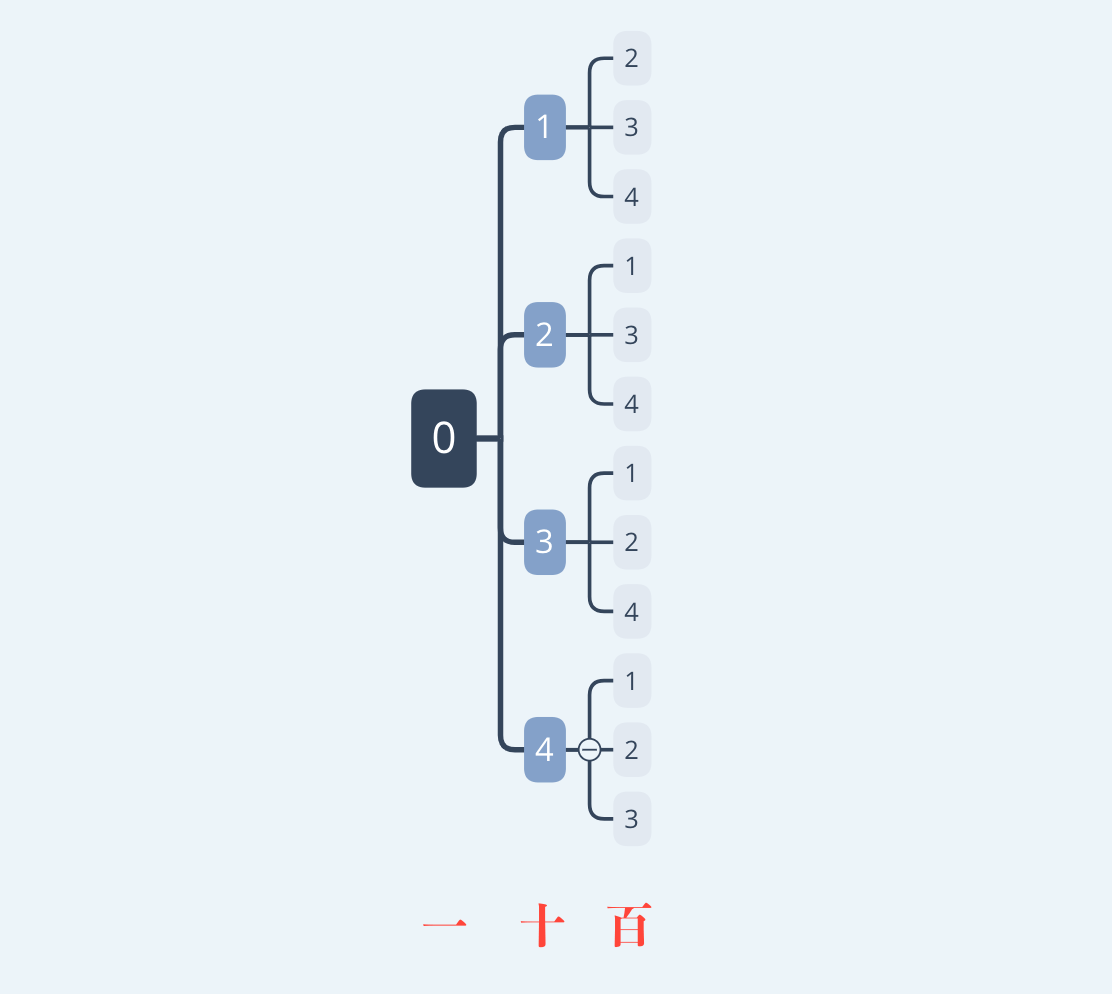


では一の位が2の場合、4の場合はどうでしょうか。
ここで注意してもらいたいのは、百の位に0を選ぶことはできないという点です。すると、
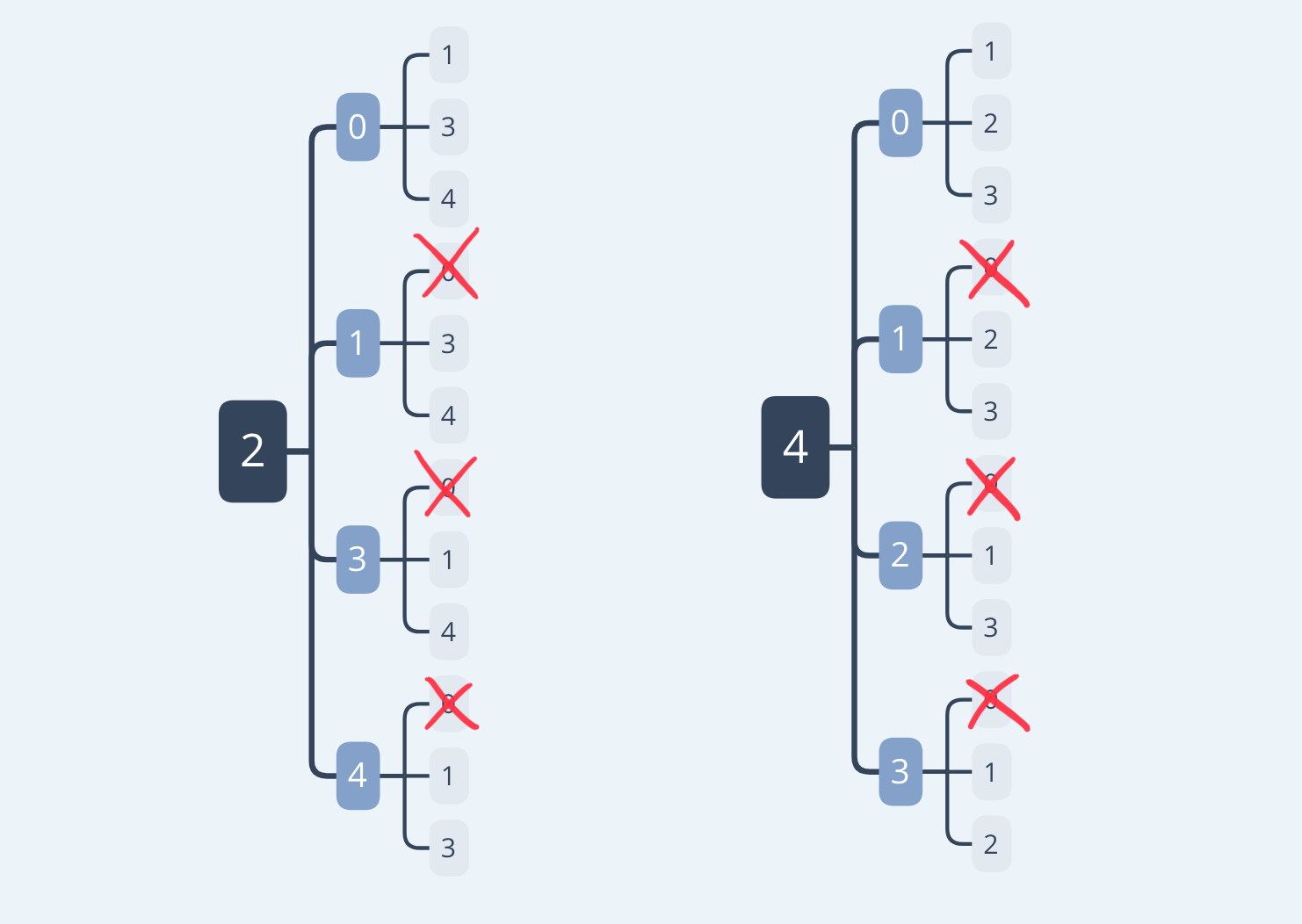


一の位が2のとき、選択肢の合計は(地道に数えてみると)、9通りです。
同様に一の位が4のときも9通りですね。
結論として、3桁の偶数になる場合、
- 一の位が0のとき→12通り
- 一の位が2のとき→9通り
- 一の位が4のとき→9通り
なので、全部合わせて
$$12+9+9=30通り$$
となります。
このように枝分かれが均等でない場合、自分が考えやすい場面で場合分けして、あとで一気に足す方法を和の法則といいます。
まとめ→『モレなく、ダブりなく』を徹底しよう

まとめ
- 場合の数は『モレなく、ダブりなく』数えたいだけ。
- モレなく、ダブりなく数えるために樹形図が有用。ただ樹形図は描くのがめんどいので↓
- 枝分かれが均等なら『積の法則』
- 均等でないなら場合分けして『和の法則』
今回例で扱った問題以外にも、実に多くのパターンの場合の数を考えることができます。
その度に意識してもらいたいのは、『モレなく、ダブりなく』数えたいだけということ。



これから先には円順列や同じもの順列など、いろんなパターンの問題が登場します。
その度にどこに着目し、どんな規則性があるのかを考えてみてください。
以上、「場合の数の意味と和の法則/積の法則の意味」でした。
Q.2つのサイコロを投げた時、サイコロの目の出方は何通りあるか。
$$\ $$
1つ目のサイコロの目の出方は6通り。1つ目のサイコロの目の出方に対して、2つ目のサイコロの目の出方は6通りずつ対応する。
つまり、6通りの出方それぞれに6通りの枝分かれがあるので
$$6\times 6 = 36通り$$
$$\ $$
Q.2つのサイコロを投げた時、サイコロの目の和が5、もしくは6となるのは何通りか。
$$\ $$

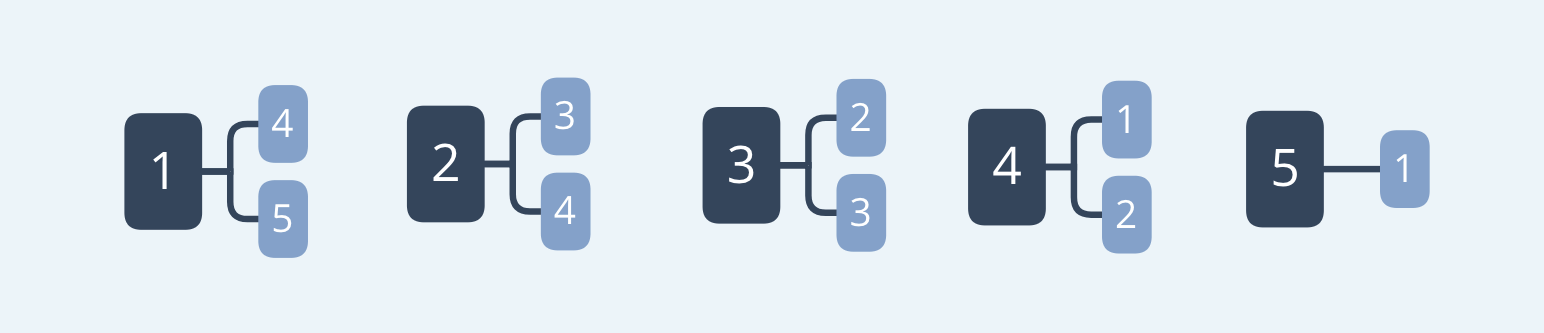
- 【1つ目のサイコロの目が1の時】2通り
- 【1つ目のサイコロの目が2の時】2通り
- 【1つ目のサイコロの目が3の時】2通り
- 【1つ目のサイコロの目が4の時】2通り
- 【1つ目のサイコロの目が5の時】1通り
よって、全部合わせて9通り








