sinの極限と応用公式｜三角関数の極限の不定形はこいつで対処しろ

Today's Topic

$$\lim_{x\rightarrow0}\frac{\sin x}{x}=1$$

小春

楓くん、サインコサインの極限公式がイマイチわからないんだよね。

サインコサインの極限公式は、実は3つのある公式に帰着できるんだ。

楓

小春

どんな問題でも？

そう、どんな問題でも。逆にいえば、ここが抜けているといつまで経っても問題が解けない・・・。

楓

小春

じゃあ今日はその公式と、使い方のポイントを教えて欲しいな！

この記事を読むと、この問題がわかる！

$$\lim_{x\rightarrow0}\frac{\sin3x}{\sin2x}$$
$$\lim_{x\rightarrow0}\frac{2x-x^2}{x+\sin x}$$

楓

最後に解説するよ！

Contents

1 【覚える公式は3つだけ】すべては$\frac{\sin x}{x}$に持ち込める！
2 【証明】$\frac{\sin x}{x}$の極限は、図形的なはさみうち！
3 【他極限への応用】強引に3公式に帰着する
4 まとめ

【覚える公式は3つだけ】すべては$\frac{\sin x}{x}$に持ち込める！

三角関数の極限として覚えるべきは以下の3つです。

楓

三角関数の極限で不定形になったら、大体こいつらの出番！

ポイント

$$\lim_{x\rightarrow 0}\frac{\sin x}{x}=1$$
$$\lim_{x\rightarrow 0}\frac{\tan x}{x}=1$$
$$\lim_{x\rightarrow 0}\frac{1-\cos x}{x^2}=\frac{1}{2}$$

小春

全部$x\rightarrow0$なんだね！

公式2、3は公式1をもとに導くことができるので、自力で導出できるようになっておくと大学入試でも安心して使うことができます。

楓

つまりどんな三角関数の極限も、究極的には公式1まで帰着して考えることができるんだ！

【公式2の証明】
$\frac{\tan x}{x}=\frac{1}{\cos x}\cdot\frac{\sin x}{x}$より、
$$\lim_{x\rightarrow 0}\frac{\tan x}{x}=1\cdot1=1$$

【公式3の証明】
\begin{align} \frac{1-\cos x}{x^2} &= \frac{1-\cos x}{x^2}\cdot\color{red}{\frac{1+\cos x}{1+\cos x}}\\\ &= \left(\frac{\sin x}{x}\right)^2\cdot \frac{1}{\color{red}{1+\cos x}}\\\ \end{align}
よって、
$$\lim_{x\rightarrow 0} \frac{1-\cos x}{x^2} =1^2\cdot\frac{1}{2}=\frac{1}{2}$$

【証明】$\frac{\sin x}{x}$の極限は、図形的なはさみうち！

すべての源になっていた公式1

$$\lim_{x \rightarrow0}\frac{\sin x}{x}=1$$

の証明は、図形的なイメージが重要です。

楓

二等辺△＜扇型＜直角△の関係を利用するよ。

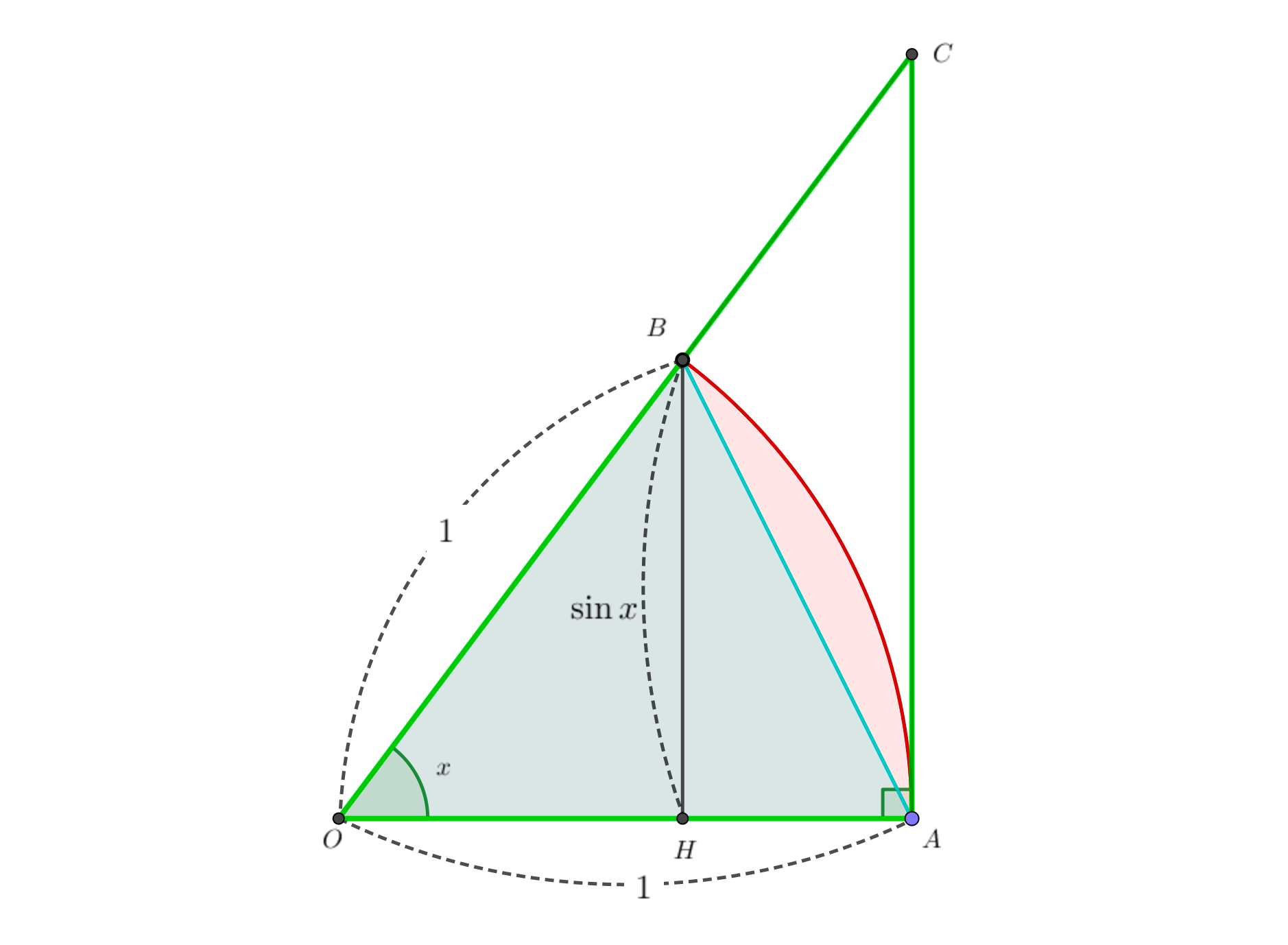
二等辺三角形$\triangle OAB$の面積は$\frac{1}{2}\sin x$
扇型の面積は$\frac{1}{2}x$
直角三角形$\triangle OAC$の面積は$\frac{1}{2}\tan x$

参考

サインコサインの定義から、$BH=\sin x,OH=\cos x$。

比例式$OH:BH=OA:CA$より、

$CA=\frac{BH}{OH}=\frac{\sin x}{\cos x}=\tan x$。

図形の大小関係から、

$\frac{1}{2}\sin x< \frac{1}{2} x < \frac{1}{2}\tan x$

$\frac{1}{2}$を消して逆数の大小関係に着目すると、

$\frac{1}{\tan x} < \frac{1}{x} < \frac{1}{\sin x}$

全辺に$\sin x$をかけると、$\frac{\sin x}{\tan x} < \frac{\sin x}{x} < 1$

$$\frac{\sin x}{\tan x}=\cos x \xrightarrow[x\rightarrow 0]{} 1$$
$$1 \xrightarrow[x\rightarrow 0]{} 1$$

より、はさみうちの原理から、

$$\frac{\sin x}{x} \xrightarrow[x\rightarrow 0]{} 1$$

【他極限への応用】強引に3公式に帰着する

三角関数の場合、どんなどんな極限も大体は３公式に帰着させることができます。

具体的な例題を見てみましょう。

例題

$$\lim_{x\rightarrow0}\frac{\sin 3x}{\sin 2x}$$の値を求めよ。

三角関数の極限で一番厄介なところは、サインコサインのグラフが振動を繰り返しているので、不定形になりやすいという点です。

実際、この例題もそのまま極限を求めると、

$$\frac{\sin 3x}{\sin 2x}\xrightarrow[x\rightarrow0]{}\frac{0}{0}$$

となってしまいます。

不定形にならないようにするために、先ほどの3公式に帰着するとうまくいく場合が多いです。

$x\rightarrow0$とはすなわち$x\neq0$を仮定しているので、

\begin{align} \frac{\sin 3x}{\sin 2x} &= \frac{\frac{\sin 3x}{\color{blue}{3x}}\cdot\color{blue}{3x}}{\frac{\sin 2x}{\color{red}{2x}}\cdot\color{red}{2x}}\\\ &\xrightarrow[x\rightarrow0]{} \frac{3}{2}\\\ \end{align}

となります。

楓

無理やり$\frac{\sin ●}{●}$の形を作り出すんだね。

もう1つみてみましょう。

例題

$$\lim_{x\rightarrow\frac{\pi}{2}}\frac{\cos x}{\frac{\pi}{2}-x}$$

この手の極限を見たときに、最初にこう思う人がいます。

$x\rightarrow\frac{\pi}{2}$だから、$x\rightarrow0$の3公式は使えないなぁ。

違います。

使えるように変形しようとすることが大事なのです。

この式もこのまま極限を求めようとすると$\frac{0}{0}$不定形になってしまいます。

そこで、

$$y=\frac{\pi}{2}-x$$

と置いてみたらどうでしょうか。

$x\rightarrow\frac{\pi}{2}$であれば、$y\rightarrow0$となり公式が使える形のスタートラインまでは持っていけます。

与えられた式を$x$の式から、$y$の式に変形させていきましょう。

$y=\frac{\pi}{2}-x$なので、$x=\frac{\pi}{2}-y$に置き換えてあげましょう。

\begin{align} \frac{\cos x}{\frac{\pi}{2}-x} &= \frac{\cos \left(\frac{\pi}{2}-y\right)}{y}\\\ &= \frac{\sin y}{y}\\\ \end{align}

楓

コサインの変換公式でサインに変化したね。

最後の形はおなじみですね？

$$\lim_{y\rightarrow0}\frac{\sin y}{y}=1$$

となりました。

まとめ

楓

お疲れ！まとめ！

まとめ

三角関数の極限は、

$$\lim_{x\rightarrow 0}\frac{\sin x}{x}=1$$
$$\lim_{x\rightarrow 0}\frac{\tan x}{x}=1$$
$$\lim_{x\rightarrow 0}\frac{1-\cos x}{x^2}=\frac{1}{2}$$

の3つのどれかに帰着させて考えれば良い。

公式2、3は公式1に帰着でき、公式1は二等辺△＜扇型＜直角△の関係から証明すれば良い。

三角関数の極限は、慣れてしまえばそれほど難しくありません。

当然この公式だけですべての極限が求められるようになるわけではありません。

が、高校数学で出題される範囲ではこの３公式が圧倒的に強いので、完璧にしておきましょう。

チェック問題

例題

$$\lim_{x\rightarrow0}\frac{2x-x^2}{x+\sin x}$$

（解答）

$$\lim_{x\rightarrow0}\frac{2x-x^2}{x+\sin x}$$

そのまま求めると、$\frac{0}{0}$不定形になってしまう。

そこで、分母分子を$x$で割ってみると、

\begin{align} \frac{2x-x^2}{x+\sin x} &= \frac{\frac{2x-x^2}{\color{red}{x}}}{\frac{x+\sin x}{\color{red}{x}}}\\\ &= \frac{2-x}{1+\frac{\sin x}{x}}\\\ \end{align}

となる。

よって、

$$\frac{2-x}{1+\frac{\sin x}{x}} \xrightarrow[x\rightarrow0]{} \frac{2}{1+1}=1$$