Today's Topic
\(n\)個の要素を並べた円順列の場合の数は$$(n-1)!通り$$





こんなあなたへ
「円順列を考える意味がわからない。何のために円形に並べるの?!」
「円順列の公式の意味がわからない。何がしたいの?」
この記事を読むと、この意味がわかる!
- AからFまでの6人を円形に並べたとき、輪の作り方は何通り?
- AからFまでの6人を円形に並べたとき、AとFが向かい合わせになるのは何通り?

Contents
順列とは何か→横並びにしたときの場合の数を求めたい

順列とは、異なるものを順番に並べる方法のことを言います。具体的に次の例題を見てみましょう。
例題
赤、青、緑、白、黒の5色の玉が1つずつある。これを一列に並べたとき、並べ方は何通りあるか。
例えば1番目に赤色の玉を置いたとすると、樹形図はこのようになります。
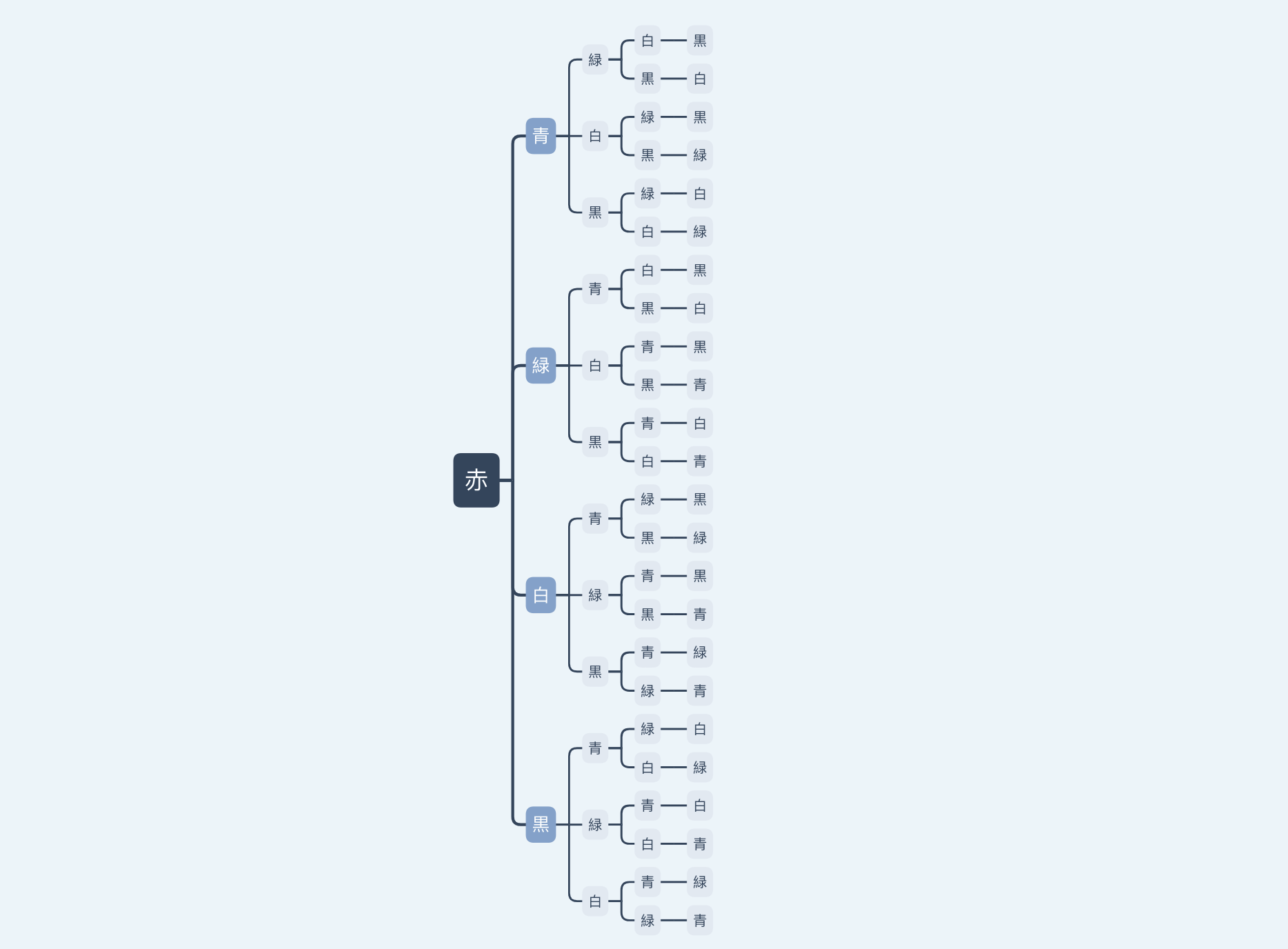
枝が均等に分かれているので、積の法則が使えそうです。
和の法則・積の法則について復習したい人はこちらを参考にしてください。
続きを見る

場合の数ができない人は、ここが抜けてる!しっかり数えるための和の法則・積の法則→モレなく、ダブりなく
枝の分かれ方に着目すると、1番目に赤色を選択した場合、
の選択肢があります。
そして1番目の選択肢は赤から黒までの5通りなので、
の選択肢がありそうです。


順列ではこのように、1つずつ値が減っていき、それらを順に掛ける計算が非常に多く出てきます。
そこで、
のように「!」をつけることで1まで掛け算し続けるということを表します。
円順列とは何か→円形に並べたときの場合の数を求めたい


さて、本題に入りましょう。
円順列とは、先ほど一列に並べた玉を円形に並べたときの並べる方法のことです。

はい、これだけです。








円順列の前提条件と重要な”制限”
順列と円順列は、一列に並べているか、円形に並べているかの違いしかありません。
しかしこの、円形という並びが場合の数を考える上で超大事なポイントになります。
では具体的にみていきましょう。
まずは2つの順列を見比べてみましょう。
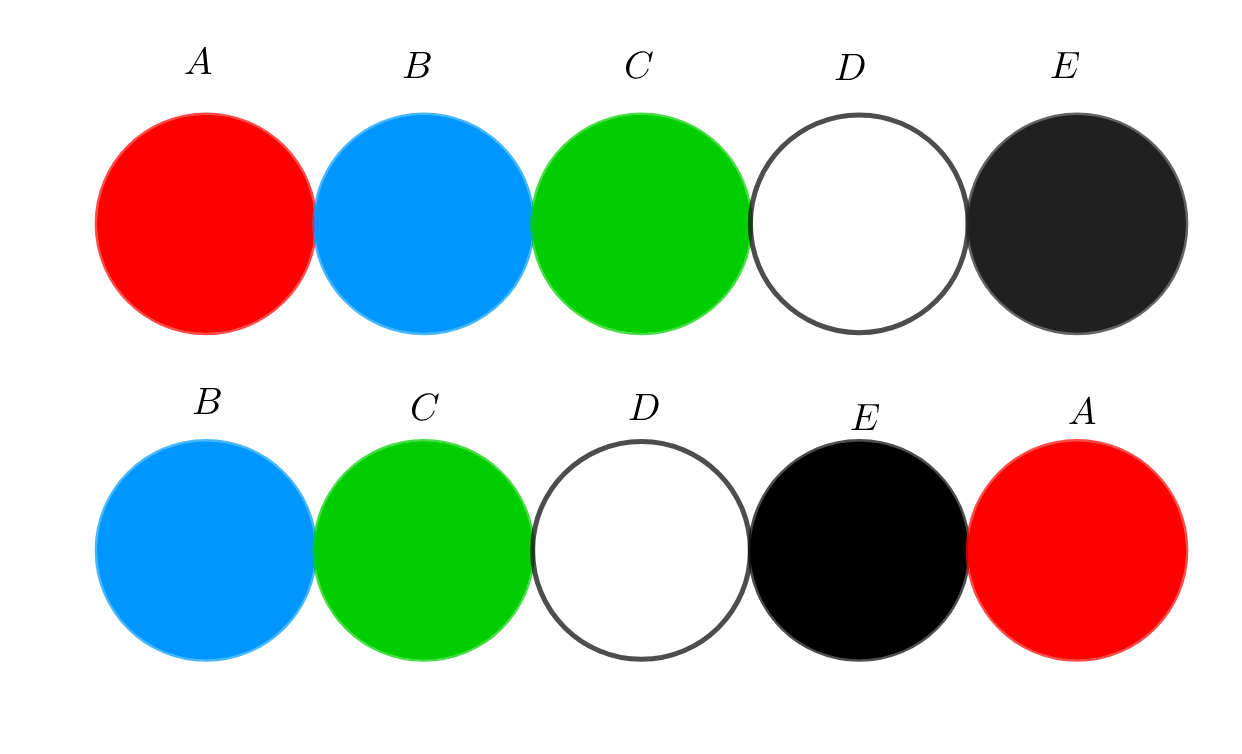





一列に並べると、どれか1つの玉を動かしただけでも並び方が全く違うものになりますね。
では、円形の場合はどうでしょうか。
次の2つを見比べてみましょう。
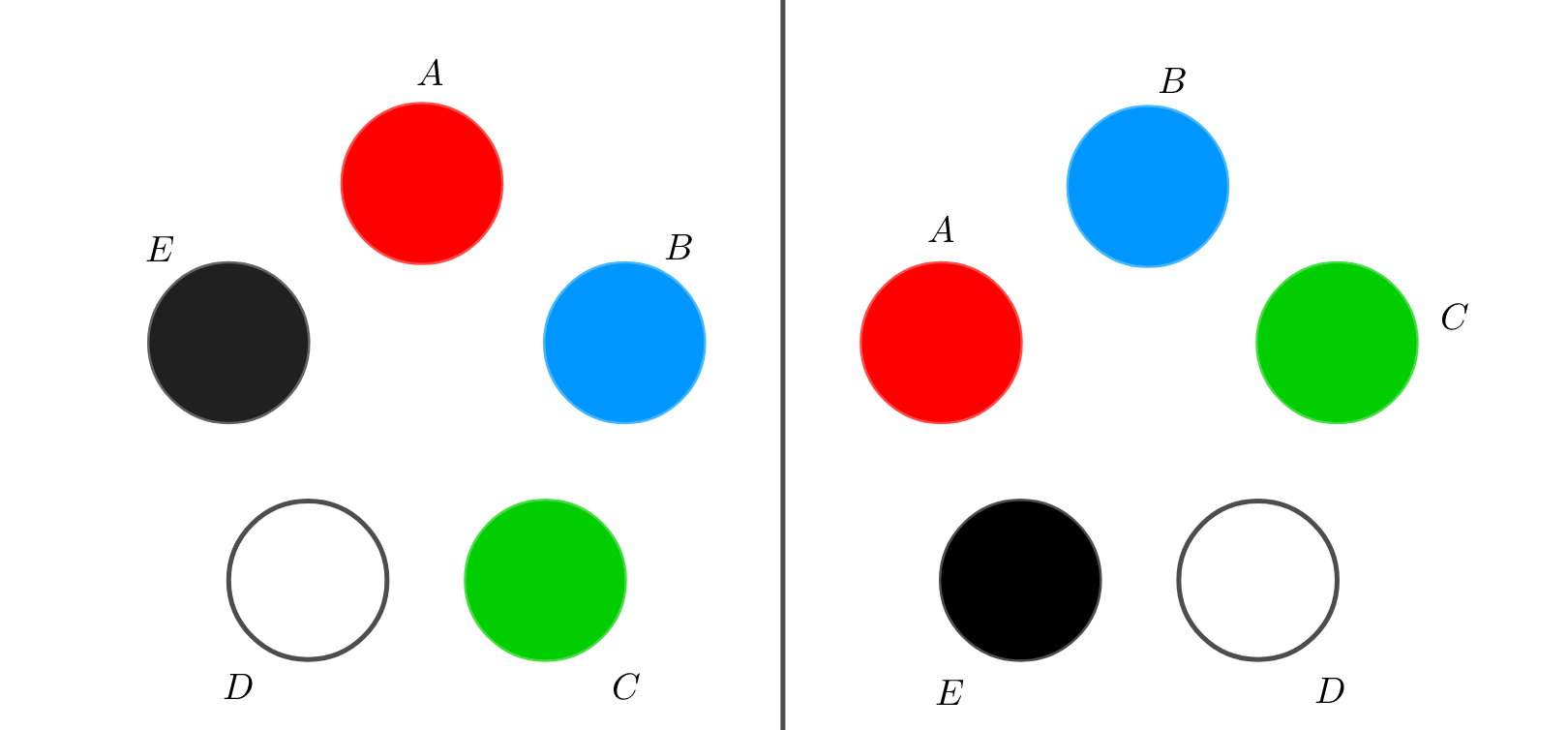



では次のように見てみるとどうでしょうか。


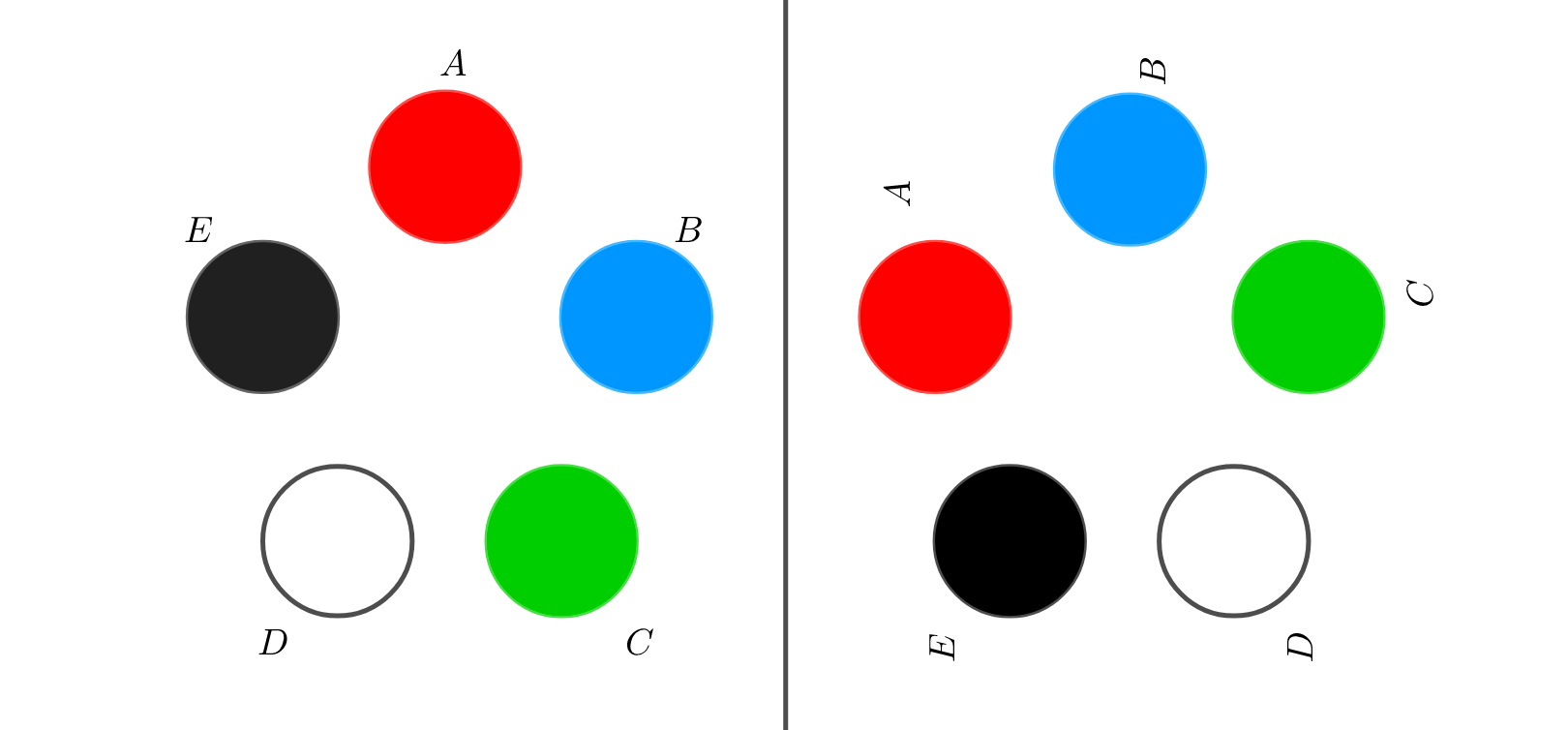





このように円順列では、
みる角度を変えただけで同じになる並び方は、全て同じとみなす
という特殊な前提条件があります。


今回のケースだと、以下5つの並び方はすべて同じ並びとみなされます。
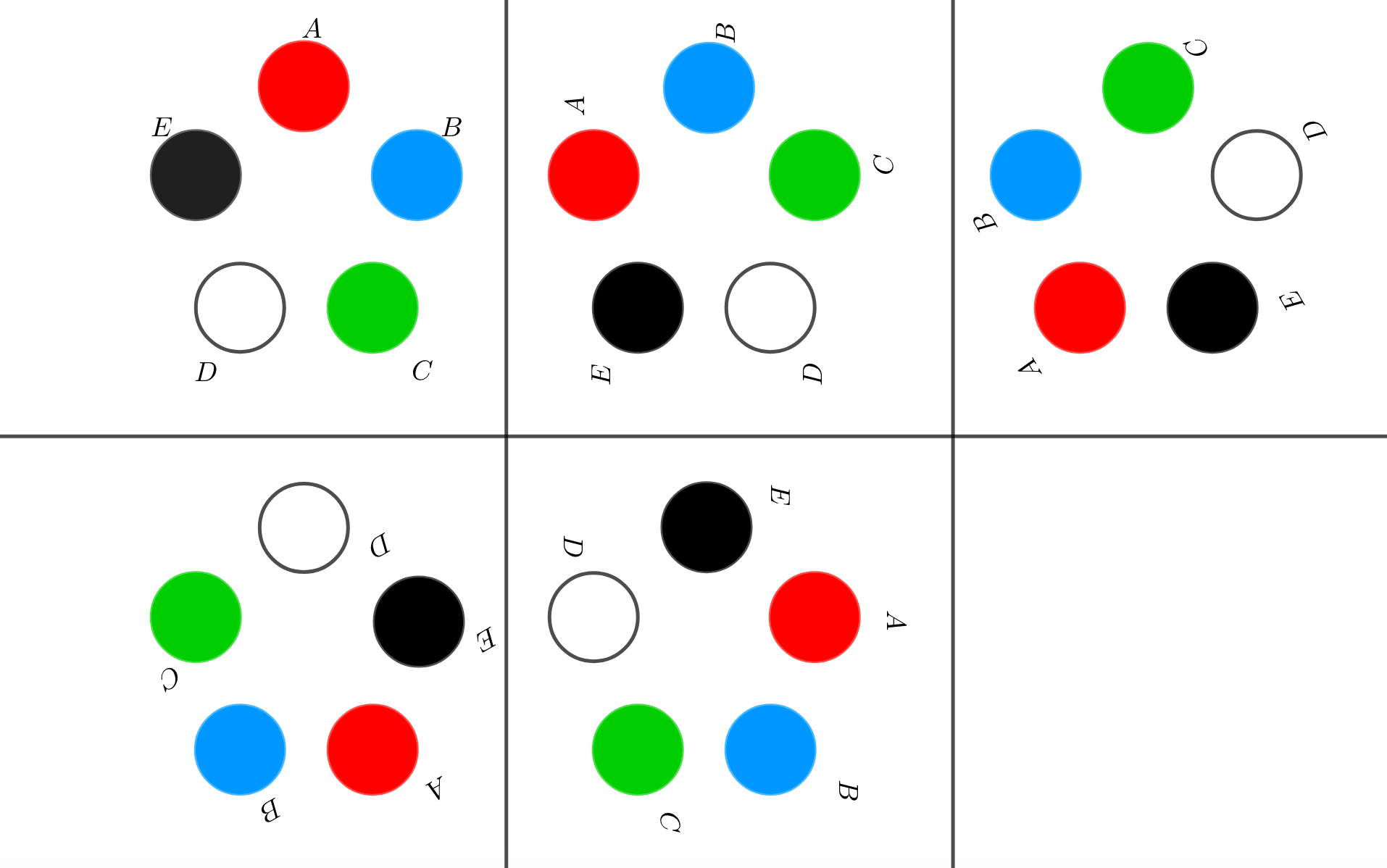

ここまでの内容をまとめてみると、円順列は円形に並べたことによって
- 一見違うように見えても、回転すると同じとみなせる並び方があった。
- そこでみる角度を変えると同じ並びになるパターンは全て、同じものとみなすことにした。
というわけです。
円順列の場合の数の求め方→ダブっているパターンを取り除く


円順列は、一列に並べる順列とは違い、みる角度を変えて同じ並びになるパターンは同じものとみなすという特殊な性質があります。
これはつまり、普通に数えると『ダブり』が発生してしまうことを意味します。
例えば、一列に並べる順列の場合、


上図のような並び方は、異なるパターンとみなされ2通りとカウントされます。
一方、円順列の場合、


は全く同じものとみなすので、これを2通りとすると、ダブって数えていることになってしまいます。


つまり円順列では、同じとみなせる並び方を数えないようにする工夫が必要になるわけです。
ではこの問題となっている、『同じとみなせる並び方』はいくつあるのでしょうか。
今回の例で言えば、すでにご紹介した通り、以下5つの並び方は同じものとみなされます。


この図を見てわかるのは、
反時計回りにちょうど一周するまでに作られるパターンは、全て最初の並び方と同じ並び方と考える
ということ。


これを『5通り』とカウントすると、ダブってカウントしていることになるので、
とすることで、しっかりカウントすることができます。
玉の並び方自体は、一列に並べた順列と同じ
通りだけ存在します。
しかしこれは、同じ玉の並べ方を『5通り』とダブっているにもかかわらずカウントした場合の数です。
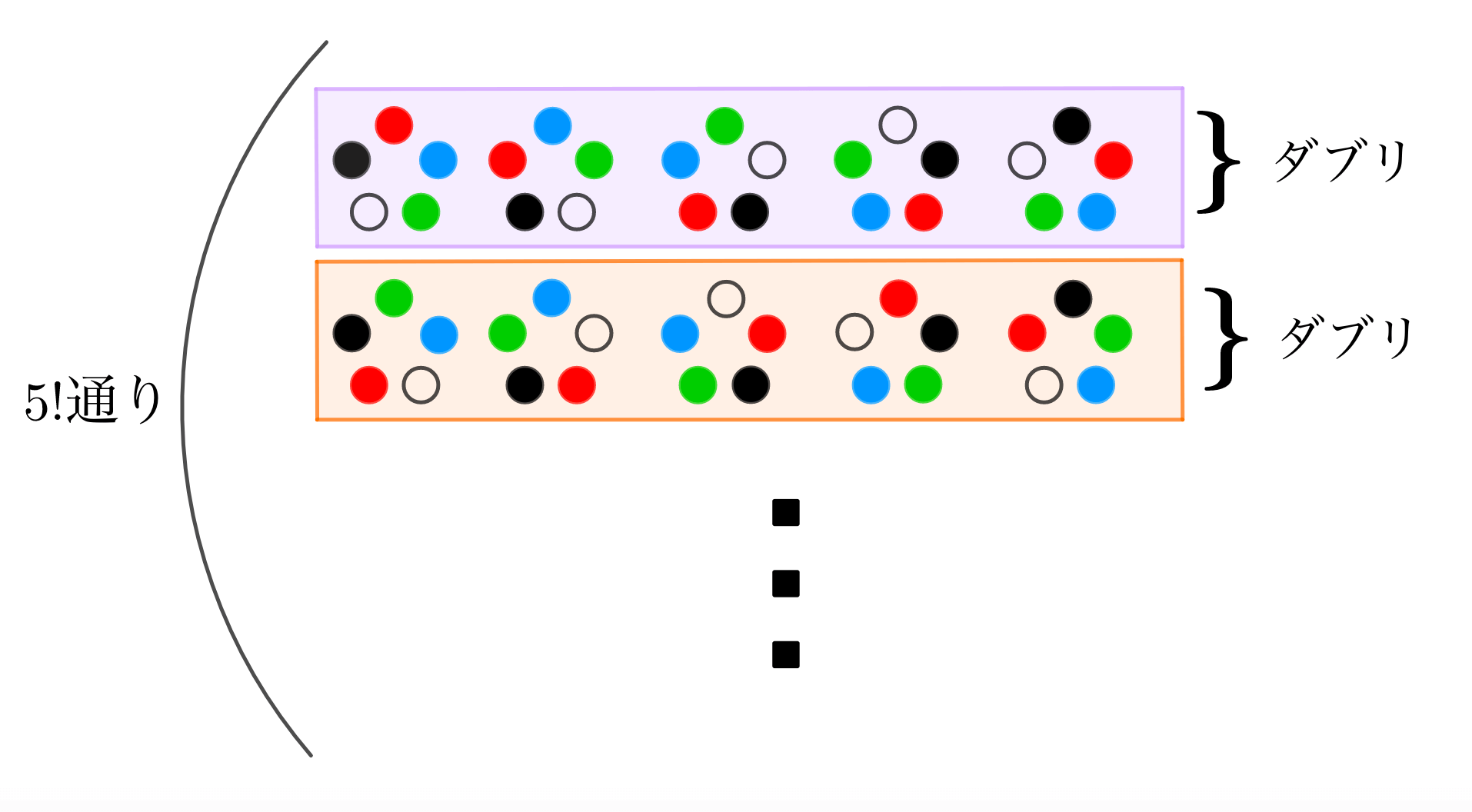

そこでダブりを解消するために、
とすることで、正しくカウントします。


今回の場合、
となります。
\(n\)個の要素を並べてできる円順列は、基本的に\((n-1)!\)で求められますが、この公式よりも考え方を重視して欲しいです。
ポイント
円順列でしっかり場合の数をカウントするためには、
$$並び方の総数 \div ダブっているパターン数$$
を考えれば良い。
円順列をやる意味→ダブっているときを考える練習
最後に、なんでわざわざ円形に並べるなんていう場合の数を求めなきゃいけないのでしょうか。


結論を言うと、円順列の問題の答えを求めることにあまり価値はないと思っています。
円順列を扱う本当の意味は、今回何度も言っている『ダブリ』の解消について考えるため、と僕は解釈しています。
これから先、色々な場合の数が出てきますが、結局何通りあるかをモレなくダブリなく数えたいだけです。
ダブりの規則性がわかっていれば、今回のようにサッと計算で求めることができます。




まとめ


まとめ
- 円順列は、一列に並べた順列とは異なり、回転すると同じ並び方とみなせるという条件がある。
- この条件により、普通に数えるとダブりが発生してしまう。
- そこで、ダブリが均等であることに着目し、$$並び方の総数 \div ダブっているパターン数$$を考えれば良い。
円順列はこれから先の場合の数で出てくる『ダブリ』解消の大きなヒントを与えてくれます。
ぜひ円順列で、ダブリをしないための計算を身につけてください。
以上、「円順列とは何か」でした。
Q.AからFまでの6人を円形に並べたとき、輪の作り方は何通り?
$$\ $$
並べ方自体は\(6!\)通り。
ただし円順列特有の『回転して同じ並びは同じもの』という性質により、ダブリが発生する。
このダブりは、どの並びでも均等に6パターンできる。
$$\ $$
よって、\(\frac{6!}{6}=120通り\)
$$ \ $$
Q.AからFまでの6人を円形に並べたとき、AとFが向かい合わせになるのは何通り?
図のようにAとFの位置を固定すると、回転しないので『ダブリ』が発生しない。
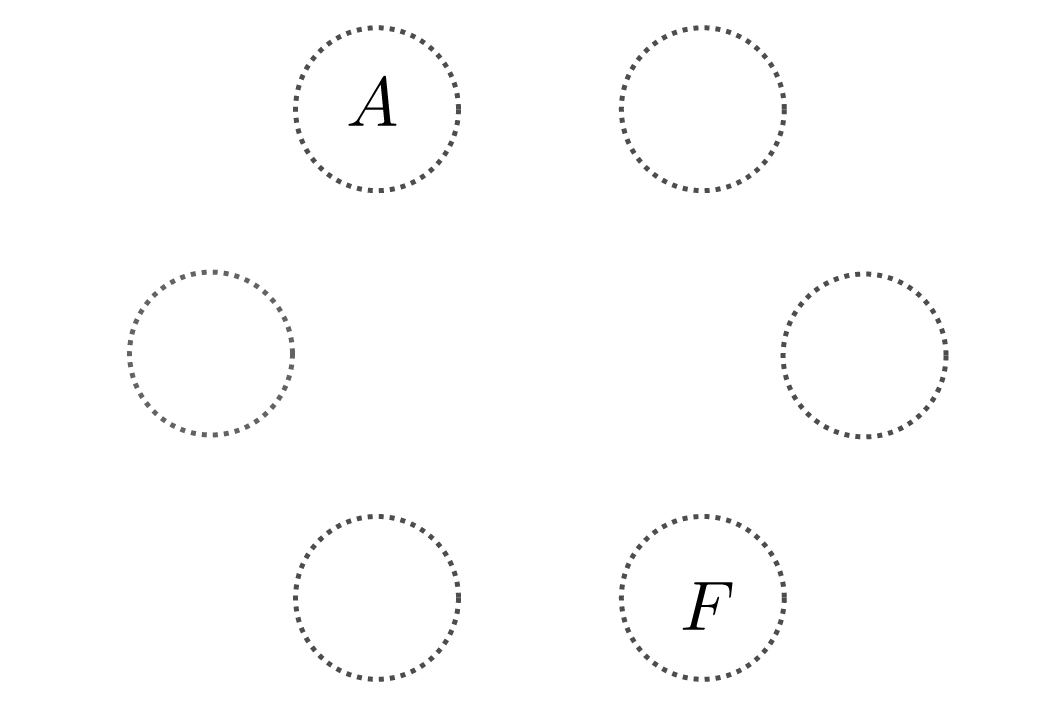

よって、残り4箇所の並び方を考えればいいので、
$$4! =24通り$$








